【機(jī)器學(xué)習(xí)】機(jī)器學(xué)習(xí)算法之——K最近鄰(k-Nearest Neighbor，KNN)分類算法原理講解
k-最近鄰算法是基于實(shí)例的學(xué)習(xí)方法中最基本的，先介紹基于實(shí)例學(xué)習(xí)的相關(guān)概念。
01
基于實(shí)例的學(xué)習(xí)
已知一系列的訓(xùn)練樣例，很多學(xué)習(xí)方法為目標(biāo)函數(shù)建立起明確的一般化描述；但與此不同，基于實(shí)例的學(xué)習(xí)方法只是簡(jiǎn)單地把訓(xùn)練樣例存儲(chǔ)起來(lái)。
從這些實(shí)例中泛化的工作被推遲到必須分類新的實(shí)例時(shí)。每當(dāng)學(xué)習(xí)器遇到一個(gè)新的查詢實(shí)例，它分析這個(gè)新實(shí)例與以前存儲(chǔ)的實(shí)例的關(guān)系，并據(jù)此把一個(gè)目標(biāo)函數(shù)值賦給新實(shí)例。
基于實(shí)例的方法可以為不同的待分類查詢實(shí)例建立不同的目標(biāo)函數(shù)逼近。事實(shí)上，很多技術(shù)只建立目標(biāo)函數(shù)的局部逼近，將其應(yīng)用于與新查詢實(shí)例鄰近的實(shí)例，而從 不建立在整個(gè)實(shí)例空間上都表現(xiàn)良好的逼近。當(dāng)目標(biāo)函數(shù)很復(fù)雜，但它可用不太復(fù)雜的局部逼近描述時(shí)，這樣做有顯著的優(yōu)勢(shì)。
基于實(shí)例方法的不足
分類新實(shí)例的開銷可能很大。這是因?yàn)閹缀跛械挠?jì)算都發(fā)生在分類時(shí)，而不是在第一次遇到訓(xùn)練樣例時(shí)。所以，如何有效地索引訓(xùn)練樣例，以減少查詢時(shí)所需計(jì)算是一個(gè)重要的實(shí)踐問題。
當(dāng)從存儲(chǔ)器中檢索相似的訓(xùn)練樣例時(shí)，它們一般考慮實(shí)例的所有屬性。如果目標(biāo)概念僅依賴于很多屬性中的幾個(gè)時(shí)，那么真正最“相似”的實(shí)例之間很可能相距甚遠(yuǎn)。
02
k-最近鄰算法
1. 算法概述
鄰近算法，或者說(shuō)K最近鄰(K-Nearest Neighbor,KNN)分類算法是數(shù)據(jù)挖掘分類技術(shù)中最簡(jiǎn)單的方法之一，是著名的模式識(shí)別統(tǒng)計(jì)學(xué)方法，在機(jī)器學(xué)習(xí)分類算法中占有相當(dāng)大的地位。它是一個(gè)理論上比較成熟的方法。既是最簡(jiǎn)單的機(jī)器學(xué)習(xí)算法之一，也是基于實(shí)例的學(xué)習(xí)方法中最基本的，又是最好的文本分類算法之一。
所謂K最近鄰，就是k個(gè)最近的鄰居的意思，說(shuō)的是每個(gè)樣本都可以用它最接近的k個(gè)鄰居來(lái)代表。Cover和Hart在1968年提出了最初的鄰近算法。KNN是一種分類(classification)算法，它輸入基于實(shí)例的學(xué)習(xí)（instance-based learning），屬于懶惰學(xué)習(xí)（lazy learning）即KNN沒有顯式的學(xué)習(xí)過(guò)程，也就是說(shuō)沒有訓(xùn)練階段，數(shù)據(jù)集事先已有了分類和特征值，待收到新樣本后直接進(jìn)行處理。與急切學(xué)習(xí)（eager learning）相對(duì)應(yīng)。
2. 算法思想
KNN是通過(guò)測(cè)量不同特征值之間的距離進(jìn)行分類。
思路是：如果一個(gè)樣本在特征空間中的k個(gè)最鄰近的樣本中的大多數(shù)屬于某一個(gè)類別，則該樣本也劃分為這個(gè)類別。 KNN算法中，所選擇的鄰居都是已經(jīng)正確分類的對(duì)象。該方法在定類決策上只依據(jù)最鄰近的一個(gè)或者幾個(gè)樣本的類別來(lái)決定待分樣本所屬的類別。
該算法假定所有的實(shí)例對(duì)應(yīng)于N維歐式空間?n中的點(diǎn)。通過(guò)計(jì)算一個(gè)點(diǎn)與其他所有點(diǎn)之間的距離，取出與該點(diǎn)最近的K個(gè)點(diǎn)，然后統(tǒng)計(jì)這K個(gè)點(diǎn)里面所屬分類比例最大的，則這個(gè)點(diǎn)屬于該分類。
該算法涉及3個(gè)主要因素：實(shí)例集、距離或相似的衡量、k的大小。
一個(gè)實(shí)例的最近鄰是根據(jù)標(biāo)準(zhǔn)歐氏距離定義的。更精確地講，把任意的實(shí)例x表示為下面的特征向量：
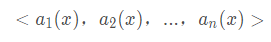
其中ar(x)表示實(shí)例x的第r個(gè)屬性值。那么兩個(gè)實(shí)例xi和xj間的距離定義為d(xi,xj)，其中：
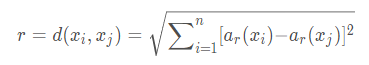
3. 有關(guān)KNN算法的幾點(diǎn)說(shuō)明
在最近鄰學(xué)習(xí)中，目標(biāo)函數(shù)值可以為離散值也可以為實(shí)值。
我們先考慮學(xué)習(xí)以下形式的離散目標(biāo)函數(shù)。其中V是有限集合{v1,…,vs}。下表給出了逼近離散目標(biāo)函數(shù)的k-近鄰算法。
正如下表中所指出的，這個(gè)算法的返回值f′(xq)為對(duì)f(xq)的估計(jì)，它就是距離xq最近的k個(gè)訓(xùn)練樣例中最普遍的f值。
如果我們選擇k=1，那么“1-近鄰算法”就把f(xi)賦給(xq)，其中xi是最靠近xq的訓(xùn)練實(shí)例。對(duì)于較大的k值，這個(gè)算法返回前k個(gè)最靠近的訓(xùn)練實(shí)例中最普遍的f值。
逼近離散值函數(shù)f:?n?V的k-近鄰算法
訓(xùn)練算法：
??對(duì)于每個(gè)訓(xùn)練樣例<x,f(x)>，把這個(gè)樣例加入列表training_examples分類算法：
??給定一個(gè)要分類的查詢實(shí)例xq 在training_examples中選出最靠近xq的k個(gè)實(shí)例，并用x1,…,xk表示返回
其中如果a=b那么d(a,b)=1，否則d(a,b)=0
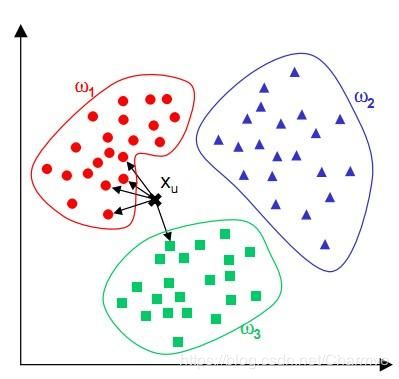
簡(jiǎn)單來(lái)說(shuō)，KNN可以看成：有那么一堆你已經(jīng)知道分類的數(shù)據(jù)，然后當(dāng)一個(gè)新數(shù)據(jù)進(jìn)入的時(shí)候，就開始跟訓(xùn)練數(shù)據(jù)里的每個(gè)點(diǎn)求距離，然后挑離這個(gè)訓(xùn)練數(shù)據(jù)最近的K個(gè)點(diǎn)看看這幾個(gè)點(diǎn)屬于什么類型，然后用少數(shù)服從多數(shù)的原則，給新數(shù)據(jù)歸類。
4. KNN算法的決策過(guò)程
下圖中有兩種類型的樣本數(shù)據(jù)，一類是藍(lán)色的正方形，另一類是紅色的三角形，中間那個(gè)綠色的圓形是待分類數(shù)據(jù)：
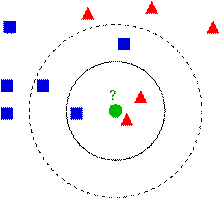
如果K=3，那么離綠色點(diǎn)最近的有2個(gè)紅色的三角形和1個(gè)藍(lán)色的正方形，這三個(gè)點(diǎn)進(jìn)行投票，于是綠色的待分類點(diǎn)就屬于紅色的三角形。而如果K=5，那么離綠色點(diǎn)最近的有2個(gè)紅色的三角形和3個(gè)藍(lán)色的正方形，這五個(gè)點(diǎn)進(jìn)行投票，于是綠色的待分類點(diǎn)就屬于藍(lán)色的正方形。
下圖則圖解了一種簡(jiǎn)單情況下的k-最近鄰算法，在這里實(shí)例是二維空間中的點(diǎn)，目標(biāo)函數(shù)具有布爾值。正反訓(xùn)練樣例用“+”和“-”分別表示。圖中也畫出了一個(gè)查詢點(diǎn)xq。注意在這幅圖中，1-近鄰算法把xq分類為正例，然而5-近鄰算法把xq分類為反例。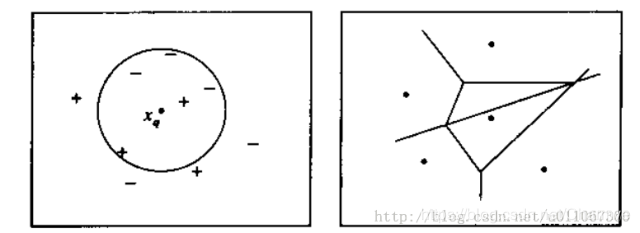
圖解說(shuō)明： 左圖畫出了一系列的正反訓(xùn)練樣例和一個(gè)要分類的查詢實(shí)例xq。1-近鄰算法把xq分類為正例，然而5-近鄰算法把xq分類為反例。
右圖是對(duì)于一個(gè)典型的訓(xùn)練樣例集合1-近鄰算法導(dǎo)致的決策面。圍繞每個(gè)訓(xùn)練樣例的凸多邊形表示最靠近這個(gè)點(diǎn)的實(shí)例空間（即這個(gè)空間中的實(shí)例會(huì)被1-近鄰算法賦予該訓(xùn)練樣例所屬的分類）。
對(duì)前面的k-近鄰算法作簡(jiǎn)單的修改后，它就可被用于逼近連續(xù)值的目標(biāo)函數(shù)。為了實(shí)現(xiàn)這一點(diǎn)，我們讓算法計(jì)算k個(gè)最接近樣例的平均值，而不是計(jì)算其中的最普遍的值。更精確地講，為了逼近一個(gè)實(shí)值目標(biāo)函數(shù)f:Rn?R，我們只要把算法中的公式替換為：
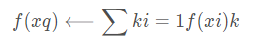
03
針對(duì)傳統(tǒng)KNN算法的改進(jìn)
1. 快速KNN算法。參考FKNN論述文獻(xiàn)（實(shí)際應(yīng)用中結(jié)合lucene）
2. 加權(quán)歐氏距離公式。在傳統(tǒng)的歐氏距離中,各特征的權(quán)重相同,也就是認(rèn)定各個(gè)特征對(duì)于分類的貢獻(xiàn)是相同的,顯然這是不符合實(shí)際情況的。同等的權(quán)重使得特征向量之間相似度計(jì)算不夠準(zhǔn)確, 進(jìn)而影響分類精度。加權(quán)歐氏距離公式,特征權(quán)重通過(guò)靈敏度方法獲得（根據(jù)業(yè)務(wù)需求調(diào)整，例如關(guān)鍵字加權(quán)、詞性加權(quán)等）
距離加權(quán)最近鄰算法
對(duì)k-最近鄰算法的一個(gè)顯而易見的改進(jìn)是對(duì)k個(gè)近鄰的貢獻(xiàn)加權(quán)，根據(jù)它們相對(duì)查詢點(diǎn)xq的距離，將較大的權(quán)值賦給較近的近鄰。
例如，在上表逼近離散目標(biāo)函數(shù)的算法中，我們可以根據(jù)每個(gè)近鄰與xq的距離平方的倒數(shù)加權(quán)這個(gè)近鄰的“選舉權(quán)”。
方法是通過(guò)用下式取代上表算法中的公式來(lái)實(shí)現(xiàn)：
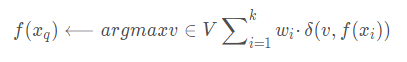
其中，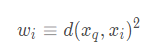
我們也可以用類似的方式對(duì)實(shí)值目標(biāo)函數(shù)進(jìn)行距離加權(quán)，只要用下式替換上表的公式：
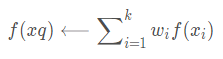
其中，wi的定義與之前公式中相同。
注意這個(gè)公式中的分母是一個(gè)常量，它將不同權(quán)值的貢獻(xiàn)歸一化（例如，它保證如果對(duì)所有的訓(xùn)練樣例xi，f(xi)=c，那么(xq)←c)。
注意以上k-近鄰算法的所有變體都只考慮k個(gè)近鄰以分類查詢點(diǎn)。如果使用按距離加權(quán)，那么允許所有的訓(xùn)練樣例影響xq的分類事實(shí)上沒有壞處，因?yàn)榉浅＿h(yuǎn)的實(shí)例對(duì)(xq)的影響很小。考慮所有樣例的惟一不足是會(huì)使分類運(yùn)行得更慢。如果分類一個(gè)新的查詢實(shí)例時(shí)考慮所有的訓(xùn)練樣例，我們稱此為全局（global）法。如果僅考慮最靠近的訓(xùn)練樣例，我們稱此為局部（local）法。
04
幾個(gè)問題的解答
按距離加權(quán)的k-近鄰算法是一種非常有效的歸納推理方法。它對(duì)訓(xùn)練數(shù)據(jù)中的噪聲有很好的魯棒性，而且當(dāng)給定足夠大的訓(xùn)練集合時(shí)它也非常有效。注意通過(guò)取k個(gè)近鄰的加權(quán)平均，可以消除孤立的噪聲樣例的影響。
1. 問題一： 近鄰間的距離會(huì)被大量的不相關(guān)屬性所支配。
應(yīng)用k-近鄰算法的一個(gè)實(shí)踐問題是，實(shí)例間的距離是根據(jù)實(shí)例的所有屬性（也就是包含實(shí)例的歐氏空間的所有坐標(biāo)軸）計(jì)算的。這與那些只選擇全部實(shí)例屬性的一個(gè)子集的方法不同，例如決策樹學(xué)習(xí)系統(tǒng)。
比如這樣一個(gè)問題：每個(gè)實(shí)例由20個(gè)屬性描述，但在這些屬性中僅有2個(gè)與它的分類是有關(guān)。在這種情況下，這兩個(gè)相關(guān)屬性的值一致的實(shí)例可能在這個(gè)20維的實(shí)例空間中相距很遠(yuǎn)。結(jié)果，依賴這20個(gè)屬性的相似性度量會(huì)誤導(dǎo)k-近鄰算法的分類。近鄰間的距離會(huì)被大量的不相關(guān)屬性所支配。這種由于存在很多不相關(guān)屬性所導(dǎo)致的難題，有時(shí)被稱為維度災(zāi)難（curse of dimensionality）。最近鄰方法對(duì)這個(gè)問題特別敏感。
解決方法： 當(dāng)計(jì)算兩個(gè)實(shí)例間的距離時(shí)對(duì)每個(gè)屬性加權(quán)。
這相當(dāng)于按比例縮放歐氏空間中的坐標(biāo)軸，縮短對(duì)應(yīng)于不太相關(guān)屬性的坐標(biāo)軸，拉長(zhǎng)對(duì)應(yīng)于更相關(guān)的屬性的坐標(biāo)軸。每個(gè)坐標(biāo)軸應(yīng)伸展的數(shù)量可以通過(guò)交叉驗(yàn)證的方法自動(dòng)決定。
2. 問題二： 應(yīng)用k-近鄰算法的另外一個(gè)實(shí)踐問題是如何建立高效的索引。因?yàn)檫@個(gè)算法推遲所有的處理，直到接收到一個(gè)新的查詢，所以處理每個(gè)新查詢可能需要大量的計(jì)算。
解決方法： 目前已經(jīng)開發(fā)了很多方法用來(lái)對(duì)存儲(chǔ)的訓(xùn)練樣例進(jìn)行索引，以便在增加一定存儲(chǔ)開銷情況下更高效地確定最近鄰。一種索引方法是kd-tree（Bentley 1975；Friedman et al. 1977），它把實(shí)例存儲(chǔ)在樹的葉結(jié)點(diǎn)內(nèi)，鄰近的實(shí)例存儲(chǔ)在同一個(gè)或附近的結(jié)點(diǎn)內(nèi)。通過(guò)測(cè)試新查詢xq的選定屬性，樹的內(nèi)部結(jié)點(diǎn)把查詢xq排列到相關(guān)的葉結(jié)點(diǎn)。
1. 關(guān)于k的取值
K：臨近數(shù)，即在預(yù)測(cè)目標(biāo)點(diǎn)時(shí)取幾個(gè)臨近的點(diǎn)來(lái)預(yù)測(cè)。
K值得選取非常重要，因?yàn)椋?/span>
如果當(dāng)K的取值過(guò)小時(shí)，一旦有噪聲得成分存在們將會(huì)對(duì)預(yù)測(cè)產(chǎn)生比較大影響，例如取K值為1時(shí)，一旦最近的一個(gè)點(diǎn)是噪聲，那么就會(huì)出現(xiàn)偏差，K值的減小就意味著整體模型變得復(fù)雜，容易發(fā)生過(guò)擬合；
如果K的值取的過(guò)大時(shí)，就相當(dāng)于用較大鄰域中的訓(xùn)練實(shí)例進(jìn)行預(yù)測(cè)，學(xué)習(xí)的近似誤差會(huì)增大。這時(shí)與輸入目標(biāo)點(diǎn)較遠(yuǎn)實(shí)例也會(huì)對(duì)預(yù)測(cè)起作用，使預(yù)測(cè)發(fā)生錯(cuò)誤。K值的增大就意味著整體的模型變得簡(jiǎn)單；
如果K==N的時(shí)候，那么就是取全部的實(shí)例，即為取實(shí)例中某分類下最多的點(diǎn)，就對(duì)預(yù)測(cè)沒有什么實(shí)際的意義了；
K的取值盡量要取奇數(shù)，以保證在計(jì)算結(jié)果最后會(huì)產(chǎn)生一個(gè)較多的類別，如果取偶數(shù)可能會(huì)產(chǎn)生相等的情況，不利于預(yù)測(cè)。
K的取法：
常用的方法是從k=1開始，使用檢驗(yàn)集估計(jì)分類器的誤差率。重復(fù)該過(guò)程，每次K增值1，允許增加一個(gè)近鄰。選取產(chǎn)生最小誤差率的K。
一般k的取值不超過(guò)20，上限是n的開方，隨著數(shù)據(jù)集的增大，K的值也要增大。
2.關(guān)于距離的選取
距離就是平面上兩個(gè)點(diǎn)的直線距離
關(guān)于距離的度量方法，常用的有：歐幾里得距離、余弦值（cos）, 相關(guān)度 （correlation）, 曼哈頓距離 （Manhattan distance）或其他。
Euclidean Distance 定義：
兩個(gè)點(diǎn)或元組P1=（x1，y1）和P2=（x2，y2）的歐幾里得距離是
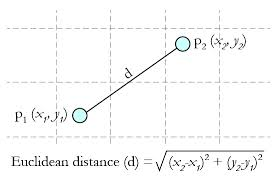
距離公式為：（多個(gè)維度的時(shí)候是多個(gè)維度各自求差）
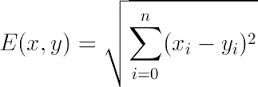
3.相似性度量
相似性一般用空間內(nèi)兩個(gè)點(diǎn)的距離來(lái)度量。距離越大，表示兩個(gè)越不相似。
作為相似性度量的距離函數(shù)一般滿足下列性質(zhì):
d(X,Y)=d(Y,X);
d(X,Y)≦d(X,Z)+d(Z,Y);
d(X,Y)≧0;
d(X,Y)=0,當(dāng)且僅當(dāng)X=Y;
這里，X,Y和Z是對(duì)應(yīng)特征空間中的三個(gè)點(diǎn)。
假設(shè)X,Y分別是N維特征空間中的一個(gè)點(diǎn)，其中X=(x1,x2,…,xn)T,Y=(y1,y2,…,yn)T,d(X,Y)表示相應(yīng)的距離函數(shù)，它給出了X和Y之間的距離測(cè)度。
距離的選擇有很多種，常用的距離函數(shù)如下：
明考斯基(Minkowsky)距離?
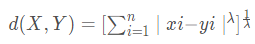, λ一般取整數(shù)值，不同的λ取值對(duì)應(yīng)于不同的
距離
曼哈頓(Manhattan)距離
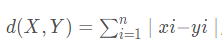，該距離是Minkowsky距離在λ=1時(shí)的一個(gè)特例
Cityblock距離?
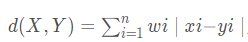，該距離是Manhattan距離的加權(quán)修正，其中wi,i=1,2,…,n是權(quán)重因子。
歐幾里德(Euclidean)距離（歐氏距離）
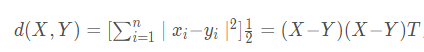，是Minkowsky距離在λ=2時(shí)的特例
Canberra距離
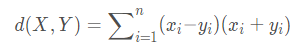
6. Mahalanobis距離(馬式距離)
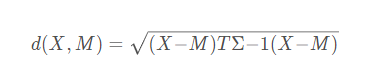
??d(X,M)給出了特征空間中的點(diǎn)X和M之間的一種距離測(cè)度，其中M為某一個(gè)模式類別的均值向量，∑為相應(yīng)模式類別的協(xié)方差矩陣。
??該距離測(cè)度考慮了以M為代表的模式類別在特征空間中的總體分布,能夠緩解由于屬性的線性組合帶來(lái)的距離失真。易見，到M的馬式距離為常數(shù)的點(diǎn)組成特征空間中的一個(gè)超橢球面。
切比雪夫(Chebyshev)距離
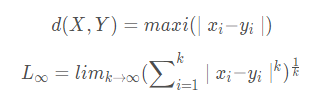
??切比雪夫距離或是L∞度量是向量空間中的一種度量，二個(gè)點(diǎn)之間的距離定義為其各坐標(biāo)數(shù)值差的最大值。在二維空間中。以(x1,y1)和(x2,y2)二點(diǎn)為例，其切比雪夫距離為
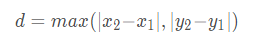
平均距離
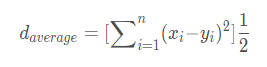
4. 消極學(xué)習(xí)與積極學(xué)習(xí)
(1) 積極學(xué)習(xí)(Eager Learning)
這種學(xué)習(xí)方式是指在進(jìn)行某種判斷（例如，確定一個(gè)點(diǎn)的分類或者回歸中確定某個(gè)點(diǎn)對(duì)應(yīng)的函數(shù)值）之前，先利用訓(xùn)練數(shù)據(jù)進(jìn)行訓(xùn)練得到一個(gè)目標(biāo)函數(shù)，待需要時(shí)就只利用訓(xùn)練好的函數(shù)進(jìn)行決策，顯然這是一種一勞永逸的方法，SVM就屬于這種學(xué)習(xí)方式。
(2) 消極學(xué)習(xí)(Lazy Learning)
這種學(xué)習(xí)方式指不是根據(jù)樣本建立一般化的目標(biāo)函數(shù)并確定其參數(shù)，而是簡(jiǎn)單地把訓(xùn)練樣本存儲(chǔ)起來(lái)，直到需要分類新的實(shí)例時(shí)才分析其與所存儲(chǔ)樣例的關(guān)系，據(jù)此確定新實(shí)例的目標(biāo)函數(shù)值。也就是說(shuō)這種學(xué)習(xí)方式只有到了需要決策時(shí)才會(huì)利用已有數(shù)據(jù)進(jìn)行決策，而在這之前不會(huì)經(jīng)歷 Eager Learning所擁有的訓(xùn)練過(guò)程。KNN就屬于這種學(xué)習(xí)方式。
比較
(3) 比較
Eager Learning考慮到了所有訓(xùn)練樣本，說(shuō)明它是一個(gè)全局的近似，雖然它需要耗費(fèi)訓(xùn)練時(shí)間，但它的決策時(shí)間基本為0.
Lazy Learning在決策時(shí)雖然需要計(jì)算所有樣本與查詢點(diǎn)的距離，但是在真正做決策時(shí)卻只用了局部的幾個(gè)訓(xùn)練數(shù)據(jù)，所以它是一個(gè)局部的近似，然而雖然不需要訓(xùn)練，它的復(fù)雜度還是需要 O(n),n 是訓(xùn)練樣本的個(gè)數(shù)。由于每次決策都需要與每一個(gè)訓(xùn)練樣本求距離，這引出了Lazy Learning的缺點(diǎn)：(1)需要的存儲(chǔ)空間比較大 (2)決策過(guò)程比較慢。
(4) 典型算法
積極學(xué)習(xí)方法:SVM;Find-S算法;候選消除算法;決策樹;人工神經(jīng)網(wǎng)絡(luò);貝葉斯方法;
消極學(xué)習(xí)方法:KNN;局部加權(quán)回歸;基于案例的推理;
05
sklearn庫(kù)的應(yīng)用
我利用了sklearn庫(kù)來(lái)進(jìn)行了KNN的應(yīng)用（這個(gè)庫(kù)是真的很方便了，可以借助這個(gè)庫(kù)好好學(xué)習(xí)一下，我是用KNN算法進(jìn)行了根據(jù)成績(jī)來(lái)預(yù)測(cè)，這里用一個(gè)花瓣萼片的實(shí)例，因?yàn)檫@篇主要是關(guān)于KNN的知識(shí)，所以不對(duì)sklearn的過(guò)多的分析，而且我用的還不深入??）
sklearn庫(kù)內(nèi)的算法與自己手搓的相比功能更強(qiáng)大、拓展性更優(yōu)異、易用性也更強(qiáng)。還是很受歡迎的。（確實(shí)好用，簡(jiǎn)單）
from sklearn import neighbors //包含有kNN算法的模塊
from sklearn import datasets //一些數(shù)據(jù)集的模塊
調(diào)用KNN的分類器
knn = neighbors.KNeighborsClassifier()
預(yù)測(cè)花瓣代碼
from sklearn import neighbors
from sklearn import datasets
knn = neighbors.KNeighborsClassifier()
iris = datasets.load_iris()
# f = open("iris.data.csv", 'wb') #可以保存數(shù)據(jù)
# f.write(str(iris))
# f.close()
print iris
knn.fit(iris.data, iris.target) #用KNN的分類器進(jìn)行建模，這里利用的默認(rèn)的參數(shù)，大家可以自行查閱文檔
predictedLabel = knn.predict([[0.1, 0.2, 0.3, 0.4]])
print ("predictedLabel is :" + predictedLabel)
上面的例子是只預(yù)測(cè)了一個(gè)，也可以進(jìn)行數(shù)據(jù)集的拆分，將數(shù)據(jù)集劃分為訓(xùn)練集和測(cè)試集
from sklearn.mode_selection import train_test_split #引入數(shù)據(jù)集拆分的模塊
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
關(guān)于 train_test_split 函數(shù)參數(shù)的說(shuō)明：
??train_data：被劃分的樣本特征集
??train_target：被劃分的樣本標(biāo)簽
??test_size：float-獲得多大比重的測(cè)試樣本 （默認(rèn)：0.25）
??int - 獲得多少個(gè)測(cè)試樣本
??random_state：是隨機(jī)數(shù)的種子。
文獻(xiàn)資料
[1] Trevor Hastie & Rolbert Tibshirani. Discriminant Adaptive Nearest Neighbor Classification. IEEE TRANSACTIONS ON PATTERN ANALYSIS AND MACHINE INTELLIGENCE,1996.
[2] R. Short & K. Fukanaga. A New Nearest Neighbor Distance Measure, Pro. Fifth IEEE Int’l Conf.Pattern Recognition,pp.81-86,1980.
[3] T.M Cover. Nearest Neighbor Pattern Classification, Pro. IEEE Trans, Infomation Theory,1967.
[4] C.J.Stone. Consistent Nonparametric Regression, Ann.Stat.,vol.3,No.4,pp.595-645,1977.
[5] W Cleveland. Robust Locally-Weighted Regression and Smoothing Scatterplots, J.Am.Statistical.,vol.74,pp.829-836,1979.
[6] T.A.Brown & J.Koplowitz. The Weighted Nearest Neighbor Rule for Class Dependent Sample Sizes, IEEE Tran. Inform. Theory, vol.IT-25,pp.617-619,Sept.1979.
[7] J.P.Myles & D.J.Hand. The Multi-Class Metric Problem in Nearest Neighbor Discrimination Rules, Pattern Recognition,1990.
[8] N.S.Altman. An Introduction to Kernel and Nearest Neighbor Nonparametric Regression,1992.
[9]Min-Ling Zhang & Zhi-Hua Zhou. M1-KNN: A Lazy Learning Approach to Multi-Label Learning,2007.
[10]Peter Hall, Byeong U.Park & Richard J. Samworth. Choice of Neighbor Order In Nearest Neighbor Classification,2008.
[11] Jia Pan & Dinesh Manocha. Bi-Level Locality Sensitive Hashing for K-Nearest Neighbor Computation,2012.
往期精彩回顧 本站qq群851320808，加入微信群請(qǐng)掃碼：