數(shù)學推導+純Python實現(xiàn)機器學習算法22:EM算法

Python機器學習算法實現(xiàn)

Author：louwill

Machine Learning Lab

? ? ?

? ? 從本篇開始，整個機器學習系列還剩下最后三篇涉及導概率模型的文章，分別是EM算法、CRF條件隨機場和HMM隱馬爾科夫模型。本文主要講解一下EM（Expection maximization），即期望最大化算法。EM算法是一種用于包含隱變量概率模型參數(shù)的極大似然估計方法，所以本文從極大似然方法說起，然后推廣到EM算法。

極大似然估計

? ? 統(tǒng)計學專業(yè)的朋友對于極大似然估計一定是很熟悉了。極大似然是一種統(tǒng)計參數(shù)估計方法，對于某個隨機樣本滿足某種概率分布，但其中的統(tǒng)計參數(shù)未知，我們通過若干次試驗結果來估計參數(shù)的值的方法。

? ? 舉個例子來說。比如說我們想了解一下某校學生的身高分布。我們先假設該校學生身高服從一個正態(tài)分布，其中的分布參數(shù)和未知。全校大幾萬的學生，我們要一個個去實測肯定不現(xiàn)實。所以我們決定用統(tǒng)計抽樣的方法，隨機選取100名學生來看一下身高。

? ? 要通過這100人的身高來估算全校學生的身高，我們需要明確下面幾個問題。第一個就是抽到這100人的概率是多少，因為每個人的選取都是獨立的，所以選到這100人的概率可以表示為單個概率的乘積：

? ? 上式即為似然函數(shù)。通常為了計算方便，我們會對似然函數(shù)取對數(shù)：

? ? 第二個問題在于我們要解釋一下為什么能夠剛好抽到這100人。所以按照極大似然估計的理論，在學校這么多人中，我們恰好抽到這100人而不是另外的100人，正是因為這100人出現(xiàn)的概率極大，即其對應的似然函數(shù)極大：

? ? 第三個問題在于如何求解。這個好辦，直接對求其參數(shù)的偏導數(shù)并令為0即可。

? ? 所以極大似然估計法可以看作由抽樣結果對條件的反推，即已知某個參數(shù)能使這些樣本出現(xiàn)的概率極大，我們就直接把該參數(shù)作為參數(shù)估計的真實值。

EM算法引入

? ? 上述基于全校學生身高服從一個分布的假設過于籠統(tǒng)，實際上該校男女生的身高分布是不一樣的。其中男生的身高分布為，女生的身高分布為。現(xiàn)在我們估計該校學生的分布，就不能簡單的一刀切了。

? ? 你可以說我們分別抽選50個男生和50個女生，對其分開進行估計。但大多數(shù)情況下，我們并不知道抽樣得到的這個樣本是來自于男生還是女生。如果說學生的身高的觀測變量（Observable Variable），那么樣本性別就是一種隱變量（Hidden Variable）。

? ? 在這種情況下，我們需要估計的問題包括兩個：一個是這個樣本是男的還是女的，二是男生和女生對應身高的正態(tài)分布參數(shù)分別是多少。這種情況下常規(guī)的極大似然估計就不太好使了，要估計男女身高分布，那必須先估計該學生是男還是女，反過來要估計該學生是男還是女，又得從身高來判斷（男生身高相對較高，女生身高相對較矮）。但二者相互依賴，直接用極大似然估計沒法算。

? ? 針對這種包含隱變量的參數(shù)估計問題，一般使用EM算法來進行求解。針對上述身高估計問題，EM算法的求解思想認為：既然兩個問題相互依賴，肯定是一個動態(tài)求解過程。不如我們直接給定男生女生身高的分布初始值，根據初始值估計每個樣本是男還是女的概率（E步），然后據此使用極大似然估計男女生的身高分布參數(shù)（M步），之后動態(tài)迭代調整直到滿足終止條件為止。

EM算法

? ? 所以EM算法的應用場景就是要解決包含隱變量的概率模型參數(shù)估計問題。給定觀測變量數(shù)據，隱變量數(shù)據，聯(lián)合概率分布以及關于隱變量的條件分布，使用EM算法對模型參數(shù)進行估計流程如下：

• 初始化模型參數(shù)，進行迭代：
• E步：記為第次迭代參數(shù)的估計值，在第次迭代的E步，計算函數(shù)：
  其中為給定觀測數(shù)據和當前參數(shù)估計下隱變量數(shù)據的條件概率分布；
• M步：求使函數(shù)最大化的參數(shù)，確定第次迭代的參數(shù)估計值：
• 重復迭代E步和M步直至收斂。

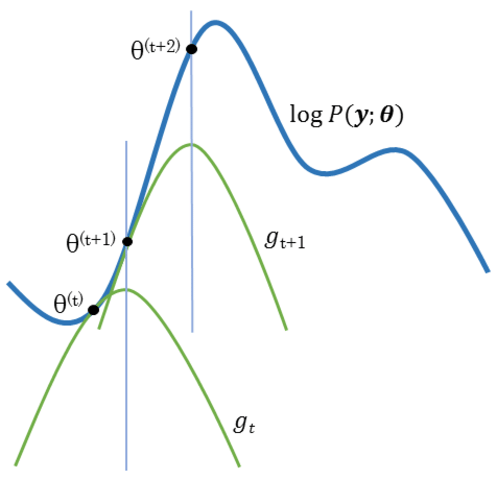
? ? 由EM算法過程我們可以看到，其關鍵在于E步要確定函數(shù)，E步在固定模型參數(shù)的情況下來估計隱變量分布，而M步則是固定隱變量來估計模型參數(shù)。二者交互進行，直至滿足算法收斂條件。

三硬幣模型

? ? EM算法的一個經典例子是三硬幣模型。假設有A，B，C三枚硬幣，其出現(xiàn)正面的概率分別為，和。使用三枚硬幣進行如下試驗：先拋擲硬幣A，根據其結果來選擇硬幣B或者C，假設正面選B，反面選C，然后記錄硬幣結果，正面記為1，反面記為0，獨立重復5次試驗，每次試驗重復拋擲B或者C10次。問如何估計三枚硬幣分別出現(xiàn)正面的概率。

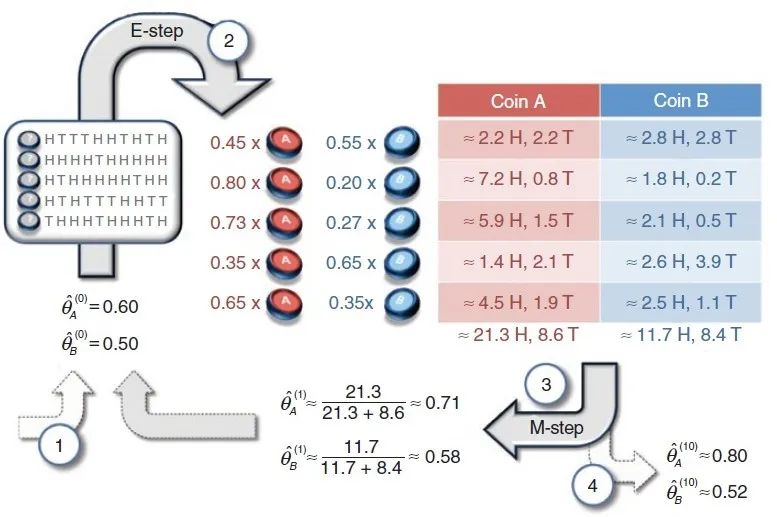
三硬幣模型

? ? 由于我們只能觀察到最后的拋擲結果，至于這個結果是由硬幣A拋出來的還是由硬幣B拋出來的，我們無從知曉。所以這個過程中依概率選擇哪一個硬幣拋擲就是一個隱變量。因此我們需要使用EM算法來進行求解。

? ? E步：初始化B和C出現(xiàn)正面的概率為和，估計每次試驗中選擇B還是C的概率（即硬幣A是正面還是反面的概率），例如選擇B的概率為：

? ? 相應的選擇C的概率為。計算出每次試驗選擇B和C的概率，然后根據試驗數(shù)據進行加權求和。

? ? M步：更新模型參數(shù)的新估計值。根據函數(shù)求導來確定參數(shù)值：

? ? 對上式求導并令為0可得第一次迭代后的參數(shù)值：，然后重復進行第二輪、第三輪...直至模型收斂。

EM算法簡易實現(xiàn)

? ? 下面我們用numpy來實現(xiàn)一個簡單的EM算法過程來求解三硬幣問題。完整代碼如下：

import numpy as np
def em(data, thetas, max_iter=50, eps=1e-3):    '''    data：觀測數(shù)據    thetas：估計參數(shù)    max_iter：最大迭代次數(shù)    eps：收斂閾值    '''    # 初始化似然函數(shù)值    ll_old = -np.infty    for i in range(max_iter):        ### E步：求隱變量分布        # 對數(shù)似然        log_like = np.array([np.sum(data * np.log(theta), axis=1) for theta in thetas])        # 似然        like = np.exp(log_like)        # 求隱變量分布        ws = like/like.sum(0)        # 概率加權        vs = np.array([w[:, None] * data for w in ws])        ### M步：更新參數(shù)值        thetas = np.array([v.sum(0)/v.sum() for v in vs])        # 更新似然函數(shù)        ll_new = np.sum([w*l for w, l in zip(ws, log_like)])        print("Iteration: %d" % (i+1))        print("theta_B = %.2f, theta_C = %.2f, ll = %.2f"               % (thetas[0,0], thetas[1,0], ll_new))        # 滿足迭代條件即退出迭代        if np.abs(ll_new - ll_old) < eps:            break        ll_old = ll_new    return thetas

基于我們編寫的EM算法函數(shù)來對三硬幣問題進行求解：

# 觀測數(shù)據，5次獨立試驗，每次試驗10次拋擲的正反次數(shù)# 比如第一次試驗為5次正面5次反面observed_data = np.array([(5,5), (9,1), (8,2), (4,6), (7,3)])# 初始化參數(shù)值，即硬幣B的正面概率為0.6，硬幣C的正面概率為0.5thetas = np.array([[0.6, 0.4], [0.5, 0.5]])eps = 0.01max_iter = 50thetas = em(observed_data, thetas, max_iter=50, eps=1e-3)

迭代過程如下：

Iteration: 1theta_B = 0.71, theta_C = 0.58, ll = -32.69Iteration: 2theta_B = 0.75, theta_C = 0.57, ll = -31.26Iteration: 3theta_B = 0.77, theta_C = 0.55, ll = -30.76Iteration: 4theta_B = 0.78, theta_C = 0.53, ll = -30.33Iteration: 5theta_B = 0.79, theta_C = 0.53, ll = -30.07Iteration: 6theta_B = 0.79, theta_C = 0.52, ll = -29.95Iteration: 7theta_B = 0.80, theta_C = 0.52, ll = -29.90Iteration: 8theta_B = 0.80, theta_C = 0.52, ll = -29.88Iteration: 9theta_B = 0.80, theta_C = 0.52, ll = -29.87Iteration: 10theta_B = 0.80, theta_C = 0.52, ll = -29.87Iteration: 11theta_B = 0.80, theta_C = 0.52, ll = -29.87Iteration: 12theta_B = 0.80, theta_C = 0.52, ll = -29.87

? ? 可以看到，算法在第七次時達到收斂，最后硬幣B和C的正面概率分別為0.8和0.52。

? ? 關于EM算法，本文沒有太多深入的解釋，關于似然函數(shù)下界的推導，EM算法的多種解釋等，感興趣的朋友可以自行查找資料學習。

參考資料：

李航 統(tǒng)計學習方法 第二版

https://zhuanlan.zhihu.com/p/36331115

往期精彩：

數(shù)學推導+純Python實現(xiàn)機器學習算法20：隨機森林

一個算法工程師的成長之路

長按二維碼.關注機器學習實驗室

喜歡您就點個在看！