【機(jī)器學(xué)習(xí)】主成分分析（PCA）：通過(guò)圖像可視化深入理解
主成分分析（PCA）是一種廣泛應(yīng)用于機(jī)器學(xué)習(xí)的降維技術(shù)。PCA 通過(guò)對(duì)大量變量進(jìn)行某種變換，將這些變量中的信息壓縮為較少的變量。變換的應(yīng)用方式是將線性相關(guān)變量變換為不相關(guān)變量。相關(guān)性告訴我們存在信息冗余，如果可以減少這種冗余，則可以壓縮信息。例如，如果變量集中有兩個(gè)高度相關(guān)的變量，那么通過(guò)保留這兩個(gè)變量我們不會(huì)獲得任何額外信息，因?yàn)橐粋€(gè)變量幾乎可以表示為另一個(gè)的線性組合。在這種情況下，PCA 通過(guò)平移和旋轉(zhuǎn)原始軸并將數(shù)據(jù)投影到新軸上，將第二個(gè)變量的方差轉(zhuǎn)移到第一個(gè)變量上，使用特征值和特征向量確定投影方向。因此，前幾個(gè)變換后的特征（稱為主成分）信息豐富，而最后一個(gè)特征主要包含噪聲，其中的信息可以忽略不計(jì)。這種可轉(zhuǎn)移性使我們能夠保留前幾個(gè)主成分，從而顯著減少變量數(shù)量，同時(shí)將信息損失降至最低。
本文更多地關(guān)注圖像數(shù)據(jù)上的實(shí)際逐步 PCA 實(shí)現(xiàn)，而不是理論上的解釋，因?yàn)橐呀?jīng)有大量的材料可用于此。選擇了圖像數(shù)據(jù)而不是表格數(shù)據(jù)，以便我們可以通過(guò)圖像可視化更好地理解 PCA 的工作。從技術(shù)上講，圖像是像素矩陣，其亮度表示該像素內(nèi)表面特征的反射率。對(duì)于 8 位整數(shù)圖像，反射率值的范圍為 0 到 255。因此，具有零反射率的像素將顯示為黑色，值為 255 的像素顯示為純白色，值介于兩者之間的像素顯示為灰色調(diào)。文章中使用了在印度沿海地區(qū)拍攝的 Landsat TM 衛(wèi)星圖像。圖像被調(diào)整為較小的比例以減少 CPU 上的計(jì)算負(fù)載。該圖像集由在藍(lán)色、綠色、紅色、近紅外 (NIR) 和中紅外 (MIR) 電磁光譜范圍內(nèi)捕獲的 7 個(gè)波段圖像組成。
第一步是導(dǎo)入所需的庫(kù)并加載數(shù)據(jù)。為了便于使訪問和處理，波段圖像被堆疊在大小為 850 x 1100 x 7（高 x 寬 x 波段數(shù)）的 3d numpy 陣列中。下面顯示的彩色圖像是紅色、綠色和藍(lán)色 (RGB) 波段圖像的合成，再現(xiàn)了與我們所看到的相同的視圖。
from IPython.display import Image, displayimport matplotlib.pyplot as pltimport pandas as pdimport seaborn as snsimport cv2import numpy as np# Read RGB image into an arrayimg = cv2.imread('band321.jpg')img_shape = img.shape[:2]print('image size = ',img_shape)# specify no of bands in the imagen_bands = 7# 3 dimensional dummy array with zerosMB_img = np.zeros((img_shape[0],img_shape[1],n_bands))# stacking up images into the arrayfor i in range(n_bands):MB_img[:,:,i] = cv2.imread('band'+str(i+1)+'.jpg',cv2.IMREAD_GRAYSCALE)# Let's take a look at sceneprint('\n\nDispalying colour image of the scene')plt.figure(figsize=(img_shape[0]/100,img_shape[1]/100))plt.imshow(img, vmin=0, vmax=255)plt.axis('off');
圖像場(chǎng)景包括各種地表特征，例如水、建筑面積、森林和農(nóng)田。
讓我們看一下不同特征的單個(gè)波段圖像的反射率，并嘗試深入了解波段圖像中的特征。
import matplotlib.pyplot as pltimport matplotlib.gridspec as gridfig,axes = plt.subplots(2,4,figsize=(50,23),sharex='all', sharey='all')fig.subplots_adjust(wspace=0.1, hspace=0.15)fig.suptitle('Intensities at Different Bandwidth in the visible and Infra-red spectrum', fontsize=30)axes = axes.ravel()for i in range(n_bands):axes[i].imshow(MB_img[:,:,i],cmap='gray', vmin=0, vmax=255)axes[i].set_title('band '+str(i+1),fontsize=25)axes[i].axis('off')fig.delaxes(axes[-1])
如果我們觀察圖像，所有波段都捕獲了一個(gè)或多個(gè)表面特征，并且每個(gè)特征都在多個(gè)波段中被很好地捕獲。例如，在波段 2（綠色）和波段 4（近紅外）圖像中，農(nóng)田很容易與其他地表特征區(qū)分開來(lái)，但在其他區(qū)域則不易區(qū)分。因此，波段之間存在信息冗余，這意味著各波段之間的反射率有一定的相關(guān)性，這為我們提供了一個(gè)在它們上測(cè)試 PCA 的機(jī)會(huì)。
在應(yīng)用 PCA 之前，我們必須通過(guò)標(biāo)準(zhǔn)化將我們的數(shù)據(jù)轉(zhuǎn)化為通用格式。這樣做的目的是確保變量在內(nèi)部保持一致，而不管它們的類型如何。例如，如果數(shù)據(jù)集有兩個(gè)變量，溫度以攝氏度為單位，降雨量以厘米為單位。由于變量范圍和單位不同，不建議按原樣使用不同的變量，否則數(shù)量級(jí)不同的變量可能會(huì)導(dǎo)致模型對(duì)某些變量的偏差。標(biāo)準(zhǔn)化是通過(guò)減去均值來(lái)使變量居中，然后通過(guò)除以標(biāo)準(zhǔn)差使它們達(dá)到一個(gè)共同的尺度來(lái)完成的。由于我們處理的變量（波段圖像）相似且具有相同的范圍，因此不需要標(biāo)準(zhǔn)化，但仍然可以應(yīng)用。
我們的變量是圖像二維數(shù)組，需要轉(zhuǎn)換為一維向量以便于矩陣計(jì)算。讓我們創(chuàng)建一個(gè)大小為 935000 X 7（圖像中的像素?cái)?shù) X 波段數(shù)）的變量矩陣，并將這些一維向量存儲(chǔ)在其中。
# Convert 2d band array in 1-d to make them as feature vectors and StandardizationMB_matrix = np.zeros((MB_img[:,:,0].size,n_bands))for i in range(n_bands):MB_array = MB_img[:,:,i].flatten() # covert 2d to 1d arrayMB_arrayStd = (MB_array - MB_array.mean())/MB_array.std()MB_matrix[:,i] = MB_arrayStdMB_matrix.shape;
讓我們進(jìn)一步了解 PCA 中發(fā)生的軸變換。下面的散點(diǎn)圖顯示了綠色和紅色波段數(shù)據(jù)之間的相關(guān)性。然后使用特征向量確定主分量軸 (X2, Y2)，使得沿 X2 方向的方差最大，而與其正交的方向使 Y2 的方差最小。原始軸 (X1, Y1) 現(xiàn)在沿主分量軸 (X2, Y2) 旋轉(zhuǎn)，投影到這些新軸上的數(shù)據(jù)是主分量。需要注意的是，原始數(shù)據(jù)中存在的相關(guān)性在轉(zhuǎn)換到 (X2, Y2) 空間后被消除，而方差部分從一個(gè)變量轉(zhuǎn)移到另一個(gè)變量。
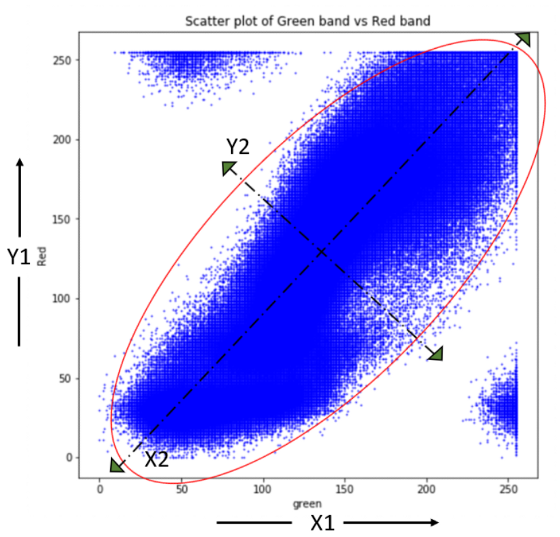
下一步是計(jì)算協(xié)方差矩陣的特征向量和對(duì)應(yīng)的特征值
# Covariancenp.set_printoptions(precision=3)cov = np.cov(MB_matrix.transpose())# Eigen ValuesEigVal,EigVec = np.linalg.eig(cov)print("Eigenvalues:\n\n", EigVal,"\n")
特征值：
[5.508 0.796 0.249 0.167 0.088 0.064 0.128]
在這一步中，實(shí)現(xiàn)數(shù)據(jù)壓縮和降維。如果我們觀察特征值，我們會(huì)發(fā)現(xiàn)這些值完全不同。這些值為我們提供了特征向量或方向的重要性順序，即沿著特征向量的軸具有最大的特征值，是最重要的 PC 軸，依此類推。下一步是根據(jù)特征值從高到低對(duì)特征向量進(jìn)行排序，按重要性順序重新排列主成分。我們需要在有序特征向量的方向上轉(zhuǎn)換數(shù)據(jù)，而有序特征向量又會(huì)產(chǎn)生主成分。
# Ordering Eigen values and vectorsorder = EigVal.argsort()[::-1]EigVal = EigVal[order]EigVec = EigVec[:,order]#Projecting data on Eigen vector directions resulting to Principal ComponentsPC = np.matmul(MB_matrix,EigVec) #cross product
依賴性檢查
我們能夠成功地生產(chǎn)主要成分。現(xiàn)在，讓我們驗(yàn)證 PC 以檢查它們是否能夠減少冗余，并檢查實(shí)現(xiàn)數(shù)據(jù)壓縮的程度。我們將創(chuàng)建散點(diǎn)圖來(lái)可視化原始波段中的成對(duì)關(guān)系，并將其與 PC 的成對(duì)關(guān)系進(jìn)行比較以測(cè)試是否存在依賴性。
# Generate Paiplot for original data and transformed PCsBandnames = ['Band 1','Band 2','Band 3','Band 4','Band 5','Band 6','Band 7']a = sns.pairplot(pd.DataFrame(MB_matrix,columns = Bandnames),diag_kind='kde',plot_kws={"s": 3})a.fig.suptitle("Pair plot of Band images")PCnames = ['PC 1','PC 2','PC 3','PC 4','PC 5','PC 6','PC 7']b = sns.pairplot(pd.DataFrame(PC,columns = PCnames),diag_kind='kde',plot_kws={"s": 3})b.fig.suptitle("Pair plot of PCs")
波段（左）和 PCs（右）的配對(duì)圖
讓我們看一下配對(duì)圖，并注意到原始數(shù)據(jù)中存在的變量之間的相關(guān)性在主成分中消失了。因此，PCA 能夠顯著降低相關(guān)性。沿對(duì)角線的分布圖告訴我們，PCA 也成功地轉(zhuǎn)移了與可壓縮性相關(guān)的方差。
壓縮性檢查
#Information Retained by Principal Componentsplt.figure(figsize=(8,6))plt.bar([1,2,3,4,5,6,7],EigVal/sum(EigVal)*100,align='center',width=0.4,tick_label = ['PC1','PC2','PC3','PC4','PC5','PC6','PC7'])plt.ylabel('Variance (%)')plt.title('Information retention');
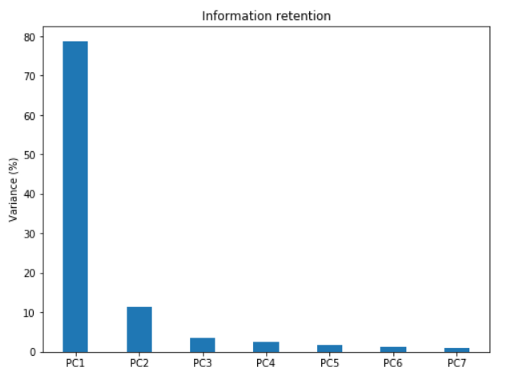
上面繪制的以百分比表示的特征值條形圖為我們提供了每個(gè) PC 中保留的信息。請(qǐng)注意，最后一個(gè) PC 的特征值很小且不那么重要，這就是降維的作用所在。如果我們選擇保留 93% 信息的前三個(gè)相關(guān)組件，那么最終數(shù)據(jù)可以從 7 維減少到 3 維，而不會(huì)丟失太多信息。
是時(shí)候?qū)⒁痪S PC 重塑回原始圖像形狀并將PCs在 0 到 255 之間進(jìn)行歸一化，這與原始圖像范圍相同，以使圖像可視化成為可能。
# Rearranging 1-d arrays to 2-d arrays of image sizePC_2d = np.zeros((img_shape[0],img_shape[1],n_bands))for i in range(n_bands):PC_2d[:,:,i] = PC[:,i].reshape(-1,img_shape[1])# normalizing between 0 to 255PC_2d_Norm = np.zeros((img_shape[0],img_shape[1],n_bands))for i in range(n_bands):PC_2d_Norm[:,:,i] = cv2.normalize(PC_2d[:,:,i],np.zeros(img_shape),0,255 ,cv2.NORM_MINMAX)
讓我們直觀地確定壓縮量。
fig,axes = plt.subplots(2,4,figsize=(50,23),sharex='all',sharey='all')fig.subplots_adjust(wspace=0.1, hspace=0.15)fig.suptitle('Intensities of Principal Components ', fontsize=30)axes = axes.ravel()for i in range(n_bands):axes[i].imshow(PC_2d_Norm[:,:,i],cmap='gray', vmin=0, vmax=255)axes[i].set_title('PC '+str(i+1),fontsize=25)axes[i].axis('off')fig.delaxes(axes[-1])
主成分圖像的強(qiáng)度
請(qǐng)注意，前幾個(gè) PCs 具有豐富的信息并且很清晰，隨著我們接近尾聲，PCs 開始丟失信息，而最后幾個(gè) PCs 大多包含噪聲。我們將保留前三個(gè) PCs 并丟棄其余的。這將有助于通過(guò)去除噪聲改善數(shù)據(jù)質(zhì)量，并通過(guò)機(jī)器學(xué)習(xí)算法進(jìn)行處理，在時(shí)間和內(nèi)存使用方面效率更高。
# Comparsion of RGB and Image produced using first three bandsfig,axes = plt.subplots(1,2,figsize=(50,23),sharex='all', sharey='all')fig.subplots_adjust(wspace=0.1, hspace=0.15)axes[0].imshow(MB_img[:,:,0:3].astype(int))axes[0].axis('off');axes[1].imshow(PC_2d_Norm[:,:,:3][:,:,[0,2,1]].astype(int))axes[1].axis('off');
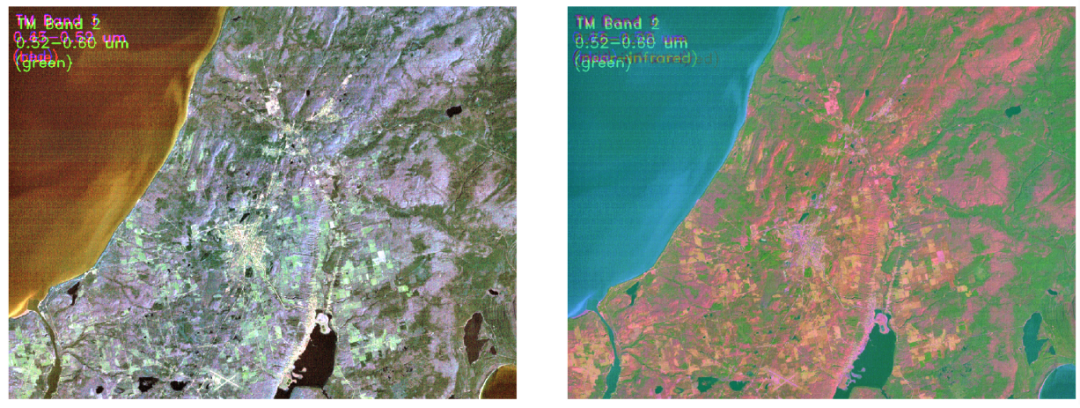RGB 圖像（左）與主成分合成圖像（右）對(duì)比
最后，我們使用前三個(gè)主成分再現(xiàn)了相同的場(chǎng)景。右邊的圖像看起來(lái)比原始圖像 RGB 更豐富多彩，這使得場(chǎng)景中的特征看起來(lái)更清晰，更容易區(qū)分。例如，由于顏色不同，農(nóng)田可以更容易地與城市地區(qū)區(qū)分開來(lái)。一些特征在PC圖中顯得更加圖層，而在左側(cè)圖像中則難以識(shí)別。因此，可以得出結(jié)論，PCA 在可壓縮性和信息保留方面對(duì)我們的圖像數(shù)據(jù)做得很好。
Github代碼連接：
https://github.com/Skumarr53/Principal-Component-Analysis-testing-on-Image-data
往期精彩回顧 本站qq群955171419，加入微信群請(qǐng)掃碼：