主成分分析（PCA）原理總結(jié)
點(diǎn)擊上方“小白學(xué)視覺”，選擇加"星標(biāo)"或“置頂”
重磅干貨，第一時(shí)間送達(dá)
主成分分析（Principal components analysis，以下簡(jiǎn)稱PCA）是最常用的降維方法之一，在數(shù)據(jù)壓縮和消除冗余方面具有廣泛的應(yīng)用，本文由淺入深的對(duì)其降維原理進(jìn)行了詳細(xì)總結(jié)。
1.向量投影和矩陣投影的含義
2. 向量降維和矩陣降維的含義
3. 基向量選擇算法
4. 基向量個(gè)數(shù)的確定
5. 中心化的作用
6. PCA算法流程
7. PCA算法總結(jié)
如下圖：
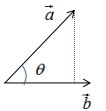
向量a在向量b的投影為：
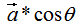
其中，θ是向量間的夾角 。
向量a在向量b的投影表示向量a在向量b方向的信息，若θ=90°時(shí)，向量a與向量b正交，向量a無向量b信息，即向量間無冗余信息 。因此，向量最簡(jiǎn)單的表示方法是用基向量表示，如下圖：
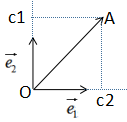
向量表示方法：
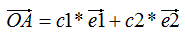
其中，c1是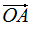
在e1方向的投影，c2是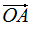在e2方向的投影，e1和e2是基向量
我們用向量的表示方法擴(kuò)展到矩陣，若矩陣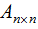
的秩r(A)=n，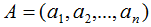
，其中ai（i=1,2,...,n）為n個(gè)維度的列向量，那么矩陣A的列向量表示為：
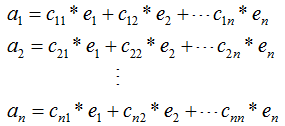
其中，e1，e2，...，en為矩陣A的特征向量 。
若矩陣A是對(duì)稱矩陣，那么特征向量為正交向量，我們對(duì)上式結(jié)合成矩陣的形式：
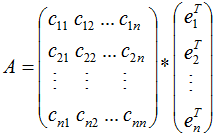
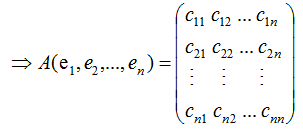
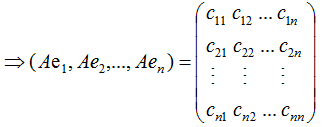
由上式可知，對(duì)稱矩陣A在各特征向量的投影等于矩陣列向量展開后的系數(shù)，特征向量可理解為基向量。
向量降維可以通過投影的方式實(shí)現(xiàn)，N維向量映射為M維向量轉(zhuǎn)換為N維向量在M個(gè)基向量的投影，如N維向量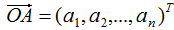
，M個(gè)基向量分別為
，
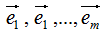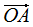在基向量的投影：
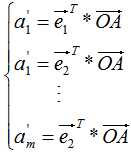
通過上式完成了降維，降維后的坐標(biāo)為：
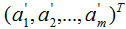
矩陣是由多個(gè)列向量組成的，因此矩陣降維思想與向量降維思想一樣，只要求得矩陣在各基向量的投影即可，基向量可以理解為新的坐標(biāo)系，投影就是降維后的坐標(biāo)，那么問題來了，如何選擇基向量？
已知樣本集的分布，如下圖：
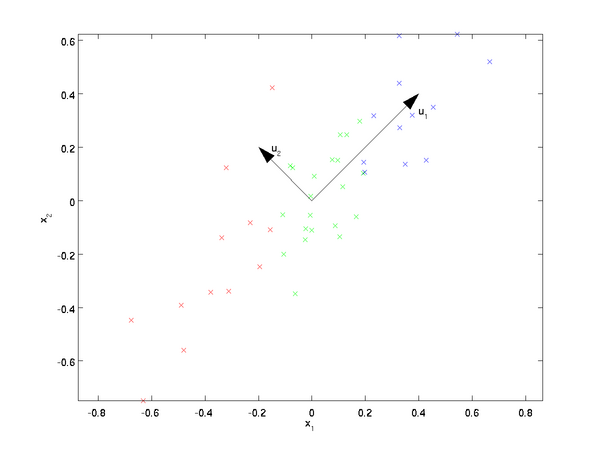
樣本集共有兩個(gè)特征x1和x2，現(xiàn)在對(duì)該樣本數(shù)據(jù)從二維降到一維，圖中列了兩個(gè)基向量u1和u2，樣本集在兩個(gè)向量的投影表示了不同的降維方法，哪種方法好，需要有評(píng)判標(biāo)準(zhǔn)：（1）降維前后樣本點(diǎn)的總距離足夠近，即最小投影距離；（2）降維后的樣本點(diǎn)（投影）盡可能的散開，即最大投影方差 。因此，根據(jù)上面兩個(gè)評(píng)判標(biāo)準(zhǔn)可知選擇基向量u1較好。
我們知道了基向量的選擇標(biāo)準(zhǔn)，下面介紹基于這兩個(gè)評(píng)判標(biāo)準(zhǔn)來推導(dǎo)基向量：
（1）基于最小投影距離
假設(shè)有n個(gè)n維數(shù)據(jù)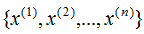
，記為X。現(xiàn)在對(duì)該數(shù)據(jù)從n維降到m維，關(guān)鍵是找到m個(gè)基向量，假設(shè)基向量為{w1,w2,...,wm}，記為矩陣W，矩陣W的大小是n×m。
原始數(shù)據(jù)在基向量的投影：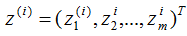
投影坐標(biāo)計(jì)算公式：
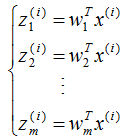
根據(jù)投影坐標(biāo)和基向量，得到該樣本的映射點(diǎn)：
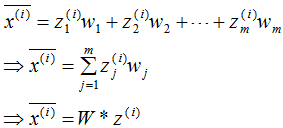
最小化樣本和映射點(diǎn)的總距離：
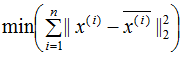
推導(dǎo)上式，得到最小值對(duì)應(yīng)的基向量矩陣W，推導(dǎo)過程如下：
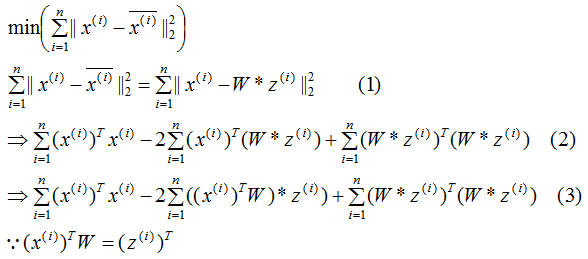
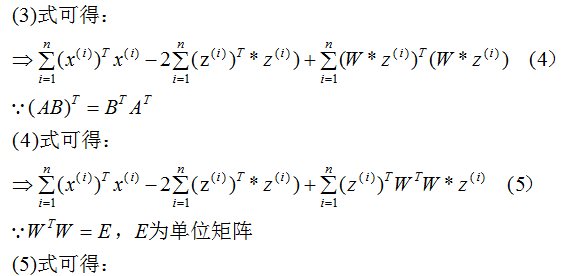
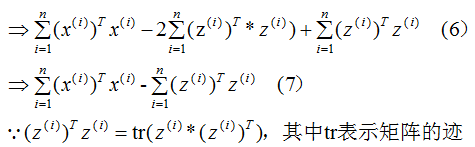
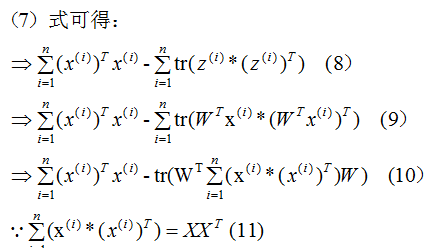
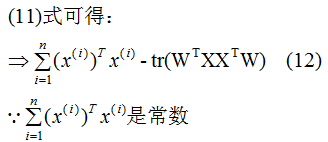
所以我們選擇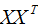
的特征向量作為投影的基向量?。
(2) 基于最大投影方差
我們希望降維后的樣本點(diǎn)盡可能分散，方差可以表示這種分散程度。
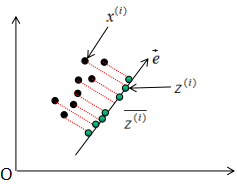
如上圖所示，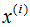
表示原始數(shù)據(jù)，
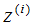表示投影數(shù)據(jù)，
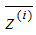表示投影數(shù)據(jù)的平均值。所以最大化投影方差表示為：
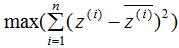
下面推導(dǎo)上式，得到相應(yīng)的基向量矩陣W，推導(dǎo)過程如下：
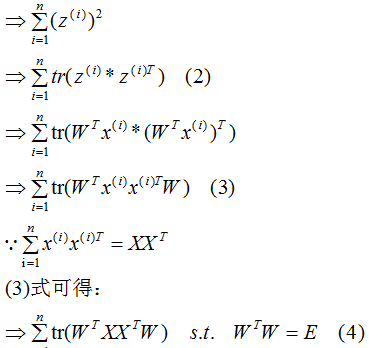
我們發(fā)現(xiàn)(4)式與上一節(jié)的(13)式是相同的。
因此，基向量矩陣W滿足下式：
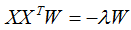
小結(jié)：降維通過樣本數(shù)據(jù)投影到基向量實(shí)現(xiàn)的，基向量的個(gè)數(shù)等于降維的個(gè)數(shù)，基向量是通過上式求解的。
我們知道怎么求解基向量，但是我們事先確定了基向量的個(gè)數(shù)，如上節(jié)的m個(gè)基向量，那么怎么根據(jù)樣本數(shù)據(jù)自動(dòng)的選擇基向量的個(gè)數(shù)了？在回答這一問題前，簡(jiǎn)單闡述下特征向量和特征值的意義。
假設(shè)向量wi，λi分別為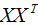
的特征向量和特征值，表達(dá)式如下：
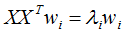
對(duì)應(yīng)的圖：
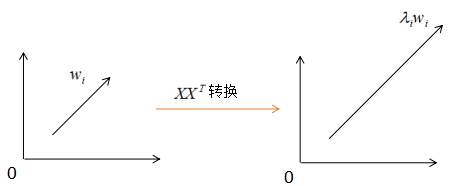
由上圖可知，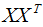
沒有改變特征向量wi的方向，只在wi的方向上伸縮或壓縮了λi倍。特征值代表了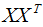在該特征向量的信息分量。特征值越大，包含矩陣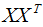的信息分量亦越大。因此，我們可以用λi去選擇基向量個(gè)數(shù)。我們?cè)O(shè)定一個(gè)閾值threshold，該閾值表示降維后的數(shù)據(jù)保留原始數(shù)據(jù)的信息量，假設(shè)降維后的特征個(gè)數(shù)為m，降維前的特征個(gè)數(shù)為n，m應(yīng)滿足下面條件：
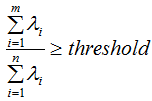
因此，通過上式可以求得基向量的個(gè)數(shù)m，即取前m個(gè)最大特征值對(duì)應(yīng)的基向量?。
投影的基向量：
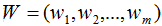
投影的數(shù)據(jù)集：
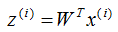
我們?cè)谟?jì)算協(xié)方差矩陣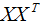
的特征向量前，需要對(duì)樣本數(shù)據(jù)進(jìn)行中心化，中心化的算法如下：
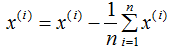
中心化數(shù)據(jù)各特征的平均值為0，計(jì)算過程如下：
對(duì)上式求平均：
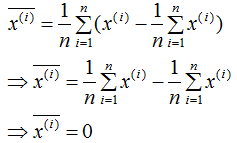
中心化的目的是簡(jiǎn)化算法，我們重新回顧下協(xié)方差矩陣，以說明中心化的作用 。
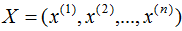，X表示共有n個(gè)樣本數(shù)。
每個(gè)樣本包含n個(gè)特征，即：
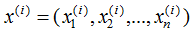
展開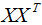
:
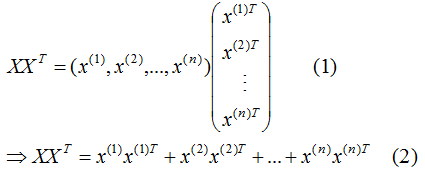
為了閱讀方便，我們只考慮兩個(gè)特征的協(xié)方差矩陣：
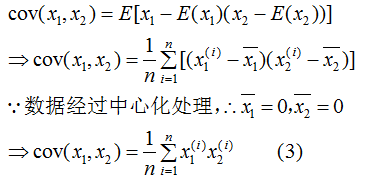
由(3)式推導(dǎo)(2)式得：
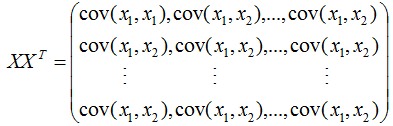
所以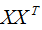
是樣本數(shù)據(jù)的協(xié)方差矩陣，但是，切記必須事先對(duì)數(shù)據(jù)進(jìn)行中心化處理?。
1）樣本數(shù)據(jù)中心化。
2）計(jì)算樣本的協(xié)方差矩陣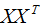
。
3）求協(xié)方差矩陣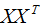的特征值和特征向量，并對(duì)該向量進(jìn)行標(biāo)準(zhǔn)化（基向量）。
3）根據(jù)設(shè)定的閾值，求滿足以下條件的降維數(shù)m。
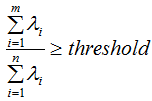
4）取前m個(gè)最大特征值對(duì)應(yīng)的向量，記為W。
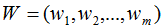
5）對(duì)樣本集的每一個(gè)樣本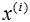
，映射為新的樣本
。
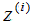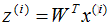
6）得到映射后的樣本集D'。
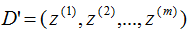
因?yàn)?/span>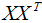
可以用樣本數(shù)據(jù)內(nèi)積表示：
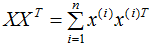
由核函數(shù)定義可知，可通過核函數(shù)將數(shù)據(jù)映射成高維數(shù)據(jù)，并對(duì)該高維數(shù)據(jù)進(jìn)行降維：
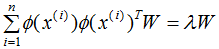
KPCA一般用在數(shù)據(jù)不是線性的，無法直接進(jìn)行PCA降維，需要通過核函數(shù)映射成高維數(shù)據(jù)，再進(jìn)行PCA降維?。
PCA是一種非監(jiān)督學(xué)習(xí)的降維算法，只需要計(jì)算樣本數(shù)據(jù)的協(xié)方差矩陣就能實(shí)現(xiàn)降維的目的，其算法較易實(shí)現(xiàn)，但是降維后特征的可解釋性較弱，且通過降維后信息會(huì)丟失一些，可能對(duì)后續(xù)的處理有重要影響。
參考
https://www.cnblogs.com/pinard/p/6239403.html#undefined
A Singularly Valuable Decompostion: The SVD of a Matrix
交流群
歡迎加入公眾號(hào)讀者群一起和同行交流，目前有SLAM、三維視覺、傳感器、自動(dòng)駕駛、計(jì)算攝影、檢測(cè)、分割、識(shí)別、醫(yī)學(xué)影像、GAN、算法競(jìng)賽等微信群（以后會(huì)逐漸細(xì)分），請(qǐng)掃描下面微信號(hào)加群，備注：”昵稱+學(xué)校/公司+研究方向“，例如：”張三?+?上海交大?+?視覺SLAM“。請(qǐng)按照格式備注，否則不予通過。添加成功后會(huì)根據(jù)研究方向邀請(qǐng)進(jìn)入相關(guān)微信群。請(qǐng)勿在群內(nèi)發(fā)送廣告，否則會(huì)請(qǐng)出群，謝謝理解~