
作者:Adrian Tam, Ray Hong, Jinghan Yu, Brendan Artley
翻譯:汪桉旭
校對:吳振東
轉(zhuǎn)自:數(shù)據(jù)派ID:DatapiTHU
本文約3300字,建議閱讀5分鐘
本文教你了解了如何使用主成分分析來可視化數(shù)據(jù)。
標簽:主成分分析
主成分分析是一種無監(jiān)督的機器學習技術(shù)。可能它最常見的用處就是數(shù)據(jù)的降維。主成分分析除了用于數(shù)據(jù)預(yù)處理,也可以用來可視化數(shù)據(jù)。一圖勝萬言。一旦數(shù)據(jù)可視化,在我們的機器學習模型中就可以更容易得到一些洞見并且決定下一步做什么。在這篇教程中,你將發(fā)現(xiàn)如何使用PCA可視化數(shù)據(jù),并且使用可視化來幫助確定用于降維的參數(shù)。

教程概覽
高維數(shù)據(jù)的散點圖
可視化解釋性方差
前提
在這篇教程學習之前,我們假設(shè)你已經(jīng)熟悉:如何從python中的Scratch計算PCA
Python中用于降維的PCA
高維數(shù)據(jù)的散點圖
可視化是從數(shù)據(jù)中得到洞見的關(guān)鍵一步。我們可以通過可視化學習到一個模式是否可以被觀察到,因此估計哪個機器學習模型是合適的。用二維數(shù)據(jù)描述事物是容易的。正常地,一個有x軸y軸的散點圖就是二維的。用三維數(shù)據(jù)描述事物有一點挑戰(zhàn)性但不是不可能的。例如,在matplotlib中可以繪制三維圖。唯一的問題是在紙面或者屏幕上,我們每次只能從一個角度或者投影來看三維圖。在matplotlib中,視圖由仰角和方位角控制。用四維或者五維數(shù)據(jù)來描述事物是不可能的,因為我們生活在三維世界,并且不知道在這些高維度中數(shù)據(jù)看起來是什么樣的。這就是諸如PCA的數(shù)據(jù)降維技術(shù)發(fā)揮作用的地方。我們可以將數(shù)據(jù)維度降低到二維或者三維以便將其可視化。我們從一個例子開始。我們使用紅酒數(shù)據(jù)集,這個數(shù)據(jù)集是包括13個特征和3種類別的分類數(shù)據(jù)集(也就是說這個數(shù)據(jù)集是13維的)。這里有178個樣本:
在13個特征中,我們可以使用matplotlib挑選任意兩個(我們使用c 參數(shù)對不同的類進行顏色編碼):
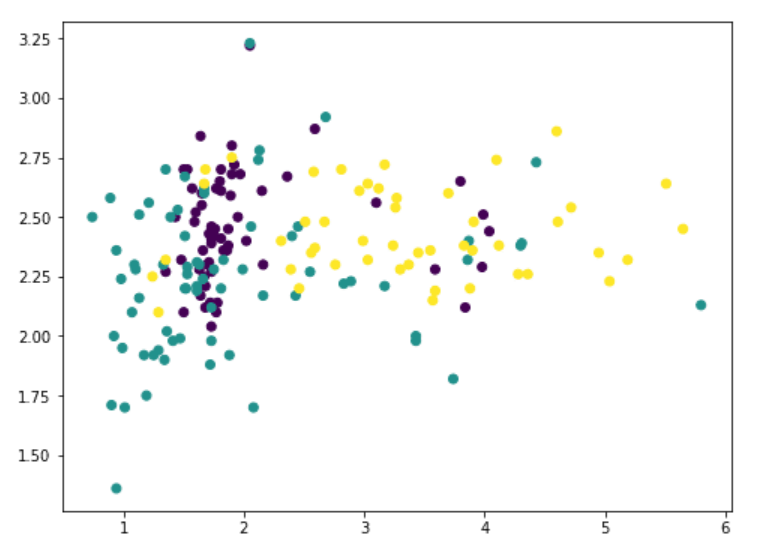

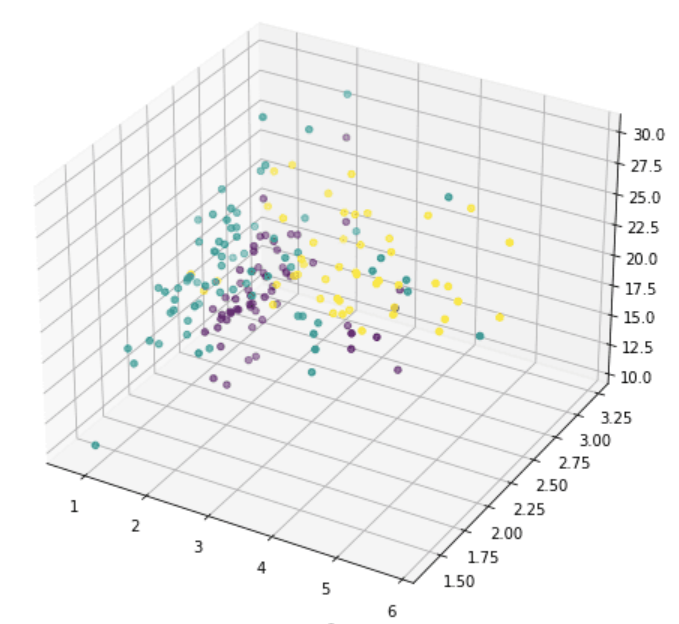
但是這并不能揭示數(shù)據(jù)到底是什么樣,因為大量的特征沒有被展示出來。我們現(xiàn)在轉(zhuǎn)向PCA:
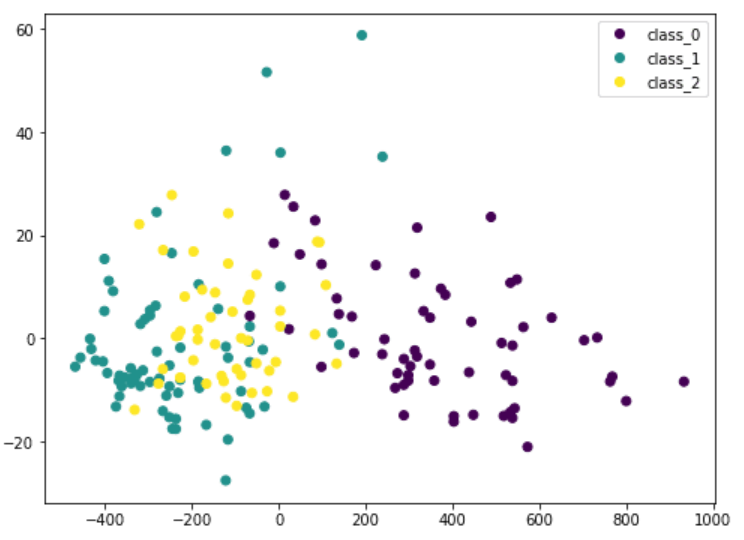
這里我們將輸入數(shù)據(jù)的X通過PCA轉(zhuǎn)換成Xt。我們只考慮包含最重要數(shù)據(jù)的兩欄,并且將其畫成二維圖像。可以看到,紫色類是比較有特色的,但是和其他類存在一些重疊。?如果我們在 PCA 之前縮放數(shù)據(jù)的維度,結(jié)果會有所不同:
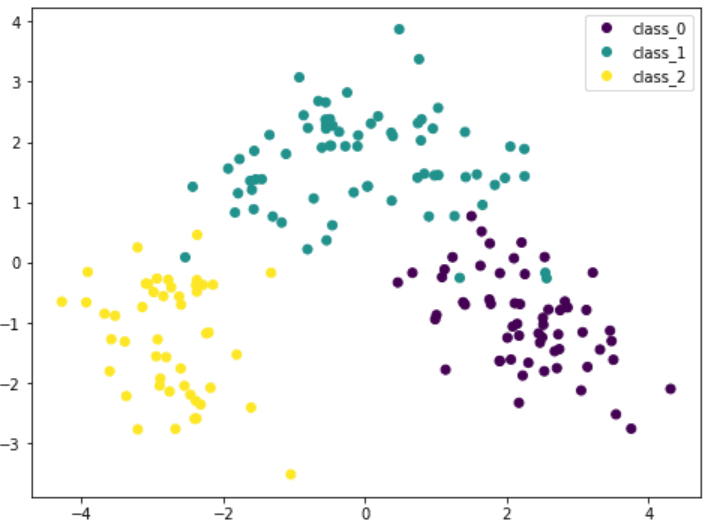
因為 PCA 對數(shù)據(jù)的尺寸很敏感,所以如果通過 StandardScaler 對每個特征進行歸一化,我們可以看到更好的結(jié)果。這樣的話,不同的種類會更有特色性。通過該圖,我們可以確信諸如 SVM 之類的簡單模型可以高精度地對該數(shù)據(jù)集進行分類。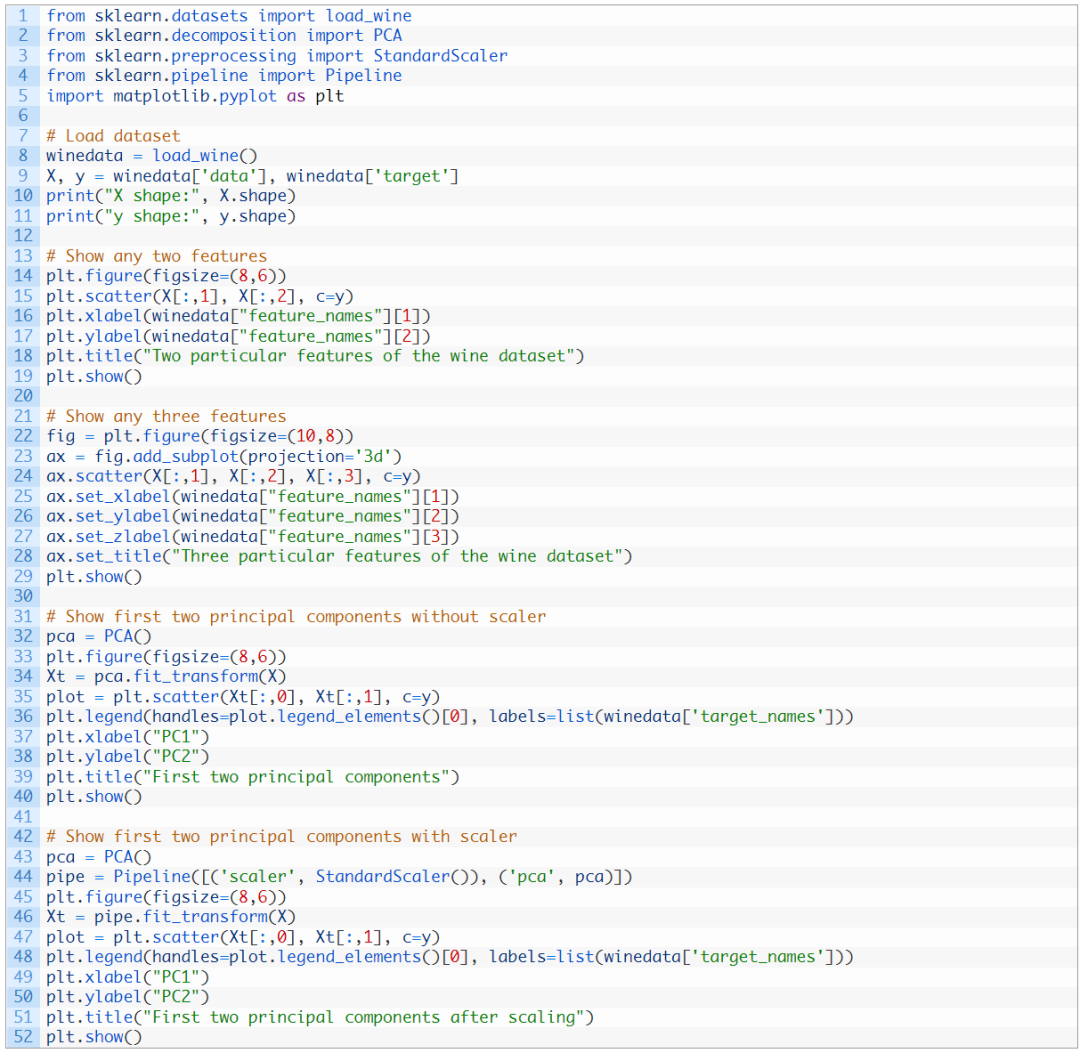
如果我們在不同的數(shù)據(jù)集(例如 MINST 手寫數(shù)字)上應(yīng)用相同的方法,散點圖將不會顯示出明顯的邊界,因此需要更復(fù)雜的模型(例如神經(jīng)網(wǎng)絡(luò))進行分類:
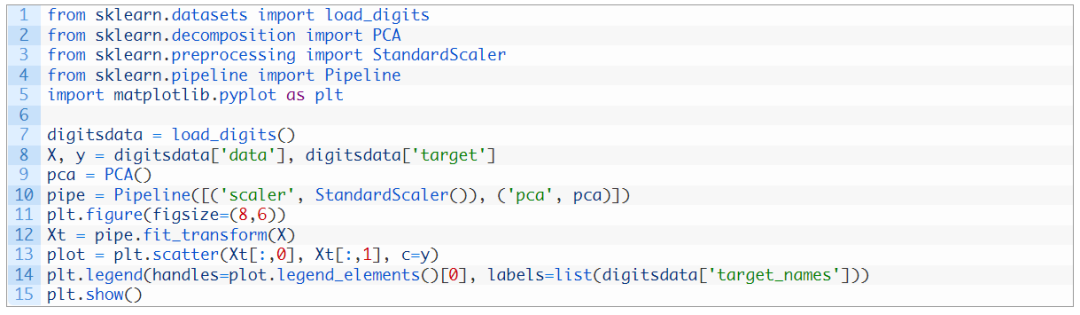
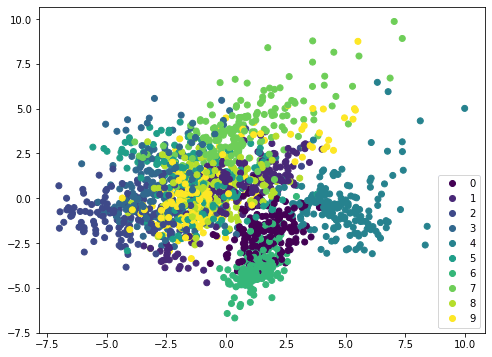
解釋方差可視化
PCA本質(zhì)上是通過特征的線性組合將它們重新排列。因此,它被稱為特征提取技術(shù)。PCA的一個特點是第一個主成分包含有關(guān)數(shù)據(jù)集的最多信息。第二個主成分比第三個主成分提供更多信息,依此類推。為了闡述這個想法,我們可以從原始數(shù)據(jù)集中逐步刪除主成分,然后觀察數(shù)據(jù)集的樣子。?讓我們考慮一個特征較少的數(shù)據(jù)集,并在圖中顯示兩個特征:
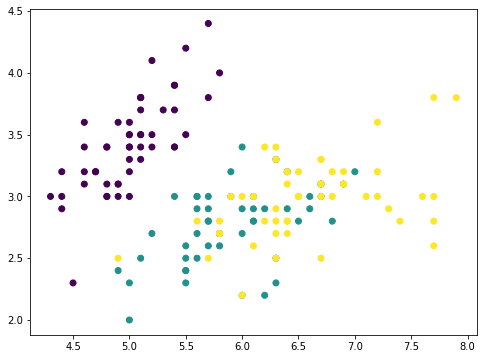
這是只有四個特征的 iris 數(shù)據(jù)集。這些特征具有可比的比例,因此我們可以跳過縮放器。對于一個具有4 個特征的數(shù)據(jù),PCA 最多可以產(chǎn)生 4 個主成分:
例如,第一行是創(chuàng)建第一個主成分的第一個主軸。對于任何具有特征p=(a,b,c,d)的數(shù)據(jù)點p,因為主軸由向量v=(0.36,?0.08,0.86,0.36)表示,所以在主軸上此數(shù)據(jù)點的第一個主成分有值0.36×a–0.08×b+0.86×c+0.36×d。使用向量點乘,此值可以表示為:P?v。因此,將數(shù)據(jù)集X作為一個150×4的矩陣(150個數(shù)據(jù)點,每個數(shù)據(jù)點有4個特征),我們就可以通過矩陣-向量乘法將每個數(shù)據(jù)點映射到該主軸上的值:X?v。計算結(jié)果是長度為150的向量。此時,若我們從每個數(shù)據(jù)點中刪除沿主軸向量的對應(yīng)值,就是:X–(X?v)?vT。其中,轉(zhuǎn)置向量vT是行向量,X?v是列向量,乘積(X?v)?vT遵循矩陣-矩陣乘法法則。計算結(jié)果是一個150×4矩陣,與X維度相同。如果我們繪制(X?v)?vT的前兩個特征,它看起來是這樣:

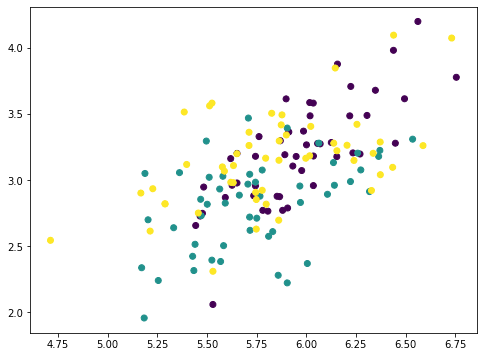
numpy 數(shù)組 Xmean的目的是將X的特征轉(zhuǎn)換到以零為中心,這是 PCA必經(jīng)的一步。然后通過矩陣-向量乘法計算出數(shù)組value 。數(shù)組value是映射在主軸上的每個數(shù)據(jù)點的大小。因此,如果我們將此值乘以主軸向量,得到一個數(shù)組pc1。從原始數(shù)據(jù)集X中刪除它,得到一個新的數(shù)組 Xremove。在圖中,我們觀察到散點圖上的點散落在一起,每個類的聚類都不如之前那么突出。這說明通過刪除第一個主成分,我們刪除了大量信息。如果我們再次重復(fù)相同的過程,這些數(shù)據(jù)點將進一步散落:

這張圖里看起來像一條直線,但實際上不是。如果我們再重復(fù)一遍,所有點會散落成一條直線:

這些點都落在一條直線上,因為我們從數(shù)據(jù)中刪除了三個主成分,而這些數(shù)據(jù)只有四個特征。因此,我們的數(shù)據(jù)矩陣變?yōu)橹葹?的矩陣。你可以嘗試重復(fù)此過程,結(jié)果將是所有點散落成為一個點。在我們刪除主成分時,每個步驟中刪除的信息量可以通過PCA中相應(yīng)的解釋方差比找到:

這里我們可以看到,第一個成分解釋了92.5%的方差,第二個組件解釋了5.3%的方差。如果我們?nèi)サ羟皟蓚€主分量,剩余的方差只有2.2%,因此在視覺上,去掉兩個分量后的圖看起來像一條直線。實際上,當我們檢查上面的圖時,不僅可以看到點被破壞了,而且當我們刪除成分時,x軸和y軸的范圍也更小。在機器學習方面,我們可以考慮在此數(shù)據(jù)集中僅使用一個特征進行分類,即第一個主成分。相比使用全部特征得到的原始準確度,此時獲得的準確度有望不低于它原來的90%: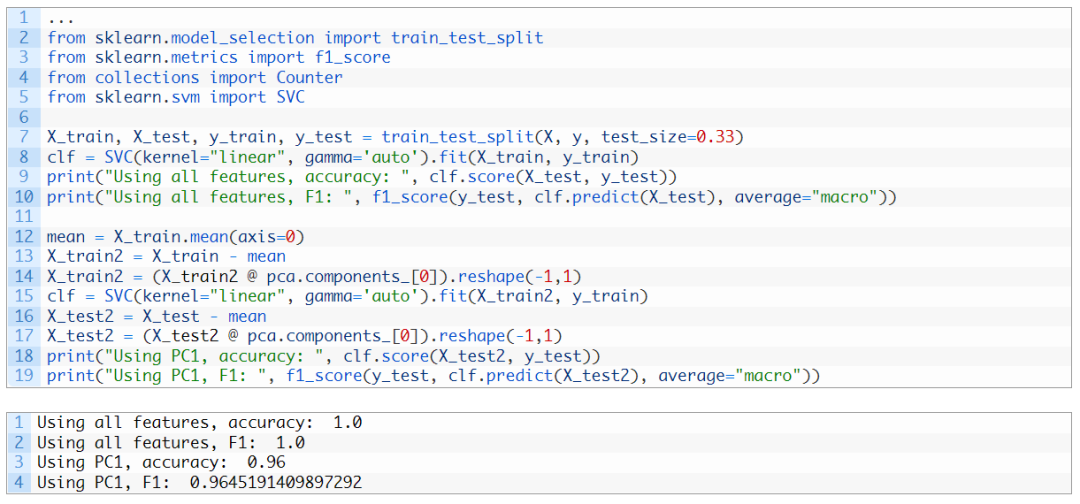

解釋方差的另一個用途在于壓縮。鑒于第一個主分量的解釋方差很大,如果我們需要存儲數(shù)據(jù)集,我們只能存儲第一個主軸上的投影值(X?v)以及向量v的主軸。然后,我們可以通過乘以原始數(shù)據(jù)集來近似地重現(xiàn)它們:X≈(X?v)?vT。通過這種方式,我們只需要存儲每個數(shù)據(jù)點的一個值,而不是四個特征的四個值。如果我們將投影值存儲在多個主軸上并將多個主成分相加,則近似值會更準確。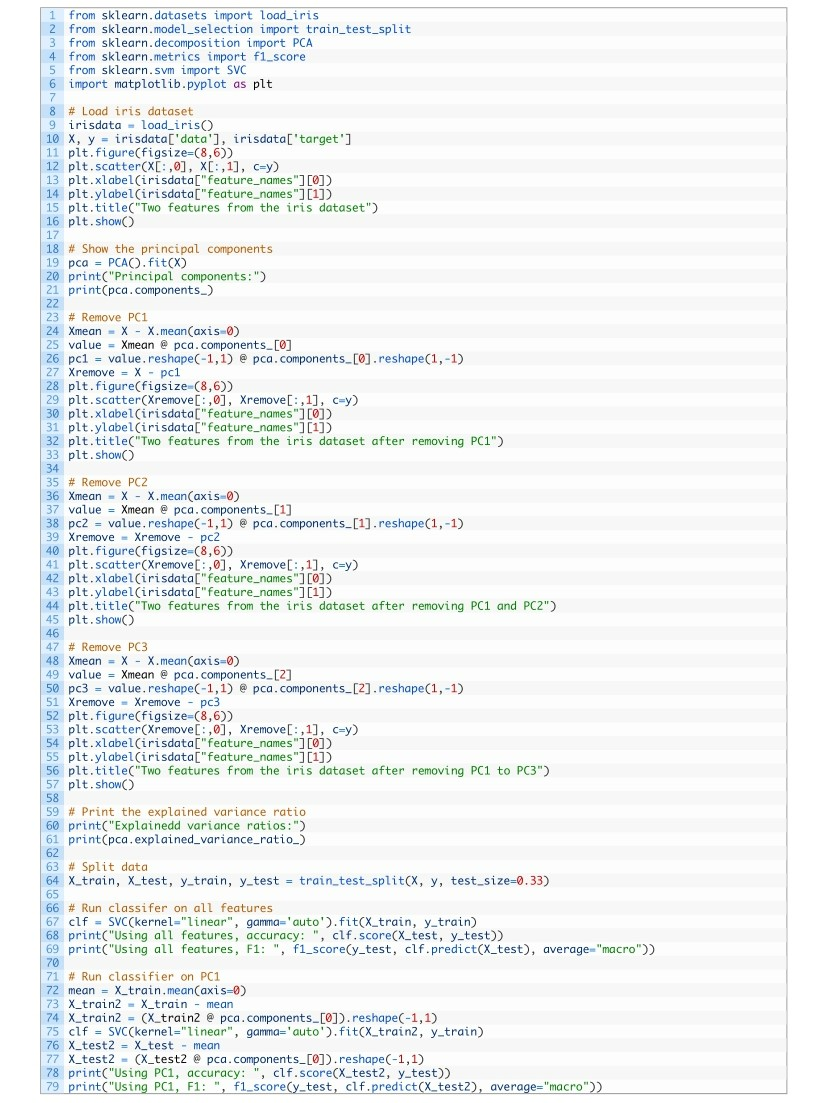
拓展閱讀
書籍
https://amzn.to/3qSk3C2
教程
https://machinelearningmastery.com/calculate-principal-component-analysis-scratch-python/
https://machinelearningmastery.com/principal-components-analysis-for-dimensionality-reduction-in-python/
APIs
scikit-learn toy datasets?https://scikit-learn.org/stable/datasets/toy_dataset.htmlscikit-learn iris datasethttps://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_iris.htmlscikit-learn wine datasethttps://scikit-?learn.org/stable/modules/generated/sklearn.datasets.load_wine.htmlhttps://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.scatter.htmlhttps://matplotlib.org/stable/tutorials/toolkits/mplot3d.html總結(jié)
在本教程中,你了解了如何使用主成分分析來可視化數(shù)據(jù)。汪桉旭,南京航空航天大學研究生。對數(shù)據(jù)科學充滿興趣,熱衷于在分享中提高自己,在實踐中學習新知識。休閑時間喜歡看電影看小說。樂于結(jié)交新朋友、一起探索新愛好。。




























