貝葉斯網(wǎng)絡(luò)，看完這篇我終于理解了！

1. 對(duì)概率圖模型的理解

2. 細(xì)數(shù)貝葉斯網(wǎng)絡(luò)

2.1 頻率派觀點(diǎn)

2.2 貝葉斯學(xué)派

• 頻率派把需要推斷的參數(shù)θ看做是固定的未知常數(shù)，即概率雖然是未知的，但最起碼是確定的一個(gè)值，同時(shí)，樣本X 是隨機(jī)的，所以頻率派重點(diǎn)研究樣本空間，大部分的概率計(jì)算都是針對(duì)樣本X 的分布；
• 而貝葉斯派的觀點(diǎn)則截然相反，他們認(rèn)為參數(shù)是隨機(jī)變量，而樣本X 是固定的，由于樣本是固定的，所以他們重點(diǎn)研究的是參數(shù)的分布。

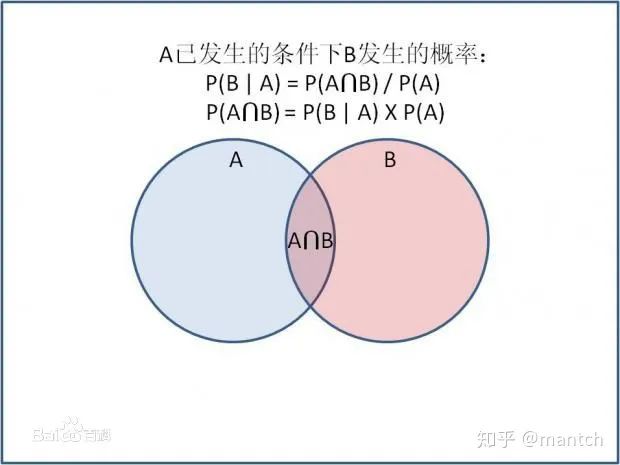
2.3 貝葉斯定理

聯(lián)合概率：

邊緣概率(先驗(yàn)概率)：P(A)或者P(B)

2.4 貝葉斯網(wǎng)絡(luò)

貝葉斯網(wǎng)絡(luò)的有向無環(huán)圖中的節(jié)點(diǎn)表示隨機(jī)變量

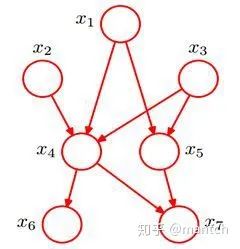
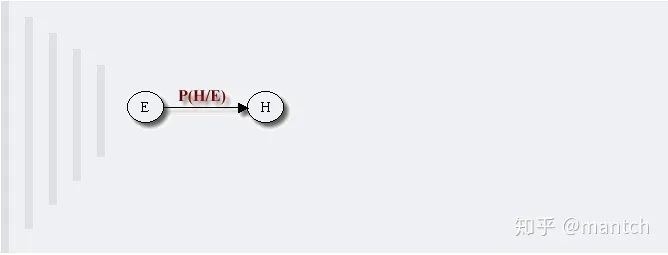
2.4.1 貝葉斯網(wǎng)絡(luò)的結(jié)構(gòu)形式

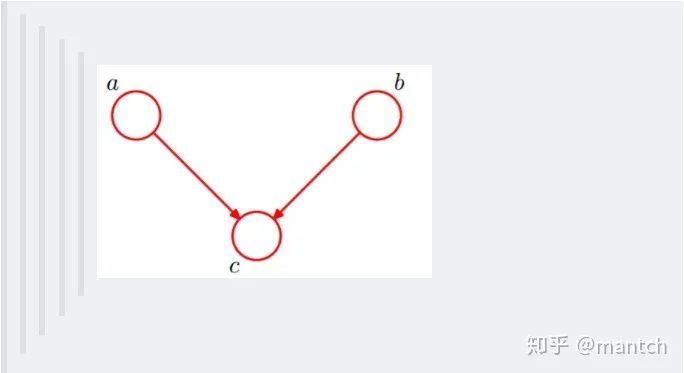
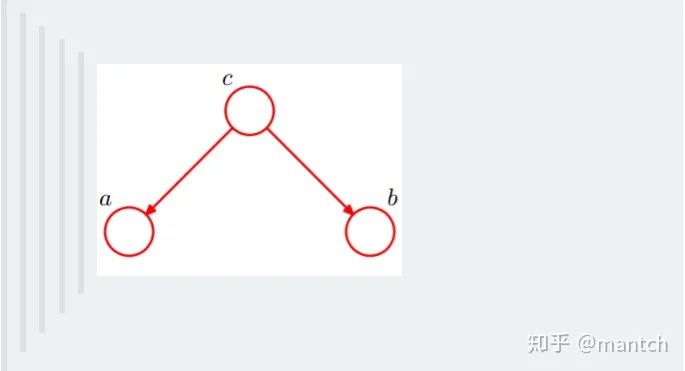
1. 在c未知的時(shí)候，有：P(a,b,c)=P(c)_P(a|c)_P(b|c)，此時(shí)，沒法得出P(a,b) = P(a)P(b)，即c未知時(shí)，a、b不獨(dú)立。
2. 在c已知的時(shí)候，有：P(a,b|c)=P(a,b,c)/P(c)，然后將P(a,b,c)=P(c)_P(a|c)_P(b|c)帶入式子中，得到：P(a,b|c)=P(a,b,c)/P(c) = P(c)_P(a|c)_P(b|c) / P(c) = P(a|c)*P(b|c)，即c已知時(shí)，a、b獨(dú)立。

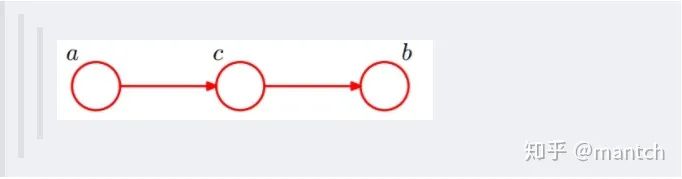
1. c未知時(shí)，有：P(a,b,c)=P(a)_P(c|a)_P(b|c)，但無法推出P(a,b) = P(a)P(b)，即c未知時(shí)，a、b不獨(dú)立。
2. c已知時(shí)，有：P(a,b|c)=P(a,b,c)/P(c)，且根據(jù)P(a,c) = P(a)_P(c|a) = P(c)_P(a|c)，可化簡(jiǎn)得到：

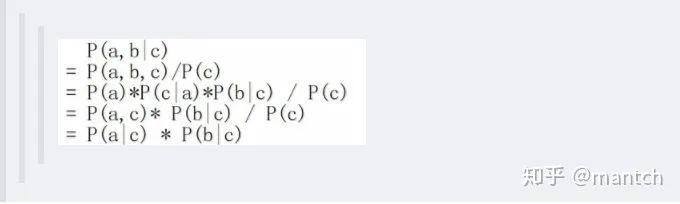
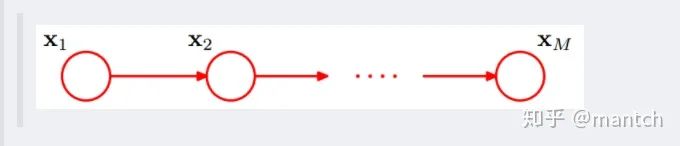
2.4.2 因子圖

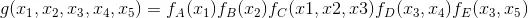
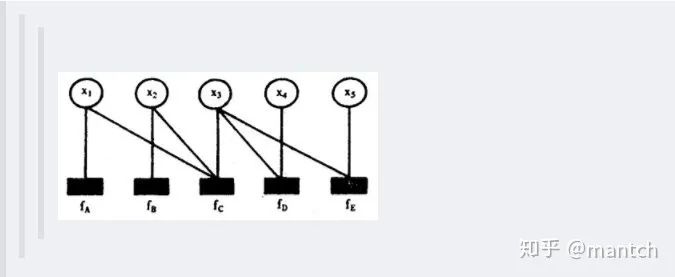
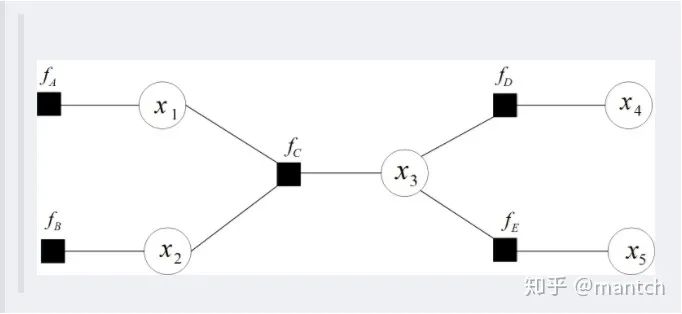
2.5 樸素貝葉斯

• 一個(gè)特征出現(xiàn)的概率與其他特征（條件）獨(dú)立；
• 每個(gè)特征同等重要。

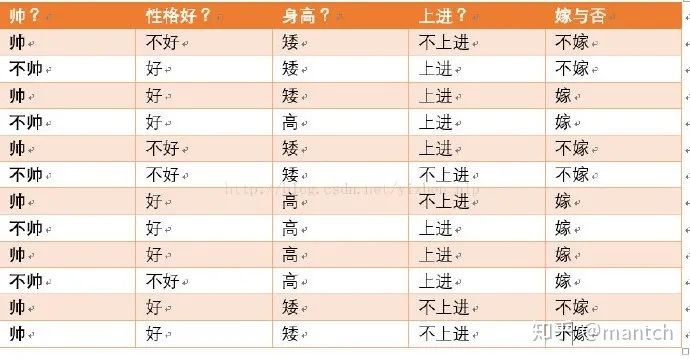
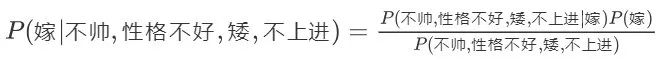
1. 我們這么想，假如沒有這個(gè)假設(shè)，那么我們對(duì)右邊這些概率的估計(jì)其實(shí)是不可做的，這么說，我們這個(gè)例子有4個(gè)特征，其中帥包括{帥，不帥}，性格包括{不好，好，爆好}，身高包括{高，矮，中}，上進(jìn)包括{不上進(jìn)，上進(jìn)}，那么四個(gè)特征的聯(lián)合概率分布總共是4維空間，總個(gè)數(shù)為2_3_3*2=36個(gè)。
   36個(gè)，計(jì)算機(jī)掃描統(tǒng)計(jì)還可以，但是現(xiàn)實(shí)生活中，往往有非常多的特征，每一個(gè)特征的取值也是非常之多，那么通過統(tǒng)計(jì)來估計(jì)后面概率的值，變得幾乎不可做，這也是為什么需要假設(shè)特征之間獨(dú)立的原因。
2. 假如我們沒有假設(shè)特征之間相互獨(dú)立，那么我們統(tǒng)計(jì)的時(shí)候，就需要在整個(gè)特征空間中去找，比如統(tǒng)計(jì)p(不帥、性格不好、身高矮、不上進(jìn)|嫁),我們就需要在嫁的條件下，去找四種特征全滿足分別是不帥，性格不好，身高矮，不上進(jìn)的人的個(gè)數(shù)，這樣的話，由于數(shù)據(jù)的稀疏性，很容易統(tǒng)計(jì)到0的情況。這樣是不合適的。

• 算法邏輯簡(jiǎn)單,易于實(shí)現(xiàn)（算法思路很簡(jiǎn)單，只要使用貝葉斯公式轉(zhuǎn)化即可！）
• 分類過程中時(shí)空開銷小（假設(shè)特征相互獨(dú)立，只會(huì)涉及到二維存儲(chǔ)）

3. 基于貝葉斯的一些問題

1. 解釋樸素貝葉斯算法里面的先驗(yàn)概率、似然估計(jì)和邊際似然估計(jì)？

• 先驗(yàn)概率： 就是因變量（二分法）在數(shù)據(jù)集中的比例。這是在你沒有任何進(jìn)一步的信息的時(shí)候，是對(duì)分類能做出的最接近的猜測(cè)。
• 似然估計(jì)： 似然估計(jì)是在其他一些變量的給定的情況下，一個(gè)觀測(cè)值被分類為1的概率。例如，“FREE”這個(gè)詞在以前的垃圾郵件使用的概率就是似然估計(jì)。
• 邊際似然估計(jì)： 邊際似然估計(jì)就是，“FREE”這個(gè)詞在任何消息中使用的概率。

4. 生成式模型和判別式模型的區(qū)別

• 判別模型 (discriminative model)通過求解條件概率分布P(y|x)或者直接計(jì)算y的值來預(yù)測(cè)y。
  線性回歸（Linear Regression）,邏輯回歸（Logistic Regression）,支持向量機(jī)（SVM）, 傳統(tǒng)神經(jīng)網(wǎng)絡(luò)（Traditional Neural Networks）,線性判別分析（Linear Discriminative Analysis），條件隨機(jī)場(chǎng)（Conditional Random Field）
• 生成模型（generative model）通過對(duì)觀測(cè)值和標(biāo)注數(shù)據(jù)計(jì)算聯(lián)合概率分布P(x,y)來達(dá)到判定估算y的目的。
  樸素貝葉斯（Naive Bayes）, 隱馬爾科夫模型（HMM）,貝葉斯網(wǎng)絡(luò)（Bayesian Networks）和隱含狄利克雷分布（Latent Dirichlet Allocation）、混合高斯模型

5. 代碼實(shí)現(xiàn)

6. 參考文獻(xiàn)

作者：@mantchs（https://github.com/NLP-LOVE/ML-NLP）
GitHub：https://github.com/NLP-LOVE/ML-NLP