基于梯度下降算法求解線性回歸

點(diǎn)擊上方“小白學(xué)視覺(jué)”，選擇加"星標(biāo)"或“置頂”

重磅干貨，第一時(shí)間送達(dá)

01. 線性回歸(Linear Regression)

梯度下降算法在機(jī)器學(xué)習(xí)方法分類中屬于監(jiān)督學(xué)習(xí)。利用它可以求解線性回歸問(wèn)題，計(jì)算一組二維數(shù)據(jù)之間的線性關(guān)系，假設(shè)有一組數(shù)據(jù)如下下圖所示

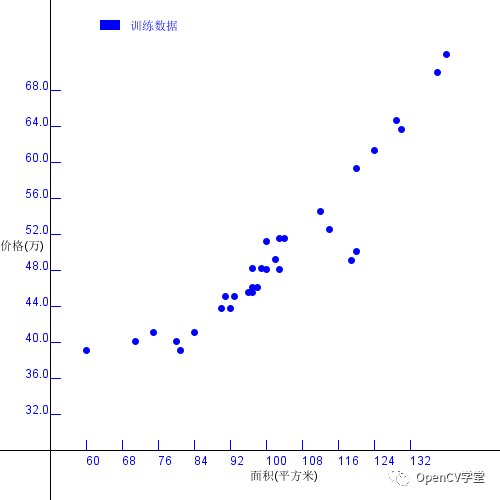
其中X軸方向表示房屋面積、Y軸表示房屋價(jià)格。我們希望根據(jù)上述的數(shù)據(jù)點(diǎn)，擬合出一條直線，能跟對(duì)任意給定的房屋面積實(shí)現(xiàn)價(jià)格預(yù)言，這樣求解得到直線方程過(guò)程就叫線性回歸，得到的直線為回歸直線，數(shù)學(xué)公式表示如下:

02. 梯度下降

 

03. 代碼實(shí)現(xiàn)各步

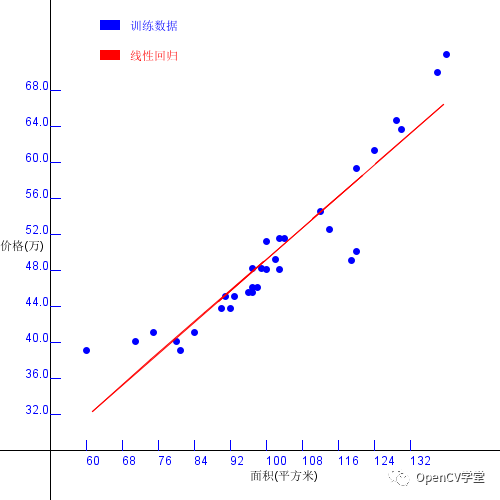
訓(xùn)練數(shù)據(jù)讀入

List<DataItem> items = new ArrayList<DataItem>();
File f = new File(fileName);
try {
    if (f.exists()) {
        BufferedReader br = new BufferedReader(new FileReader(f));
        String line = null;
        while((line = br.readLine()) != null) {
            String[] data = line.split(",");
            if(data != null && data.length == 2) {
                DataItem item = new DataItem();
                item.x = Integer.parseInt(data[0]);
                item.y = Integer.parseInt(data[1]);
                items.add(item);
            }
        }
        br.close();
    }
} catch (IOException ioe) {
    System.err.println(ioe);
}
return items;

歸一化處理

float min = 100000;
float max = 0;
for(DataItem item : items) {
    min = Math.min(min, item.x);
    max = Math.max(max, item.x);
}
float delta = max - min;
for(DataItem item : items) {
    item.x = (item.x - min) / delta;
}

梯度下降

int repetion = 1500;
float learningRate = 0.1f;
float[] theta = new float[2];
Arrays.fill(theta, 0);
float[] hmatrix = new float[items.size()];
Arrays.fill(hmatrix, 0);
int k=0;
float s1 = 1.0f / items.size();
float sum1=0, sum2=0;
for(int i=0; i<repetion; i++) {
    for(k=0; k<items.size(); k++ ) {
        hmatrix[k] = ((theta[0] + theta[1]*items.get(k).x) - items.get(k).y);
    }
    for(k=0; k<items.size(); k++ ) {
        sum1 += hmatrix[k];
        sum2 += hmatrix[k]*items.get(k).x;
    }
    sum1 = learningRate*s1*sum1;
    sum2 = learningRate*s1*sum2;
    // 更新 參數(shù)theta
    theta[0] = theta[0] - sum1;
    theta[1] = theta[1] - sum2;
}
return theta;

價(jià)格預(yù)言 - theta表示參數(shù)矩陣

float result = theta[0] + theta[1]*input;
return result;

線性回歸Plot繪制

int w = 500;
int h = 500;
BufferedImage plot = new BufferedImage(w, h, BufferedImage.TYPE_INT_ARGB);
Graphics2D g2d = plot.createGraphics();
g2d.setRenderingHint(RenderingHints.KEY_ANTIALIASING, RenderingHints.VALUE_ANTIALIAS_ON);
g2d.setPaint(Color.WHITE);
g2d.fillRect(0, 0, w, h);
g2d.setPaint(Color.BLACK);
int margin = 50;
g2d.drawLine(margin, 0, margin, h);
g2d.drawLine(0, h-margin, w, h-margin);
float minx=Float.MAX_VALUE, maxx=Float.MIN_VALUE;
float miny=Float.MAX_VALUE, maxy=Float.MIN_VALUE;
for(DataItem item : series1) {
    minx = Math.min(item.x, minx);
    maxx = Math.max(maxx, item.x);
    miny = Math.min(item.y, miny);
    maxy = Math.max(item.y, maxy);
}
for(DataItem item : series2) {
    minx = Math.min(item.x, minx);
    maxx = Math.max(maxx, item.x);
    miny = Math.min(item.y, miny);
    maxy = Math.max(item.y, maxy);
}
// draw X, Y Title and Aixes
g2d.setPaint(Color.BLACK);
g2d.drawString("價(jià)格(萬(wàn))", 0, h/2);
g2d.drawString("面積(平方米)", w/2, h-20);
// draw labels and legend
g2d.setPaint(Color.BLUE);
float xdelta = maxx - minx;
float ydelta = maxy - miny;
float xstep = xdelta / 10.0f;
float ystep = ydelta / 10.0f;
int dx = (w - 2*margin) / 11;
int dy = (h - 2*margin) / 11;
// draw labels
for(int i=1; i<11; i++) {
    g2d.drawLine(margin+i*dx, h-margin, margin+i*dx, h-margin-10);
    g2d.drawLine(margin, h-margin-dy*i, margin+10, h-margin-dy*i);
    int xv = (int)(minx + (i-1)*xstep);
    float yv = (int)((miny + (i-1)*ystep)/10000.0f);
    g2d.drawString(""+xv, margin+i*dx, h-margin+15);
    g2d.drawString(""+yv, margin-25, h-margin-dy*i);
}
// draw point
g2d.setPaint(Color.BLUE);
for(DataItem item : series1) {
    float xs = (item.x - minx) / xstep + 1;
    float ys = (item.y - miny) / ystep + 1;
    g2d.fillOval((int)(xs*dx+margin-3), (int)(h-margin-ys*dy-3), 7,7);
}
g2d.fillRect(100, 20, 20, 10);
g2d.drawString("訓(xùn)練數(shù)據(jù)", 130, 30);
// draw regression line
g2d.setPaint(Color.RED);
for(int i=0; i<series2.size()-1; i++) {
    float x1 = (series2.get(i).x - minx) / xstep + 1;
    float y1 = (series2.get(i).y - miny) / ystep + 1;
    float x2 = (series2.get(i+1).x - minx) / xstep + 1;
    float y2 = (series2.get(i+1).y - miny) / ystep + 1;
    g2d.drawLine((int)(x1*dx+margin-3), (int)(h-margin-y1*dy-3), (int)(x2*dx+margin-3), (int)(h-margin-y2*dy-3));
}
g2d.fillRect(100, 50, 20, 10);
g2d.drawString("線性回歸", 130, 60);
g2d.dispose();
saveImage(plot);

04. 總結(jié)

本文通過(guò)最簡(jiǎn)單的示例，演示了利用梯度下降算法實(shí)現(xiàn)線性回歸分析，使用更新收斂的算法常被稱為L(zhǎng)MS(Least Mean Square)又叫Widrow-Hoff學(xué)習(xí)規(guī)則，此外梯度下降算法還可以進(jìn)一步區(qū)分為增量梯度下降算法與批量梯度下降算法，這兩種梯度下降方法在基于神經(jīng)網(wǎng)絡(luò)的機(jī)器學(xué)習(xí)中經(jīng)常會(huì)被提及，對(duì)此感興趣的可以自己進(jìn)一步探索與研究。

下載1：OpenCV-Contrib擴(kuò)展模塊中文版教程

在「小白學(xué)視覺(jué)」公眾號(hào)后臺(tái)回復(fù)：擴(kuò)展模塊中文教程，即可下載全網(wǎng)第一份OpenCV擴(kuò)展模塊教程中文版，涵蓋擴(kuò)展模塊安裝、SFM算法、立體視覺(jué)、目標(biāo)跟蹤、生物視覺(jué)、超分辨率處理等二十多章內(nèi)容。

下載2：Python視覺(jué)實(shí)戰(zhàn)項(xiàng)目52講

在「小白學(xué)視覺(jué)」公眾號(hào)后臺(tái)回復(fù)：Python視覺(jué)實(shí)戰(zhàn)項(xiàng)目，即可下載包括圖像分割、口罩檢測(cè)、車道線檢測(cè)、車輛計(jì)數(shù)、添加眼線、車牌識(shí)別、字符識(shí)別、情緒檢測(cè)、文本內(nèi)容提取、面部識(shí)別等31個(gè)視覺(jué)實(shí)戰(zhàn)項(xiàng)目，助力快速學(xué)校計(jì)算機(jī)視覺(jué)。

下載3：OpenCV實(shí)戰(zhàn)項(xiàng)目20講

在「小白學(xué)視覺(jué)」公眾號(hào)后臺(tái)回復(fù)：OpenCV實(shí)戰(zhàn)項(xiàng)目20講，即可下載含有20個(gè)基于OpenCV實(shí)現(xiàn)20個(gè)實(shí)戰(zhàn)項(xiàng)目，實(shí)現(xiàn)OpenCV學(xué)習(xí)進(jìn)階。

交流群

歡迎加入公眾號(hào)讀者群一起和同行交流，目前有SLAM、三維視覺(jué)、傳感器、自動(dòng)駕駛、計(jì)算攝影、檢測(cè)、分割、識(shí)別、醫(yī)學(xué)影像、GAN、算法競(jìng)賽等微信群（以后會(huì)逐漸細(xì)分），請(qǐng)掃描下面微信號(hào)加群，備注：”昵稱+學(xué)校/公司+研究方向“，例如：”張三 + 上海交大 + 視覺(jué)SLAM“。請(qǐng)按照格式備注，否則不予通過(guò)。添加成功后會(huì)根據(jù)研究方向邀請(qǐng)進(jìn)入相關(guān)微信群。請(qǐng)勿在群內(nèi)發(fā)送廣告，否則會(huì)請(qǐng)出群，謝謝理解~