【深度學(xué)習(xí)】PyTorch 中的線性回歸和梯度下降
我們正在使用 Jupyter notebook 來運行我們的代碼。我們建議在Google Colaboratory上遵循本教程。你可以查看此鏈接以獲取有關(guān)其用法的更多信息。
https://www.analyticsvidhya.com/blog/2020/03/google-colab-machine-learning-deep-learning/
為了完成本教程,假設(shè)你已具備 PyTorch 和 Python 編程的先驗知識。不需要機器學(xué)習(xí)的先決知識。你可以查看我們之前關(guān)于 PyTorch 的博客以熟悉它。
https://www.analyticsvidhya.com/blog/2021/04/a-gentle-introduction-to-pytorch-library/
線性回歸簡介
反向傳播是深度學(xué)習(xí)中一種強大的技術(shù),用于更新權(quán)重和偏差,從而使模型能夠?qū)W習(xí)。為了更好地說明反向傳播,讓我們看一下線性回歸模型在 PyTorch 中的實現(xiàn)
線性回歸是機器學(xué)習(xí)中的基本算法之一。線性回歸在輸入特征 (X) 和輸出標(biāo)簽 (y) 之間建立線性關(guān)系。
在線性回歸中,每個輸出標(biāo)簽都表示為使用權(quán)重和偏差的輸入特征的線性函數(shù)。這些權(quán)重和偏差是隨機初始化的模型參數(shù),然后通過數(shù)據(jù)集的每個訓(xùn)練/學(xué)習(xí)周期進行更新。在經(jīng)過一次訓(xùn)練數(shù)據(jù)迭代后訓(xùn)練模型和更新參數(shù)被稱為一個時期。
所以現(xiàn)在我們應(yīng)該訓(xùn)練模型幾個時期,以便權(quán)重和偏差可以學(xué)習(xí)輸入特征和輸出標(biāo)簽之間的線性關(guān)系。
因此,在本教程中,讓我們創(chuàng)建一個假設(shè)數(shù)據(jù)模型,該模型由芒果和橙子的作物產(chǎn)量組成,并給出了特定地點的平均溫度、年降雨量和濕度。訓(xùn)練數(shù)據(jù)如下:
| 地區(qū) | 溫度(華氏度) | 降雨量(毫米) | 濕度 (%) | 芒果(噸) | 橙子(噸) |
|---|---|---|---|---|---|
| A | 73 | 67 | 43 | 56 | 70 |
| B | 91 | 88 | 64 | 81 | 101 |
| C | 87 | 134 | 58 | 119 | 133 |
| D | 102 | 43 | 37 | 22 | 37 |
| E | 69 | 96 | 70 | 103 | 119 |
| F | 74 | 66 | 43 | 57 | 69 |
| G | 91 | 87 | 65 | 80 | 102 |
| H | 88 | 134 | 59 | 118 | 132 |
| I | 101 | 44 | 37 | 21 | 38 |
| J | 68 | 96 | 71 | 104 | 118 |
| 鉀 | 73 | 66 | 44 | 57 | 69 |
| 升 | 92 | 87 | 64 | 82 | 100 |
| 米 | 87 | 135 | 57 | 118 | 134 |
| N | 103 | 43 | 36 | 20 | 38 |
| 哦 | 68 | 97 | 70 | 102 | 120 |
在線性回歸中,每個目標(biāo)標(biāo)簽都表示為輸入變量的加權(quán)總和以及偏差,即
芒果 = w11 * 溫度 + w 12 * 降雨量 + w 13 * 濕度 + b 1
橙子 = w 21 * 溫度 + w 22 * 降雨量 + w 23 * 濕度 + b 2
最初,權(quán)重和偏差是隨機初始化的,然后在訓(xùn)練過程中進行相應(yīng)的更新,以便這些權(quán)重和偏差能夠預(yù)測任何地區(qū)的芒果和橙子產(chǎn)量,前提是溫度、降雨量和濕度達到一定的準(zhǔn)確度。
簡而言之,這就是機器學(xué)習(xí)。
所以現(xiàn)在讓我們開始使用 Pytorch 實現(xiàn)
進口
導(dǎo)入所需的庫
import?torch
import?numpy?as?np
加載數(shù)據(jù)
上表中給出的訓(xùn)練數(shù)據(jù)可以使用 NumPy 表示為矩陣。所以讓我們分別定義輸入和目標(biāo),
inputs?=?np.array([[73,?67,?43],?
???????????????????[91,?88,?64],?
???????????????????[87,?134,?58],?
???????????????????[102,?43,?37],?
???????????????????[69,?96,?70],?
???????????????????[74,?66,?43],?
???????????????????[91,?87,?65],?
???????????????????[88,?134,?59],?
???????????????????[101,?44,?37],?
???????????????????[68,?96,?71],?
???????????????????[73,?66,?44],?
???????????????????[92,?87,?64],?
???????????????????[87,?135,?57],?
???????????????????[103,?43,?36],?
???????????????????[68,?97,?70]],?
??????????????????dtype='float32')
targets?=?np.array([[56,?70],?
????????????????????[81,?101],?
????????????????????[119,?133],?
????????????????????[22,?37],?
????????????????????[103,?119],
????????????????????[57,?69],?
????????????????????[80,?102],?
????????????????????[118,?132],?
????????????????????[21,?38],?
????????????????????[104,?118],?
????????????????????[57,?69],?
????????????????????[82,?100],?
????????????????????[118,?134],?
????????????????????[20,?38],?
????????????????????[102,?120]],?
???????????????????dtype='float32')
輸入矩陣和目標(biāo)矩陣都作為 NumPy 數(shù)組加載。
這應(yīng)該使用torch.from_numpy()方法轉(zhuǎn)換為torch張量 ,
inputs?=?torch.from_numpy(inputs)
targets?=?torch.from_numpy(targets)
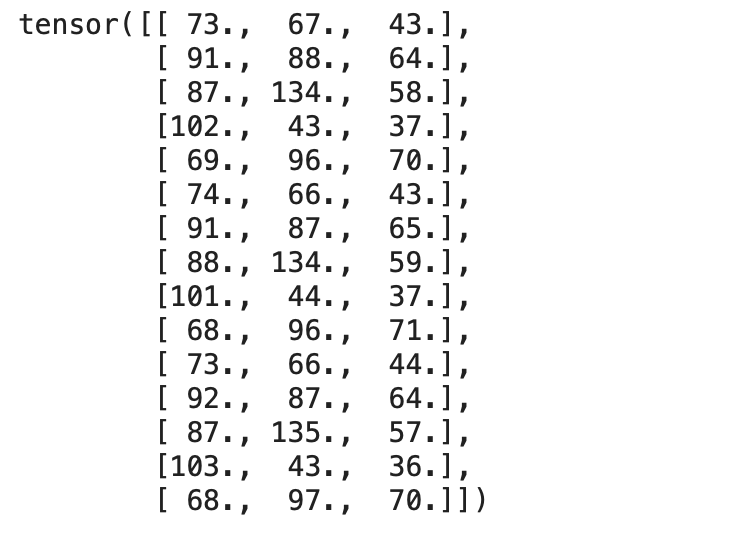
我們可以檢查兩個張量,
print(inputs)
輸出:
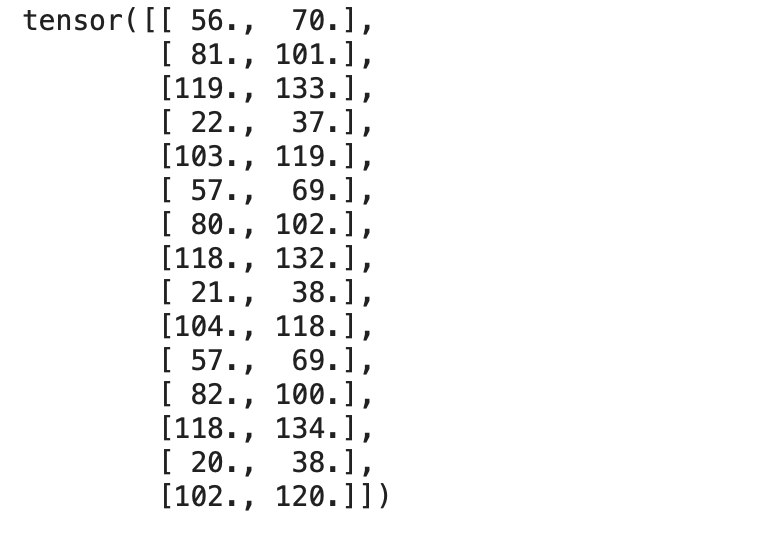
print(targets)
輸出:
現(xiàn)在讓我們創(chuàng)建一個TensorDataset,它將輸入和目標(biāo)張量包裝到一個數(shù)據(jù)集中。讓我們從torch.utils.data導(dǎo)入TensorDataset方法。
我們可以以元組的形式訪問數(shù)據(jù)集中的行。
from?torch.utils.data?import?TensorDataset
dataset?=?TensorDataset(inputs,?targets)
我們可以使用 Python 中的索引從定義的數(shù)據(jù)集中訪問輸入行和相應(yīng)的目標(biāo)。
dataset[:3]

現(xiàn)在讓我們將數(shù)據(jù)集轉(zhuǎn)換為數(shù)據(jù)加載器,它可以在訓(xùn)練期間將數(shù)據(jù)拆分為預(yù)定義批量大小的批次。
使用 Pytorch 的DataLoader類,我們可以將數(shù)據(jù)集轉(zhuǎn)換為預(yù)定義批量大小的批次,并通過從數(shù)據(jù)集中隨機挑選樣本來創(chuàng)建批次。
from?torch.utils.data?import?DataLoader
batch_size?=?3
train_loader?=?DataLoader(dataset,?batch_size=batch_size,?shuffle=True)
我們可以使用 for 循環(huán)將DataLoader 中的數(shù)據(jù)作為包含輸入和相應(yīng)目標(biāo)的元組對訪問,這使我們能夠?qū)⑴沃苯蛹虞d到訓(xùn)練循環(huán)中。
#?A?Batch?Sample
for?inp,target?in?train_loader:
????print(inp)
????print(target)
????break
輸出:

現(xiàn)在我們的數(shù)據(jù)已準(zhǔn)備好進行訓(xùn)練,讓我們定義線性回歸算法。
線性回歸——從頭開始
在統(tǒng)計建模中,回歸分析是一組統(tǒng)計過程,用于估計因變量與一個或多個自變量之間的關(guān)系。-維基百科
讓我們從頭開始實現(xiàn)一個線性回歸模型。我們應(yīng)該找到上述方程中指定的最佳權(quán)重和偏差,以便它定義輸入和輸出之間的理想線性關(guān)系。
因此,我們定義了一組權(quán)重,如上述等式,以建立與輸入特征和目標(biāo)的線性關(guān)系。在這里,我們還將超參數(shù)(即權(quán)重和偏差)的requires_grad屬性設(shè)置 為True。
w?=?torch.randn(2,?3,?requires_grad=True)
b?=?torch.randn(2,?requires_grad=True)
print(w)
print(b)
輸出:

torch.randn從均值 0 和標(biāo)準(zhǔn)差 1 的均勻分布中隨機生成張量。
線性回歸方程為 y = w * X + b,其中
y是輸出或因變量
X是輸入或自變量
w & b分別是權(quán)重和偏差
因此,現(xiàn)在讓我們定義我們的線性回歸模型,
def?model(X):
????return?X?@?w.t()?+?b
該模型只是一個建立權(quán)重和輸出之間線性關(guān)系的數(shù)學(xué)方程。
使用輸入批次和權(quán)重的轉(zhuǎn)置執(zhí)行矩陣乘法(@ 表示矩陣乘法)。
現(xiàn)在讓我們?yōu)橐慌鷶?shù)據(jù)預(yù)測模型的輸出,
for?x,y?in?train_loader:
????preds?=?model(x)
????print("Prediction?is?:n",preds)
????print("nActual?targets?is?:n",y)
????break
輸出:
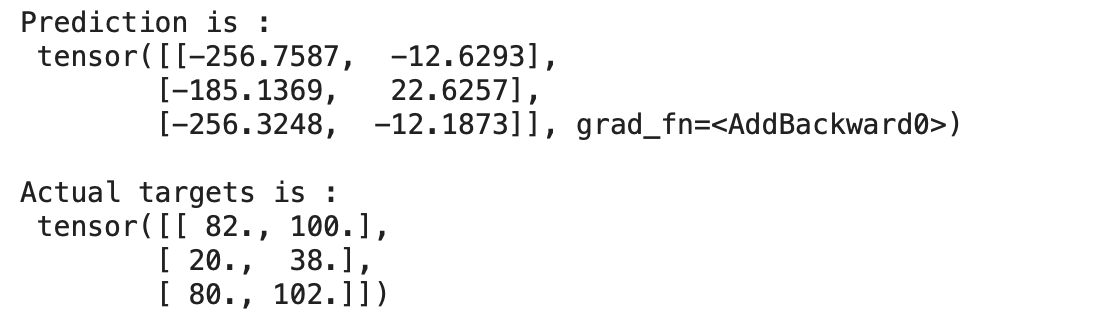
我們可以在上面看到我們的模型預(yù)測的值與實際目標(biāo)相差很大,因為我們的模型是用隨機權(quán)重和偏差初始化的。
顯然,我們不能指望我們隨機初始化的模型表現(xiàn)良好。
損失函數(shù)
損失函數(shù)是衡量模型表現(xiàn)如何的指標(biāo)。損失函數(shù)在更新超參數(shù)方面起著重要作用,因此產(chǎn)生的損失會更少。
回歸最廣泛使用的損失函數(shù)之一是均方誤差或L2 損失。
MSE 定義了實際值和預(yù)測值之間差異的平方平均值。MSE如下:
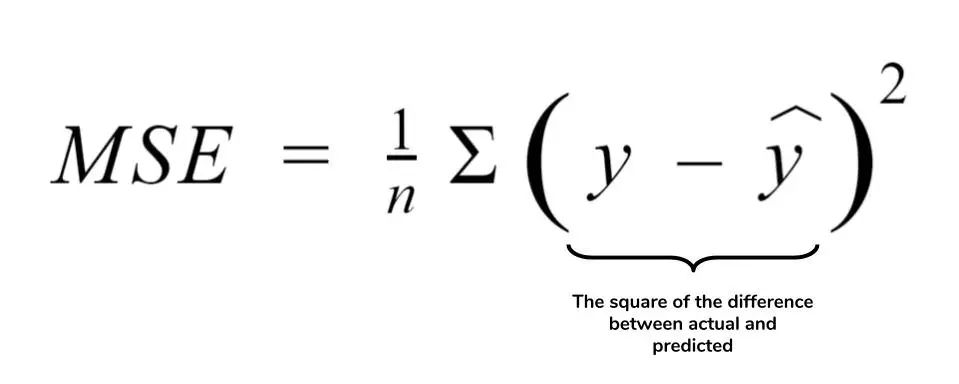
def?mse_loss(predictions,?targets):
????difference?=?predictions?-?targets
????return?torch.sum(difference?*?difference)/?difference.numel()
.numel()方法返回張量中的元素數(shù)。
現(xiàn)在讓我們進行預(yù)測并計算未經(jīng)訓(xùn)練的模型的損失,
for?x,y?in?train_loader:
????preds?=?model(x)
????print("Prediction?is?:n",preds)
????print("nActual?targets?is?:n",y)
????print("nLoss?is:?",mse_loss(preds,?y))
????break
輸出:
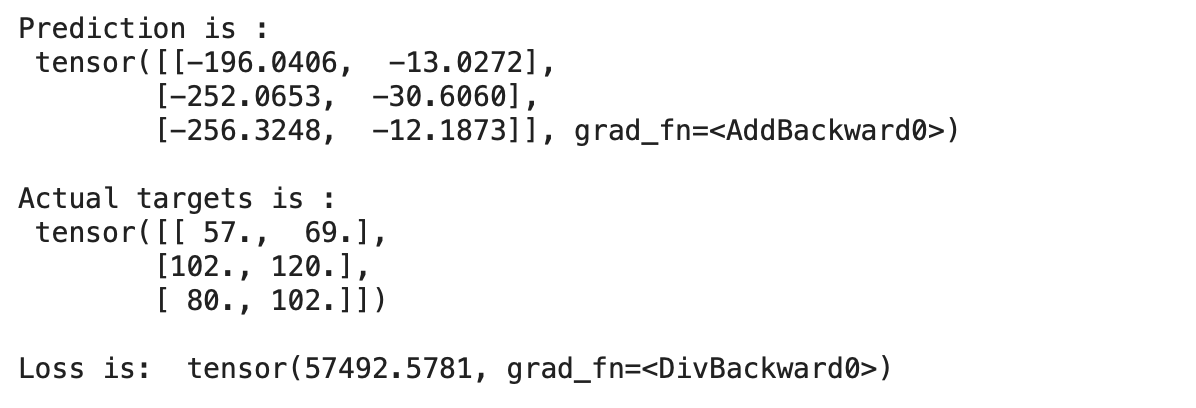
我們可以看到我們的預(yù)測與實際目標(biāo)相差很大,這表明模型的損失很大。
因此,我們應(yīng)該更新權(quán)重和偏差,以減少損失。這可以通過使用稱為梯度下降的優(yōu)化算法來完成。
梯度下降
梯度下降是一種一階迭代優(yōu)化算法,用于尋找可微函數(shù)的局部最小值。這個想法是在當(dāng)前點的函數(shù)梯度(或近似梯度)的相反方向上重復(fù)步驟,因為這是最陡下降的方向。– 維基百科
梯度下降是一種優(yōu)化算法,它計算損失函數(shù)的導(dǎo)數(shù)/梯度以更新權(quán)重并相應(yīng)地減少損失或找到損失函數(shù)的最小值。
在 PyTorch 中實現(xiàn)梯度下降的步驟,
首先,計算損失函數(shù)
求關(guān)于自變量的損失梯度
更新權(quán)重和 bais
重復(fù)以上步驟
現(xiàn)在讓我們開始編碼并實現(xiàn) 50 個 時期的梯度下降,
epochs?=?50
for?i?in?range(epochs):
????#?Iterate?through?training?dataloader
????for?x,y?in?train_loader:
????????#?Generate?Prediction
????????preds?=?model(x)
????????#?Get?the?loss?and?perform?backpropagation
????????loss?=?mse_loss(preds,?y)
????????loss.backward()
????????#?Let's?update?the?weights
????????with?torch.no_grad():
????????????w?-=?w.grad?*1e-6
????????????b?-=?b.grad?*?1e-6
????????????#?Set?the?gradients?to?zero
????????????w.grad.zero_()
????????????b.grad.zero_()
?????print(f"Epoch?{i}/{epochs}:?Loss:?{loss}")
輸出:
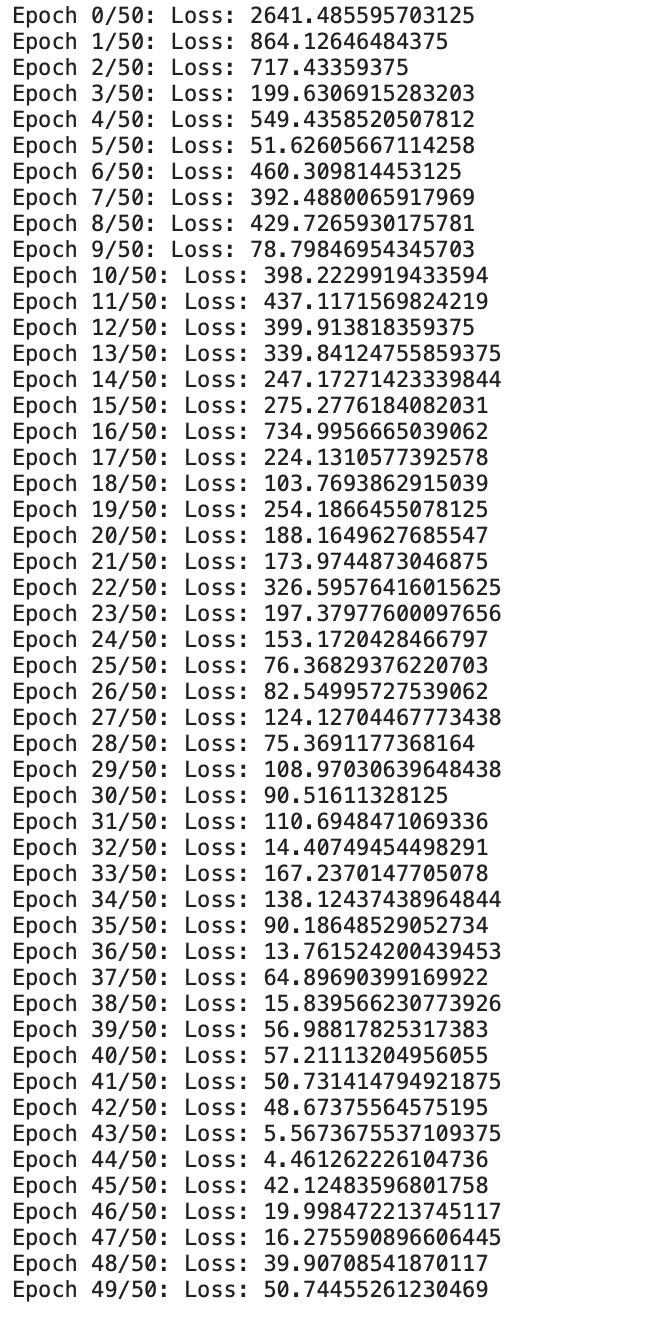
現(xiàn)在我們可以看到我們從頭開始定制的線性回歸模型正在訓(xùn)練給定的數(shù)據(jù)。
我們可以看到損失一直在逐漸減少。現(xiàn)在讓我們檢查一下輸出,
for?x,y?in?train_loader:
????preds?=?model(x)
????print("Prediction?is?:n",preds)
????print("nActual?targets?is?:n",y)
????break
輸出:
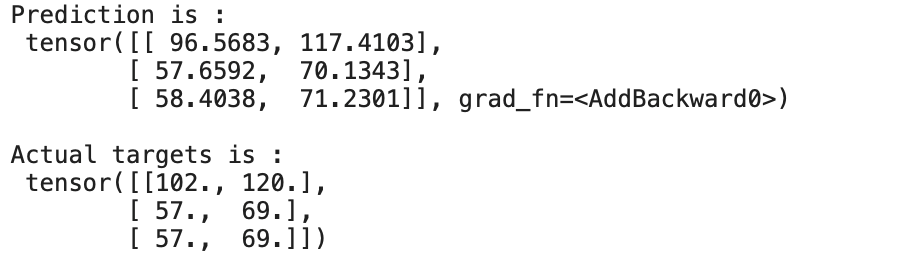
我們可以看到預(yù)測幾乎接近實際目標(biāo)。我們能夠通過訓(xùn)練/更新線性回歸模型的權(quán)重和偏差來預(yù)測 50 個時期。
結(jié)論
這種在數(shù)據(jù)集每次迭代后通過我們基于損失的模型使用梯度下降更新權(quán)重/參數(shù)的過程定義了深度學(xué)習(xí)的基礎(chǔ),它可以解決包括視覺、圖像、文本等在內(nèi)的大量任務(wù)
往期精彩回顧
