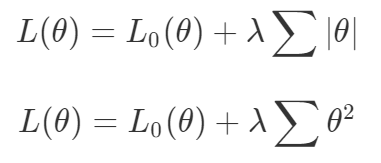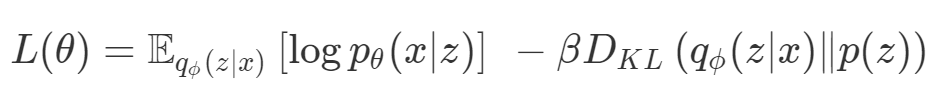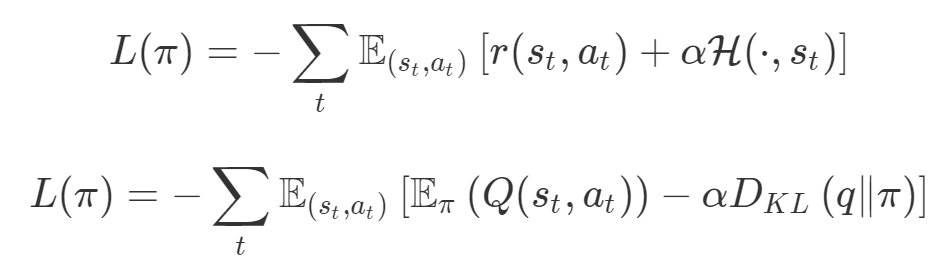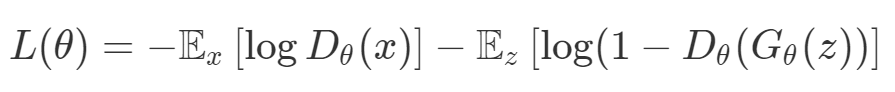在機器學習中,損失的線性組合無處不在。雖然它們帶有一些陷阱,但仍然被廣泛用作標準方法。這些線性組合常常讓算法難以調整。你選擇的損失線性組合是正確的選擇嗎?這篇文章或許能夠給你答案。
機器學習中的許多問題應該被視為多目標問題,但目前并非如此;
「1」中的問題導致這些機器學習算法的超參數(shù)難以調整;
檢測這些問題何時發(fā)生幾乎是不可能的,因此很難解決這些問題。
梯度下降被視為解決所有問題的一種方法。如果一種算法不能解決你的問題,那么就需要花費更多的時間調整超參數(shù)來解決問題。盡管存在單目標的問題,但通常都會對這些目標進行額外的正則化。本文作者從整個機器學習領域選擇了這樣的優(yōu)化目標。首先來說正則化函數(shù)、權重衰減和 Lasso 算法。顯然當你添加了這些正則化,你已經為你的問題創(chuàng)建了多目標損失。畢竟我們關心的是原始損失 L_0 和正則化損失都保持很低。你將會使用λ參數(shù)在這二者之間調整平衡。
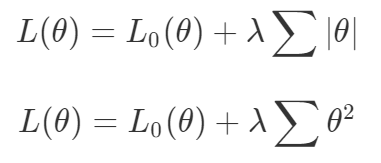
因此,損失(如 VAE 的)實際上是多目標的,第一個目標是最大程度地覆蓋數(shù)據(jù),第二個目標是保持與先前的分布接近。在這種情況下,偶爾會使用 KL 退火來引入一個可調參數(shù)β,以幫助處理這種損失的多目標性。
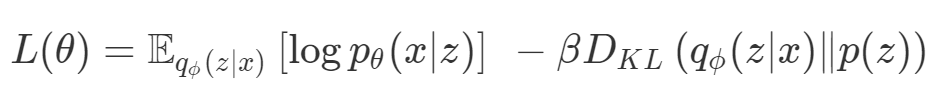
同樣在強化學習中,你也可以發(fā)現(xiàn)這種多目標性。在許多環(huán)境中,簡單地將為達成部分目的而獲得的獎勵加起來很普遍。策略損失也通常是損失的線性組合。以下是 PPO、SAC 和 MPO 的策略損失及其可調整參數(shù)α的熵正則化方法。
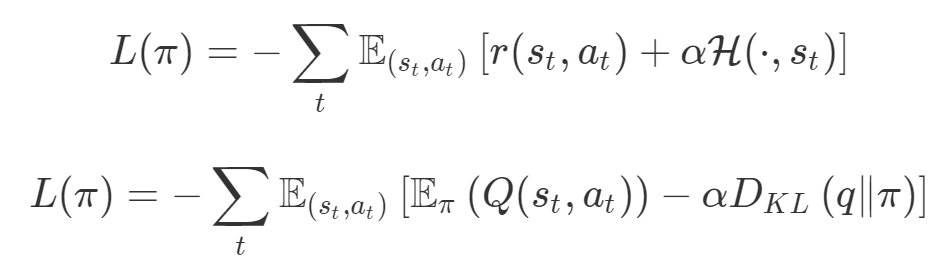
最后,GAN 損失當然是判別器損失和生成器損失的和:
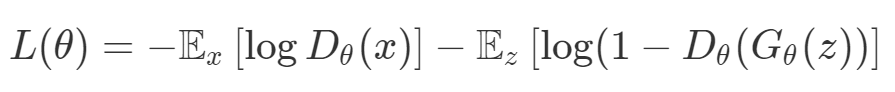
所有這些損失都有一些共性,研究者們正在嘗試同時針對多個目標進行高效優(yōu)化,并且認為最佳情況是在平衡這些通常相互矛盾的力量時找到的。在某些情況下,求和方式更加具體,并且引入了超參數(shù)以判斷各部分的權重。在某些情況下,組合損失的方式有明確的理論基礎,并且不需要使用超參數(shù)來調整各部分之間的平衡。一些組合損失的方法聽起來很有吸引力,但實際上是不穩(wěn)定且危險的。平衡行為通常更像是在「走鋼絲」。考慮一個簡單的情況,我們嘗試對損失的線性組合進行優(yōu)化。我們采用優(yōu)化總損失(損失的總和)的方法,使用梯度下降來對此進行優(yōu)化,觀察到以下行為:
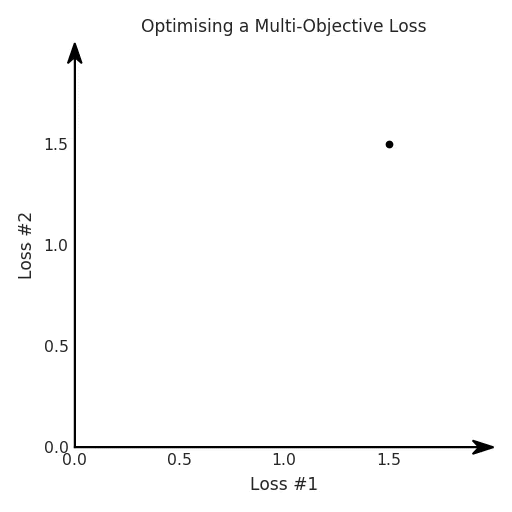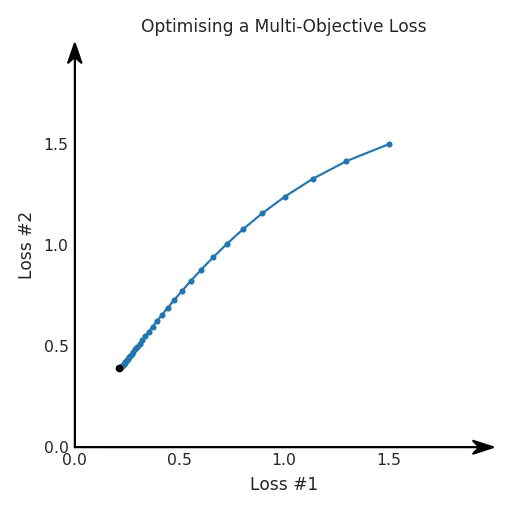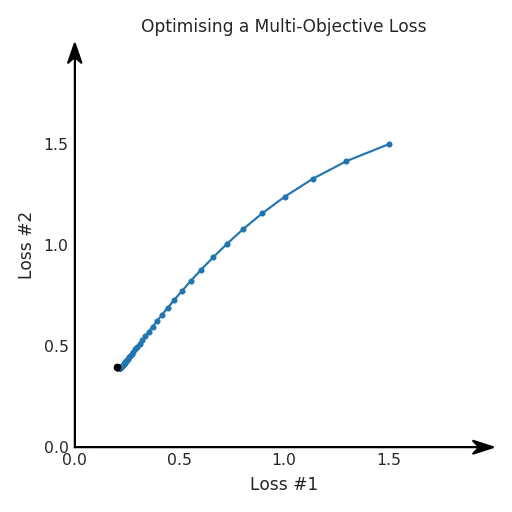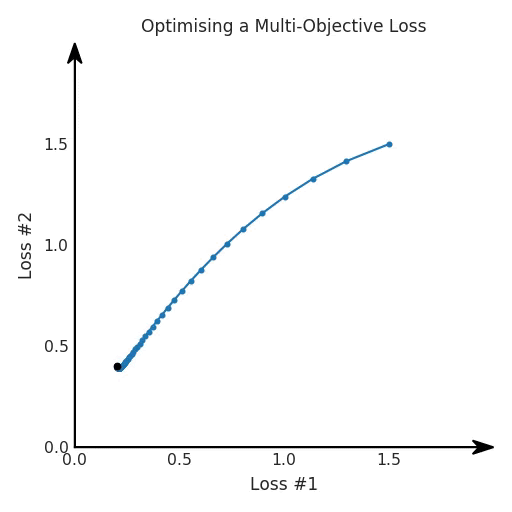
def loss(θ):return loss_1(θ) + loss_2(θ)loss_derivative = grad(loss)for gradient_step in range(200): gradient = loss_derivative(θ) θ = θ - 0.02 * gradient
通常情況下,我們對兩個損失之間的權衡并不滿意,因此在第二個損失上引入了比例系數(shù)α,并運行了以下代碼:def loss(θ, α):return loss_1(θ) + α*loss_2(θ)loss_derivative = grad(loss)for gradient_step in range(200): gradient = loss_derivative(θ, α=0.5) θ = θ - 0.02 * gradient
我們希望看到:當調整 α 時,可以選擇兩個損失之間的折衷,并選擇最適合自身應用的點。我們將有效地進行一個超參數(shù)調整回路,手動選擇一個α來運行優(yōu)化過程,決定降低第二個損失,并相應地調整α并重復整個優(yōu)化過程。經過幾次迭代,我們滿足于找到的解,并繼續(xù)寫論文。但是,事實并非總是如此。有時,問題的實際行為如下動圖所示:
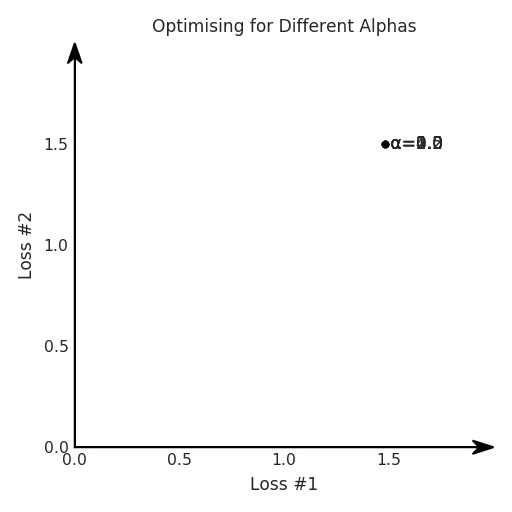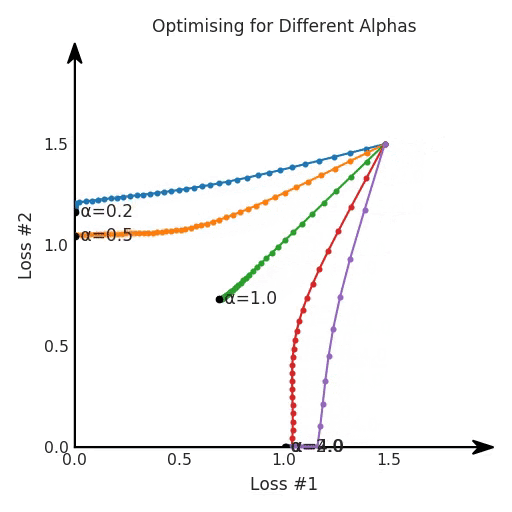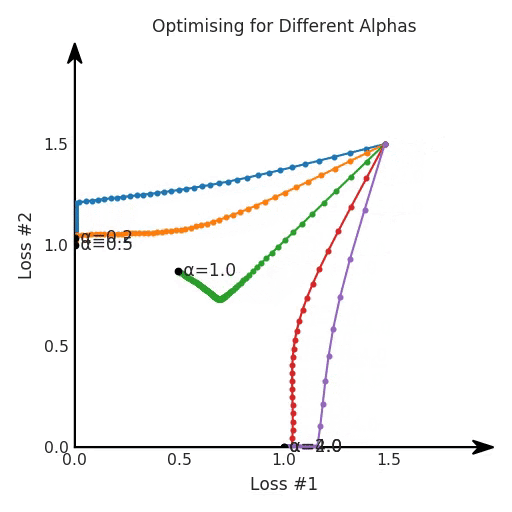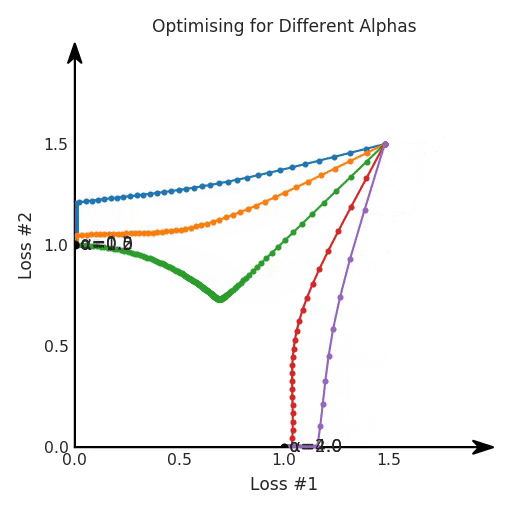
看起來無論怎樣調整參數(shù)α,都不能很好地權衡兩種損失。
我們看到了兩類解決方案,它們都分別忽略了一種損失。但是,這兩種解決方案都不適用于大多數(shù)應用。在大多數(shù)情況下,兩種損失更加平衡的點是可取的解決方案。實際上,這種關于訓練過程中兩種損失的圖表幾乎從未繪制過,因此該圖中所示的動態(tài)情況常常無法觀察到。我們只觀察繪制總體損失的訓練曲線,并且得出超參數(shù)需要更多時間調整的結論。也許我們可以采取一種早停法(early stopping),以使得論文中的數(shù)據(jù)是有效的。畢竟,審稿人喜歡高效的數(shù)據(jù)。問題出在哪里呢?為什么這種方法有時有效,有時卻無法提供可調參數(shù)?為此,我們需要更深入地研究一下以下兩個動圖之間的差異。它們都是針對相同的問題,使用相同的損失函數(shù)生成的,并且正在使用相同的優(yōu)化方法來優(yōu)化這些損失。因此,這些都不是造成差異的原因。在這些問題之間發(fā)生變化的是模型。換句話說,模型參數(shù)θ對模型輸出的影響是不同的。因此,讓我們可視化一下通常不可見的東西,這是兩個優(yōu)化的帕累托前沿。這是模型可以實現(xiàn)且是不受其他任何解決方案支配的解決方案的集合。換句話說,這是一組可實現(xiàn)的損失,沒有一個點可以使所有損失都變得更好。無論你如何選擇在兩個損失之間進行權衡,首選的解決方案始終依賴帕累托前沿。通常,通過調整損失的超參數(shù),你通常希望僅在同一個前沿找到一個不同的點。
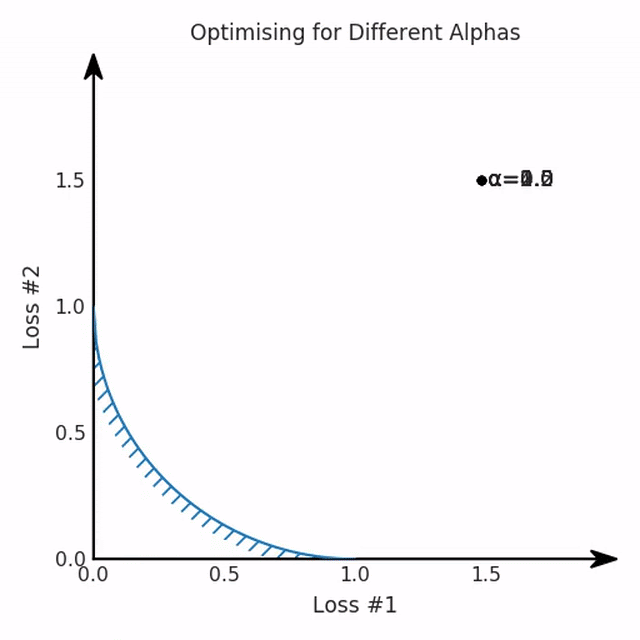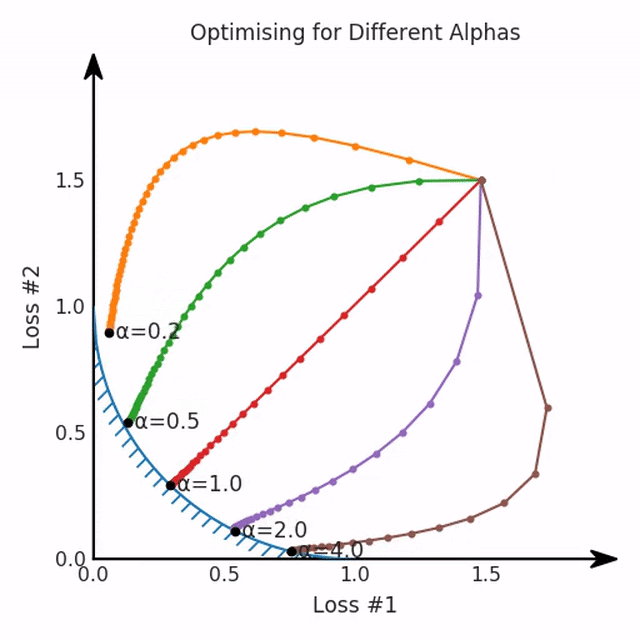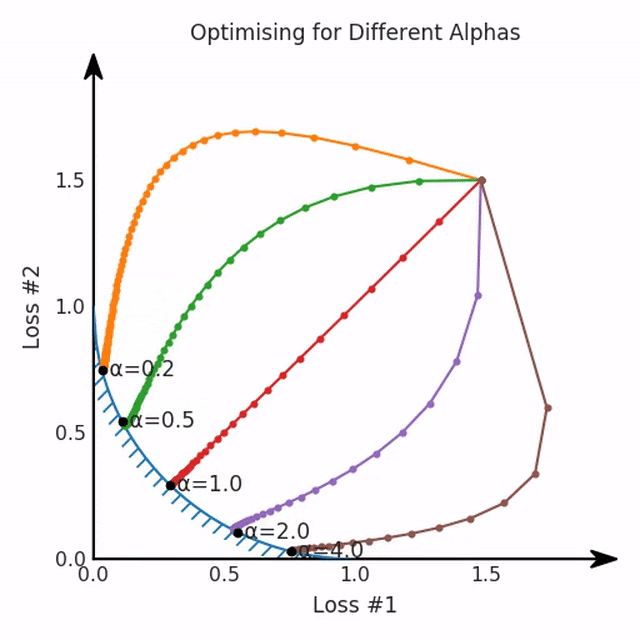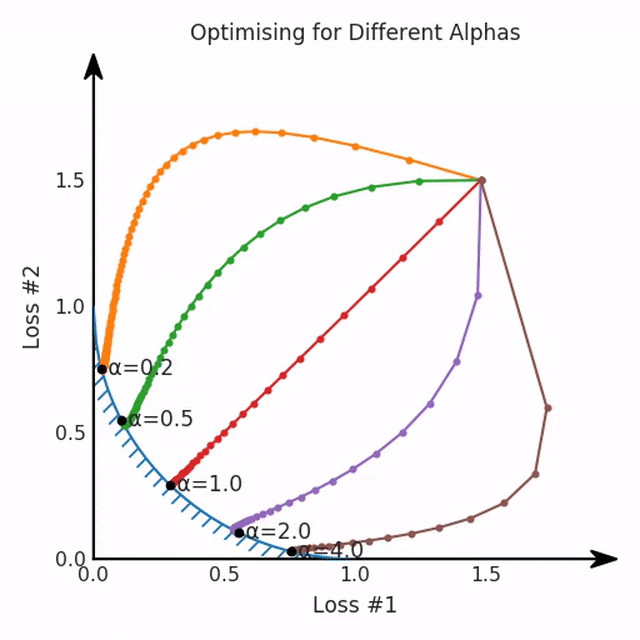
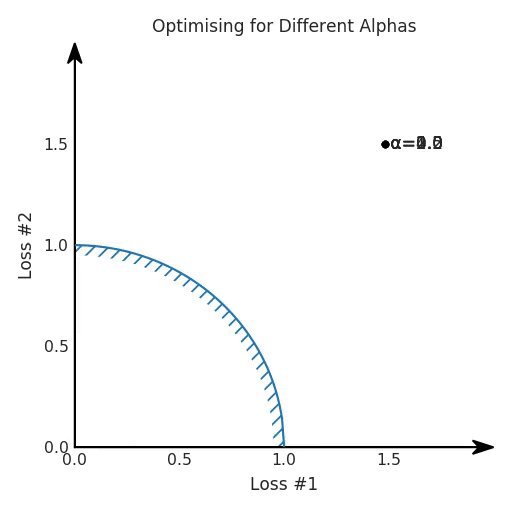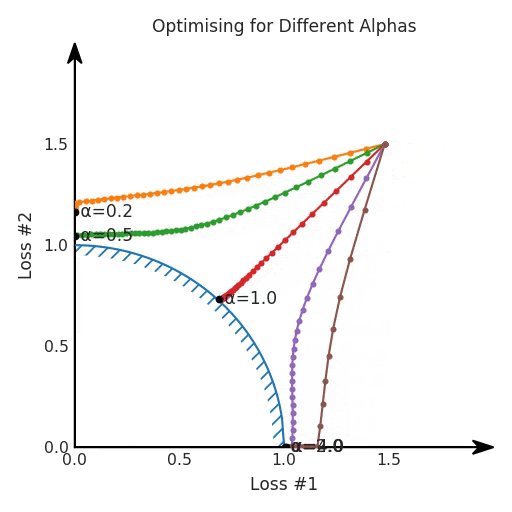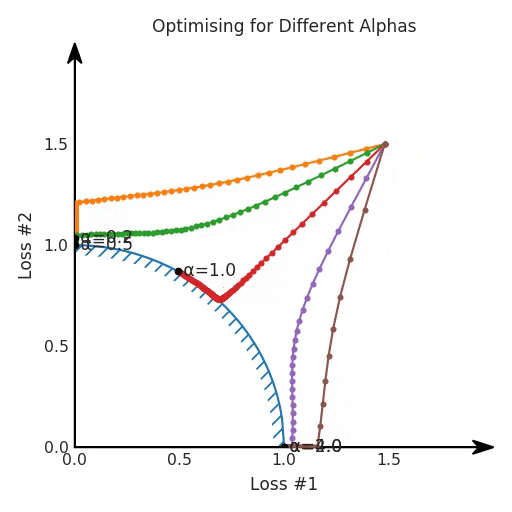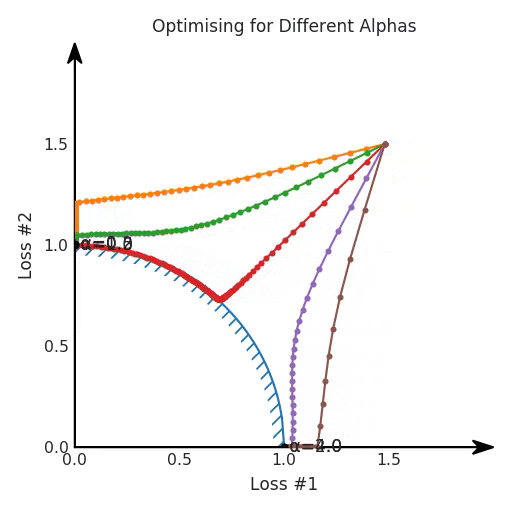
兩個帕累托前沿之間的差異會使得第一種情況的調優(yōu)效果很好,但是在更改模型后卻嚴重失敗了。事實證明,當帕累托前沿為凸形時,我們可以通過調整α參數(shù)來實現(xiàn)所有可能的權衡效果。但是,當帕累托前沿為凹形時,該方法似乎不再有效。
為什么凹帕累托前沿面的梯度下降優(yōu)化會失敗?
通過查看第三個維度中的總體損失,可以發(fā)現(xiàn)實際上是用梯度下降優(yōu)化了損失。在下圖中,我們可視化了相對于每個損失的總損失平面。實際上是使用參數(shù)的梯度下降到該平面上,采取的每個梯度下降步驟也必將在該平面上向下移動。你可以想象成梯度下降優(yōu)化過程是在該平面上放置一個球形小卵石,使其在重力作用下向下移動直到它停下來。優(yōu)化過程停止的點是優(yōu)化過程的結果,此處用星星表示。如下圖所示,無論你如何上下擺動該平面,最終都將得到最佳結果。
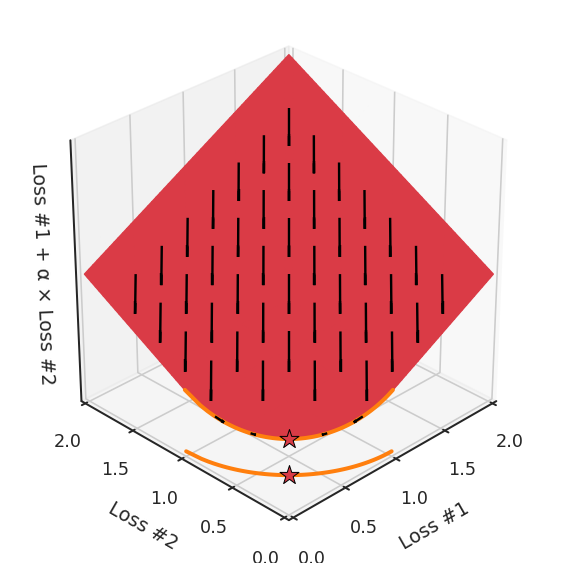
通過調整α,此空間將保持一個平面。畢竟更改α只會更改該平面的傾斜度。在凸的情況下,可以通過調整α來實現(xiàn)帕累托曲線上的任何解。α大一點會將星星拉到左側,α小一點會將星星拉到右側。優(yōu)化過程的每個起點都將在相同的解上收斂,這對于α的所有值都是正確的。
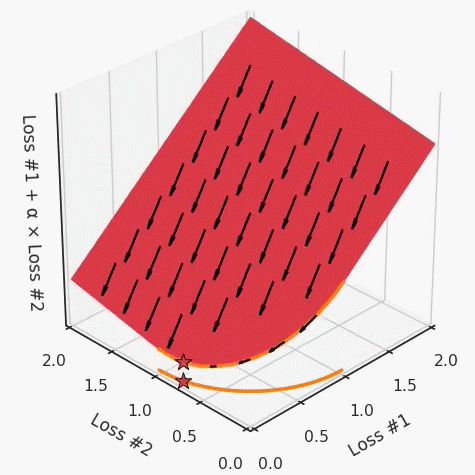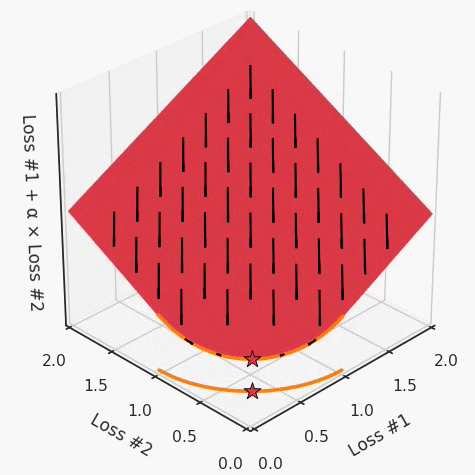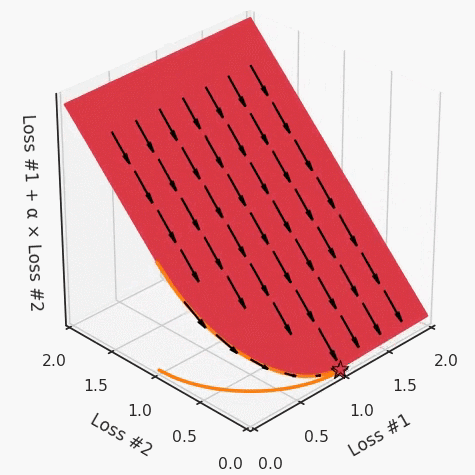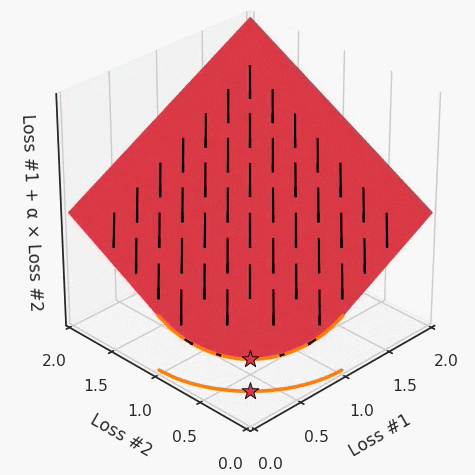
但是,如果我們看一下具有凹帕累托前沿面的不同模型問題,那么問題出現(xiàn)在哪里就變得顯而易見了。
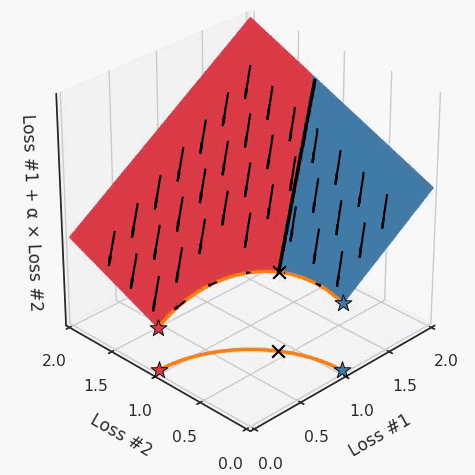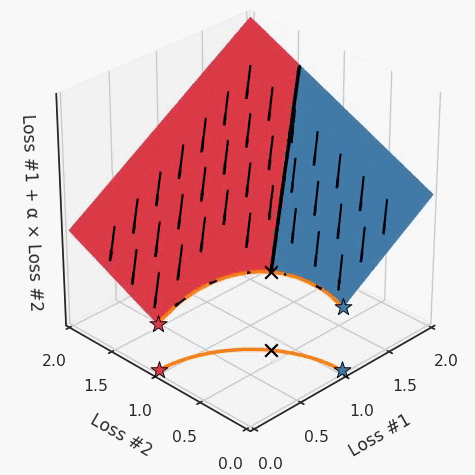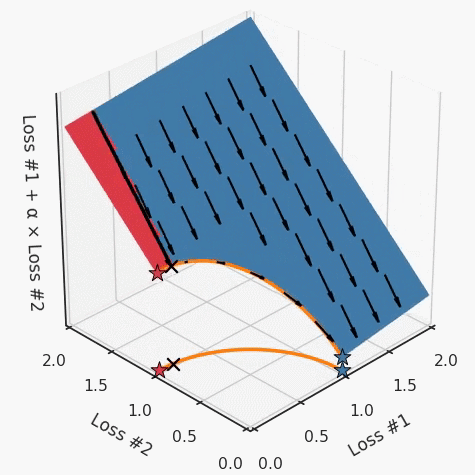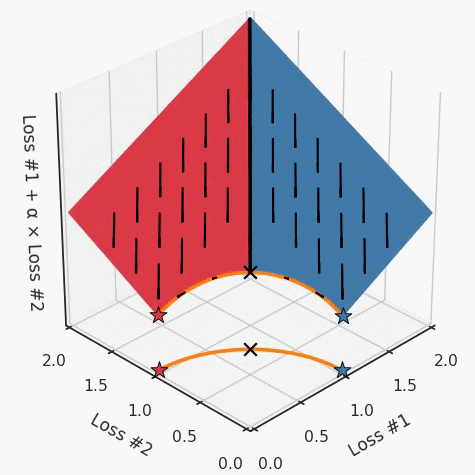
如果我們想象卵石遵循該平面上的梯度:有時向左滾動更多,有時向右滾動更多,但始終向下滾動。然后很明顯它最終將到達兩個角點之一,即紅色星或藍色星。當我們調整α時,該平面以與凸情況下完全相同的方式傾斜,但由于帕累托前沿面的形狀,將永遠只能到達該前沿面上的兩個點,即凹曲線末端的兩個點。使用基于梯度下降方法無法找到曲線上的 × 點(實際上想要達到的點)。為什么?因為這是一個鞍點(saddle point)。同樣要注意的是,當我們調整α時會發(fā)生什么。我們可以觀察到,相對于其他解,一個解需要調整多少個起點,但我們無法調整以找到帕累托前沿面上的其他解。
第一,即使沒有引入超參數(shù)來權衡損失,說梯度下降試圖在反作用力之間保持平衡也是不正確的。根據(jù)模型可實現(xiàn)的解,可以完全忽略其中一種損失,而將注意力放在另一種損失上,反之亦然,這取決于初始化模型的位置;
第二,即使引入了超參數(shù),也將在嘗試后的基礎上調整此超參數(shù)。研究中往往是運行一個完整的優(yōu)化過程,然后確定是否滿意,再對超參數(shù)進行微調。重復此優(yōu)化循環(huán),直到對性能滿意為止。這是一種費時費力的方法,通常涉及多次運行梯度下降的迭代;
第三,超參數(shù)不能針對所有的最優(yōu)情況進行調整。無論進行多少調整和微調,你都不會找到可能感興趣的中間方案。這不是因為它們不存在,它們一定存在,只是因為選擇了一種糟糕的組合損失方法;
第四,必須強調的是,對于實際應用,帕累托前沿面是否為凸面以及因此這些損失權重是否可調始終是未知的。它們是否是好的超參數(shù),取決于模型的參數(shù)化方式及其影響帕累托曲線的方式。但是,對于任何實際應用,都無法可視化或分析帕累托曲線。可視化比原始的優(yōu)化問題要困難得多。因此出現(xiàn)問題并不會引起注意;
最后,如果你真的想使用這些線性權重來進行權衡,則需要明確證明整個帕累托曲線對于正在使用的特定模型是凸的。因此,使用相對于模型輸出而言凸的損失不足以避免問題。如果參數(shù)化空間很大(如果優(yōu)化涉及神經網絡內部的權重,則情況總是如此),你可能會忘記嘗試這種證明。需要強調的是,基于某些中間潛勢(intermediate latent),顯示這些損失的帕累托曲線的凸度不足以表明你具有可調參數(shù)。凸度實際上需要取決于參數(shù)空間以及可實現(xiàn)解決方案的帕累托前沿面。
請注意,在大多數(shù)應用中,帕累托前沿面既不是凸的也不是凹的,而是二者的混合體,這擴大了問題。
以一個帕累托前沿面為例,凸塊之間有凹塊。每個凹塊不僅可以確保無法通過梯度下降找到解,還可以將參數(shù)初始化的空間分成兩部分,一部分可以在一側的凸塊上找到解,而另一部分智能在另一側上找到解。如下動圖所示,在帕累托前沿面上有多個凹塊會使問題更加復雜。
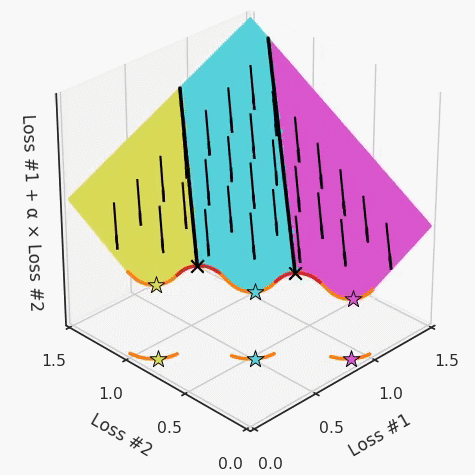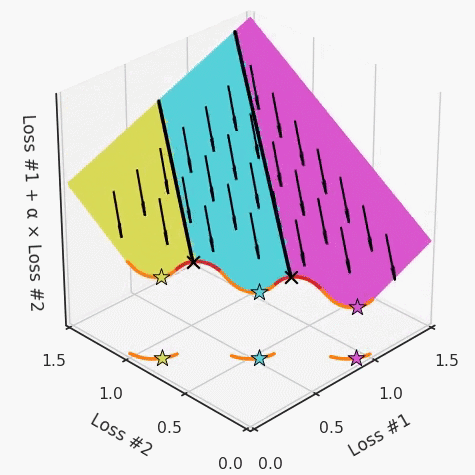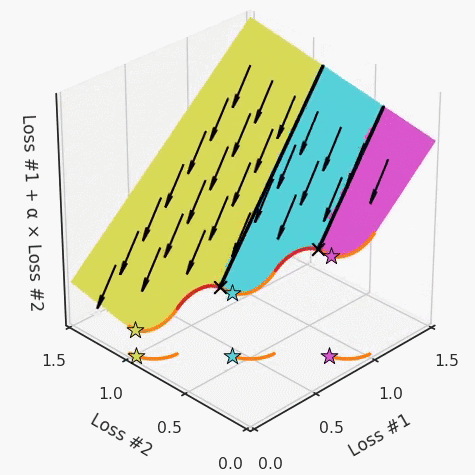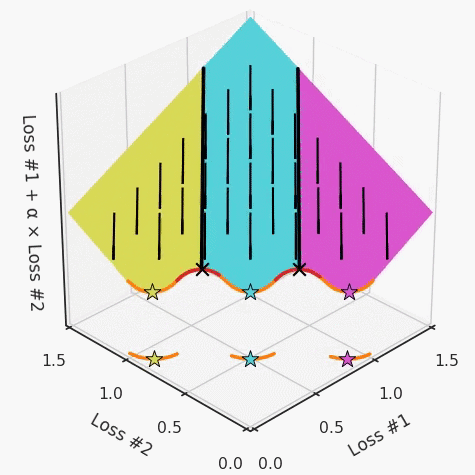
因此,我們不僅具有無法找到所有解的超參數(shù)α,而且根據(jù)初始化,它可能會找到帕累托曲線的不同凸部分。此參數(shù)和初始化以令人困惑的方式相互混合,這讓問題更加困難。如果稍微調整參數(shù)以希望稍微移動最優(yōu)值,則即使保持相同的初始化,也可能會突然跳到帕累托前沿面的其他凸部分。原文鏈接:https://engraved.ghost.io/why-machine-learning-algorithms-are-hard-to-tune/?------------------------------------------------
雙一流高校研究生團隊創(chuàng)建 ↓
專注于目標檢測原創(chuàng)并分享相關知識 ?
整理不易,點贊三連!