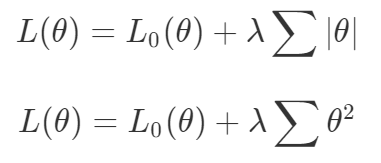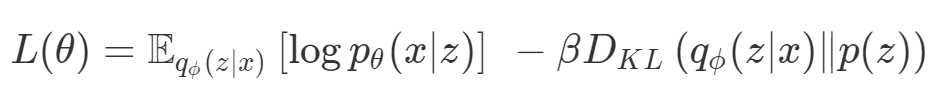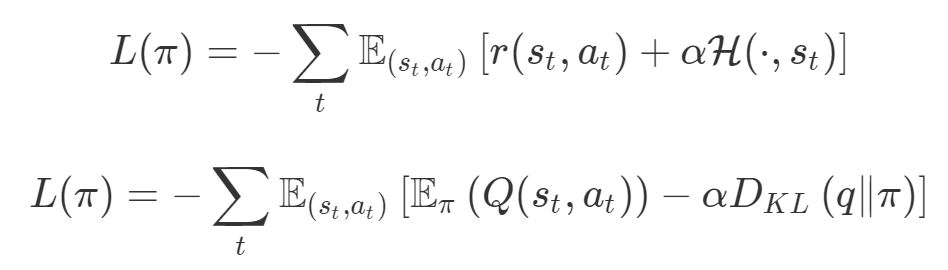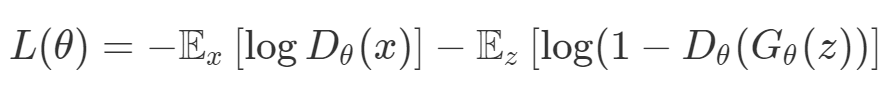本文約3500字,建議閱讀9分鐘
本文介紹了一些關(guān)于機(jī)器學(xué)習(xí)和線性組合的部分問題以及緩解該問題的方法。
在機(jī)器學(xué)習(xí)中,損失的線性組合無處不在。雖然它們帶有一些陷阱,但仍然被廣泛用作標(biāo)準(zhǔn)方法。這些線性組合常常讓算法難以調(diào)整。- 機(jī)器學(xué)習(xí)中的許多問題應(yīng)該被視為多目標(biāo)問題,但目前并非如此;
- 「1」中的問題導(dǎo)致這些機(jī)器學(xué)習(xí)算法的超參數(shù)難以調(diào)整;
- 檢測(cè)這些問題何時(shí)發(fā)生幾乎是不可能的,因此很難解決這些問題。
梯度下降被視為解決所有問題的一種方法。如果一種算法不能解決你的問題,那么就需要花費(fèi)更多的時(shí)間調(diào)整超參數(shù)來解決問題。盡管存在單目標(biāo)的問題,但通常都會(huì)對(duì)這些目標(biāo)進(jìn)行額外的正則化。本文作者從整個(gè)機(jī)器學(xué)習(xí)領(lǐng)域選擇了這樣的優(yōu)化目標(biāo)。首先來說正則化函數(shù)、權(quán)重衰減和 Lasso 算法。顯然當(dāng)你添加了這些正則化,你已經(jīng)為你的問題創(chuàng)建了多目標(biāo)損失。畢竟我們關(guān)心的是原始損失 L_0 和正則化損失都保持很低。你將會(huì)使用λ參數(shù)在這二者之間調(diào)整平衡。因此,損失(如 VAE 的)實(shí)際上是多目標(biāo)的,第一個(gè)目標(biāo)是最大程度地覆蓋數(shù)據(jù),第二個(gè)目標(biāo)是保持與先前的分布接近。在這種情況下,偶爾會(huì)使用 KL 退火來引入一個(gè)可調(diào)參數(shù)β,以幫助處理這種損失的多目標(biāo)性。同樣在強(qiáng)化學(xué)習(xí)中,你也可以發(fā)現(xiàn)這種多目標(biāo)性。在許多環(huán)境中,簡(jiǎn)單地將為達(dá)成部分目的而獲得的獎(jiǎng)勵(lì)加起來很普遍。策略損失也通常是損失的線性組合。以下是 PPO、SAC 和 MPO 的策略損失及其可調(diào)整參數(shù)α的熵正則化方法。最后,GAN 損失當(dāng)然是判別器損失和生成器損失的和:所有這些損失都有一些共性,研究者們正在嘗試同時(shí)針對(duì)多個(gè)目標(biāo)進(jìn)行高效優(yōu)化,并且認(rèn)為最佳情況是在平衡這些通常相互矛盾的力量時(shí)找到的。在某些情況下,求和方式更加具體,并且引入了超參數(shù)以判斷各部分的權(quán)重。在某些情況下,組合損失的方式有明確的理論基礎(chǔ),并且不需要使用超參數(shù)來調(diào)整各部分之間的平衡。一些組合損失的方法聽起來很有吸引力,但實(shí)際上是不穩(wěn)定且危險(xiǎn)的。平衡行為通常更像是在「走鋼絲」。考慮一個(gè)簡(jiǎn)單的情況,我們嘗試對(duì)損失的線性組合進(jìn)行優(yōu)化。我們采用優(yōu)化總損失(損失的總和)的方法,使用梯度下降來對(duì)此進(jìn)行優(yōu)化,觀察到以下行為:def loss(θ):return loss_1(θ) + loss_2(θ)loss_derivative = grad(loss)for gradient_step in range(200): gradient = loss_derivative(θ) θ = θ - 0.02 * gradient
通常情況下,我們對(duì)兩個(gè)損失之間的權(quán)衡并不滿意,因此在第二個(gè)損失上引入了比例系數(shù)α,并運(yùn)行了以下代碼:def loss(θ, α):return loss_1(θ) + α*loss_2(θ)loss_derivative = grad(loss)for gradient_step in range(200): gradient = loss_derivative(θ, α=0.5) θ = θ - 0.02 * gradient
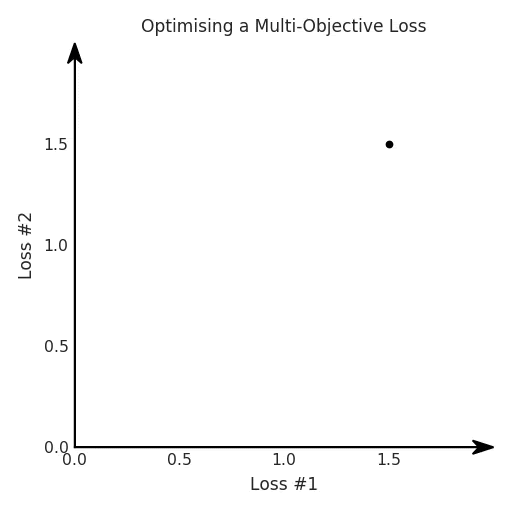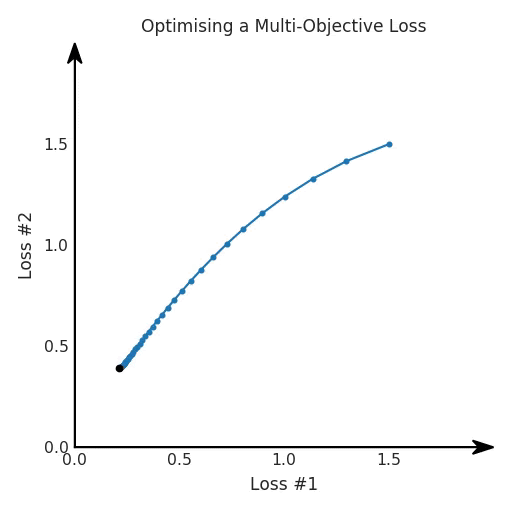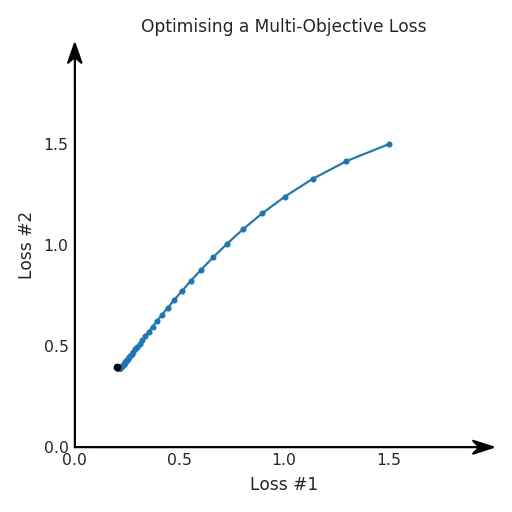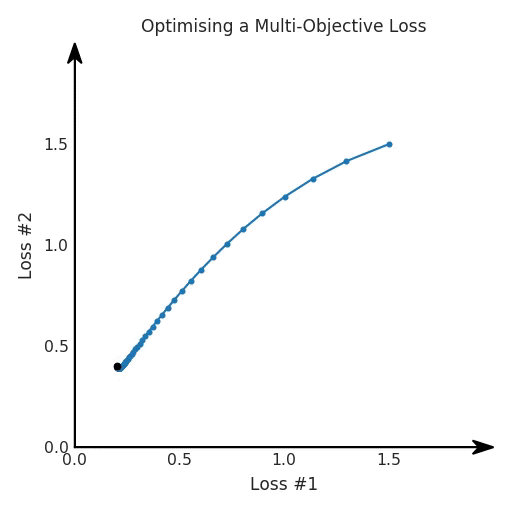
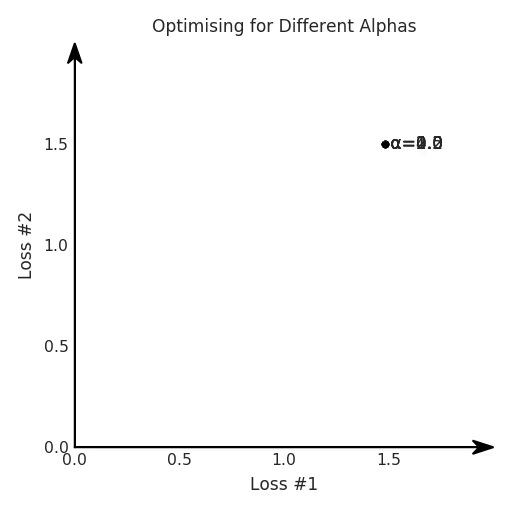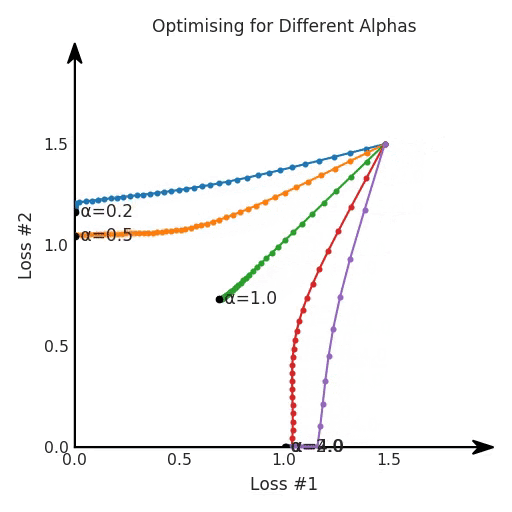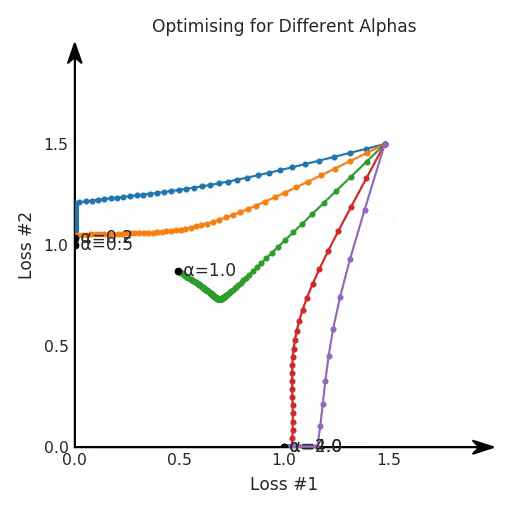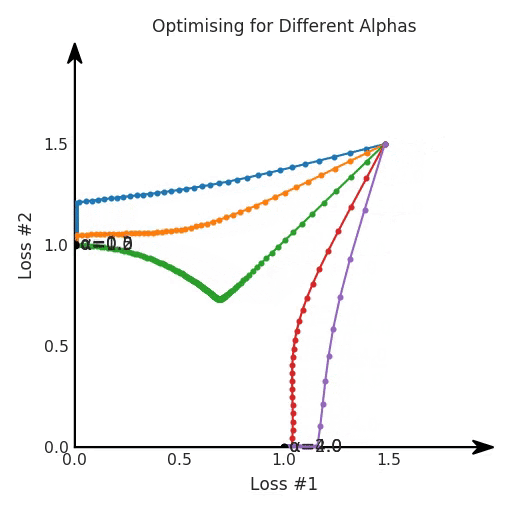
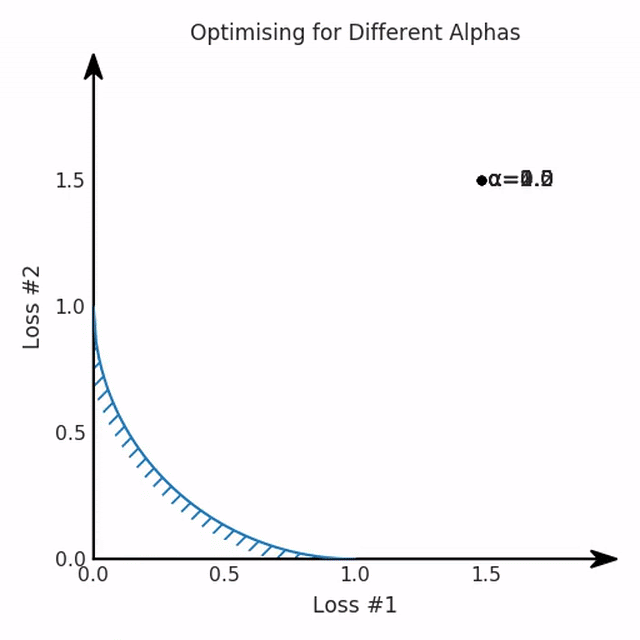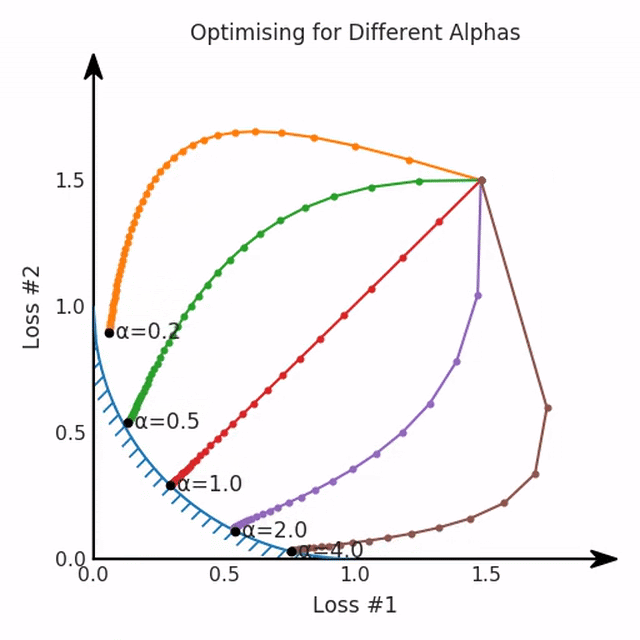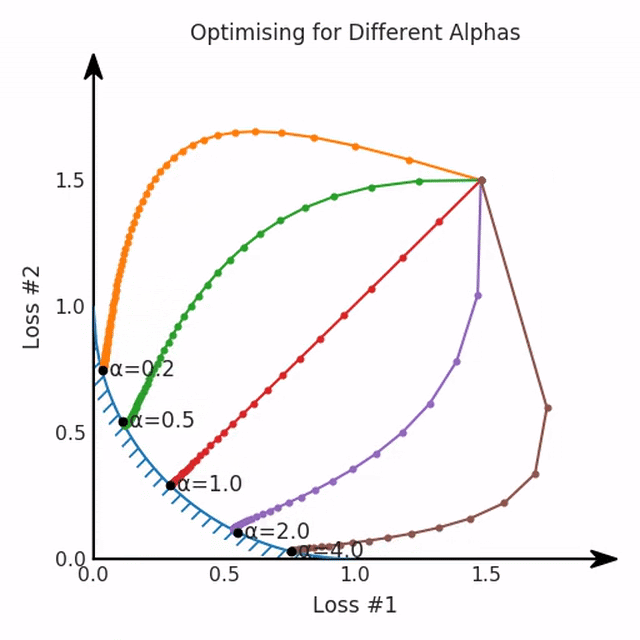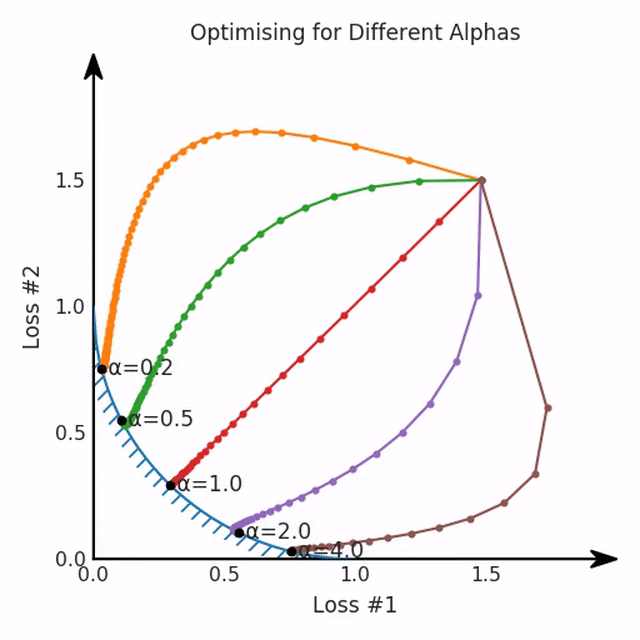
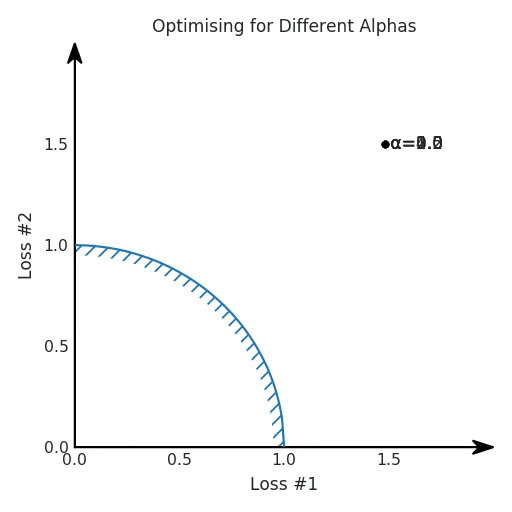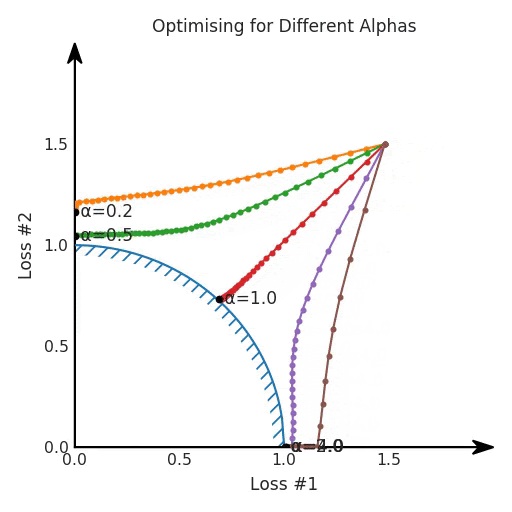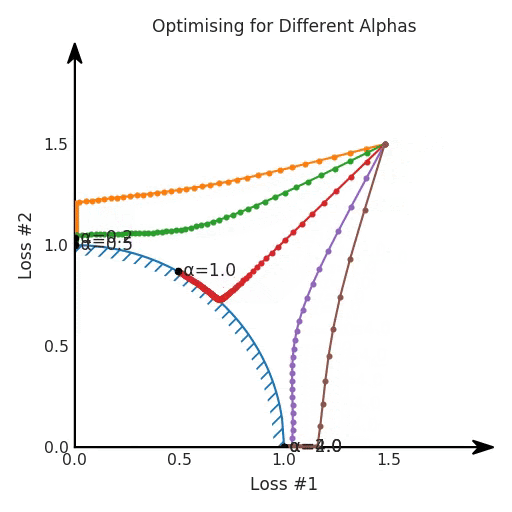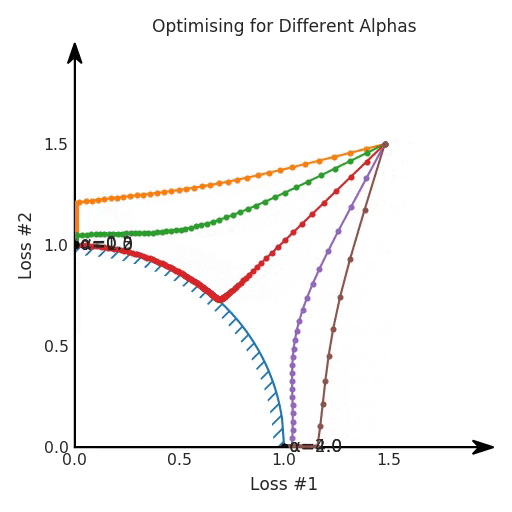
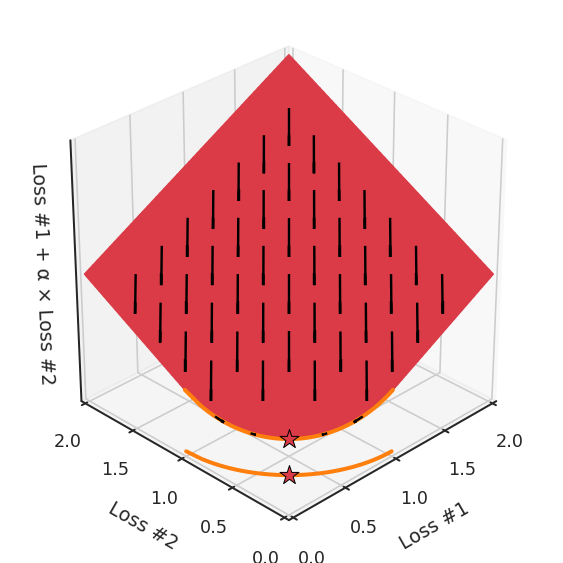
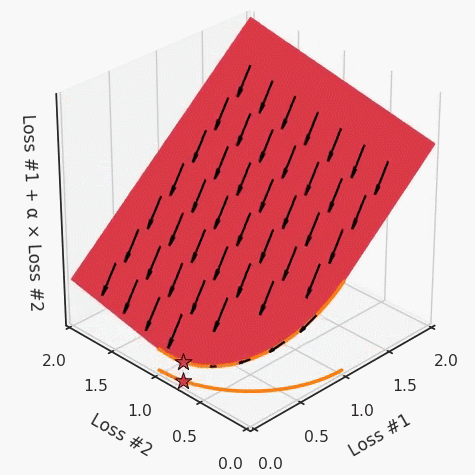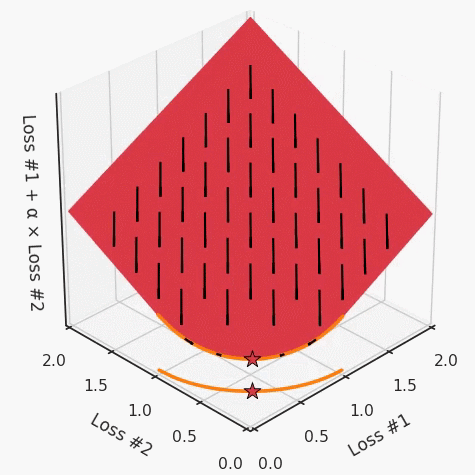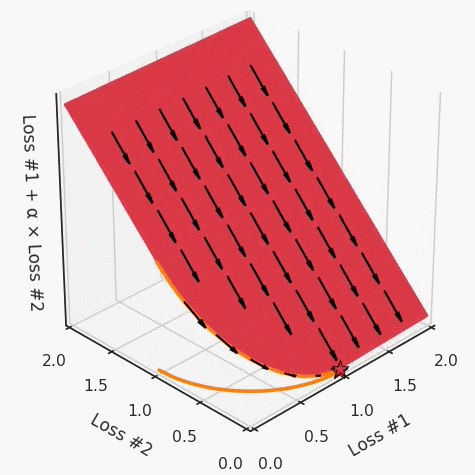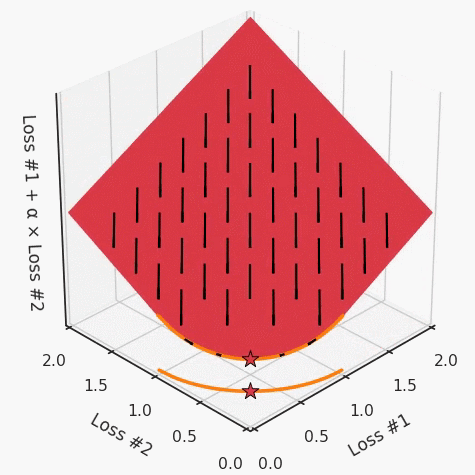
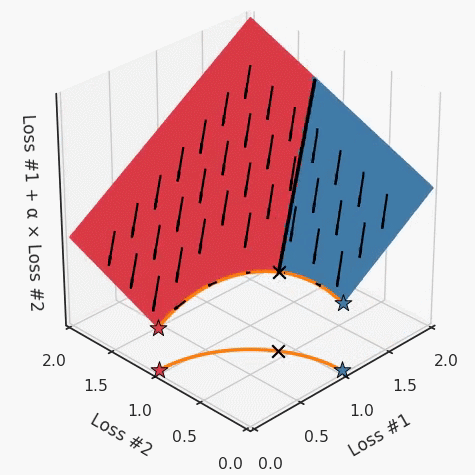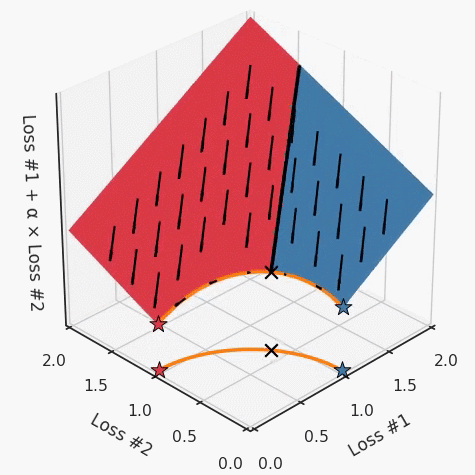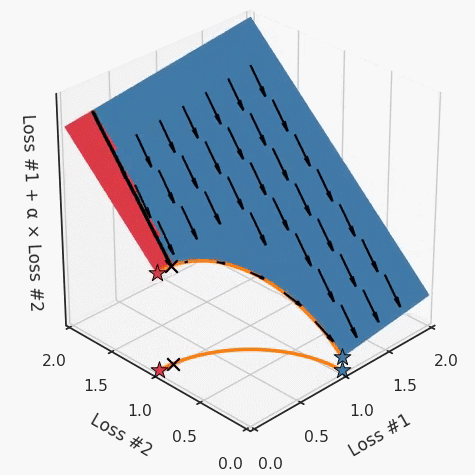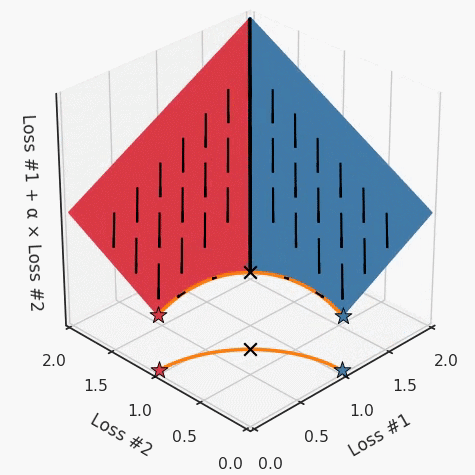
我們希望看到:當(dāng)調(diào)整 α 時(shí),可以選擇兩個(gè)損失之間的折衷,并選擇最適合自身應(yīng)用的點(diǎn)。我們將有效地進(jìn)行一個(gè)超參數(shù)調(diào)整回路,手動(dòng)選擇一個(gè)α來運(yùn)行優(yōu)化過程,決定降低第二個(gè)損失,并相應(yīng)地調(diào)整α并重復(fù)整個(gè)優(yōu)化過程。經(jīng)過幾次迭代,我們滿足于找到的解,并繼續(xù)寫論文。但是,事實(shí)并非總是如此。有時(shí),問題的實(shí)際行為如下動(dòng)圖所示:看起來無論怎樣調(diào)整參數(shù)α,都不能很好地權(quán)衡兩種損失。我們看到了兩類解決方案,它們都分別忽略了一種損失。但是,這兩種解決方案都不適用于大多數(shù)應(yīng)用。在大多數(shù)情況下,兩種損失更加平衡的點(diǎn)是可取的解決方案。實(shí)際上,這種關(guān)于訓(xùn)練過程中兩種損失的圖表幾乎從未繪制過,因此該圖中所示的動(dòng)態(tài)情況常常無法觀察到。我們只觀察繪制總體損失的訓(xùn)練曲線,并且得出超參數(shù)需要更多時(shí)間調(diào)整的結(jié)論。也許我們可以采取一種早停法(early stopping),以使得論文中的數(shù)據(jù)是有效的。畢竟,審稿人喜歡高效的數(shù)據(jù)。問題出在哪里呢?為什么這種方法有時(shí)有效,有時(shí)卻無法提供可調(diào)參數(shù)?為此,我們需要更深入地研究一下以下兩個(gè)動(dòng)圖之間的差異。它們都是針對(duì)相同的問題,使用相同的損失函數(shù)生成的,并且正在使用相同的優(yōu)化方法來優(yōu)化這些損失。因此,這些都不是造成差異的原因。在這些問題之間發(fā)生變化的是模型。換句話說,模型參數(shù)θ對(duì)模型輸出的影響是不同的。因此,讓我們可視化一下通常不可見的東西,這是兩個(gè)優(yōu)化的帕累托前沿。這是模型可以實(shí)現(xiàn)且是不受其他任何解決方案支配的解決方案的集合。換句話說,這是一組可實(shí)現(xiàn)的損失,沒有一個(gè)點(diǎn)可以使所有損失都變得更好。無論你如何選擇在兩個(gè)損失之間進(jìn)行權(quán)衡,首選的解決方案始終依賴帕累托前沿。通常,通過調(diào)整損失的超參數(shù),你通常希望僅在同一個(gè)前沿找到一個(gè)不同的點(diǎn)。兩個(gè)帕累托前沿之間的差異會(huì)使得第一種情況的調(diào)優(yōu)效果很好,但是在更改模型后卻嚴(yán)重失敗了。事實(shí)證明,當(dāng)帕累托前沿為凸形時(shí),我們可以通過調(diào)整α參數(shù)來實(shí)現(xiàn)所有可能的權(quán)衡效果。但是,當(dāng)帕累托前沿為凹形時(shí),該方法似乎不再有效。為什么凹帕累托前沿面的梯度下降優(yōu)化會(huì)失敗?通過查看第三個(gè)維度中的總體損失,可以發(fā)現(xiàn)實(shí)際上是用梯度下降優(yōu)化了損失。在下圖中,我們可視化了相對(duì)于每個(gè)損失的總損失平面。實(shí)際上是使用參數(shù)的梯度下降到該平面上,采取的每個(gè)梯度下降步驟也必將在該平面上向下移動(dòng)。你可以想象成梯度下降優(yōu)化過程是在該平面上放置一個(gè)球形小卵石,使其在重力作用下向下移動(dòng)直到它停下來。優(yōu)化過程停止的點(diǎn)是優(yōu)化過程的結(jié)果,此處用星星表示。如下圖所示,無論你如何上下擺動(dòng)該平面,最終都將得到最佳結(jié)果。通過調(diào)整α,此空間將保持一個(gè)平面。畢竟更改α只會(huì)更改該平面的傾斜度。在凸的情況下,可以通過調(diào)整α來實(shí)現(xiàn)帕累托曲線上的任何解。α大一點(diǎn)會(huì)將星星拉到左側(cè),α小一點(diǎn)會(huì)將星星拉到右側(cè)。優(yōu)化過程的每個(gè)起點(diǎn)都將在相同的解上收斂,這對(duì)于α的所有值都是正確的。但是,如果我們看一下具有凹帕累托前沿面的不同模型問題,那么問題出現(xiàn)在哪里就變得顯而易見了。如果我們想象卵石遵循該平面上的梯度:有時(shí)向左滾動(dòng)更多,有時(shí)向右滾動(dòng)更多,但始終向下滾動(dòng)。然后很明顯它最終將到達(dá)兩個(gè)角點(diǎn)之一,即紅色星或藍(lán)色星。當(dāng)我們調(diào)整α?xí)r,該平面以與凸情況下完全相同的方式傾斜,但由于帕累托前沿面的形狀,將永遠(yuǎn)只能到達(dá)該前沿面上的兩個(gè)點(diǎn),即凹曲線末端的兩個(gè)點(diǎn)。使用基于梯度下降方法無法找到曲線上的 × 點(diǎn)(實(shí)際上想要達(dá)到的點(diǎn))。為什么?因?yàn)檫@是一個(gè)鞍點(diǎn)(saddle point)。同樣要注意的是,當(dāng)我們調(diào)整α?xí)r會(huì)發(fā)生什么。我們可以觀察到,相對(duì)于其他解,一個(gè)解需要調(diào)整多少個(gè)起點(diǎn),但我們無法調(diào)整以找到帕累托前沿面上的其他解。第一,即使沒有引入超參數(shù)來權(quán)衡損失,說梯度下降試圖在反作用力之間保持平衡也是不正確的。根據(jù)模型可實(shí)現(xiàn)的解,可以完全忽略其中一種損失,而將注意力放在另一種損失上,反之亦然,這取決于初始化模型的位置;
第二,即使引入了超參數(shù),也將在嘗試后的基礎(chǔ)上調(diào)整此超參數(shù)。研究中往往是運(yùn)行一個(gè)完整的優(yōu)化過程,然后確定是否滿意,再對(duì)超參數(shù)進(jìn)行微調(diào)。重復(fù)此優(yōu)化循環(huán),直到對(duì)性能滿意為止。這是一種費(fèi)時(shí)費(fèi)力的方法,通常涉及多次運(yùn)行梯度下降的迭代;
第三,超參數(shù)不能針對(duì)所有的最優(yōu)情況進(jìn)行調(diào)整。無論進(jìn)行多少調(diào)整和微調(diào),你都不會(huì)找到可能感興趣的中間方案。這不是因?yàn)樗鼈儾淮嬖冢鼈円欢ù嬖冢皇且驗(yàn)檫x擇了一種糟糕的組合損失方法;
第四,必須強(qiáng)調(diào)的是,對(duì)于實(shí)際應(yīng)用,帕累托前沿面是否為凸面以及因此這些損失權(quán)重是否可調(diào)始終是未知的。它們是否是好的超參數(shù),取決于模型的參數(shù)化方式及其影響帕累托曲線的方式。但是,對(duì)于任何實(shí)際應(yīng)用,都無法可視化或分析帕累托曲線。可視化比原始的優(yōu)化問題要困難得多。因此出現(xiàn)問題并不會(huì)引起注意;
最后,如果你真的想使用這些線性權(quán)重來進(jìn)行權(quán)衡,則需要明確證明整個(gè)帕累托曲線對(duì)于正在使用的特定模型是凸的。因此,使用相對(duì)于模型輸出而言凸的損失不足以避免問題。如果參數(shù)化空間很大(如果優(yōu)化涉及神經(jīng)網(wǎng)絡(luò)內(nèi)部的權(quán)重,則情況總是如此),你可能會(huì)忘記嘗試這種證明。需要強(qiáng)調(diào)的是,基于某些中間潛勢(shì)(intermediate latent),顯示這些損失的帕累托曲線的凸度不足以表明你具有可調(diào)參數(shù)。凸度實(shí)際上需要取決于參數(shù)空間以及可實(shí)現(xiàn)解決方案的帕累托前沿面。
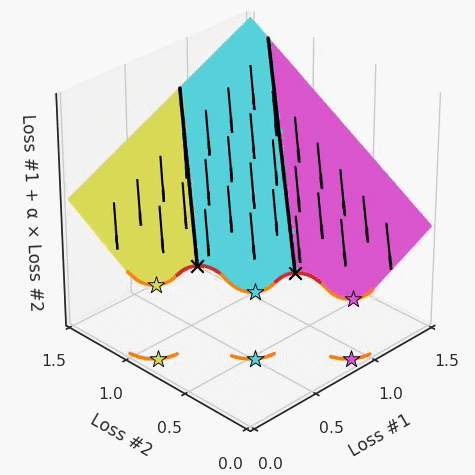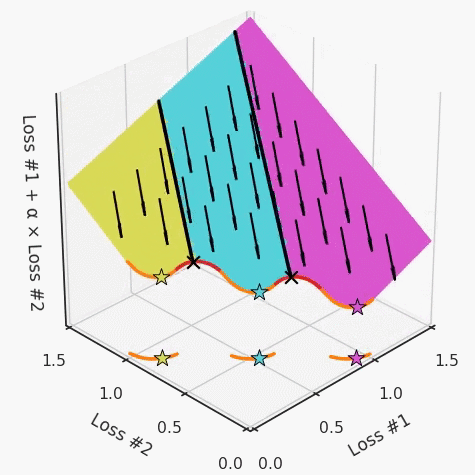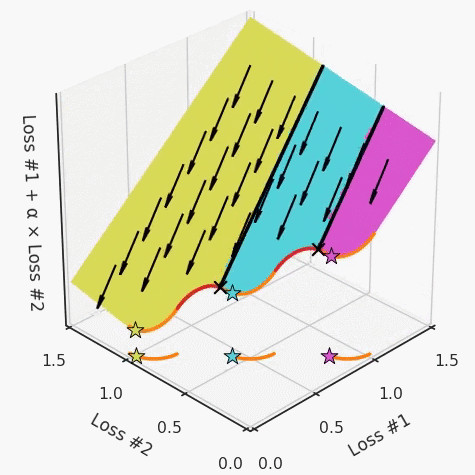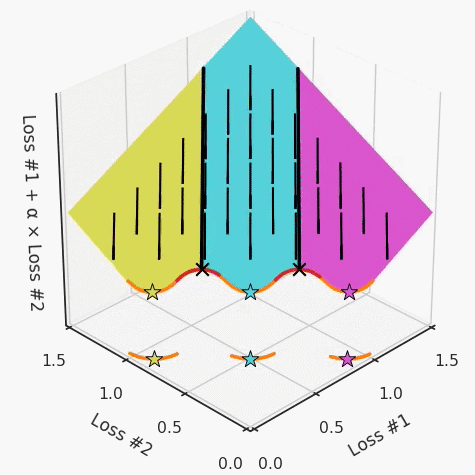
請(qǐng)注意,在大多數(shù)應(yīng)用中,帕累托前沿面既不是凸的也不是凹的,而是二者的混合體,這擴(kuò)大了問題。以一個(gè)帕累托前沿面為例,凸塊之間有凹?jí)K。每個(gè)凹?jí)K不僅可以確保無法通過梯度下降找到解,還可以將參數(shù)初始化的空間分成兩部分,一部分可以在一側(cè)的凸塊上找到解,而另一部分智能在另一側(cè)上找到解。如下動(dòng)圖所示,在帕累托前沿面上有多個(gè)凹?jí)K會(huì)使問題更加復(fù)雜。因此,我們不僅具有無法找到所有解的超參數(shù)α,而且根據(jù)初始化,它可能會(huì)找到帕累托曲線的不同凸部分。此參數(shù)和初始化以令人困惑的方式相互混合,這讓問題更加困難。如果稍微調(diào)整參數(shù)以希望稍微移動(dòng)最優(yōu)值,則即使保持相同的初始化,也可能會(huì)突然跳到帕累托前沿面的其他凸部分。https://engraved.ghost.io/why-machine-learning-algorithms-are-hard-to-tune/
編輯:黃繼彥
校對(duì):林亦霖