Hilbert 變換提取信號(hào)特征的 Python 實(shí)現(xiàn)

\hat{s}(t) ,則有: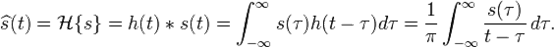
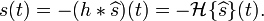
s(t),我們首先把它做一次希爾伯特變換,然后提取特征值。(A-t)間的函數(shù)關(guān)系。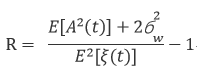

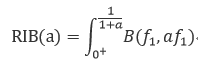
http://xueshu.baidu.com/usercenter/paper/show?paperid=f2c7b987bd3af320909da0e1c09a723b&site=xueshu_se,這篇論文,三種特征值能夠很好的表現(xiàn)信號(hào)性能。import?numpy?as?np?
from?math?import?pi?
import?matplotlib.pyplot?as?plt?
import?math?
from?scipy?import?fftpack?
from?sklearn?import?preprocessing?
import?neurolab?as?nl?
#碼元數(shù)?
size?=?10?
sampling_t?=?0.01?
t?=?np.arange(0,?size,?sampling_t)?
#隨機(jī)生成信號(hào)序列?
a?=?np.random.randint(0,?2,?size)??#產(chǎn)生隨機(jī)整數(shù)序列?
m?=?np.zeros(len(t),?dtype=np.float32)????#產(chǎn)生一個(gè)給定形狀和類型的用0填充的數(shù)組?
for?i?in?range(len(t)):?
????m[i]?=?a[int(math.floor(t[i]))]?
ts1?=?np.arange(0,?(np.int64(1/sampling_t)?*?size))/(10*(m+1))?
fsk?=?np.cos(np.dot(2?*?pi,?ts1)?+?pi?/?4)?
def?awgn(y,?snr):??????#snr為信噪比dB值?
????snr?=?10?**?(snr?/?10.0)?
????xpower?=?np.sum(y?**?2)?/?len(y)?
????npower?=?xpower?/?snr?
????return?np.random.randn(len(y))?*?np.sqrt(npower)?+?y?
def?feature_rj(y):????????#[feature1,?f2,?f3]?=?rj(noise_bpsk,?fs)?
????h?=?fftpack.hilbert(y)??#?hilbert變換?
????z?=?np.sqrt(y**2?+?h**2)??#?包絡(luò)?
????m2?=?np.mean(z**2)????#?包絡(luò)的二階矩?
????m4?=?np.mean(z**4)????#?包絡(luò)的四階矩?
????r?=?abs((m4-m2**2)/m2**2)?
????Ps?=?np.mean(y**2)/2?
????j?=?abs((m4-2*m2**2)/(4*Ps**2))?
????return?(r,j)?
def?feature_Bispectrum(y):?
????ly?=?size??#?行數(shù)10?
????nrecs?=?np.int64(1?/?sampling_t)??#?列數(shù)100?
????nlag?=?20?
????nsamp?=?nrecs??#?每段樣本數(shù)100?
????nrecord?=?size?
????nfft?=?128?
????Bspec?=?np.zeros((nfft,?nfft),?dtype=np.float32)?
????y?=?y.reshape(ly,?nrecs)?
????c3?=?np.zeros((nlag?+?1,?nlag?+?1),?dtype=np.float32)?
????ind?=?np.arange(nsamp)?
????for?k?in?range(nrecord):?
????????x?=?y[k][ind]?
????????x?=?x?-?np.mean(x)?
????????for?j?in?range(nlag?+?1):?
????????????z?=?np.multiply(x[np.arange(nsamp?-?j)],?x[np.arange(j,?nsamp)])?
????????????for?i?in?range(j,?nlag?+?1):?
????????????????sum?=?np.mat(z[np.arange(nsamp?-?i)])?*?np.mat(x[np.arange(i,?nsamp)]).T?
????????????????sum?=?sum?/?nsamp?
????????????????c3[i][j]?=?c3[i][j]?+?sum??#?i,j順序?
????c3?=?c3?/?nrecord?
????c3?=?c3?+?np.mat(np.tril(c3,?-1)).T??#?取對(duì)角線以下三角,c3為矩陣?
????c31?=?c3[1:,?1:]?
????c32?=?np.mat(np.zeros((nlag,?nlag),?dtype=np.float32))?
????c33?=?np.mat(np.zeros((nlag,?nlag),?dtype=np.float32))??#?不可以直接3者相等?
????c34?=?np.mat(np.zeros((nlag,?nlag),?dtype=np.float32))?
????for?i?in?range(nlag):?
????????x?=?c31[i:,?i]?
????????c32[nlag?-?1?-?i,?0:nlag?-?i]?=?x.T?
????????c34[0:nlag?-?i,?nlag?-?1?-?i]?=?x?
????????if?i?1):?
????????????x?=?np.flipud(x[1:,?0])??#?上下翻轉(zhuǎn),翻轉(zhuǎn)后依然為矩陣?
????????????c33?=?c33?+?np.diag(np.array(x)[:,?0],?i?+?1)?+?np.diag(np.array(x)[:,?0],?-(i?+?1))?
????c33?=?c33?+?np.diag(np.array(c3)[0,?:0:-1])?
????cmat?=?np.vstack((np.hstack((c33,?c32,?np.zeros((nlag,?1),?dtype=np.float32))),?
??????????????????????np.hstack((np.vstack((c34,?np.zeros((1,?nlag),?dtype=np.float32))),?c3))))??????????#41*41?
????Bspec?=?fftpack.fft2(cmat,?[nfft,?nfft])?????
????Bspec?=?np.fft.fftshift(Bspec)????????????????#128*128?
????waxis?=?np.arange(-nfft?/?2,?nfft?/?2)?/?nfft?
????X,?Y?=?np.meshgrid(waxis,?waxis)?
????plt.contourf(X,?Y,?abs(Bspec),alpha=0,cmap=plt.cm.hot)?
????plt.contour(X,?Y,?abs(Bspec))?
????plt.show()?
????return?Bspec?
def?features(s):?
#????for?mc?in?range(2):?
????????snr?=?np.random.uniform(0,?20)??????#從一個(gè)均勻分布集合中隨機(jī)采樣,左閉右開(kāi)--[low,high)?
????????s?=?awgn(s,snr)????????????#在原始信號(hào)的基礎(chǔ)上增加SNR信噪比的噪音?
????????rj?=?np.array(feature_rj(s))??????????????#計(jì)算R,J特征?
????????z?=?feature_Bispectrum(s)??????????????????#計(jì)算雙譜特征,并畫圖像?
????????xx?=?np.int64(np.sqrt(np.size(z))/2)?
????????z?=?np.array(z[:xx,xx:])?
????????z?=?np.tril(z).real??????????????#取復(fù)數(shù)z的實(shí)部?
????????bis?=?np.zeros((1,?xx),dtype=np.float32)????#零組?
????????for?i?in?range(xx):?
????????????for?j?in?range(xx-i):?
????????????????bis[0][i]?=?bis[0][i]+z[xx-1-j][i+j]?
????????m?=?bis[0].reshape(1,xx)?
????????normalized?=?preprocessing.normalize(m)[0,:]????#樣本各個(gè)特征值除以各個(gè)特征值的平方之和?
????????features?=?np.hstack((rj,normalized))??????????#合并數(shù)組r,j和normalized?
????????return?features?
print(features(fsk))?
A,角頻率\omega ,初始頻率S的改變來(lái)說(shuō)明問(wèn)題。初始信號(hào)圖像如下: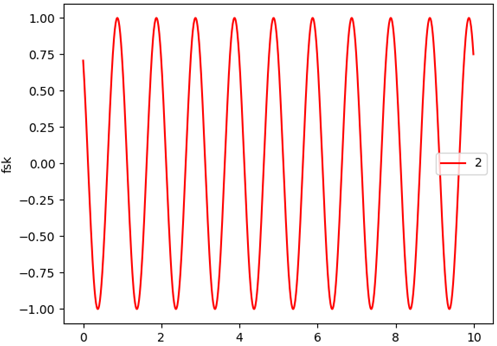
A,\omega ,S從0到2\Pi 均勻變化,對(duì)于振幅A的變化,補(bǔ)充代碼計(jì)算R,J特征值,畫出雙譜圖:R?=?[]
J?=?[]?
ts1?=?np.arange(0,?(np.int64(1/sampling_t)?*?size))/(10*(m+1))?
W?=?[]?
Z?=?[]?
for?i?in?range(0,40,1):?
????W.append(i?/?(2?*?pi))?
for?a1?in?W:?
????global?r,j?
????fsk?=?a1?*?np.cos(np.dot(2?*?pi,?ts1)?+?pi?/?4)?
????features(fsk)?
????R.append(r)?
????J.append(j)?
plt.plot(W,?R,?color='green',?label='1')?
plt.legend()?#?顯示圖例?
plt.xlabel('A[0-2?*?pi]')?
plt.ylabel('R')?
plt.show()?
plt.plot(W,?J,?color='red',?label='2')?
plt.legend()?#?顯示圖例?
plt.xlabel('A[0-2?*?pi]')?
plt.ylabel('J')?
plt.show()?
plt.plot(W,?Z,?color='red',?label='3')?
plt.legend()?#?顯示圖例?
plt.xlabel('A[0-2?*?pi]')?
plt.ylabel('trend')?
plt.show()?
R特征值變化圖像: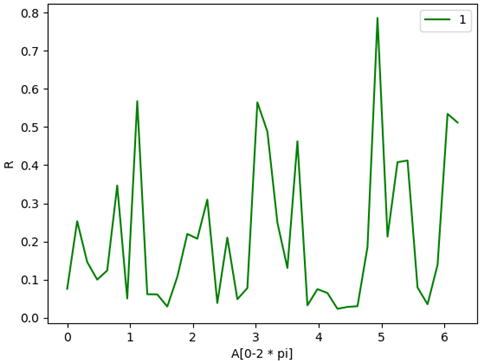
J特征值變化圖像: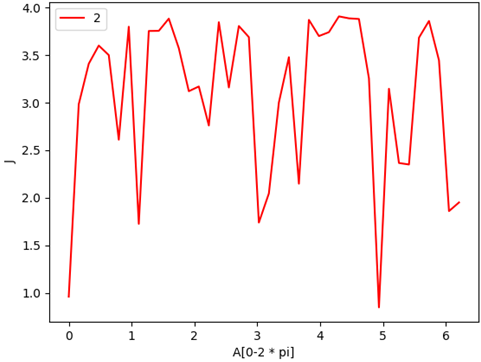
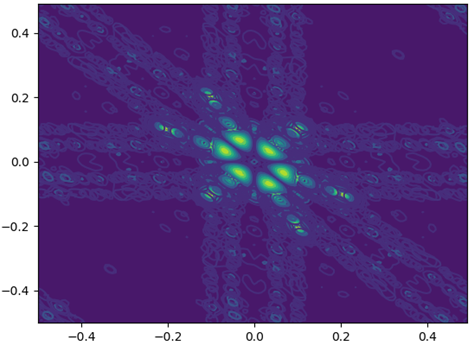
ω的變化,補(bǔ)充代碼計(jì)算R,J特征值,畫出R、J、雙譜圖像:R?=?[]
J?=?[]?
ts1?=?np.arange(0,?(np.int64(1/sampling_t)?*?size))/(10*(m+1))?
W?=?[]?
Z?=?[]?
for?i?in?range(0,40,1):?
????W.append(i?/?(2?*?pi))?
for?w?in?W:?
????global?r,j?
????fsk?=?np.cos(np.dot(w,?ts1)?+?pi?/?4)?
????features(fsk)?
????R.append(r)?
????J.append(j)?
plt.plot(W,?R,?color='green',?label='1')?
plt.legend()?#?顯示圖例?
plt.xlabel('w[0-2?*?pi]')?
plt.ylabel('R')?
plt.show()?
plt.plot(W,?J,?color='red',?label='2')?
plt.legend()?#?顯示圖例?
plt.xlabel('w[0-2?*?pi]')?
plt.ylabel('J')?
plt.show()?
plt.plot(W,?Z,?color='red',?label='3')?
plt.legend()?#?顯示圖例?
plt.xlabel('A[0-2?*?pi]')?
plt.ylabel('trend')?
plt.show()?
R特征值變化圖像: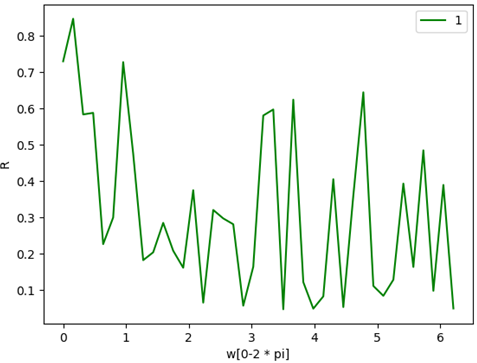
J特征值變化圖像:
S的變化,補(bǔ)充代碼計(jì)算R,J特征值,畫出雙譜圖:R?=?[]
J?=?[]?
ts1?=?np.arange(0,?(np.int64(1/sampling_t)?*?size))/(10*(m+1))?
W?=?[]?
Z?=?[]?
for?i?in?range(0,40,1):?
????W.append(i?/?(2?*?pi))?
for?s?in?W:?
????global?r,j?
????fsk?=?np.cos(np.dot(2?*?pi,?ts1)?+?s)?
????features(fsk)?
????R.append(r)?
????J.append(j)?
plt.plot(W,?R,?color='green',?label='1')?
plt.legend()?#?顯示圖例?
plt.xlabel('s[0-2?*?pi]')?
plt.ylabel('R')?
plt.show()?
plt.plot(W,?J,?color='red',?label='2')?
plt.legend()?#?顯示圖例?
plt.xlabel('s[0-2?*?pi]')?
plt.ylabel('J')?
plt.show()?
plt.plot(W,?Z,?color='red',?label='3')?
plt.legend()?#?顯示圖例?
plt.xlabel('A[0-2?*?pi]')?
plt.ylabel('trend')?
plt.show()?
R特征值變化圖像: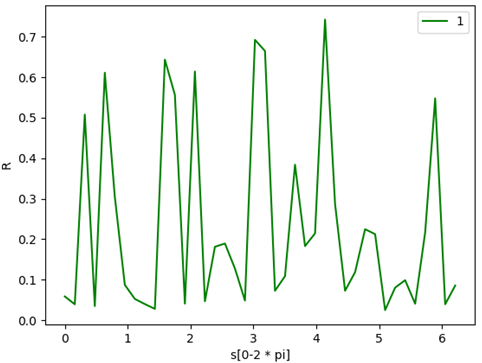
J特征值變化圖像: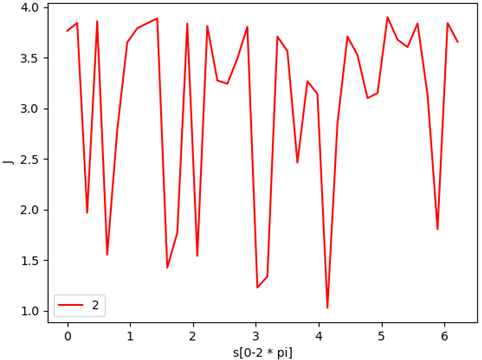

Bspec?=?fftpack.fft2(cmat,?[nfft,?nfft])
Bspec?=?np.fft.fftshift(Bspec)????????????????#128*128?
waxis?=?np.arange(-nfft?/?2,?nfft?/?2)?/?nfft?
X,?Y?=?np.meshgrid(waxis,?waxis)?
plt.contourf(X,?Y,?abs(Bspec))?
plt.contour(X,?Y,?abs(Bspec))?
Z.append(np.mean(abs(Bspec)))?
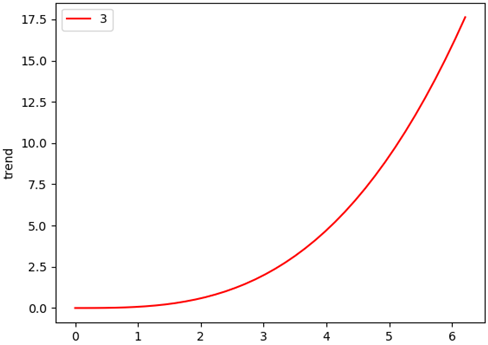
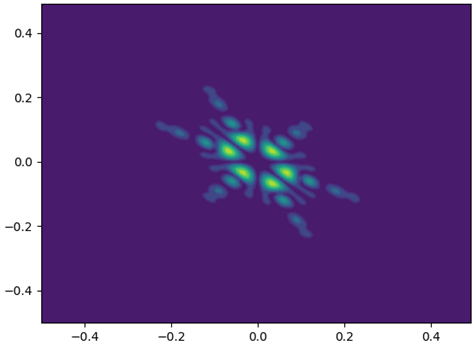
\omega 的雙譜特征變化情況: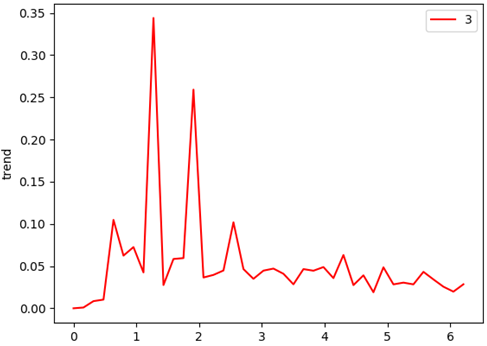
S的雙譜特征變化情況: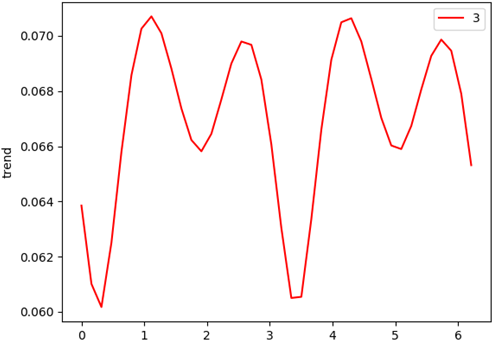
https://github.com/wangwei39120157028/Signal_Feature_Extraction/https://gitee.com/wwy2018/Signal_Feature_Extractionhttps://github.com/wangwei39120157028/IDAPythonScriptshttps://gitee.com/wwy2018/IDAPythonScripts更多閱讀
特別推薦

點(diǎn)擊下方閱讀原文加入社區(qū)會(huì)員
評(píng)論
圖片
表情
