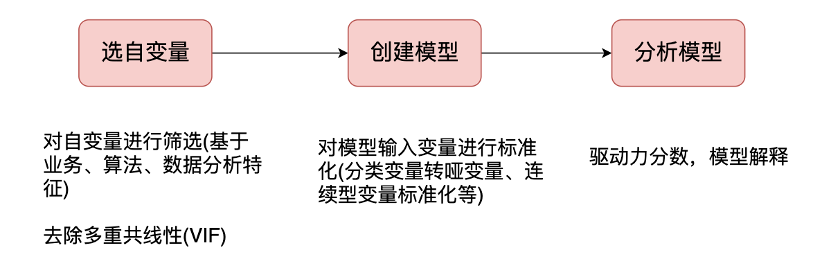
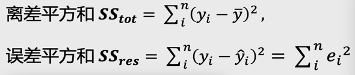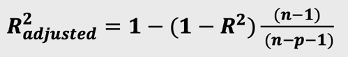很多同學(xué)目前所做的業(yè)務(wù)分析工作,徒手分析即可cover業(yè)務(wù)需求,較少用到一些高階的統(tǒng)計(jì)模型和機(jī)器學(xué)習(xí)上面的東西。漸漸的便會(huì)產(chǎn)生一種感覺(jué),即數(shù)據(jù)分析滿足業(yè)務(wù)需求即可,不需要會(huì)機(jī)器學(xué)習(xí)。
?1、目前的工作不需要,不代表之后的工作不需要,我們應(yīng)該著眼于我們整個(gè)數(shù)據(jù)分析生涯?;2、掌握一些模型可以高效做一些定量分析,較徒手分析效率更高,更準(zhǔn)?;3、我們覺(jué)得一些東西沒(méi)用,很可能是因?yàn)槲覀冞€沒(méi)有發(fā)現(xiàn)如何去用 ;4、我們對(duì)自己的要求不應(yīng)該止于滿足業(yè)務(wù)需求,一些探索性專題非常依賴于機(jī)器學(xué)習(xí) ;
基于以上,我嘗試開(kāi)始更新一些機(jī)器學(xué)習(xí)方面的文章,從較基礎(chǔ)的線性回歸、決策樹等開(kāi)始,希望大家可以跟著小洛一起學(xué)習(xí),有疑問(wèn)大家可以隨時(shí)在交流群提~
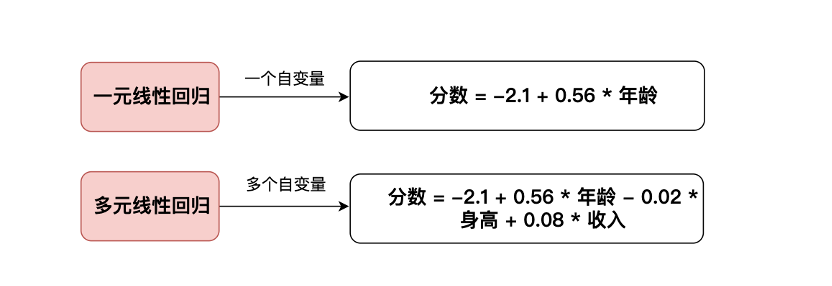
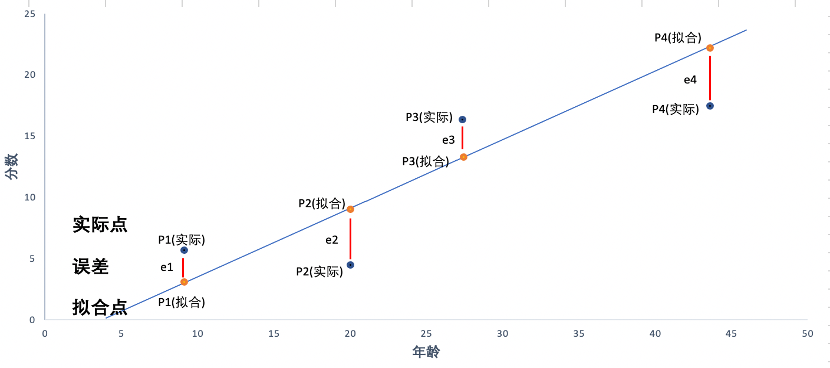
線性回歸是利用線性的方法,模擬因變量與一個(gè)或多個(gè)自變量之間的關(guān)系。對(duì)于模型而言,自變量是輸入值,因變量是模型基于自變量的輸出值,適用于x和y滿足線性關(guān)系的數(shù)據(jù)類型的應(yīng)用場(chǎng)景。線性回歸應(yīng)用于數(shù)據(jù)分析的場(chǎng)景主要有兩種:模型數(shù)學(xué)形式:?=?0+?1?1+?2?2+?+????例如要衡量不同的用戶特征對(duì)滿意分?jǐn)?shù)的影響程度,轉(zhuǎn)換成線性模型的結(jié)果可能就是:分?jǐn)?shù)=-2.1+0.56*年齡線性回歸模型分為一元線性回歸與多元線性回歸:區(qū)別在于自變量的個(gè)數(shù)我們知道了模型的公式,那么模型的系數(shù)是如何得來(lái)呢?我們用最小二乘法來(lái)確定模型的系數(shù)。最小二乘法,它通過(guò)最小化誤差的平方和尋找數(shù)據(jù)的最佳函數(shù)匹配,利用最小二乘法可以求得一條直線,并且使得擬合數(shù)據(jù)與實(shí)際數(shù)據(jù)之間誤差的平方和為最小。將上述模型公式簡(jiǎn)化成一個(gè)四個(gè)點(diǎn)的線性回歸模型來(lái)具體看:分?jǐn)?shù)=-2.1+0.56*年齡最小二乘法選取能使模型 誤差平方和= ??1?+ ?2?+ ?3?+ ?4?最小化的直線,生成直線后即可得出模型自變量的系數(shù)和截距。三、決定系數(shù)R方(R-squared)與調(diào)整R方
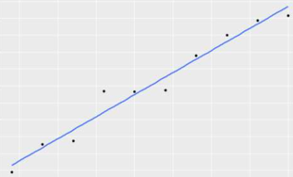
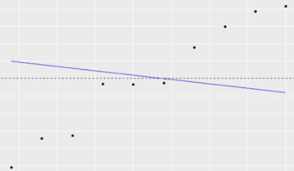
R方也叫決定系數(shù),它的主要作用是衡量數(shù)據(jù)中的因變量有多準(zhǔn)確可以被某一模型所計(jì)算解釋。公式:離差平方和:代表因變量的波動(dòng),即因變量實(shí)際值與其平均值之間的差值平方和誤差平方和:代表因變量實(shí)際值與模型擬合值之間的誤差大小故R方可以解釋因變量波動(dòng)中,被模型擬合的百分比,即R方可以衡量模型擬合數(shù)據(jù)的好壞程度;R方的取值范圍<=1,R方越大,模型對(duì)數(shù)據(jù)的擬合程度越好;使用不同模型擬合自變量與因變量之間關(guān)系的R方舉例,R方=1 模型完美的擬合數(shù)據(jù)(100%)R方=0.91 模型在一定程度較好的擬合數(shù)據(jù)(91%)
R方<0 擬合直線的趨勢(shì)與真實(shí)因變量相反
一般的R方會(huì)存在一些問(wèn)題,即把任意新的自變量加入到線性模型中,都可能會(huì)提升R方的值,模型會(huì)因加入無(wú)價(jià)值的變量導(dǎo)致R方提升,對(duì)最終結(jié)果產(chǎn)生誤導(dǎo)。故在建立多元線性回歸模型時(shí),我們把R方稍稍做一些調(diào)整,引進(jìn)數(shù)據(jù)量、自變量個(gè)數(shù)這兩個(gè)條件,輔助調(diào)整R方的取值,我們把它叫調(diào)整R方,調(diào)整R方值會(huì)因?yàn)樽宰兞總€(gè)數(shù)的增加而降低(懲罰),會(huì)因?yàn)樾伦宰兞繋?lái)的有價(jià)值信息而增加(獎(jiǎng)勵(lì));可以幫助我們篩選出更多有價(jià)值的新自變量。n:數(shù)據(jù)量大小(行數(shù))->數(shù)據(jù)量越大,新自變量加入所影響越小;p:自變量個(gè)數(shù)->自變量個(gè)數(shù)增加,調(diào)整R方變小,對(duì)這個(gè)量進(jìn)行懲罰;一句話,調(diào)整R方不會(huì)因?yàn)槟P托略鰺o(wú)價(jià)值變量而提升,而R方會(huì)因?yàn)槟P托略鰺o(wú)價(jià)值變量而提升!通過(guò)觀測(cè)調(diào)整R方可以在后續(xù)建模中去重多重共線性的干擾,幫助我們選擇最優(yōu)自變量組合。R方/調(diào)整R方值區(qū)間經(jīng)驗(yàn)判斷四、線性回歸在數(shù)據(jù)分析中的實(shí)戰(zhàn)流程我們以共享單車服務(wù)滿意分?jǐn)?shù)據(jù)為案例進(jìn)行模型實(shí)戰(zhàn),想要去分析不同的特征對(duì)滿意分的影響程度,模型過(guò)程如下:
1、讀取數(shù)據(jù)

2、切分因變量和自變量、分類變量轉(zhuǎn)換啞變量
多重共線性:就是在線性回歸模型中,存在一對(duì)以上強(qiáng)相關(guān)變量,多重共線性的存在,會(huì)誤導(dǎo)強(qiáng)相關(guān)變量的系數(shù)值。
強(qiáng)相關(guān)變量:如果兩個(gè)變量互為強(qiáng)相關(guān)變量,當(dāng)一個(gè)變量變化時(shí),與之相應(yīng)的另一個(gè)變量增大/減少的可能性非常大。
?
當(dāng)我們加入一個(gè)年齡強(qiáng)相關(guān)的自變量車齡時(shí),通過(guò)最小二乘法所計(jì)算得到的各變量系數(shù)如下,多重共線性影響了自變量車齡、年齡的線性系數(shù)。
這時(shí)候,可以使用VIF消除多重共線性:VIF=1/(1-R方),R方是拿其他自變量去線性擬合此數(shù)值變量y得到的線性回歸模型的決定系數(shù)。某個(gè)自變量造成強(qiáng)多重共線性判斷標(biāo)準(zhǔn)通常是:VIF>10
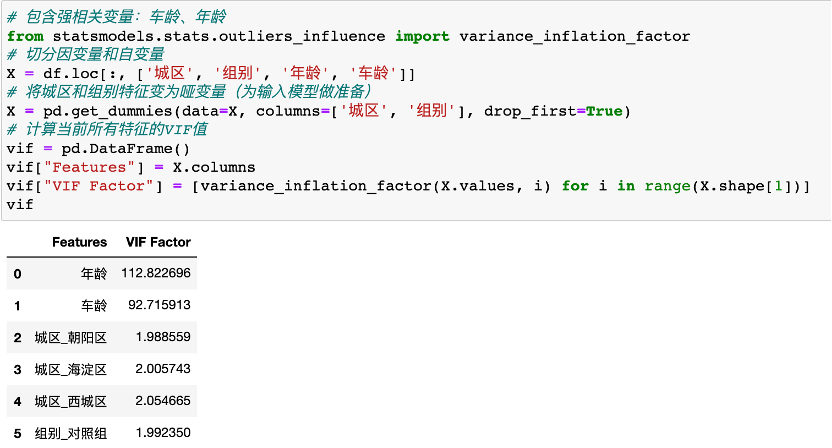
我們發(fā)現(xiàn),年齡的VIF遠(yuǎn)大于10,故去除年齡這一變量,去除后重新計(jì)算剩余變量VIF發(fā)現(xiàn)所有均<10,即可繼續(xù)。
4、計(jì)算調(diào)整R方

5、數(shù)據(jù)標(biāo)準(zhǔn)化
我們希望不同自變量的線性系數(shù),相互之間有可比性,不受它們?nèi)≈捣秶绊?/span>

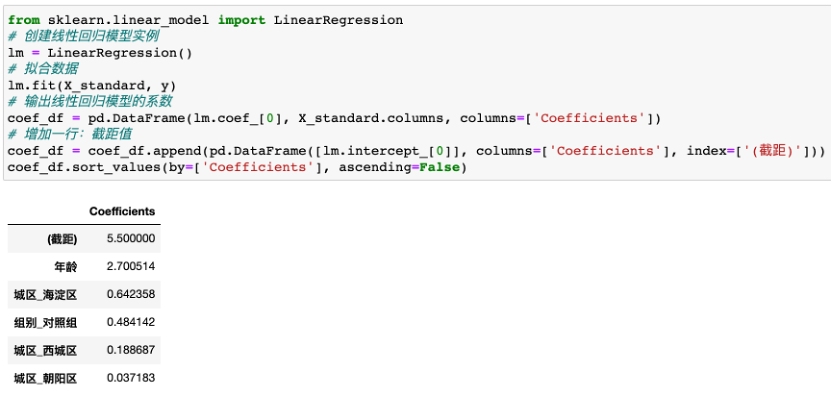
6、擬合模型,計(jì)算回歸系數(shù)
共享單車分?jǐn)?shù)案例,因變量是分?jǐn)?shù),自變量是年齡、組別、城區(qū),線性回歸的結(jié)果為:分?jǐn)?shù) = 5.5 + 2.7 * 年齡 +0.48 * 對(duì)照組 + 0.04 * 朝陽(yáng)區(qū) + 0.64 * 海淀區(qū) + 0.19 * 西城區(qū)
7、生成分析洞見(jiàn)-驅(qū)動(dòng)力因素??

最終產(chǎn)出不同用戶特征對(duì)用戶調(diào)研分?jǐn)?shù)的驅(qū)動(dòng)性排名。驅(qū)動(dòng)力分?jǐn)?shù)反應(yīng)各個(gè)變量代表因素,對(duì)目標(biāo)變量分?jǐn)?shù)的驅(qū)動(dòng)力強(qiáng)弱,驅(qū)動(dòng)力分?jǐn)?shù)絕對(duì)值越大,目標(biāo)變量對(duì)因素的影響力越大,反之越小,驅(qū)動(dòng)力分?jǐn)?shù)為負(fù)時(shí),表明此因素對(duì)目標(biāo)變量的影響為負(fù)向。
?
8、根據(jù)回歸模型進(jìn)行預(yù)測(cè)
至此,回歸模型已經(jīng)建好,預(yù)測(cè)就不寫了,把要預(yù)測(cè)的數(shù)據(jù)x自變量導(dǎo)入模型即可預(yù)測(cè)y。
--------? ?往 期 推 薦??----------? ??