如何用本福特分析模型發(fā)現(xiàn)問題?
你好,我是林驥。
上周有個讀者跟我說,建議在文章標題中寫上分析思維模型的名稱。
我覺得這個建議很好,在這篇文章的末尾處,增加了第 001 號至 013 號分析思維模型的名稱和鏈接,方便你選擇查看自己感興趣的模型。
據(jù)粗略估計,分析思維模型超過 100 種,但是按照二八法則,在實際工作中,常用的模型應(yīng)該不超過 20 種。
按照要事優(yōu)先的原則,我計劃在精選大約 20 種分析思維模型之后,開始考慮把重心放在模型的實踐應(yīng)用上面。以后再根據(jù)實際情況,適當進行增加和補充,這將是一個長期的過程。
今天介紹第 014 號分析思維模型:本福特分析模型。
1. 模型介紹
20 世紀 20 年代,物理學(xué)家弗蘭克·本福特發(fā)現(xiàn),科學(xué)研究和工程設(shè)計中遇到的數(shù)據(jù),有 30% 左右都以 1 為首位數(shù)。
此后 10 年,本福特堅持不懈地探索這個現(xiàn)象,通過舉一反三,發(fā)現(xiàn)更多符合該規(guī)律的數(shù)據(jù),比如網(wǎng)球得分、股票價格、河流長度、原子量、電費單等等,全都有著相同的模式。
本福特這種孜孜不倦的精神,值得我們學(xué)習(xí)。
1938 年,他推導(dǎo)出一套精確的計算公式:
其中 = 1~9,根據(jù)這個公式,就能計算出每個首位數(shù)的比例如下:
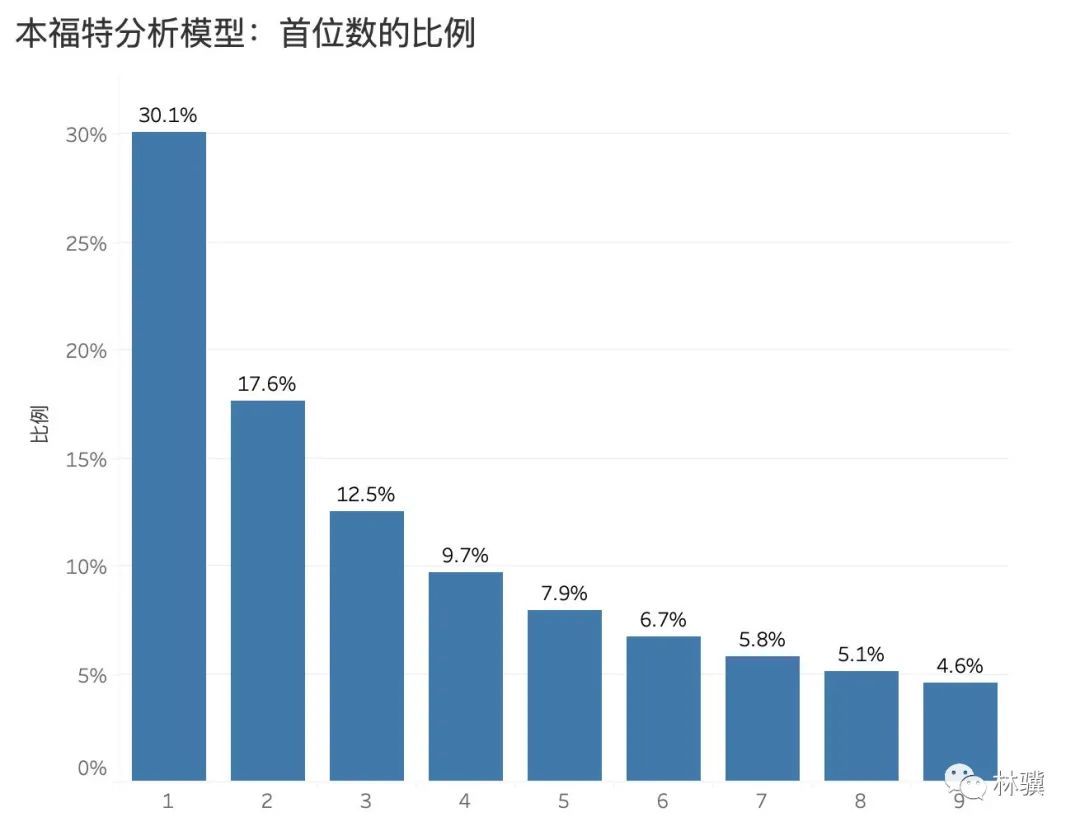
本福特是以非零數(shù)字為首位數(shù),所以 0 不包括在內(nèi),例如 126 和 0.0126 的第一個數(shù)字都是 1。
需要注意的是,有些數(shù)據(jù)并不適用于本福特定律,例如:電話號碼、郵政編碼、年齡、體重、智商,等等。
2. 應(yīng)用舉例
下面以 Tableau 自帶的世界指標數(shù)據(jù)為例,驗證世界各地區(qū)的 GDP 首位數(shù)是否符合本福特分析模型。
(1)打開 Tableau 自帶的【世界發(fā)展指標】數(shù)據(jù)
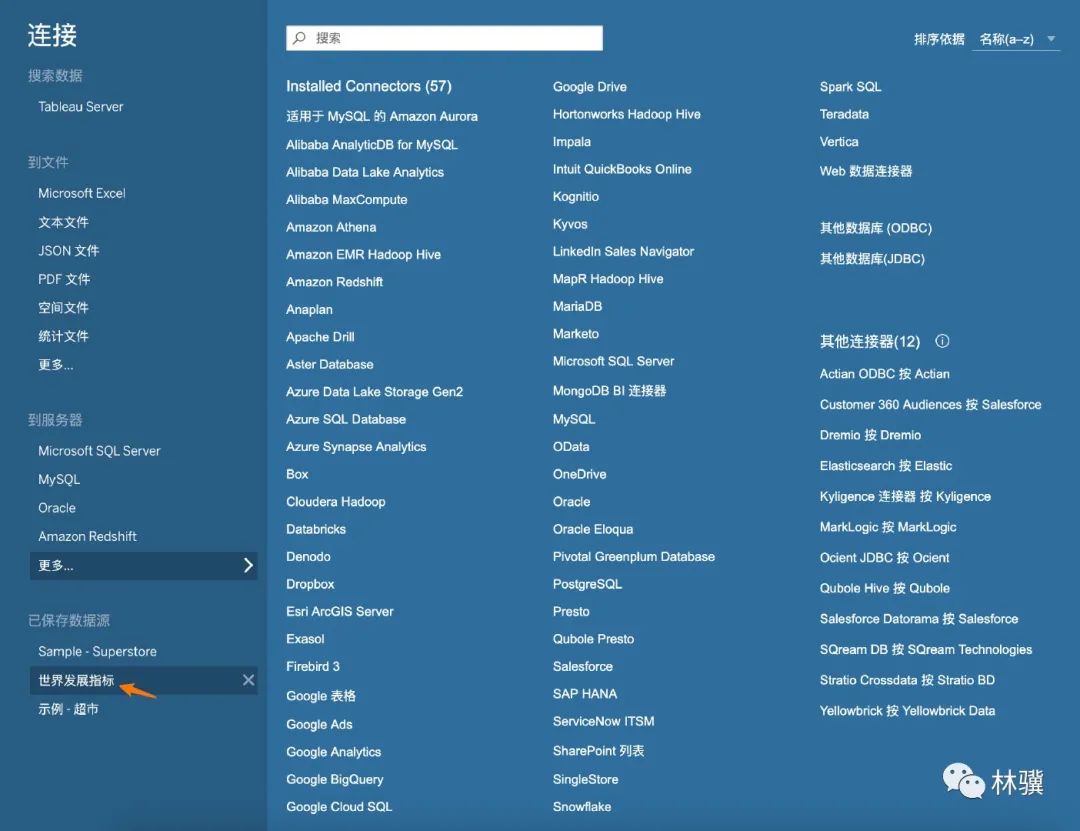
(2)創(chuàng)建計算字段【GDP首位數(shù)】,輸入公式:LEFT(STR([GDP]),1)
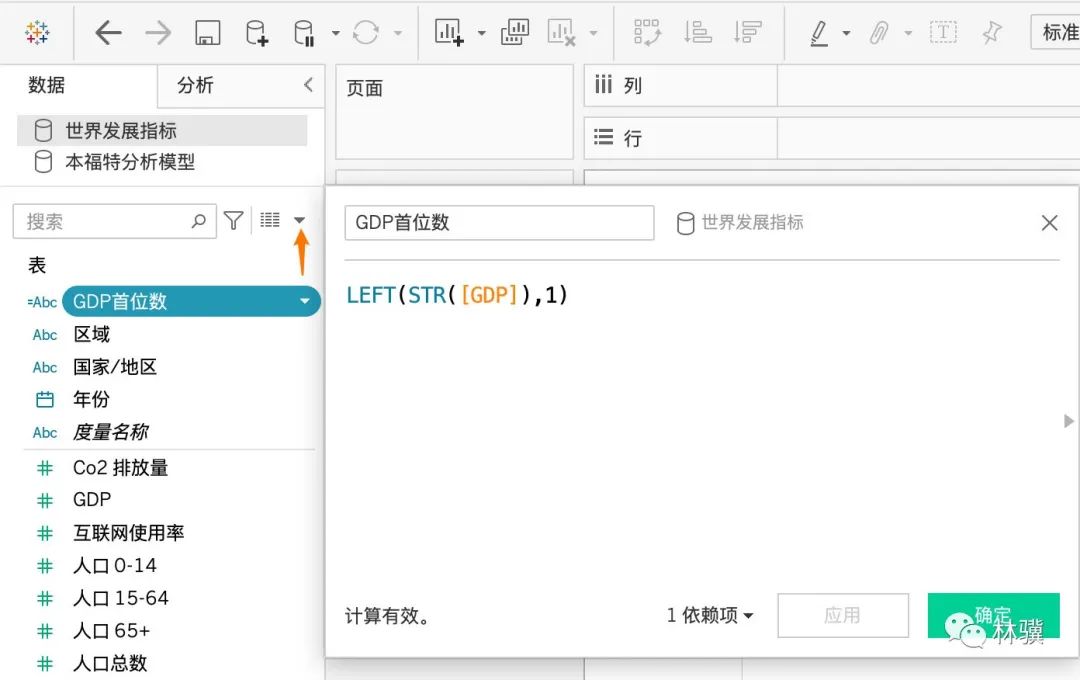
(3)把【GDP首位數(shù)】拖至【列】,把【記錄數(shù)】拖至【行】,下拉選擇【快速表計算】--【合計百分比】,在【篩選器】中排除 Null 值之后,得到 GDP 首位數(shù)的比例分布如下:
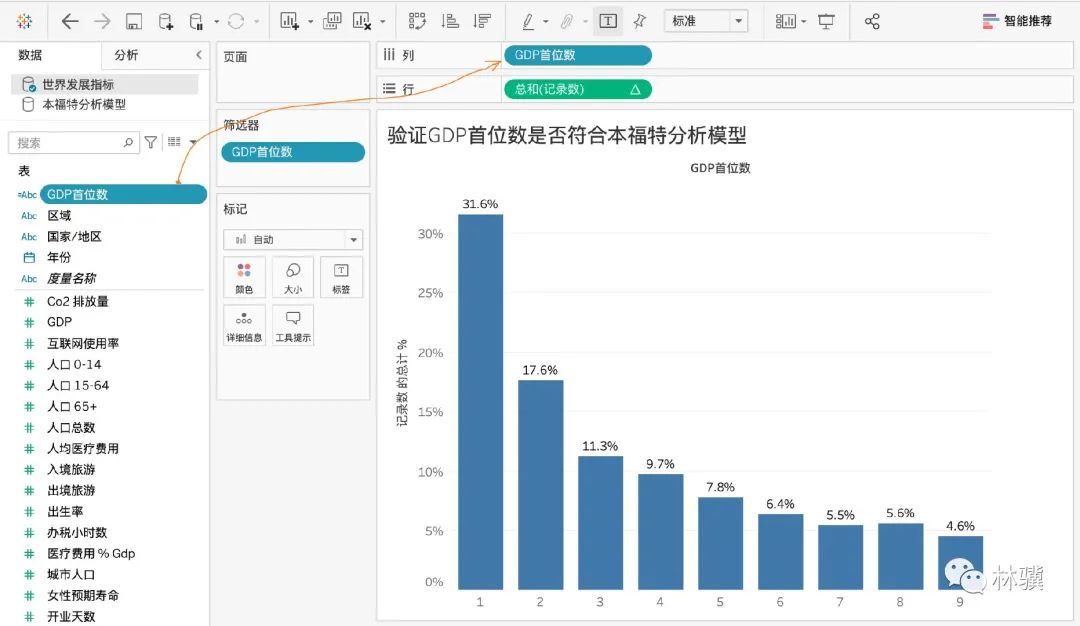
可以看出,世界各地區(qū)的 GDP 數(shù)據(jù)基本符合本福特分析模型。
(4)為了更加直觀地進行驗證,我們創(chuàng)建一個計算字段【本福特參考比例】,輸入公式:LOG(1+1/INT([GDP首位數(shù)]))
(5)把【本福特參考比例】拖到【詳細信息】標記中,更改度量為【平均值】。
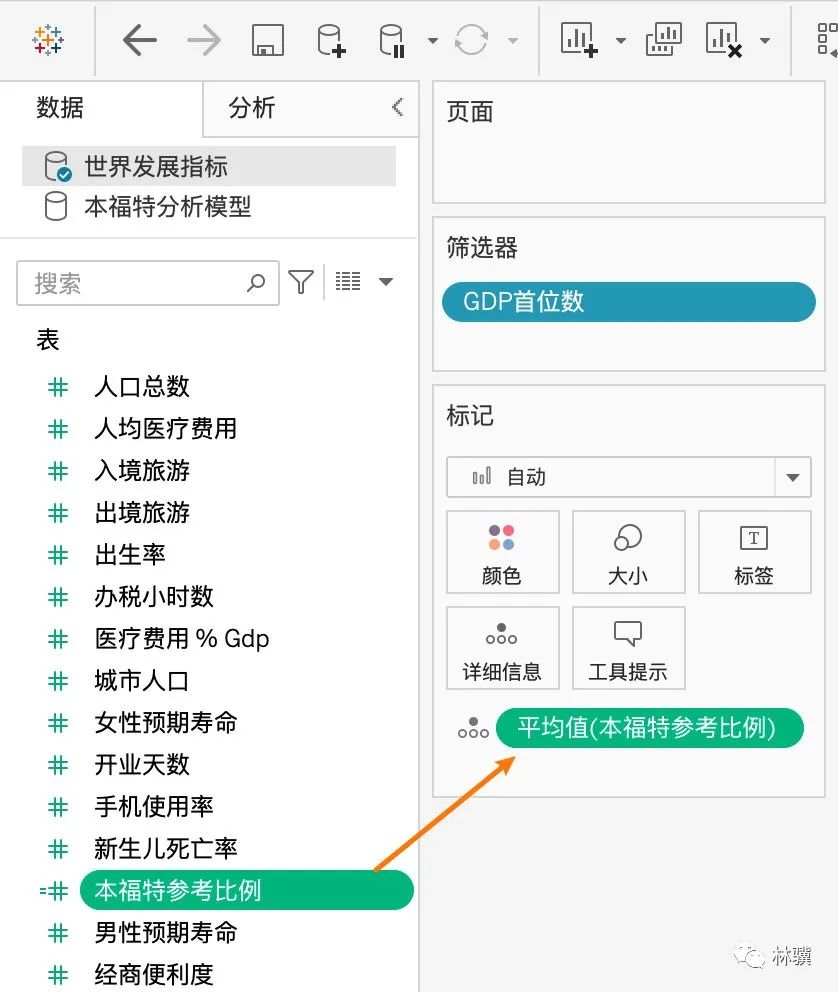
(6)切換到【分析】窗格,把【分布區(qū)間】拖到畫布的【單元格】中。
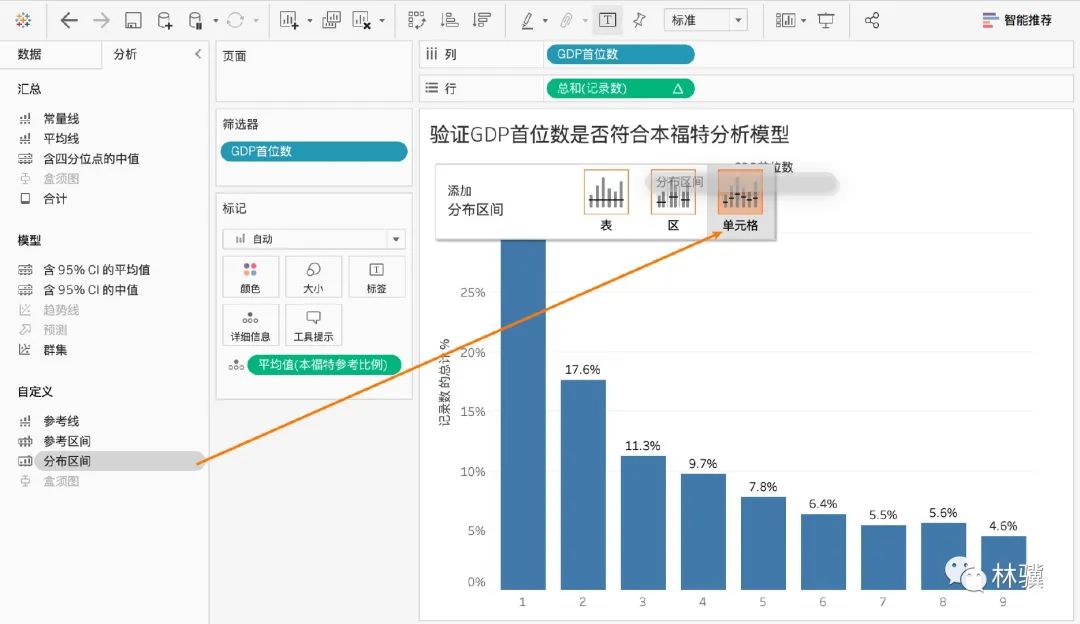
(7)把【計算-值】中的百分比改成 80,100,120,并選擇【平均值(本福特參考比例)】。
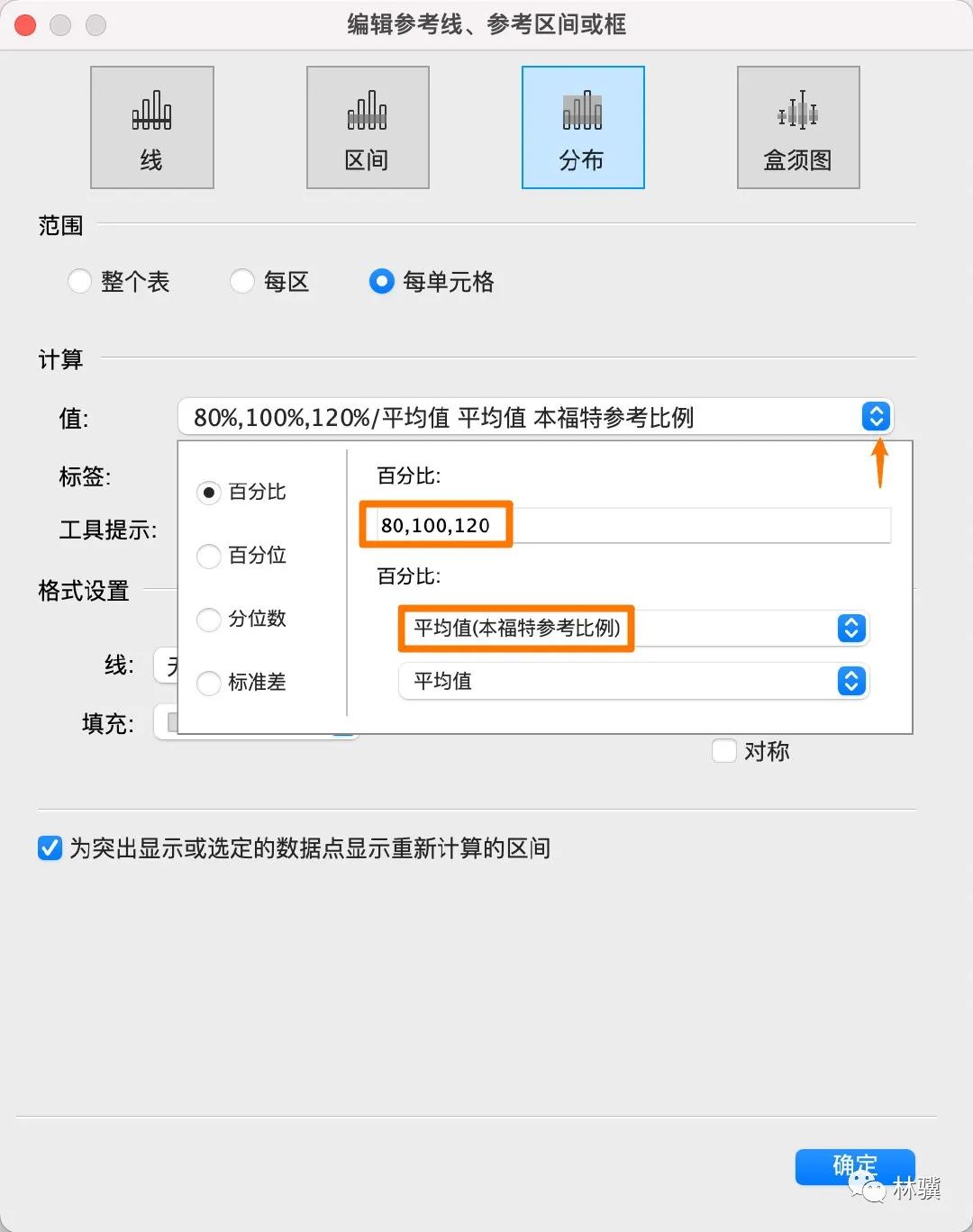
(8)設(shè)置參考區(qū)間的格式,標簽和線設(shè)置為【無】,向下填充為【藍色】。
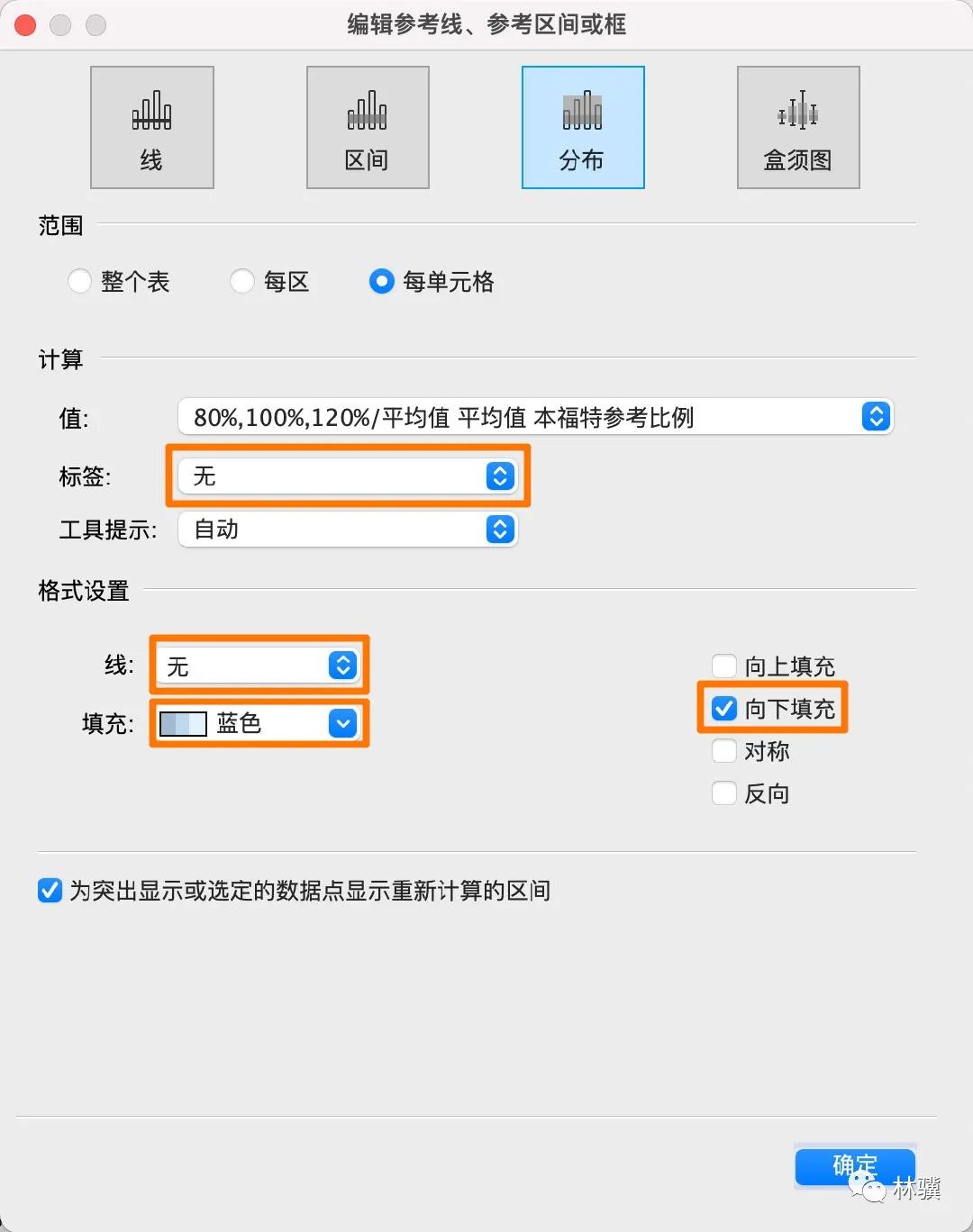
(9)點擊確定后,可以看出,GDP 首位數(shù)的比例,均介于本福特參考比例的 80% ~ 120% 之間。
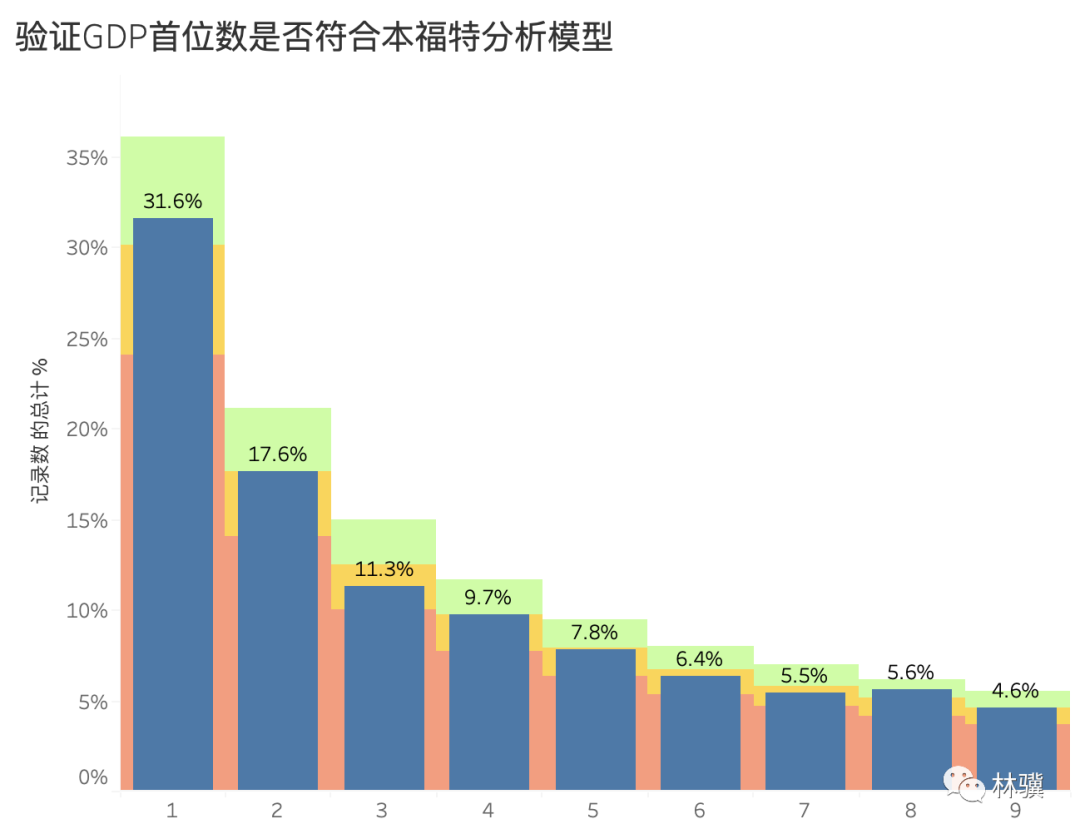
本福特分析模型可以用來發(fā)現(xiàn)問題,但并不能以此作為確鑿的證據(jù),因為本福特分析模型只是統(tǒng)計上的一種規(guī)律,并沒有經(jīng)過嚴格的證明,而且有其適用的范圍。
比如說,跨度較小的數(shù)據(jù)一般不符合本福特分析模型。
在世界指標數(shù)據(jù)中有一列:開業(yè)天數(shù),最大值不超過 700 天,按照上面的步驟,首位數(shù)分布如下:
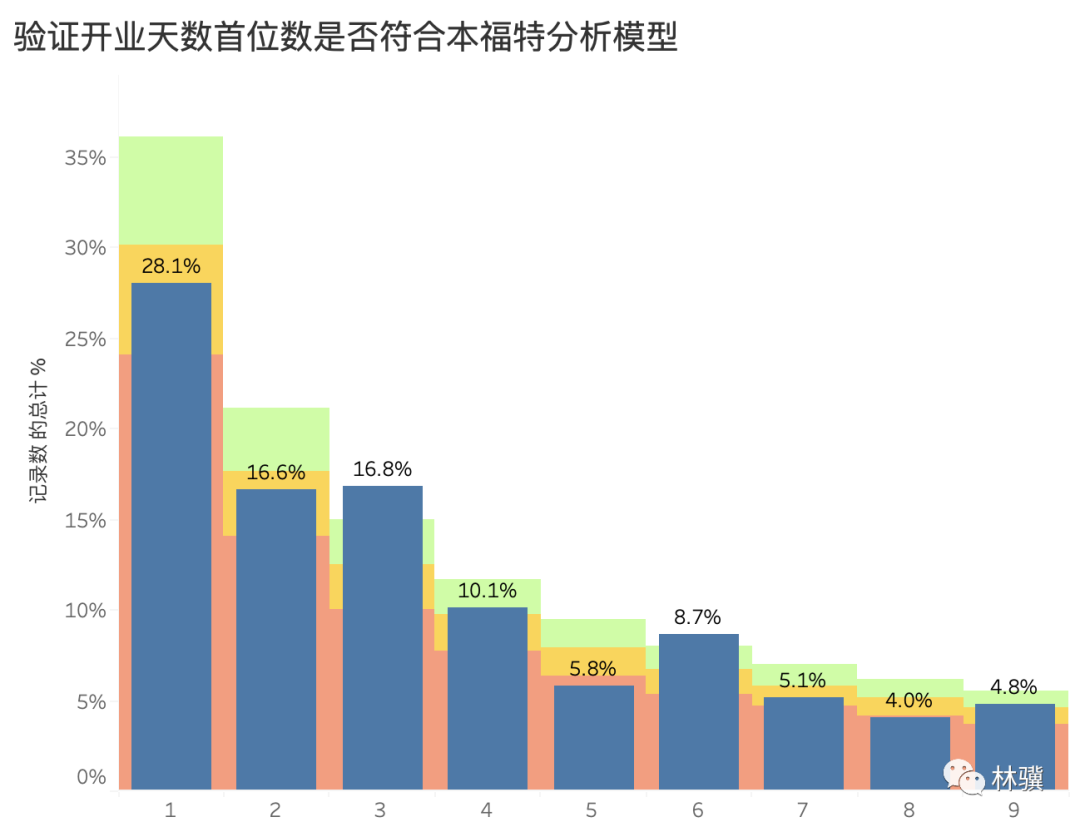
可以看出,其中數(shù)字 3、5、6 都不符合本福特分析模型。
利用本福特分析模型,我們可以發(fā)現(xiàn)可疑的數(shù)據(jù),通過大膽假設(shè),小心求證,探究數(shù)據(jù)背后隱藏的信息,從而幫助我們更好地解決問題。
雖然本福特分析模型目前無法確鑿地證明,但是先發(fā)現(xiàn)一些數(shù)據(jù)的規(guī)律,然后再來找到數(shù)據(jù)背后可能的原因,而這正是模型的力量和魅力所在。
比如說,對于上市公司的財務(wù)數(shù)據(jù),我們可以應(yīng)用本福特分析模型去驗證一下,如果發(fā)現(xiàn)首位數(shù)的比例嚴重偏離模型,那么就有理由去懷疑財務(wù)數(shù)據(jù)造假,再通過調(diào)查取證等方法,去驗證我們的假設(shè)。
最后的話
分析思維模型,是對現(xiàn)實世界的抽象和簡化,它的價值是能夠重新定義問題,從而找到更高效的解決方案。
統(tǒng)計學(xué)家喬治·博克斯有一句名言:所有的模型都是錯誤的,但有些是有用的。
應(yīng)用分析思維模型的時候,我們要保持警惕,不要被數(shù)據(jù)或模型所誤導(dǎo)。
如果數(shù)據(jù)或模型應(yīng)用不當,那么就像開車時看一個不準的儀表盤,對司機來說,錯誤的速度數(shù)據(jù),比沒有數(shù)據(jù)更危險,后果不堪設(shè)想。
如果數(shù)據(jù)和模型應(yīng)用得當,那么就像看病時配備先進的儀器,利用正確的數(shù)據(jù)和經(jīng)驗,能幫助我們找到真正的病因。
犯錯并不在于數(shù)據(jù)或模型本身,而在于使用數(shù)據(jù)和模型的人。
數(shù)據(jù)和模型的意義,并不是進行無數(shù)次高深的數(shù)學(xué)計算,而是在于更好地洞察現(xiàn)象背后的成因。
看完《人生算法》的序言之后,我相信:只要是能夠量化的事物,就能用算法和分析思維模型去優(yōu)化它。
用分析的視角、概率的思維、模型的算法,去解決工作和生活中的各種難題,這是我正在探索的一條路。
努力去做那些大概率對人生有益的事,比如讀書、寫作、利他。
避開那些小概率但致命的風(fēng)險,比如賭博、飆車、害人。