?【機(jī)器學(xué)習(xí)】數(shù)據(jù)科學(xué)中 17 種相似性和相異性度量(下)

⑦ 皮爾遜相關(guān)距離

相關(guān)距離量化了兩個(gè)屬性之間線性、單調(diào)關(guān)系的強(qiáng)度。此外，它使用協(xié)方差值作為初始計(jì)算步驟。但是，協(xié)方差本身很難解釋，并且不會(huì)顯示數(shù)據(jù)與表示測(cè)量之間趨勢(shì)的線的接近或遠(yuǎn)離程度。

為了說明相關(guān)性意味著什么，回到我們的 Iris 數(shù)據(jù)集并繪制?Iris-Setosa?樣本以顯示兩個(gè)特征之間的關(guān)系：花瓣長(zhǎng)度和花瓣寬度。

已估計(jì)相同花卉樣本的兩個(gè)特征的樣本均值和方差，如下圖所示。

一般來說，我們可以說花瓣長(zhǎng)度值相對(duì)較低的花的花瓣寬度值也相對(duì)較低。此外，花瓣長(zhǎng)度值相對(duì)較高的花朵也具有花瓣寬度值相對(duì)較高的值。此外，我們可以用一條線來總結(jié)這種關(guān)系。

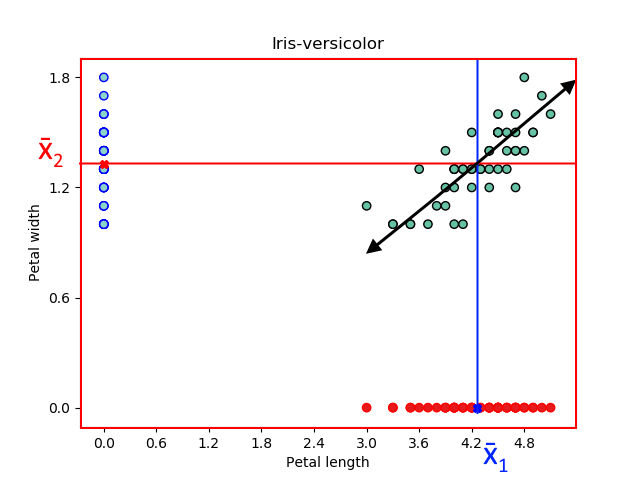
這條線表示花瓣長(zhǎng)度和花瓣寬度的值一起增加的積極趨勢(shì)。

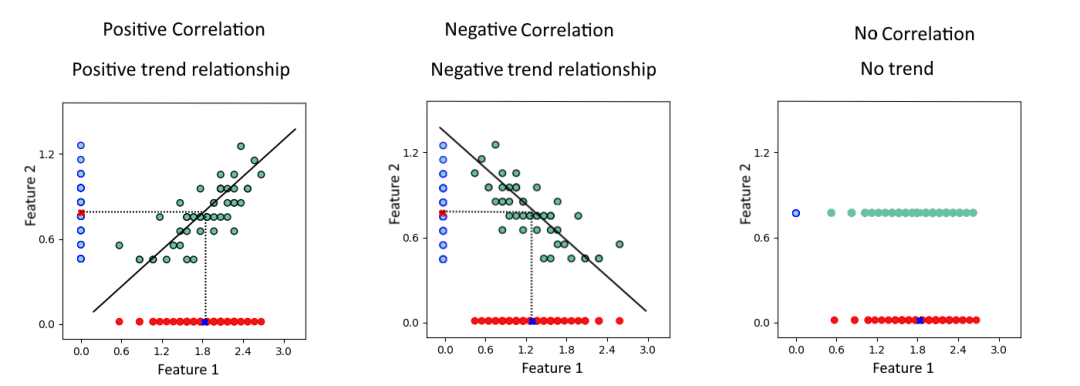
協(xié)方差值可以對(duì)三種關(guān)系進(jìn)行分類：

相關(guān)距離可以使用以下公式計(jì)算：

其中分子表示觀測(cè)值的協(xié)方差值，分母表示每個(gè)特征方差的平方根。

舉一個(gè)簡(jiǎn)單的例子來演示我們?nèi)绾斡?jì)算這個(gè)公式。

紅點(diǎn)和藍(lán)點(diǎn)分別具有以下坐標(biāo)：

A(1.2, 0.6) 和 B (3.0, 1.2)。

兩次測(cè)量的估計(jì)樣本均值等于：

該指標(biāo)的最后一點(diǎn)是相關(guān)性并不意味著因果關(guān)系。例如，具有相對(duì)較小花瓣長(zhǎng)度值的iris-Setosa?并不意味著花瓣寬度值也應(yīng)該較小。是充分條件但不是必要條件！可以說，小花瓣長(zhǎng)度可能導(dǎo)致小花瓣寬度，但不是唯一的原因！

⑧ 斯皮爾曼相關(guān)

與?Pearson?相關(guān)性一樣，每當(dāng)我們處理雙變量分析時(shí)，都會(huì)使用?Spearman?相關(guān)性。但是，與?Pearson?相關(guān)性不同，Spearman?相關(guān)性在兩個(gè)變量都按等級(jí)排序時(shí)使用，它可用于分類和數(shù)字屬性。

斯皮爾曼相關(guān)指數(shù)可以使用以下公式計(jì)算：

Spearman 相關(guān)性常用于假設(shè)檢驗(yàn)。

⑨ 馬氏距離

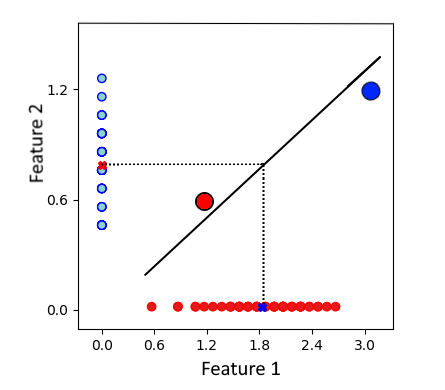
馬氏距離Mahalanobis是一種主要用于多變量統(tǒng)計(jì)測(cè)試的度量指標(biāo)，其中歐氏距離無法給出觀測(cè)值之間的實(shí)際距離。它測(cè)量數(shù)據(jù)點(diǎn)離分布有多遠(yuǎn)。

來自平均值的具有相同 ED 值的兩個(gè)點(diǎn)。

如上圖所示，紅點(diǎn)和藍(lán)點(diǎn)與均值的歐幾里得距離相同。但是，它們不屬于同一區(qū)域或集群：紅點(diǎn)更有可能與數(shù)據(jù)集相似。但是藍(lán)色的被認(rèn)為是異常值，因?yàn)樗h(yuǎn)離代表數(shù)據(jù)集中最大可變性方向的線（長(zhǎng)軸回歸）。因此，引入了馬哈拉諾比斯度量來解決這個(gè)問題。

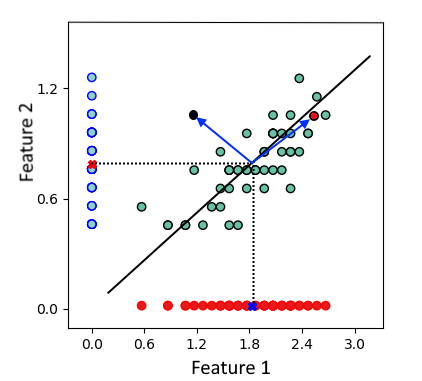
Mahalanobis 度量試圖降低兩個(gè)特征或?qū)傩灾g的協(xié)方差，因?yàn)槟梢詫⒅暗膱D重新縮放到新軸。并且這些新軸代表特征向量，如前面所示的第一個(gè)特征向量。

特征向量的第一個(gè)方向極大地影響了數(shù)據(jù)分類，因?yàn)樗哂凶畲蟮奶卣髦怠４送猓c其他垂直方向相比，數(shù)據(jù)集沿該方向展開得更多。

使用這種技術(shù)，我們可以沿著這個(gè)方向縮小數(shù)據(jù)集并圍繞均值（PCA）旋轉(zhuǎn)它。然后我們可以使用歐幾里得距離，它給出了與前兩個(gè)數(shù)據(jù)點(diǎn)之間的平均值的不同距離。這就是馬哈拉諾比斯指標(biāo)的作用。

兩個(gè)物體 P 和 Q 之間的馬氏距離。

其中C表示屬性或特征之間的協(xié)方差矩陣。

為了演示這個(gè)公式的用法，我們計(jì)算 A(1.2, 0.6) 和 B (3.0, 1.2) 之間的距離，來自之前在相關(guān)距離部分的例子。

現(xiàn)在評(píng)估協(xié)方差矩陣，其定義二維空間中的協(xié)方差矩陣如下：

其中 Cov[P,P] = Var[P] 和 Cov[Q,Q]= Var[Q]，以及兩個(gè)特征之間的協(xié)方差公式：

因此，兩個(gè)物體 A 和 B 之間的馬哈拉諾比斯距離可以計(jì)算如下：

除了其用例之外，馬哈拉諾比斯距離還用于Hotelling t 方檢驗(yàn)^[2]。

⑩ 標(biāo)準(zhǔn)化歐幾里得距離

標(biāo)準(zhǔn)化或歸一化是在構(gòu)建機(jī)器學(xué)習(xí)模型時(shí)在預(yù)處理階段使用的一種技術(shù)。該數(shù)據(jù)集在特征的最小和最大范圍之間存在很大差異。在對(duì)數(shù)據(jù)進(jìn)行聚類時(shí)，此比例距離會(huì)影響 ML 模型，從而導(dǎo)致錯(cuò)誤的解釋。

例如，假設(shè)有兩個(gè)不同的特征，它們?cè)诜秶兓矫姹憩F(xiàn)出很大差異。例如，假設(shè)有一個(gè)從 0.1 到 2 變化的特征和另一個(gè)從 50 到 200 變化的特征。使用這些值計(jì)算距離會(huì)使第二個(gè)特征更具優(yōu)勢(shì)，從而導(dǎo)致不正確的結(jié)果。換句話說，歐氏距離將受到具有最大值的屬性的高度影響。

這就是為什么標(biāo)準(zhǔn)化是必要的，以便這些特征以平等地做出貢獻(xiàn)。它是通過將變量轉(zhuǎn)換為所有具有等于 1 的相同方差并將特征集中在平均值周圍來完成的，如下面的公式所示 Z 分?jǐn)?shù)標(biāo)準(zhǔn)化：

標(biāo)準(zhǔn)化的歐幾里德距離可以表示為：

可以應(yīng)用這個(gè)公式來計(jì)算 A 和 B 之間的距離。

? 卡方距離

卡方距離通常用于計(jì)算機(jī)視覺中，同時(shí)進(jìn)行紋理分析，以發(fā)現(xiàn)歸一化直方圖之間的（不同）相似性，稱為“直方圖匹配”。

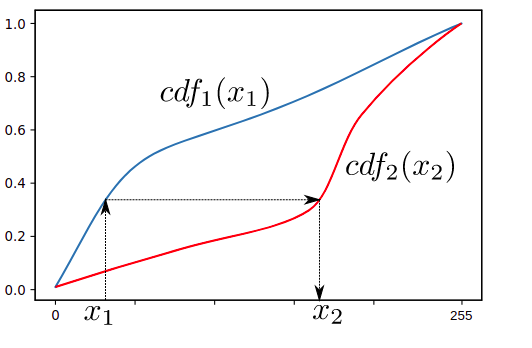
直方圖匹配。資料來源：維基百科直方圖匹配^[3]

人臉識(shí)別算法將是一個(gè)很好的例子，它使用這個(gè)指標(biāo)來比較兩個(gè)直方圖。例如，在新面孔的預(yù)測(cè)步驟中，模型根據(jù)新捕獲的圖像計(jì)算直方圖，將其與保存的直方圖（通常存儲(chǔ)在 .yaml 文件中）進(jìn)行比較，然后嘗試為其找到最佳匹配。這種比較是通過計(jì)算每對(duì) n 個(gè) bin 的直方圖之間的卡方距離來進(jìn)行的。

此公式與標(biāo)準(zhǔn)正態(tài)分布的卡方統(tǒng)計(jì)檢驗(yàn)不同，后者用于使用以下公式?jīng)Q定是保留還是拒絕原假設(shè)：

其中 O 和 E 分別代表觀察到的和預(yù)期的數(shù)據(jù)值。

假設(shè)對(duì) 1000 人進(jìn)行了一項(xiàng)調(diào)查，以測(cè)試給定疫苗的副作用，并查看是否存在基于性別的顯著差異。因此，每個(gè)人都可以是以下四類之一：

1-?男性無副作用。
2-?男性有副作用。
3-?女性無副作用。
4-?有副作用的女性。

零假設(shè)是：兩種性別之間的副作用沒有顯著差異。

為了接受或拒絕此假設(shè)，可以計(jì)算以下數(shù)據(jù)的卡方檢驗(yàn)值：

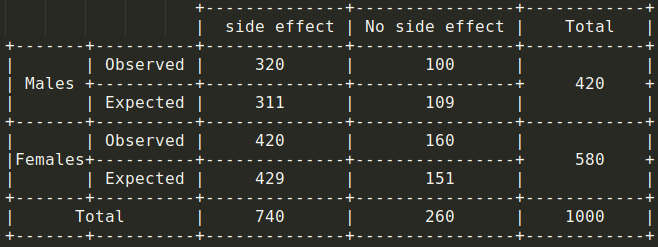
通過將這些值代入卡方檢驗(yàn)公式，將得到?1.7288。

使用自由度等于1的卡方表^[4]，將獲得介于 0.2 和 0.1 > 0.05 之間的概率 → 接受原假設(shè)。

請(qǐng)注意，自由度 =（列數(shù) -1）x（數(shù)量或行數(shù) -1）

這里只是想讓你快速回顧一下假設(shè)檢驗(yàn)；我希望你覺得這對(duì)你有幫助。

?Jensen-Shannon 距離

Jensen-Shannon 距離計(jì)算兩個(gè)概率分布之間的距離。它使用 Kullback Leibler divergence（相對(duì)熵）公式來計(jì)算距離。

Jensen-Shannon 距離。

其中 R 是 P 和 Q 之間的中點(diǎn)。

此外，只需簡(jiǎn)要說明如何解釋熵的值：

事件A的低熵意味著知道這個(gè)事件會(huì)發(fā)生；換句話說，如果事件 A 會(huì)發(fā)生，我并不感到驚訝，而且我非常有信心它會(huì)發(fā)生。高熵的類比相同。

另一方面，Kullback Leibler 散度本身不是距離度量，因?yàn)樗皇菍?duì)稱的：。

? 萊文斯坦距離

用于測(cè)量?jī)蓚€(gè)字符串之間相似性的度量。它等于將給定字符串轉(zhuǎn)換為另一個(gè)字符串所需的最少操作數(shù)。共有三種類型的操作：

1. 代換
2. 插入
3. 刪除

對(duì)于 Levenshtein 距離，替代成本是兩個(gè)單位，另外兩個(gè)操作的替代成本是一個(gè)。

例如，取兩個(gè)字符串?s=“Bitcoin”和?t=“Altcoin”。要從 s 到 t，需要用字母“A”和“l(fā)”兩次替換字母“B”和“I”。因此，d(t, s) = 2 * 2 = 4。

Levenshtein 距離有很多用例，如垃圾郵件過濾、計(jì)算生物學(xué)、彈性搜索等等。

? 漢明距離

漢明距離等于兩個(gè)相同長(zhǎng)度的碼字不同的位數(shù)。在二進(jìn)制世界中，它等于兩個(gè)二進(jìn)制消息之間不同位的數(shù)量。

例如，可以使用以下方法計(jì)算兩條消息之間的漢明距離：

它看起來像分類數(shù)據(jù)上下文中的曼哈頓距離。

對(duì)于長(zhǎng)度為 2 位的消息，此公式表示分隔兩個(gè)給定二進(jìn)制消息的邊數(shù)。它最多可以等于二。

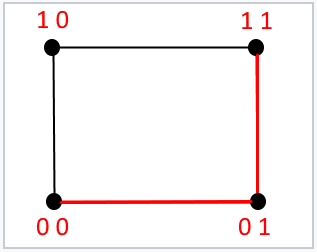
同樣，對(duì)于長(zhǎng)度為 3 位的消息，此公式表示分隔兩個(gè)給定二進(jìn)制消息的邊數(shù),它最多可以等于三。

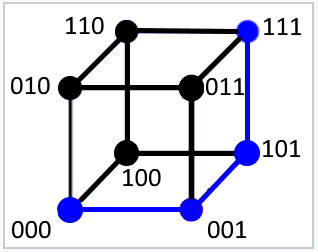
舉一些例子來說明漢明距離是如何計(jì)算的：

H(100001,?010001)?=?2
H(110,?111)?=?1

如果其中一個(gè)消息包含全零，則漢明距離稱為漢明權(quán)重，等于給定消息中非零數(shù)字的數(shù)量。在我們的例子中，它等于 1 的總數(shù)。

H(110111,000000)?=?W?(110111)?=?5

如果可能，漢明距離用于檢測(cè)和糾正通過不可靠的噪聲信道傳輸?shù)慕邮障⒅械腻e(cuò)誤。

? 杰卡德/谷本距離

用于衡量?jī)山M數(shù)據(jù)之間相似性的指標(biāo)。有人可能會(huì)爭(zhēng)辯說，為了衡量相似性，需要計(jì)算兩個(gè)給定集合之間的交集的大小（基數(shù)、元素?cái)?shù)）。

然而，僅憑公共元素的數(shù)量并不能告訴我們它與集合大小的相對(duì)關(guān)系。這就是 Jaccard 系數(shù)背后的直覺。

所以Jaccard提出，為了衡量相似度，你需要用交集的大小除以兩組數(shù)據(jù)的并集的大小。

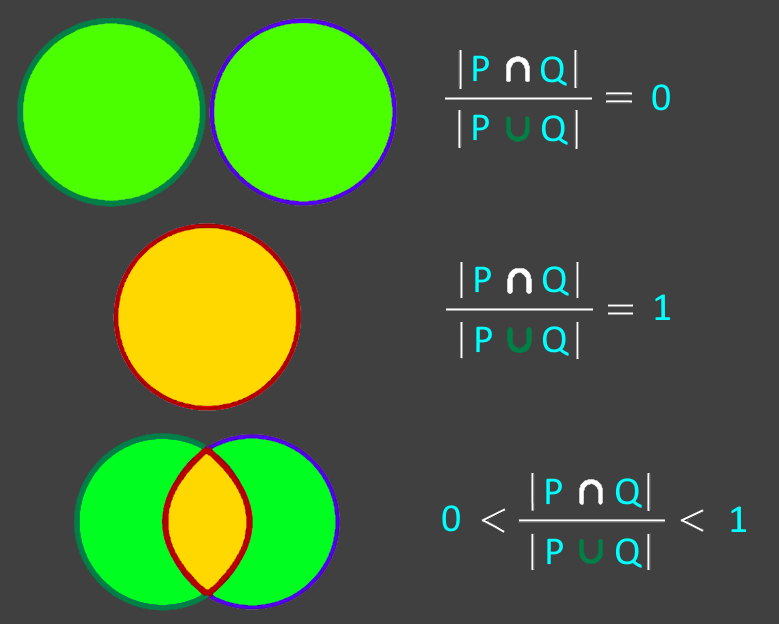
Jaccard 距離與 Jaccard 系數(shù)互補(bǔ)，用于衡量數(shù)據(jù)集之間的差異，計(jì)算公式為：

下圖說明了如何將此公式用于非二進(jìn)制數(shù)據(jù)的Jaccard 索引示例。

對(duì)于二元屬性，Jaccard 相似度使用以下公式計(jì)算：

Jaccard 索引可用于某些領(lǐng)域，如語義分割、文本挖掘、電子商務(wù)和推薦系統(tǒng)。

現(xiàn)在你可能會(huì)想：“好吧，但你剛才提到余弦距離也可以用于文本挖掘。你更喜歡使用什么作為給定聚類算法的度量？無論如何，這兩個(gè)指標(biāo)之間有什么區(qū)別？”

很高興你問了這個(gè)問題。為了回答這個(gè)問題，我們需要比較兩個(gè)公式的每一項(xiàng)。
Jaccard 和余弦公式

這兩個(gè)公式之間的唯一區(qū)別是分母項(xiàng)。不是用 Jaccard 計(jì)算兩個(gè)集合之間的聯(lián)合大小，而是計(jì)算 P 和 Q 之間點(diǎn)積的大小。而不是在 Jaccard 公式的分母中添加項(xiàng)；你正在計(jì)算余弦公式中兩者之間的乘積。我不知道那是什么解釋。據(jù)我所知，點(diǎn)積告訴我們一個(gè)向量在另一個(gè)方向上有多少。除此之外，如果有什么要補(bǔ)充的，可在評(píng)論區(qū)給我留言。

? S?rensen–Dice

S?rensen-Dice 距離是一種統(tǒng)計(jì)指標(biāo)，用于衡量數(shù)據(jù)集之間的相似性。它被定義為 P 和 Q 的交集大小的兩倍，除以每個(gè)數(shù)據(jù)集 P 和 Q 中元素的總和。

S?rensen–Dice 系數(shù)。

與 Jaccard 一樣，相似度值的范圍從零到一。但是，與 Jaccard 不同的是，這種相異性度量不是度量標(biāo)準(zhǔn)，因?yàn)樗粷M足三角不等式條件。

S?rensen–Dice 用于詞典編纂^[5]、圖像分割^[6]和其他應(yīng)用程序。

??Pydist2

pydist2是一個(gè)python包，1:1代碼采用pdist^[7]和pdist2^[8]?Matlab函數(shù)，用于計(jì)算觀測(cè)之間的距離。pydist2 當(dāng)前支持的測(cè)量距離的方法列表可在閱讀文檔中找到^[9]。

from?pydist2.distance?import?pdist1,?pdist2
import?numpy?as?np
x?=?np.array([[1,?2,?3],
???????[7,?8,?9],
???????[5,?6,?7],],?dtype=np.float32)
y?=?np.array([[10,?20,?30],
???????[70,?80,?90],
???????[50,?60,?70]],?dtype=np.float32)
a?=?pdist1(x)
a
>>>?array([10.39230485,??6.92820323,??3.46410162])
pdist1(x,?'seuclidean')
>>>?array([3.40168018,?2.26778677,?1.13389339])
pdist1(x,?'minkowski',?exp=3)
>>>?array([8.65349742,?5.76899828,?2.88449914])
pdist1(x,?'minkowski',?exp=2)
>>>?array([10.39230485,??6.92820323,??3.46410162])
pdist1(x,?'minkowski',?exp=1)
>>>?array([18.,?12.,??6.])
pdist1(x,?'cityblock')
>>>?array([18.,?12.,??6.])
pdist2(x,?y)
>>>?array([[?33.67491648,?135.69819453,?101.26203632],
...???????[?24.37211521,?125.35549449,??90.96153033],
...???????[?27.38612788,?128.80217389,??94.39279634]])
pdist2(x,?y,?'manhattan')
>>>?array([[?54.,?234.,?174.],
...???????[?36.,?216.,?156.],
...???????[?42.,?222.,?162.]])
pdist2(x,?y,?'sqeuclidean')
>>>?array([[?1134.,?18414.,?10254.],
...???????[??594.,?15714.,??8274.],
...???????[??750.,?16590.,??8910.]])
pdist2(x,?y,?'chi-squared')
>>>?array([[?22.09090909,?111.31927838,??81.41482329],
...???????[??8.48998061,??88.36363636,??59.6522841?],
...???????[?11.75121275,??95.51418525,??66.27272727]])
pdist2(x,?y,?'cosine')
>>>?array([[-5.60424152e-09,??4.05881305e-02,??3.16703408e-02],
...???????[?4.05880431e-02,??7.31070616e-08,??5.62480978e-04],
...???????[?3.16703143e-02,??5.62544701e-04,?-1.23279462e-08]])
pdist2(x,?y,?'earthmover')
>>>?array([[?90.,?450.,?330.],
...???????[?54.,?414.,?294.],
...???????[?66.,?426.,?306.]])

?? 寫在最后

這里已到達(dá)本文的結(jié)尾，本次內(nèi)容已經(jīng)分享結(jié)束了，在本文中，你了解了數(shù)據(jù)科學(xué)中使用的不同類型的指標(biāo)及其在許多領(lǐng)域的應(yīng)用。如果你有什么想說的，請(qǐng)盡管在文末留言區(qū)留言！

參考資料