深度學習多目標優(yōu)化的多個loss應該如何權(quán)衡

看了那么多篇理論慢慢的paper，終于找到一篇比較有工程意義的paper了。

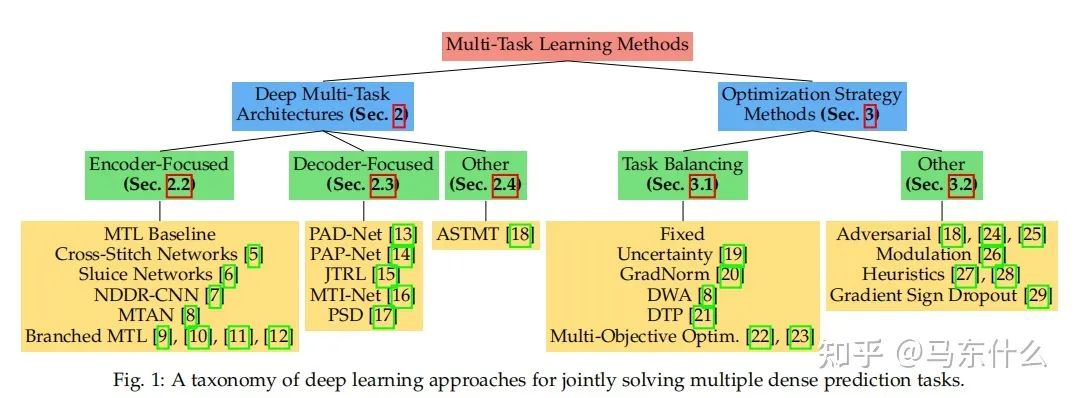
對于應用來說，這樣比較簡單直接的survey才是王道啊！感覺之前看的多任務的survey公式和定理太多，還是這樣的文章比較能夠幫助快速上手解決問題。

當然這里主要還是介紹optimization strategy部分。

這篇文章提到了多任務學習的兩個主要研究方向：

1、多任務學習的網(wǎng)絡結(jié)構(gòu)的構(gòu)造；

2、多任務學習對標的多目標優(yōu)化的方法；

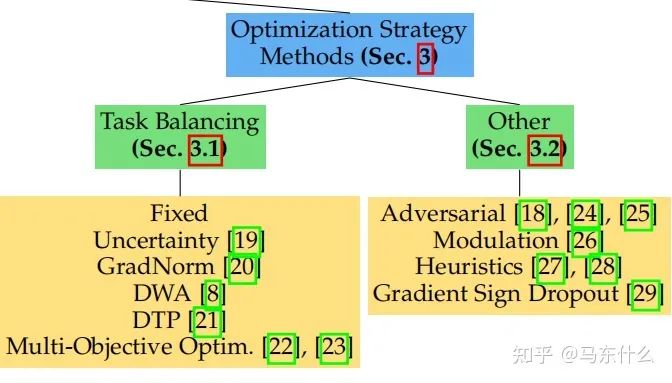
大體上分為兩種：

1、task balancing；

2、others。。。。

MTL中的一個重大挑戰(zhàn)源于優(yōu)化過程本身。特別是，我們需要仔細平衡所有任務的聯(lián)合訓練過程，以避免一個或多個任務在網(wǎng)絡權(quán)值中具有主導影響的情況。極端情況下，當某個任務的loss非常的大而其它任務的loss非常的小，此時多任務近似退化為單任務目標學習，網(wǎng)絡的權(quán)重幾乎完全按照大loss任務來進行更新，逐漸喪失了多任務學習的優(yōu)勢（具體優(yōu)勢可見：

馬東什么：多任務學習之非深度看起來頭大的部分

https://zhuanlan.zhihu.com/p/361464660

馬東什么：多任務學習之深度學習部分

https://zhuanlan.zhihu.com/p/361915151

第一大類方法 Task Balancing Approaches

假設(shè)任務特定權(quán)重的優(yōu)化目標wi和任務特定損失函數(shù)Li：

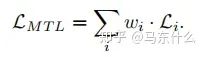
當使用隨機梯度下降來盡量減少上圖方程的總目標函數(shù)值（這是深度學習時代的標準方法），對共享層Wshare中的網(wǎng)絡權(quán)值通過以下規(guī)則進行更新：

從上圖的方程可以看出：

1、loss大則梯度更新量也大；

2、不同任務的loss差異大導致模型更新不平衡的本質(zhì)原因在于梯度大小；

3、通過調(diào)整不同任務的loss權(quán)重wi可以改善這個問題；

4、直接對不同任務的梯度進行處理也可以改善這個問題；

所以，后續(xù)的方法大體分為兩類：

1、在權(quán)重wi上做文章；

2、在梯度上做文章

在權(quán)重上做文章的方法：

1、Uncertainty Weighting

https://arxiv.org/pdf/1705.07115v3.pdf

人工定義多任務loss的權(quán)重是之前主要的使用方法，這種方法存在許多問題。模型性能對權(quán)重的選擇非常敏感，如圖所示。

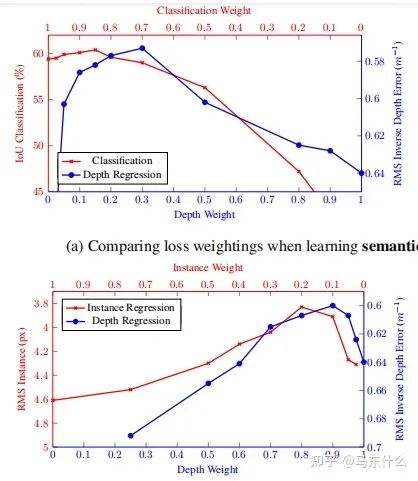
橫軸和縱軸分別是兩個任務的權(quán)重，曲線上的點對應不同權(quán)重下多任務深度學習網(wǎng)絡最終的訓練結(jié)果。

這些權(quán)重作為超參數(shù)調(diào)整起來非常的費事費力，每次測試通常需要很多的時間。

在貝葉斯學習

https://book.douban.com/subject/26284941/

關(guān)于python概率編程非常推薦這本書，這本也有中文版：

貝葉斯方法：概率編程與貝葉斯推斷

另外，tensorflow-probability在google上有關(guān)于這本書完整的代碼demo，非常淺顯易懂，上手快。

另外也有torch版的pyro

相關(guān)的代碼可見：

https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers

https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers

CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers

https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers

https://github.com/tensorflow/probability

https://github.com/pyro-ppl/pyro

中，認為模型存在兩種不確定性：

張子楊：【實驗筆記】深度學習中的兩種不確定性（上）

https://zhuanlan.zhihu.com/p/56986840

1.偶然不確定性
我們初高中學物理的時候，老師肯定提過偶然誤差這個詞。我們做小車下落測量重力加速度常數(shù)的時候，每次獲得的值都會有一個上下起伏。這是我們因為氣流擾動，測量精度不夠等原因所造成的，是無法被避免的一類誤差。在深度學習中，我們把這種誤差叫做偶然不確定性。
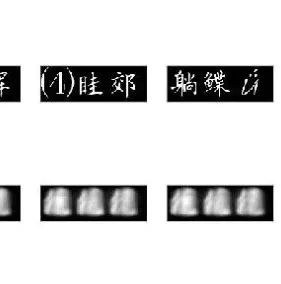
從深度學習的角度來舉例子，我們舉一個大家應該很比較熟悉的人臉關(guān)鍵點回歸問題[3]:

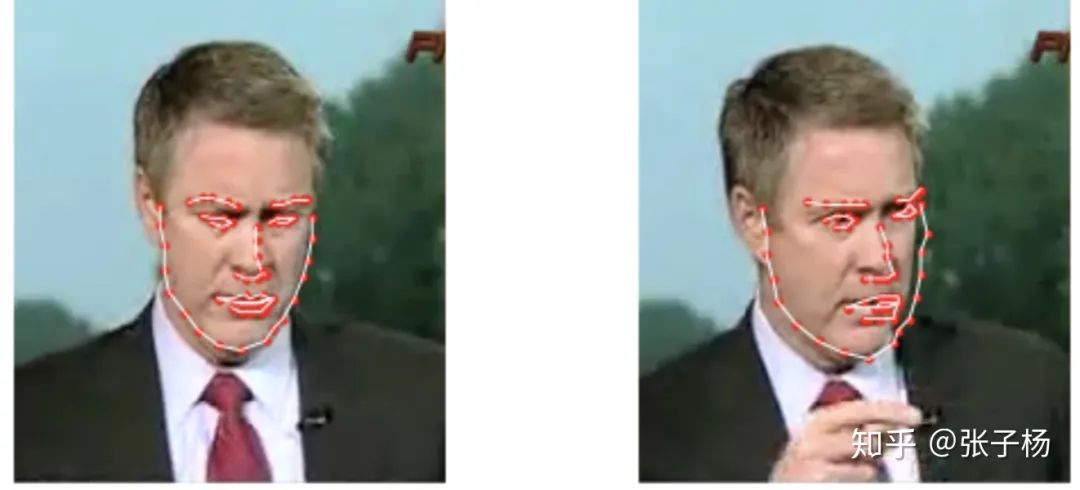
我們可以看到，對于很相似的一組數(shù)據(jù)，dataset的標注出現(xiàn)了比較大的誤差（見右圖的右側(cè)邊緣）。這樣的誤差并不是我們模型帶入的，而是數(shù)據(jù)本來就存在誤差。數(shù)據(jù)集里這樣的bias越大，我們的偶然不確定性就應該越大。

2.認知不確定性
認知不確定性是我們模型中存在的不確定性。就拿我們文章一開始舉的例子來說，假設(shè)我們訓練一個分類人臉和猩猩臉的模型，訓練中沒有做任何的增強，也就是說沒有做數(shù)據(jù)集的旋轉(zhuǎn)，模糊等操作。如果我給模型一個正常的人臉，或者是正常猩猩的臉，我們的模型應該對他所產(chǎn)生的結(jié)果的置信度很高。但是如果我給他貓的照片，一個模糊處理過得人臉，或者旋轉(zhuǎn)90°的猩猩臉，模型的置信度應該會特別低。換句話說，認知不確定性測量的，是我們的input data是否存在于已經(jīng)見過的數(shù)據(jù)的分布之中。

認知不確定性可以通過增加更多的data來緩解，偶然不確定性則需要對數(shù)據(jù)進行統(tǒng)一標準的處理。

偶然不確定性又存在兩種不確定性類別：

（補充：異方差和同方差，以經(jīng)典的線性回歸為例，我們常常假設(shè)線性回歸的誤差項滿足同方差，即誤差項的方差是相同的，如果不相同則為異方差，一個比較形象的例子：

什么是異方差？為什么異方差的出現(xiàn)通常與模型中某個解釋變量的變化有關(guān)？

https://www.zhihu.com/question/354637231/answer/895286217

1 數(shù)據(jù)依賴性（異方差不確定性）依賴于輸入數(shù)據(jù)，模型預測結(jié)果的殘差的方差即隨著數(shù)據(jù)的輸入發(fā)生變化；

2、任務依賴性（同方差不確定性）是不依賴于輸入數(shù)據(jù)的任意不確定性，它與模型輸出無關(guān)，是一個在所有輸入數(shù)據(jù)保持不變的情況下，在不同任務之間變化的量，因此，它可以被描述為與任務相關(guān)的不確定性，但是作者并沒有詳細解釋在多任務深度學習中的同方差不確定性的嚴格定義，而是認為同方差不確定性是由于任務相關(guān)的權(quán)重引起的。

下面我們定義fW(x)為nn的預測值，也就是我們熟悉的y_pred，

對于回歸型任務，我們定義下面的不確定性：

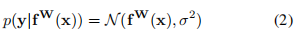
其中  在代碼中的體現(xiàn)，是一個可學習的參數(shù)，我們用這個參數(shù)服從的公式2的高斯分布作為同方差不確定性的衡量方法，即以 y_pred為均值向量，**2 作為方差的多元高斯分布；

對于分類問題有：

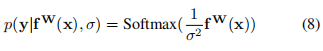
這被稱作是Boltzmann分布，也叫做吉布斯分布.

則在多目標的前提下，我們認為總的同方差不確定性可以用不同任務的不確定性的乘積來表示：

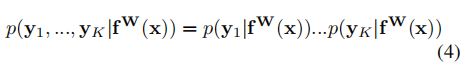
通過對公式（4）進行對數(shù)變換后可以得到：

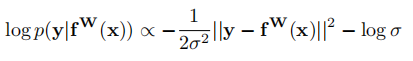
（這個正比的公式是怎么得到的。。。）

現(xiàn)在讓我們假設(shè)我們的模型輸出由兩個向量y1和y2組成，每個向量都遵循一個高斯分布：

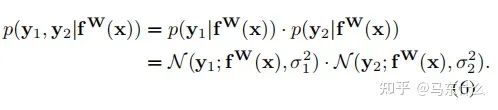
（這里作者沒有說清楚，實際上這里作者是假設(shè)我們有兩個回歸型的目標任務，并且損失函數(shù)使用的是mse）

然后得到多輸出模型的最小化目標函數(shù) L(W、σ1、σ2)：

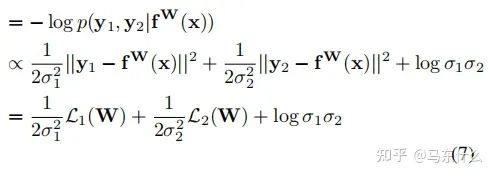
因此，對于公式（7），在新的回歸型任務中，我們可以將L1(W)和L2(W)用其它的回歸任務對應的損失函數(shù)來代替；

對于分類型任務，作者木有給出最終的化簡公式，不過對照下面的一個分類型任務+一個回歸型任務的化簡公式：

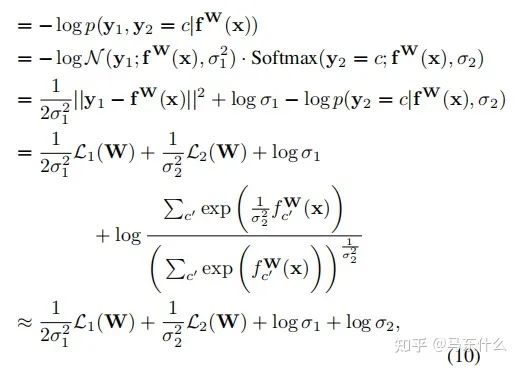
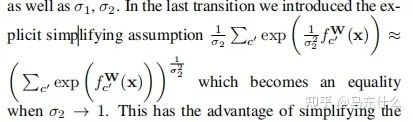
這里補充一下公式10的推導部分，具體的近似在上圖，將上圖帶入公式10即可。至于這個近似公式怎么來的，我也沒看明白。。。有懂得大佬求指正一下

我們可以先推出單個回歸型任務的不確定性度量公式，從而得到分類型任務的同方差不確定性的近似衡量公式為：

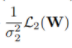
和

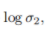
的和。

則也可以如法炮制，比較容易地寫出兩個分類型任務不確定性的化簡公式了，簡單來看就是分母少了2.（推導部分太頭大了就不看了）

這種構(gòu)造可以簡單地擴展到任意離散和連續(xù)損失函數(shù)的組合，允許我們以一種有原則和有充分根據(jù)的方式學習每一個損失的相對權(quán)重。這種損失是平滑可微的，并且分布形狀很好，使得任務權(quán)重不會收斂到零。相比之下，使用直接學習權(quán)值會導致快速收斂到零的權(quán)值。

總結(jié)一下，整體的思路就是用sigma來衡量同方差不確定性，同方差不確定性和任務有關(guān)，同方差不確定性越高的任務則意味著模任務相關(guān)的輸出的噪聲越多，任務越難以學習，因此在多任務模型訓練的過程中，其對應的sigma會增大，削弱這類任務的權(quán)重使得整體的多任務模型的訓練更加順暢和有效。

在代碼實現(xiàn)上有個小問題，也是比較常見的實現(xiàn)和論文存在區(qū)別的地方：

yaringal/multi-task-learning-example

https://github.com/yaringal/multi-task-learning-example/blob/master/multi-task-learning-example-pytorch.ipynb

這個是原論文作者的實現(xiàn)：基于兩個回歸型任務，損失函數(shù)mse為前提下得到的

def criterion(y_pred, y_true, log_vars):  loss = 0  for i in range(len(y_pred)):    precision = torch.exp(-log_vars[i])    diff = (y_pred[i]-y_true[i])**2. ## mse loss function    loss += torch.sum(precision * diff + log_vars[i], -1)  return torch.mean(loss)

原文提到了我們直接定義變量，這個變量是log(sigma的)(sigma表示的是方差，也就是下圖里面的那個二次項)，這樣可以避免loss公式中除0的問題：

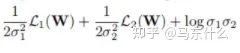
看了一下才發(fā)現(xiàn)這是萬惡的梯度下降法靈活的變量定義導致的，無論是torch還是tf中，變量為2x還是x都沒有區(qū)別，因為最終常數(shù)項都可以直接融合到變量的求解中，所以之前看的很多的paper的實現(xiàn)里，常數(shù)項都是直接包含在變量里省去不寫。。真是屑，，，

首先我們定義 log(sigma)=a(a是一個可學習的變量),則 torch.exp(-a)=torch.exp(-log(sigma))=torch.exp(log(sigma**-1))=1/sigma（這里0.5可以省去也可以包含進來，因為我們定義1/2*變量x和直接定義變量x，在梯度下降法求解的過程中沒有太大區(qū)別，然后是常數(shù)項的部分，作者在原文中提到，后面的常數(shù)項并不是很重要，放進來作為一種正則乘法太大的sigma（方差），這里后面的常數(shù)項，按照代碼的意思，是直接用了sigma方差來代替了標準差，其實差別也不大）

所以根據(jù)上述的設(shè)定對下面的代碼做了一些修改：

git上對應的代碼：

https://github.com/Mikoto10032/AutomaticWeightedLoss/blob/master/AutomaticWeightedLoss.py

找了幾個實現(xiàn)，發(fā)現(xiàn)代碼都有問題，只有這個git是完全忠于原文的，并且封裝的也比較舒服。

import torchimport torch.nn as nn
class AutomaticWeightedLoss(nn.Module):    """automatically weighted multi-task loss    Params：        num: int，the number of loss        x: multi-task loss    Examples：        loss1=1        loss2=2        awl = AutomaticWeightedLoss(2)        loss_sum = awl(loss1, loss2)    """    def __init__(self, num=2):        super(AutomaticWeightedLoss, self).__init__()        params = torch.ones(num, requires_grad=True)        self.params = torch.nn.Parameter(params) #parameters的封裝使得變量可以容易訪問到
    def forward(self, *x):        loss_sum = 0        for i, loss in enumerate(x):            loss_sum += 0.5 * torch.exp(-log_vars[i]) * loss + self.params[i]# +1避免了log 0的問題  log sigma部分對于整體loss的影響不大        return loss_sum

關(guān)于權(quán)重項部分

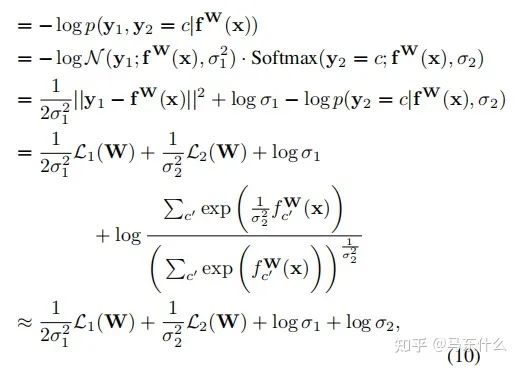
目前看過的三個git上都沒有對分類或者是回歸的loss區(qū)別對待，可以設(shè)置參數(shù)用于定義分類or回歸loss，從而給權(quán)重項部分的分布分別賦予回歸—2，分類—1。很多作者這部分沒有嚴格按照論文公式來預測，不過上面的code稍微改動一下就可以，但是其實也不用改。。常數(shù)項在梯度下降的過程中都會被優(yōu)化算法考慮進來的。

適配的話：

from torch import optimfrom AutomaticWeightedLoss import AutomaticWeightedLoss
model = Model()
awl = AutomaticWeightedLoss(2)  # we have 2 lossesloss_1 = ...loss_2 = ...
# learnable parametersoptimizer = optim.Adam([                {'params': model.parameters()},                {'params': awl.parameters(), 'weight_decay': 0}            ])
for i in range(epoch):    for data, label1, label2 in data_loader:        # forward        pred1, pred2 = Model(data)          # calculate losses        loss1 = loss_1(pred1, label1)        loss2 = loss_2(pred2, label2)        # weigh losses        loss_sum = awl(loss1, loss2)        # backward        optimizer.zero_grad()        loss_sum.backward()        optimizer.step()

這種方法的一個比較核心的問題也比較明顯吧：

1、同方差不確定性衡量的定義方式是否合理；

2、如果在多任務學習中，我們主要是希望主任務的效果好，輔助任務的效果可能不是很care，那么如果恰好主任務是同方差不確定性最高的，則使用這種方法可能會削弱主任務的效果，這是最大的問題，因為這種處理的方式針對的是整個多任務模型的總體loss來設(shè)計的，無法滿足對特定任務的不同程度的需求，因為作者原始的思路是不確定性越高的任務越應該削弱權(quán)重，但是反過來想，不確定性越高的任務越難，如果我們反而讓模型重點去學習這個任務，是否可以提高模型的能力；

3、 這里沒有考慮權(quán)重和為1的問題，不過我覺得作者本來也沒打算這么做，影響不大，權(quán)重之和是否為1并不是問題其實，本來多任務也不一定需要權(quán)重為1的設(shè)定，另外權(quán)重簡單做歸一化就可以得到權(quán)重為1了。。

4、實際應用的一個問題，權(quán)重可能會變成負數(shù)，導致我們最終的loss變成負數(shù)了。。。也就是部分任務對于最終總loss的貢獻是負貢獻，我認為可能是這部分任務的不確定性太大使得模型訓練困難，這個部分我們torch.relu進行截斷就可以了

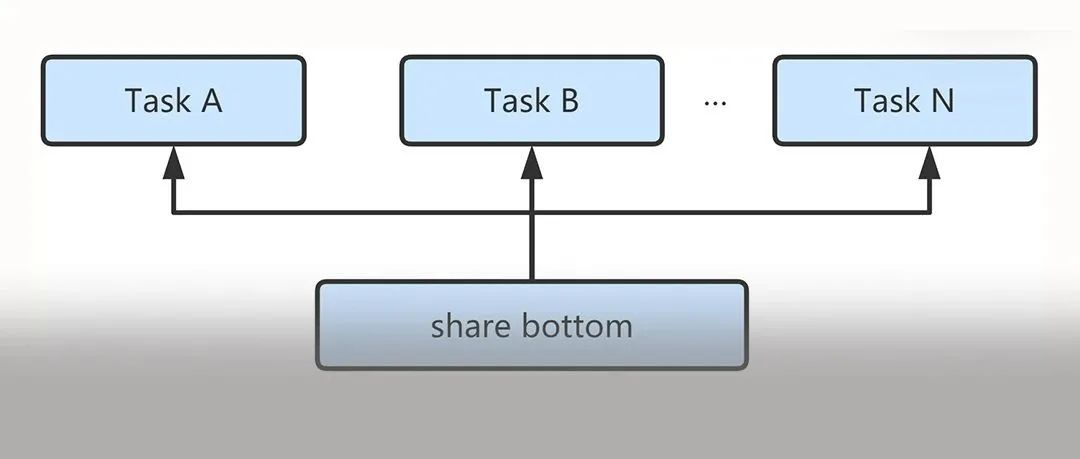
2、Grad Norm

梯度歸一化的主要目的在于希望不同任務任務對應的梯度具有相似的大小，從而控制多任務網(wǎng)絡的訓練。通過這樣做，我們鼓勵網(wǎng)絡以相同的速度學習所有的任務。grad norm本身不focus于不同任務之間的權(quán)重，而是將所有任務等同視之，只是希望所有任務的更新能夠相對接近從而避免了某個任務收斂了，某個任務還在收斂的路上的問題，這樣會導致：

1、模型訓練的效率低，最終運行時間由最復雜的任務決定；

2、復雜任務收斂的過程中，簡單任務的局部最優(yōu)權(quán)重可能會變差；