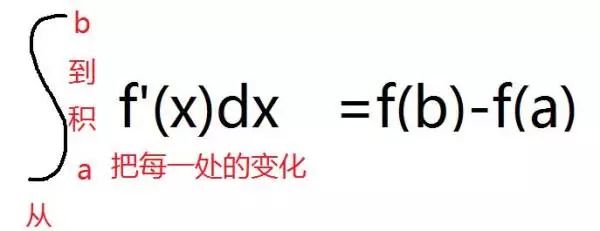大學(xué)數(shù)學(xué)(高數(shù)線代)直觀理解(一)
日期?:?2020年12月25日?? ? ??
正文共?:2275字
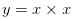 呢?這里有兩個(gè)x,每個(gè)x的變化的快慢都是由對(duì)方?jīng)Q定的,第一個(gè)x的變化快慢是x倍,第二個(gè)x的變化快慢是x倍,一共是?
呢?這里有兩個(gè)x,每個(gè)x的變化的快慢都是由對(duì)方?jīng)Q定的,第一個(gè)x的變化快慢是x倍,第二個(gè)x的變化快慢是x倍,一共是?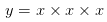 呢?這里有三個(gè)x,每個(gè)x的變化快慢都是,所以總變化快慢是?
呢?這里有三個(gè)x,每個(gè)x的變化快慢都是,所以總變化快慢是?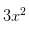
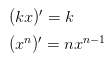
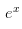 的變化率就是它自己,要理解的話得花大篇幅解釋e這個(gè)東西,在這里就不提了,反正記下來也挺簡單的。
的變化率就是它自己,要理解的話得花大篇幅解釋e這個(gè)東西,在這里就不提了,反正記下來也挺簡單的。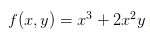 ,現(xiàn)在我問你,這個(gè)函數(shù)里,x的變化快慢被什么決定?
,現(xiàn)在我問你,這個(gè)函數(shù)里,x的變化快慢被什么決定?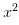 ,第二項(xiàng)里有兩個(gè)x,每個(gè)x的變化都是2xy,所以總變化是
,第二項(xiàng)里有兩個(gè)x,每個(gè)x的變化都是2xy,所以總變化是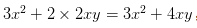 ,同樣的,我們其實(shí)也可以問,在這個(gè)函數(shù)里,y的變化快慢被什么決定?顯然是
,同樣的,我們其實(shí)也可以問,在這個(gè)函數(shù)里,y的變化快慢被什么決定?顯然是 。然后函數(shù)總的變化快慢是多少呢?
。然后函數(shù)總的變化快慢是多少呢?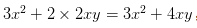
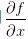 表示x的偏導(dǎo)數(shù)(變化率),
表示x的偏導(dǎo)數(shù)(變化率),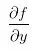 表示y的偏導(dǎo)數(shù)(變化率),在
表示y的偏導(dǎo)數(shù)(變化率),在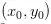 處的全微分公式寫做
處的全微分公式寫做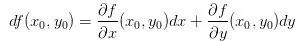 。就是說這個(gè)函數(shù)的增量等于x的增量加y的增量。好吧,一個(gè)知識(shí)點(diǎn)就這么完了,是不是有種感覺什么也沒說的感覺?沒錯(cuò)你相信我,真的就只是造出了幾個(gè)術(shù)語,搞出了幾個(gè)符號(hào),內(nèi)容就是我們說的那樣,那么的……廢話。其實(shí)我一直不喜歡這種寫法,但我沒有發(fā)明符號(hào)的閑心了,就姑且這么用,反正聽他們那些前輩說用多了還覺得挺美。
。就是說這個(gè)函數(shù)的增量等于x的增量加y的增量。好吧,一個(gè)知識(shí)點(diǎn)就這么完了,是不是有種感覺什么也沒說的感覺?沒錯(cuò)你相信我,真的就只是造出了幾個(gè)術(shù)語,搞出了幾個(gè)符號(hào),內(nèi)容就是我們說的那樣,那么的……廢話。其實(shí)我一直不喜歡這種寫法,但我沒有發(fā)明符號(hào)的閑心了,就姑且這么用,反正聽他們那些前輩說用多了還覺得挺美。
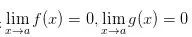 ,在點(diǎn)a的某去心鄰域內(nèi)兩者都可導(dǎo),且
,在點(diǎn)a的某去心鄰域內(nèi)兩者都可導(dǎo),且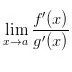 存在,那么有
存在,那么有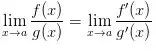 。
。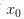 ,這一點(diǎn)的變化率是f'(x0),到x一共是變化了
,這一點(diǎn)的變化率是f'(x0),到x一共是變化了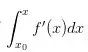 ,然而,f'(x)并不總是f'(x0),它是在變的,在處變化率是f(x0)'',這個(gè)變化率使得f(x0)'一共變化了
,然而,f'(x)并不總是f'(x0),它是在變的,在處變化率是f(x0)'',這個(gè)變化率使得f(x0)'一共變化了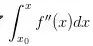 ,同樣,f(x0)''也是變化的,f(x0)''一共變化了
,同樣,f(x0)''也是變化的,f(x0)''一共變化了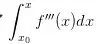 。總的來說會(huì)寫出這樣的式子:
。總的來說會(huì)寫出這樣的式子: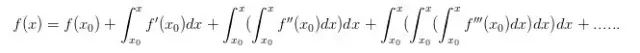
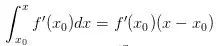 ,
,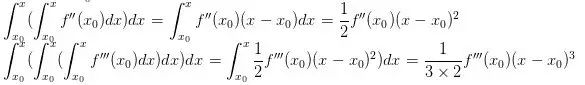
—?THE END —

評(píng)論
圖片
表情