歸并排序詳解（后序遍歷）

大家可能都對二叉樹的后序遍歷比較熟悉，實(shí)際上歸并排序本質(zhì)框架就是二叉樹的后序遍歷，根結(jié)點(diǎn)的遍歷只不過換成了治（Merge方法的調(diào)用），本文將結(jié)合動圖+代碼的方式進(jìn)行最通俗的講解。

「基本思想」：利用歸并的思想實(shí)現(xiàn)的排序方法，該算法采用經(jīng)典的分治（divide-and-conquer）策略（分治法將問題分(divide)成一些小的問題然后遞歸求解，而治(conquer)的階段則將分的階段得到的各答案修補(bǔ)在一起，即分而治之)。

分的過程

下面自制配了一張動圖來更好理解分的過程，其實(shí)完全就是左右根的后序遍歷，根的遍歷就是治（Merge方法的調(diào)用），分的過程中暫不可考慮根結(jié)點(diǎn)的遍歷，動圖中僅展示左邊的分的過程，以mid將其分組，遞歸的終止條件就是left==right，每組的right和left都不相同，左邊遞歸調(diào)用傳值left的值不變，right值為mid，右邊遞歸調(diào)用傳值left為mid+1，因?yàn)閙id是左邊的最后一個，所以要加1，右邊的值就是right。

代碼如下：

public?static?void?mergeSort(int[]?arr,?int?left,?int?right,?int[]?temp)?{
????if?(left?!=?right)?{//left和right的值會根據(jù)mid的值不斷變化
????????int?mid?=?(left?+?right)?/?2;
????????//向左遞歸進(jìn)行分解，動圖分組中靠左的部分
????????mergeSort(arr,?left,?mid,?temp);
????????//向右遞歸進(jìn)行分解??動圖分組中靠右的部分
????????mergeSort(arr,?mid?+?1,?right,?temp);
????????//合并(相當(dāng)于根)下面動圖中暫未表示合的思路
????????merge(arr,?left,?mid,?right,?temp);
????}
}

如下圖：「加上右邊邏輯上大致呈現(xiàn)二叉樹狀」

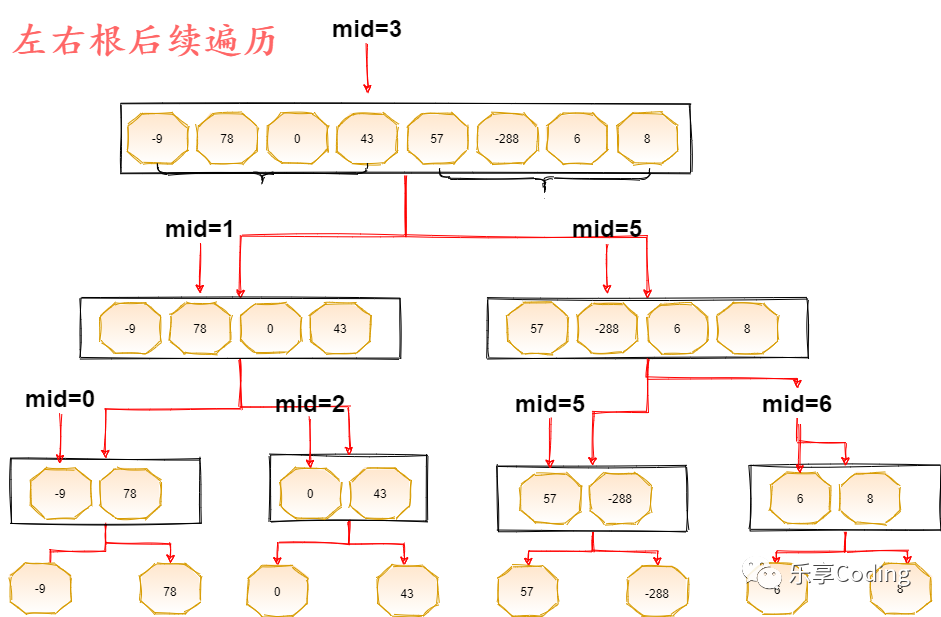
治---合的過程

根據(jù)二叉樹后序遍歷的特點(diǎn)，以本題為例，很明顯根節(jié)點(diǎn)需要遍歷7次，順序如下圖所示：

合并的規(guī)則如下：

定義一個與原數(shù)組長度相等的臨時空數(shù)組temp，初始索引t=0，之后每次合并（共7次）左結(jié)點(diǎn)的起始索引為left，末尾索引為mid，右節(jié)點(diǎn)的起始索引為mid+1，末尾索引為right，利用while循環(huán)將左結(jié)點(diǎn)的每一個值與右結(jié)點(diǎn)的每一個值做比較，判斷條件為（left <= mid && mid+1 <= right）,如果左結(jié)點(diǎn)的值小于右結(jié)點(diǎn)的值，則將左結(jié)點(diǎn)的值賦給temp[t]，之后t++，為保證不修改left的值所以將值賦給變量i，i++；相反如果右節(jié)點(diǎn)的值小于左結(jié)點(diǎn)的值，右結(jié)點(diǎn)的值賦給temp[t]，之后t++，為保證不修改mid+1的值所以將值賦給變量j，j++；這步做完后，發(fā)現(xiàn)左右個結(jié)點(diǎn)一定會有值剩下，因?yàn)樽笥医Y(jié)點(diǎn)的值總會有一個先到達(dá)判斷條件，++之后就終止了while循環(huán)，因此會剩余，這時又會出現(xiàn)兩種情況，一是左邊剩余（可能不止一個），另一個是右邊剩余（可能不止一個），因此還需要while循環(huán)，如果左邊剩余說明還沒到達(dá)mid（結(jié)尾索引），判斷條件為（i <= mid）,剩余元素一定是有序的并且是較大值，因此只需添加到臨時數(shù)組temp的末尾即可，右結(jié)點(diǎn)有值剩余只不過判斷條件變?yōu)椋╦ <= right），方法一樣。

最后每次合并都將temp的值copy到傳入的數(shù)組中去即可！

?public?static?void?merge(int[]?arr,?int?left,?int?mid,?int?right,?int[]?temp)?{
????????int?i?=?left;//左邊有序序列的初始索引
????????int?j?=?mid?+?1;//右邊有序序列的初始索引
????????int?t?=?0;?//指向temp數(shù)組的當(dāng)前索引

????????//一
????????//先把左右兩邊有序的數(shù)據(jù)按照規(guī)則填充到temp數(shù)組
????????//直到左右兩邊的有序序列，有一邊處理完畢為止
????????while?(i?<=?mid?&&?j?<=?right)?{?//繼續(xù)
????????????//如果左邊的有序序列的當(dāng)前元素小于等于右邊有序序列的當(dāng)前元素
????????????//即將左邊的當(dāng)前元素填充到temp數(shù)組
????????????//然后t++，i++
????????????if?(arr[i]?<=?arr[j])?{
????????????????temp[t]?=?arr[i];
????????????????t?+=?1;
????????????????i?+=?1;
????????????}?else?{?//反之，則將右邊的有序序列當(dāng)前元素填充到temp數(shù)組
????????????????temp[t]?=?arr[j];
????????????????t?+=?1;
????????????????j?+=?1;
????????????}
????????}
????????while?(i?<=?mid)?{//將左邊剩余元素全部填充進(jìn)temp中
????????????temp[t]?=?arr[i];
????????????t?+=?1;
????????????i?+=?1;
????????}
????????while?(j?<=?right)?{//將右序列剩余元素全部填充進(jìn)temp中
????????????temp[t]?=?arr[j];
????????????t?+=?1;
????????????j?+=?1;
????????}

????????//三
????????//將temp數(shù)組的元素拷貝到arr
????????//注意，并不是每次都拷貝所有
????????t?=?0;
????????int?tempLeft?=?left;
????????//第一次合并tempLeft=0，right=1??tempLeft=2，right=3??tempLeft=0，right=3
????????//最后一次tempLeft=0，right=1
????????while?(tempLeft?<=?right)?{
????????????arr[tempLeft]?=?temp[t];
????????????t?+=?1;
????????????tempLeft?+=?1;
????????}
????}

「由于合并次數(shù)過多，下圖僅將最后一次合并圖解在下圖」：

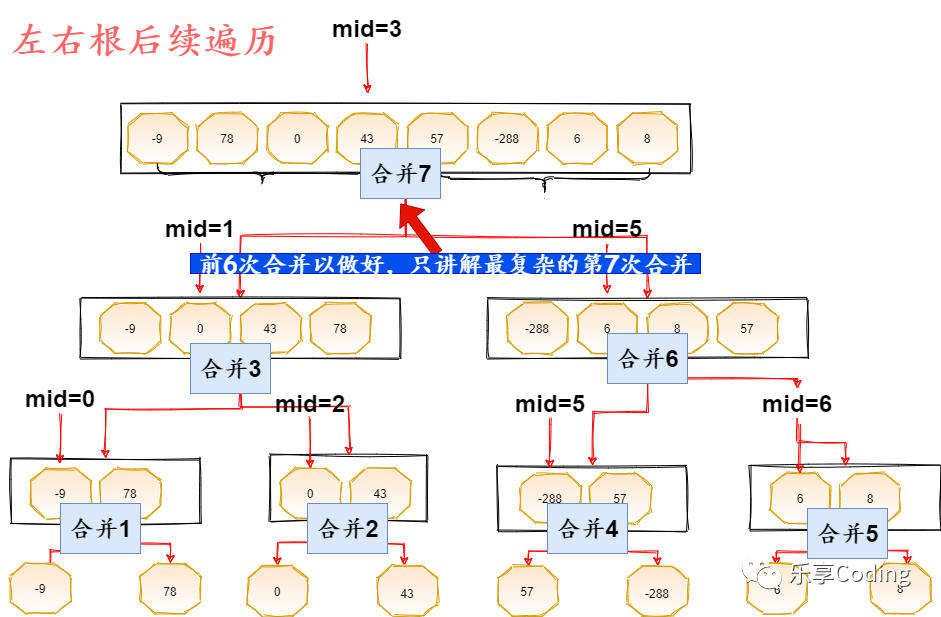
「第七次合并動圖圖解：」

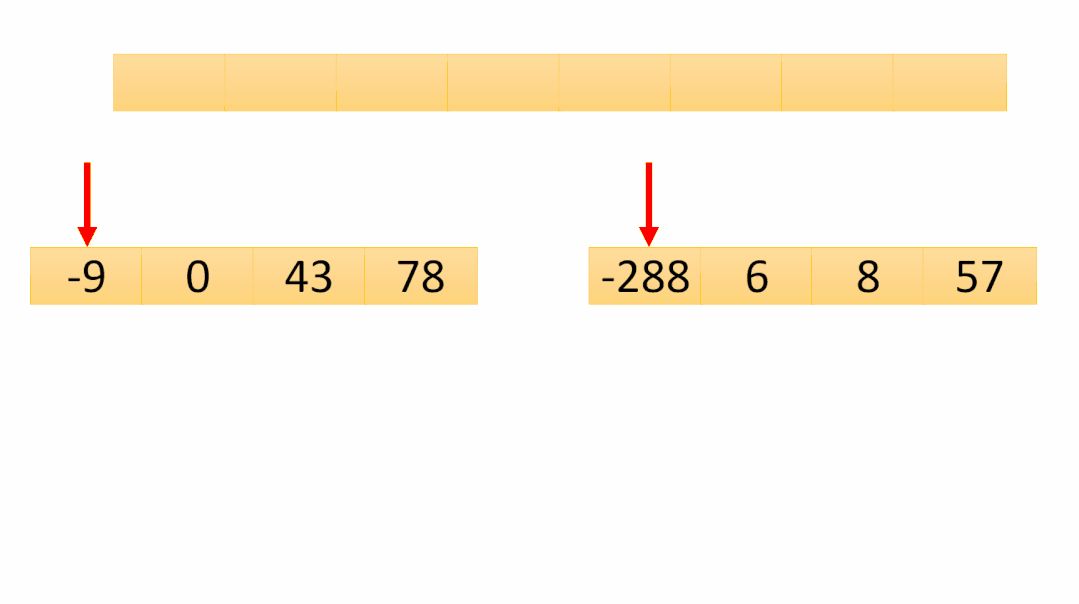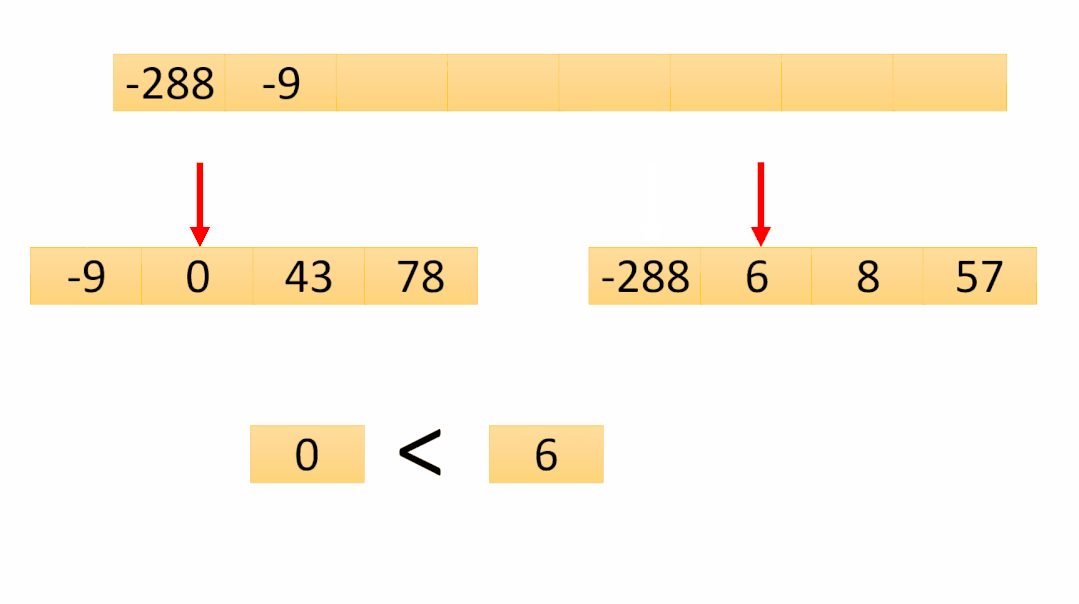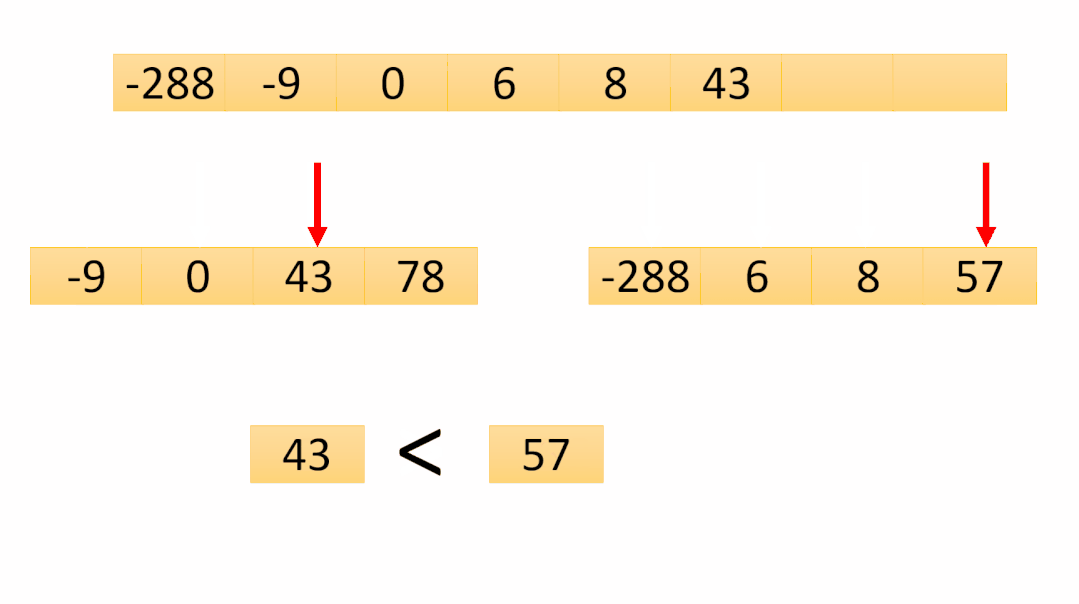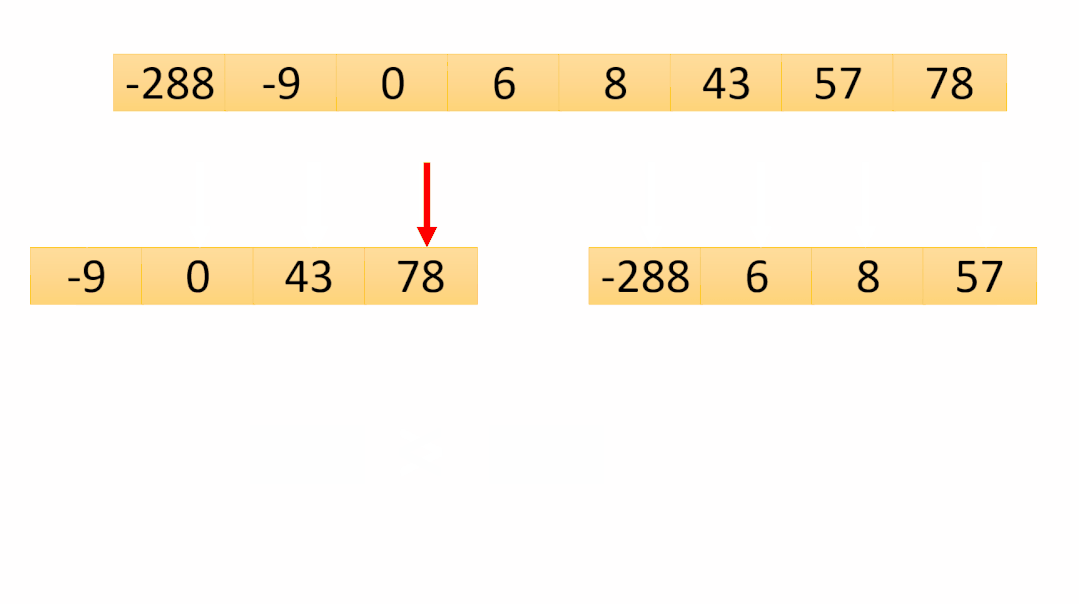
第七次合并是最后一次合并，可以看到數(shù)組已經(jīng)有序了，最后將temp數(shù)組copy到原數(shù)組即可排序完成！

時間復(fù)雜度：O(nlogn)

空間復(fù)雜度：O(n+logn)

由于歸并排序在歸并過程中需要與原始記錄序列同樣數(shù)量的存儲空間存放歸并結(jié)果以及遞歸深度為log2n的棧空間，因此空間復(fù)雜度為O(n+logn)，會造成空間的浪費(fèi)，因此可采用迭代繼續(xù)優(yōu)化，但是思路比較復(fù)雜，在本篇文章不做講解！