數(shù)字被修改了嗎？
日期?：?2021年10月05日?? ? ??
正文共?：2801字
從7.23動車事故開始，死亡35人便成為了一部分網(wǎng)民經(jīng)久不衰的話題。他們認為，當事故死亡人數(shù)超過35人時，省市官員就必須為此負責，因此官員將有動機將死亡人數(shù)實際超過35人的事故壓低到死亡35人以內(nèi)。那么，我們?nèi)绾闻袛噙@種現(xiàn)象是否存在？數(shù)字到底有沒有被修改？
由于隨機數(shù)字的出現(xiàn)會滿足一系列規(guī)律，因此，當一系列數(shù)字實際出現(xiàn)的規(guī)律與其應當出現(xiàn)的規(guī)律有顯著不同時，這一系列數(shù)字就可能被人為更改了。先看幾個簡單的例子：
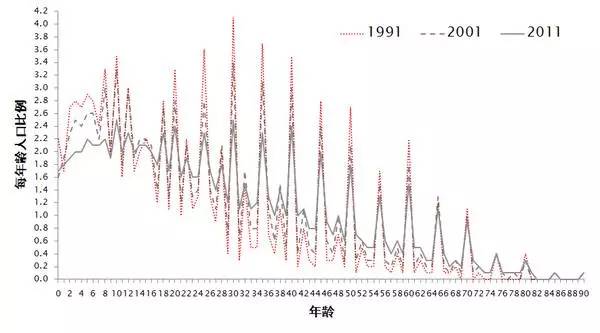
一，大量產(chǎn)生的隨機數(shù)字匯總后往往會具有平滑的性質(zhì)，印度人口普查的年齡是一個很好的反例。一般來說，如果沒有很強烈的年份偏好或者戰(zhàn)爭和饑荒，那么一個國家的分年齡人口應當是平滑的。在一個較小的區(qū)間內(nèi)，我們不應當看到波動很大的年齡結(jié)構(gòu)。因此，印度人口普查顯示的圖形，就顯得非常不正常——2011年，約有50%的人口錯報了自己的年齡，他們以尾數(shù)為0或者5的數(shù)字來替代自己的真實年齡。
二，隨機序列也有可能看起來不太隨機。將一個硬幣扔100次，得到一個序列，h為正面t為反面，下面哪個序列是真實的拋硬幣結(jié)果，哪個是腦補出來的？
序列1：
tthhhhhtthhhhtthhthhhtthhhhttththhhtthhhhhhtthhhhh
htthhthhhthhhhthhththtttththtthhtthhhhhttthhththtt
序列2：
hthtthhtthtthhhthtthtttththhthhththhhhthhtthtththh
hthhhthtththhhthttththhthhhthththhhhthhthttththhth
答案是序列1。在一個完全隨機的拋硬幣過程中，100次拋擲得到至少一個連續(xù)6次相同結(jié)果的序列的概率大于80%，得到至少一個連續(xù)5次相同結(jié)果的序列的概率大于90%。而在序列2里，最長的一串連續(xù)序列的長度僅有4。一列偽造的硬幣隨機數(shù)為了讓自己看起來更隨機，可能會頻繁變化正反，但正是這一點反而出賣了它的偽隨機本質(zhì)。
三，真實的數(shù)字序列會滿足Benford法則。在真實產(chǎn)生的十進制數(shù)字中，不同數(shù)碼的出現(xiàn)次數(shù)會滿足Benford法則，見下表：
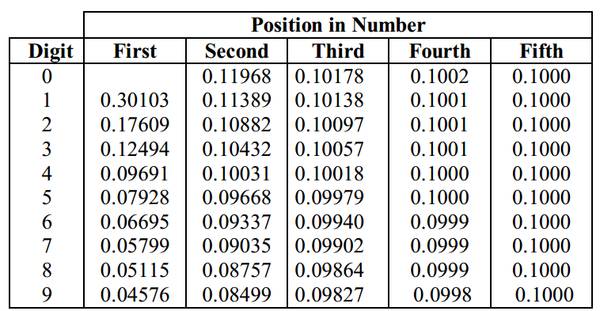上表的第一列表示隨機數(shù)字的第一位數(shù)中各數(shù)碼可能出現(xiàn)的概率，即首位數(shù)為1的概率為30.1%，首位數(shù)為2的概率為17.6%……首位數(shù)字為9的概率僅有4.6%。同樣我們也能計算第二位數(shù)字的出現(xiàn)概率。當一系列數(shù)字大幅度偏離Benford法則時，他就很有可能經(jīng)過人為調(diào)整。
ANZ銀行的研究人員就用該法則對中國的GDP增長數(shù)據(jù)進行了研究，他們發(fā)現(xiàn)，中國從1952年開始的年度GDP增長率中，首位數(shù)為1的次數(shù)為24次，高于Benford法則預測的18次；從1991年開始的季度GDP增長率中，第二位數(shù)為0的比例高達21次，而預測值僅有10次。該研究人員認為，這樣的偏差說明了中國的GDP數(shù)據(jù)可能存在相當?shù)摹高M位」現(xiàn)象，即將較大的數(shù)碼進位到10，才導致了第一位數(shù)的數(shù)碼1出現(xiàn)次數(shù)偏高且第二位數(shù)的數(shù)碼0的出現(xiàn)次數(shù)偏高。
在這份報告里，首位數(shù)的Benford法則討論其實是值得商榷的，假設(shè)一列隨機數(shù)以正態(tài)分布取自均值為10的區(qū)間內(nèi)，那么其首位數(shù)為1的概率將會高達50%，但這并不能說明這列隨機數(shù)字是人為調(diào)整過的。但第二位數(shù)字就不會出現(xiàn)首位數(shù)字碰到的問題，其分布則較為均勻，可以進行比較好的比較。
我們可以將中國和美國的季度GDP增長率的第二位數(shù)字的出現(xiàn)概率放在一起進行比較，得到下圖：
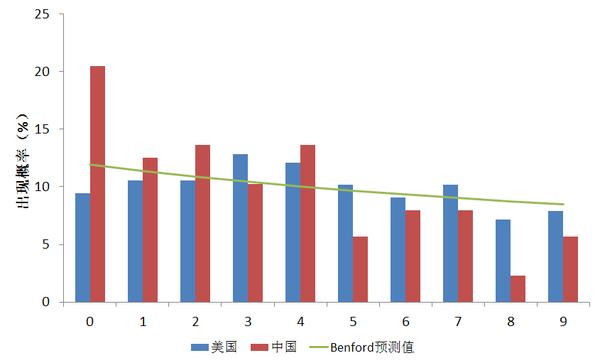可以看到，中國在第二位數(shù)等于0的概率確實要遠大于預測值12%，較大數(shù)碼的出現(xiàn)概率則要小于Benford法則預測值。美國的第二位數(shù)字與Benford法也有差距，體現(xiàn)在數(shù)碼0到3的出現(xiàn)概率提高上。但總體上來說，美國的統(tǒng)計數(shù)字距離Benford法則預測的差距要比中國統(tǒng)計數(shù)字的差距要小許多，中國在0和8兩個數(shù)字上的實際出現(xiàn)次數(shù)甚至可以在5%水平上顯著異于Benford法則的預測。中國是否將一系列尾數(shù)為8的GDP增長率給進位到10了？仍然不能確定，但至少這種解釋與數(shù)據(jù)所體現(xiàn)的現(xiàn)象不矛盾。
四，特大事故的死亡人數(shù)被修改了嗎？
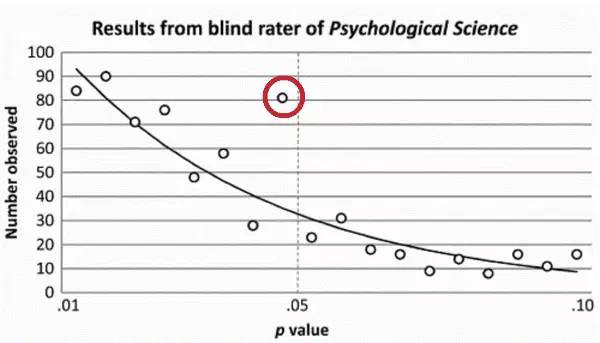
終于回到本文正題。先看一個研究數(shù)據(jù)是否調(diào)整的典型例子：p=0.05現(xiàn)象。在統(tǒng)計分析中，當一項檢驗的p值小于0.05時，這個結(jié)果一般被認為是在統(tǒng)計上顯著的。由于不顯著的結(jié)果難以發(fā)表，因此「調(diào)整」p值直到小于0.05，成了一些科研人員的最后手段。這一項研究（http://www.ncbi.nlm.nih.gov/pubmed/22853650）檢查了三份心理學期刊，發(fā)現(xiàn)報告的p值略微小于0.05的文章比例畸高于正常情況，顯示了「調(diào)整」p值可能已經(jīng)成為了一種客觀存在的現(xiàn)象。
在 事故查詢 里我們能夠查詢到中國從2000年至今的兩萬四千余起事故。在所有能查詢到的事故中（包括安全生產(chǎn)事故、交通事故與火災），從2000年7月至2014年底，死亡人數(shù)在10人以上的事故有1187起，按照死亡人數(shù)排序可得下圖：
將死亡在20到40人放大看，可得下圖：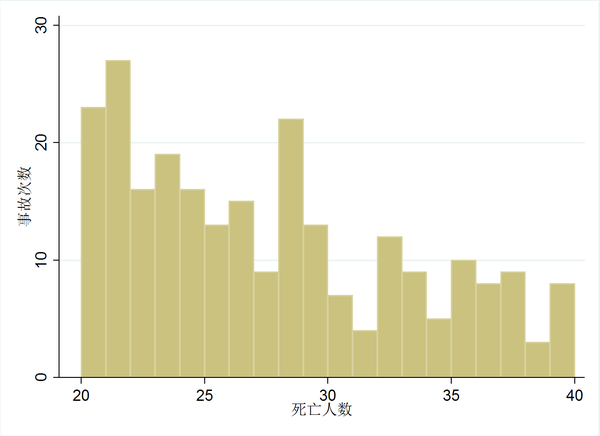
如果35人真的是一個分界點且在這個分界點附近的死亡瞞報現(xiàn)象真的存在，那么我們應當能看到報告死亡人數(shù)在33、34人的事故次數(shù)畸高（死亡35人及以上但被人為調(diào)整至35人以下，且不能調(diào)整幅度太大），而報告死亡35人的事故次數(shù)迅速下降。但是在圖中我們并不能看到這一現(xiàn)象。35人死亡的事故次數(shù)甚至還高于33和34人的次數(shù)。因此，35人這個事故死亡人數(shù)分界點，是不存在的。
不過，雖然在35這個值上不存在分界點，在其他值上就不一定了。按照p值研究的方法，我們可以畫一張類似的圖：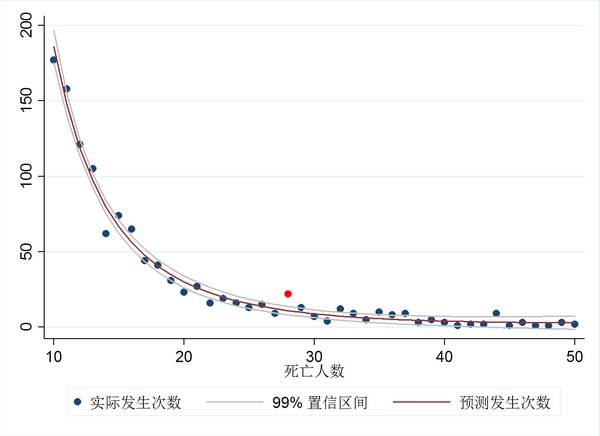
上圖中的橫軸為死亡人數(shù)，縱軸為事故次數(shù)，99%置信區(qū)間的擬合線公式為“預測次數(shù)=252746*死亡人數(shù)^(-3.037)”，是一個典型的冪律分布。可以看到，唯一一個實際事故次數(shù)大幅超過了預測事故次數(shù)99%置信區(qū)間上限死亡人數(shù)發(fā)生在28人。大幅度越過99%而非95%這個置信區(qū)間，可以說是非常少見的現(xiàn)象，這意味著在該模型成立的情況下此情形出現(xiàn)的概率遠小于1%。仔細檢查數(shù)據(jù)的話，死亡28人的事故有22次（模型預測10.2次），29人事故13次（模型預測9.1次），30人和31人迅速下降到7次和4次。
接下來，我們將所有事故里的交通事故專門拿出來做一張類似的圖。交通事故和生產(chǎn)安全事故尤其是煤礦的安全事故不同，后者的死亡發(fā)生在作業(yè)井下，因此統(tǒng)計人數(shù)往往不如前者那么容易被觀察到。相比于安全事故，交通事故的死亡數(shù)字修改會更加困難。
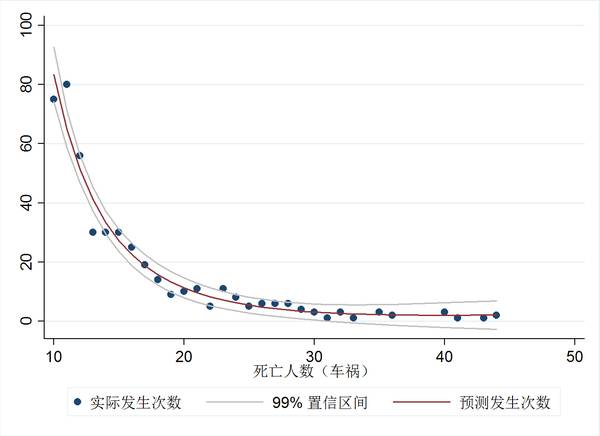上圖顯示，如果只把車禍拿出來，那么28、29人死亡事故的發(fā)生次數(shù)就顯著下降了，幾乎所有點落在了99%置信區(qū)間內(nèi)。換句話說，28人死亡事故的高頻率，是由生產(chǎn)事故頻率上升導致的。對于死亡人數(shù)更不容易被修改的交通事故，28人死亡的事故頻率相對于其他死亡人數(shù)的事故頻率并沒有上升。
是什么導致了這種現(xiàn)象呢？
以下為無關(guān)引用，僅供參考。
國務院《生產(chǎn)安全事故報告和調(diào)查處理條例》(2007年6月1日施行)第三條規(guī)定：“根據(jù)生產(chǎn)安全事故造成的人員傷亡或者直接經(jīng)濟損失，事故一般分為以下等級：特別重大事故、重大事故、較大事故和一般事故。
特別重大事故，是指造成30人（包括30人）以上死亡。
—?THE END —
