多智能體強(qiáng)化學(xué)習(xí)入門(mén)(一)——基礎(chǔ)知識(shí)與博弈

作者:ECKai(強(qiáng)化學(xué)習(xí),多智能體強(qiáng)化學(xué)習(xí))
文章僅作為學(xué)術(shù)交流,著作權(quán)歸屬作者,侵刪
一、引言
在多智能體系統(tǒng)中,每個(gè)智能體通過(guò)與環(huán)境進(jìn)行交互獲取獎(jiǎng)勵(lì)值(reward)來(lái)學(xué)習(xí)改善自己的策略,從而獲得該環(huán)境下最優(yōu)策略的過(guò)程就多智能體強(qiáng)化學(xué)習(xí)。
在單智能體強(qiáng)化學(xué)習(xí)中,智能體所在的環(huán)境是穩(wěn)定不變的,但是在多智能體強(qiáng)化學(xué)習(xí)中,環(huán)境是復(fù)雜的、動(dòng)態(tài)的,因此給學(xué)習(xí)過(guò)程帶來(lái)很大的困難。
維度爆炸:在單體強(qiáng)化學(xué)習(xí)中,需要存儲(chǔ)狀態(tài)值函數(shù)或動(dòng)作-狀態(tài)值函數(shù)。在多體強(qiáng)化學(xué)習(xí)中,狀態(tài)空間變大,聯(lián)結(jié)動(dòng)作空間(聯(lián)結(jié)動(dòng)作是指每個(gè)智能體當(dāng)前動(dòng)作組合而成的多智能體系統(tǒng)當(dāng)前時(shí)刻的動(dòng)作,聯(lián)結(jié)動(dòng)作
 ,
,  指第i個(gè)智能體在時(shí)刻t選取的動(dòng)作。)隨智能體數(shù)量指數(shù)增長(zhǎng),因此多智能體系統(tǒng)維度非常大,計(jì)算復(fù)雜。
指第i個(gè)智能體在時(shí)刻t選取的動(dòng)作。)隨智能體數(shù)量指數(shù)增長(zhǎng),因此多智能體系統(tǒng)維度非常大,計(jì)算復(fù)雜。目標(biāo)獎(jiǎng)勵(lì)確定困難:多智能體系統(tǒng)中每個(gè)智能體的任務(wù)可能不同,但是彼此之間又相互耦合影響。獎(jiǎng)勵(lì)設(shè)計(jì)的優(yōu)劣直接影響學(xué)習(xí)到的策略的好壞。
不穩(wěn)定性:在多智能體系統(tǒng)中,多個(gè)智能體是同時(shí)學(xué)習(xí)的。當(dāng)同伴的策略改變時(shí),每個(gè)智能體自身的最優(yōu)策略也可能會(huì)變化,這將對(duì)算法的收斂性帶來(lái)影響。
探索-利用:探索不光要考慮自身對(duì)環(huán)境的探索,也要對(duì)同伴的策略變化進(jìn)行探索,可能打破同伴策略的平衡狀態(tài)。每個(gè)智能體的探索都可能對(duì)同伴智能體的策略產(chǎn)生影響,這將使算法很難穩(wěn)定,學(xué)習(xí)速度慢。
在多智能體系統(tǒng)中智能體之間可能涉及到合作與競(jìng)爭(zhēng)等關(guān)系,引入博弈的概念,將博弈論與強(qiáng)化學(xué)習(xí)相結(jié)合可以很好的處理這些問(wèn)題。
二、博弈論基礎(chǔ)
在本節(jié)中主要介紹多智能體強(qiáng)化學(xué)習(xí)中需要用到的一些概念及定義,僅局限于多智能體強(qiáng)化學(xué)習(xí)算法的理解分析。包括矩陣博弈、靜態(tài)博弈、階段博弈、重復(fù)博弈和隨機(jī)博弈等概念。
1. 矩陣博弈
一個(gè)矩陣博弈可以表示為  ,n表示智能體數(shù)量,
,n表示智能體數(shù)量,  是第i個(gè)智能體的動(dòng)作集,
是第i個(gè)智能體的動(dòng)作集,  表示第i個(gè)智能體的獎(jiǎng)勵(lì)函數(shù),從獎(jiǎng)勵(lì)函數(shù)可以看出每個(gè)智能體獲得的獎(jiǎng)勵(lì)與多智能體系統(tǒng)的聯(lián)結(jié)動(dòng)作有關(guān),聯(lián)結(jié)動(dòng)作空間為
表示第i個(gè)智能體的獎(jiǎng)勵(lì)函數(shù),從獎(jiǎng)勵(lì)函數(shù)可以看出每個(gè)智能體獲得的獎(jiǎng)勵(lì)與多智能體系統(tǒng)的聯(lián)結(jié)動(dòng)作有關(guān),聯(lián)結(jié)動(dòng)作空間為  。每個(gè)智能體的策略是一個(gè)關(guān)于其動(dòng)作空間的概率分布,每個(gè)智能體的目標(biāo)是最大化其獲得的獎(jiǎng)勵(lì)值。
。每個(gè)智能體的策略是一個(gè)關(guān)于其動(dòng)作空間的概率分布,每個(gè)智能體的目標(biāo)是最大化其獲得的獎(jiǎng)勵(lì)值。
令  表示智能體i在,聯(lián)結(jié)策略
表示智能體i在,聯(lián)結(jié)策略  下的期望獎(jiǎng)勵(lì),即值函數(shù)。
下的期望獎(jiǎng)勵(lì),即值函數(shù)。
定義1:納什均衡
在矩陣博弈中,如果聯(lián)結(jié)策略  滿足
滿足

則為一個(gè)納什均衡。
總體來(lái)說(shuō),納什均衡就是一個(gè)所有智能體的聯(lián)結(jié)策略。在納什均衡處,對(duì)于所有智能體而言都不能在僅改變自身策略的情況下,來(lái)獲得更大的獎(jiǎng)勵(lì)。
定義  表示在執(zhí)行聯(lián)結(jié)動(dòng)作
表示在執(zhí)行聯(lián)結(jié)動(dòng)作  時(shí),智能體i所能獲得的期望獎(jiǎng)勵(lì)。令
時(shí),智能體i所能獲得的期望獎(jiǎng)勵(lì)。令  表示第i個(gè)智能體選取動(dòng)作
表示第i個(gè)智能體選取動(dòng)作  的概率。則納什均衡的另一種定義方式如下
的概率。則納什均衡的另一種定義方式如下 
定義2:嚴(yán)格納什均衡
若(1)式嚴(yán)格大于,則  為嚴(yán)格納什均衡。
為嚴(yán)格納什均衡。
定義3:完全混合策略
若一個(gè)策略對(duì)于智能體動(dòng)作集中的所有動(dòng)作的概率都大于0,則這個(gè)策略為一個(gè)完全混合策略。
定義4:純策略
若智能體的策略對(duì)一個(gè)動(dòng)作的概率分布為1,對(duì)其余的動(dòng)作的概率分布為0,則這個(gè)策略為一個(gè)純策略。
2. 兩個(gè)智能體的矩陣博弈中的納什均衡
本節(jié)介紹針對(duì)一個(gè)兩智能體博弈問(wèn)題的常規(guī)建模方式,并介紹幾種常見(jiàn)的博弈形式。后面的很多多智能體強(qiáng)化學(xué)習(xí)算法都是以此為基礎(chǔ)建立起來(lái)的,雙智能體矩陣博弈對(duì)于多智能體強(qiáng)化學(xué)習(xí)類(lèi)似于感知機(jī)對(duì)于神經(jīng)網(wǎng)絡(luò)。
在雙智能體矩陣博弈中,我們可以設(shè)計(jì)一個(gè)矩陣,矩陣每一個(gè)元素的索引坐標(biāo)表示一個(gè)聯(lián)結(jié)動(dòng)作  ,第i個(gè)智能體的獎(jiǎng)勵(lì)矩陣
,第i個(gè)智能體的獎(jiǎng)勵(lì)矩陣  的元素
的元素  就表示第一個(gè)智能體采用動(dòng)作x,第二個(gè)智能體采用動(dòng)作y時(shí)第i個(gè)智能體獲得的獎(jiǎng)勵(lì)。通常我們將第一個(gè)智能體定義為行智能體,第二個(gè)智能體定義為列智能體,行號(hào)表示第一個(gè)智能體選取的動(dòng)作,列號(hào)表示第二個(gè)智能體選取的動(dòng)作。則對(duì)于只有2個(gè)動(dòng)作的智能體,其獎(jiǎng)勵(lì)矩陣分別可以寫(xiě)為
就表示第一個(gè)智能體采用動(dòng)作x,第二個(gè)智能體采用動(dòng)作y時(shí)第i個(gè)智能體獲得的獎(jiǎng)勵(lì)。通常我們將第一個(gè)智能體定義為行智能體,第二個(gè)智能體定義為列智能體,行號(hào)表示第一個(gè)智能體選取的動(dòng)作,列號(hào)表示第二個(gè)智能體選取的動(dòng)作。則對(duì)于只有2個(gè)動(dòng)作的智能體,其獎(jiǎng)勵(lì)矩陣分別可以寫(xiě)為

定義5. 零和博弈
零和博弈中,兩個(gè)智能體是完全競(jìng)爭(zhēng)對(duì)抗關(guān)系,則  。在零和博弈中只有一個(gè)納什均衡值,即使可能有很多納什均衡策略,但是期望的獎(jiǎng)勵(lì)是相同的。
。在零和博弈中只有一個(gè)納什均衡值,即使可能有很多納什均衡策略,但是期望的獎(jiǎng)勵(lì)是相同的。
定義6. 一般和博弈
一般和博弈是指任何類(lèi)型的矩陣博弈,包括完全對(duì)抗博弈、完全合作博弈以及二者的混合博弈。在一般和博弈中可能存在多個(gè)納什均衡點(diǎn)。
我們定義策略  為智能體i的動(dòng)作集中每個(gè)動(dòng)作的概率集合,
為智能體i的動(dòng)作集中每個(gè)動(dòng)作的概率集合,  表示可選的動(dòng)作數(shù)量,則值函數(shù)
表示可選的動(dòng)作數(shù)量,則值函數(shù)  可以表示為
可以表示為

納什均衡策略  可以表示為
可以表示為

 表示第
表示第  個(gè)智能體的策略空間,
個(gè)智能體的策略空間,  表示另一個(gè)智能體。
表示另一個(gè)智能體。
如上定義一個(gè)兩智能體一般和博弈為

若滿足

則$l,f$為純策略嚴(yán)格納什均衡,  表示除了
表示除了  的另一個(gè)策略。
的另一個(gè)策略。
3. 線性規(guī)劃求解雙智能體零和博弈
求解雙智能體零和博弈的公式如下

上式的意義為,每個(gè)智能體最大化在與對(duì)手博弈中最差情況下的期望獎(jiǎng)勵(lì)值。
將博弈寫(xiě)為如下形式

定義  表示第一個(gè)智能體選擇動(dòng)作
表示第一個(gè)智能體選擇動(dòng)作  的概率,
的概率,  表示第二個(gè)智能體選擇動(dòng)作
表示第二個(gè)智能體選擇動(dòng)作  的概率。則對(duì)于第一個(gè)智能體,可以列寫(xiě)如下線性規(guī)劃
的概率。則對(duì)于第一個(gè)智能體,可以列寫(xiě)如下線性規(guī)劃

同理,可以列出第二個(gè)智能體的納什策略的線性規(guī)劃

求解上式就可得到納什均衡策略。
4. 幾個(gè)博弈概念
馬爾可夫決策過(guò)程包含一個(gè)智能體與多個(gè)狀態(tài)。矩陣博弈包括多個(gè)智能體與一個(gè)狀態(tài)。隨機(jī)博弈(stochastic game / Markov game)是馬爾可夫決策過(guò)程與矩陣博弈的結(jié)合,具有多個(gè)智能體與多個(gè)狀態(tài),即多智能體強(qiáng)化學(xué)習(xí)。為更好地理解,引入如下定義
靜態(tài)博弈:static/stateless game是指沒(méi)有狀態(tài)s,不存在動(dòng)力學(xué)使?fàn)顟B(tài)能夠轉(zhuǎn)移的博弈。例如一個(gè)矩陣博弈。
階段博弈:stage game,是隨機(jī)博弈的組成成分,狀態(tài)s是固定的,相當(dāng)于一個(gè)狀態(tài)固定的靜態(tài)博弈,隨機(jī)博弈中的Q值函數(shù)就是該階段博弈的獎(jiǎng)勵(lì)函數(shù)。若干狀態(tài)的階段博弈組成一個(gè)隨機(jī)博弈。
重復(fù)博弈:智能體重復(fù)訪問(wèn)同一個(gè)狀態(tài)的階段博弈,并且在訪問(wèn)同一個(gè)狀態(tài)的階段博弈的過(guò)程中收集其他智能體的信息與獎(jiǎng)勵(lì)值,并學(xué)習(xí)更好的Q值函數(shù)與策略。
多智能體強(qiáng)化學(xué)習(xí)就是一個(gè)隨機(jī)博弈,將每一個(gè)狀態(tài)的階段博弈的納什策略組合起來(lái)成為一個(gè)智能體在動(dòng)態(tài)環(huán)境中的策略。并不斷與環(huán)境交互來(lái)更新每一個(gè)狀態(tài)的階段博弈中的Q值函數(shù)(博弈獎(jiǎng)勵(lì))。
對(duì)于一個(gè)隨機(jī)博弈可以寫(xiě)為  ,其中n表示智能體數(shù)量,S表示狀態(tài)空間,
,其中n表示智能體數(shù)量,S表示狀態(tài)空間,  表示第i個(gè)智能體的動(dòng)作空間,
表示第i個(gè)智能體的動(dòng)作空間,  表示狀態(tài)轉(zhuǎn)移概率,
表示狀態(tài)轉(zhuǎn)移概率,  表示第i個(gè)智能體在當(dāng)前狀態(tài)與聯(lián)結(jié)動(dòng)作下獲得的回報(bào)值,
表示第i個(gè)智能體在當(dāng)前狀態(tài)與聯(lián)結(jié)動(dòng)作下獲得的回報(bào)值,  表示累積獎(jiǎng)勵(lì)折扣系數(shù)。隨機(jī)博弈也具有馬爾科夫性,下一個(gè)狀態(tài)與獎(jiǎng)勵(lì)只與當(dāng)前狀態(tài)與當(dāng)前的聯(lián)結(jié)動(dòng)作有關(guān)。
表示累積獎(jiǎng)勵(lì)折扣系數(shù)。隨機(jī)博弈也具有馬爾科夫性,下一個(gè)狀態(tài)與獎(jiǎng)勵(lì)只與當(dāng)前狀態(tài)與當(dāng)前的聯(lián)結(jié)動(dòng)作有關(guān)。
對(duì)于一個(gè)多智能體強(qiáng)化學(xué)習(xí)過(guò)程,就是找到每一個(gè)狀態(tài)的納什均衡策略,然后將這些策略聯(lián)合起來(lái)。  就是一個(gè)智能體i的策略,在每個(gè)狀態(tài)選出最優(yōu)的納什策略。多智能體強(qiáng)化學(xué)習(xí)最優(yōu)策略(隨機(jī)博弈的納什均衡策略)可以寫(xiě)為
就是一個(gè)智能體i的策略,在每個(gè)狀態(tài)選出最優(yōu)的納什策略。多智能體強(qiáng)化學(xué)習(xí)最優(yōu)策略(隨機(jī)博弈的納什均衡策略)可以寫(xiě)為  ,且
,且  滿足
滿足

 為
為  折扣累積狀態(tài)值函數(shù),用
折扣累積狀態(tài)值函數(shù),用  簡(jiǎn)記上式。用
簡(jiǎn)記上式。用  表示動(dòng)作狀態(tài)
表示動(dòng)作狀態(tài)  折扣累積值函數(shù),在每個(gè)固定狀態(tài)s的階段博弈中,就是利用
折扣累積值函數(shù),在每個(gè)固定狀態(tài)s的階段博弈中,就是利用  作為博弈的獎(jiǎng)勵(lì)求解納什均衡策略的。根據(jù)強(qiáng)化學(xué)習(xí)中的Bellman公式,可得
作為博弈的獎(jiǎng)勵(lì)求解納什均衡策略的。根據(jù)強(qiáng)化學(xué)習(xí)中的Bellman公式,可得

MARL(多智能體強(qiáng)化學(xué)習(xí))的納什策略可以改寫(xiě)為

根據(jù)每個(gè)智能體的獎(jiǎng)勵(lì)函數(shù)可以對(duì)隨機(jī)博弈進(jìn)行分類(lèi)。若智能體的獎(jiǎng)勵(lì)函數(shù)相同,則稱為完全合作博弈或團(tuán)隊(duì)博弈。若智能體的獎(jiǎng)勵(lì)函數(shù)逆號(hào),則稱為完全競(jìng)爭(zhēng)博弈或零和博弈。為了求解隨機(jī)博弈,需要求解每個(gè)狀態(tài)s的階段博弈,每個(gè)階段博弈的獎(jiǎng)勵(lì)值就是  。
。
三、隨機(jī)博弈示例
定義一個(gè)2*2的網(wǎng)格博弈,兩個(gè)智能體分別表示為  ,
,  ,1的初始位置在左下角,2的初始位置在右上角,每一個(gè)智能體都想以最快的方式達(dá)到G標(biāo)志的地方。從初始位置開(kāi)始,每個(gè)智能體都有兩個(gè)動(dòng)作可以選擇。只要有一個(gè)智能體達(dá)到G則游戲結(jié)束,達(dá)到G的智能體獲得獎(jiǎng)勵(lì)10,獎(jiǎng)勵(lì)折扣率為0.9。虛線表示欄桿,智能體穿過(guò)欄桿的概率為0.5。該隨機(jī)博弈一共包含7個(gè)狀態(tài)。這個(gè)博弈的納什均衡策略是,每個(gè)智能體到達(dá)鄰居位置而不穿過(guò)欄桿。
,1的初始位置在左下角,2的初始位置在右上角,每一個(gè)智能體都想以最快的方式達(dá)到G標(biāo)志的地方。從初始位置開(kāi)始,每個(gè)智能體都有兩個(gè)動(dòng)作可以選擇。只要有一個(gè)智能體達(dá)到G則游戲結(jié)束,達(dá)到G的智能體獲得獎(jiǎng)勵(lì)10,獎(jiǎng)勵(lì)折扣率為0.9。虛線表示欄桿,智能體穿過(guò)欄桿的概率為0.5。該隨機(jī)博弈一共包含7個(gè)狀態(tài)。這個(gè)博弈的納什均衡策略是,每個(gè)智能體到達(dá)鄰居位置而不穿過(guò)欄桿。
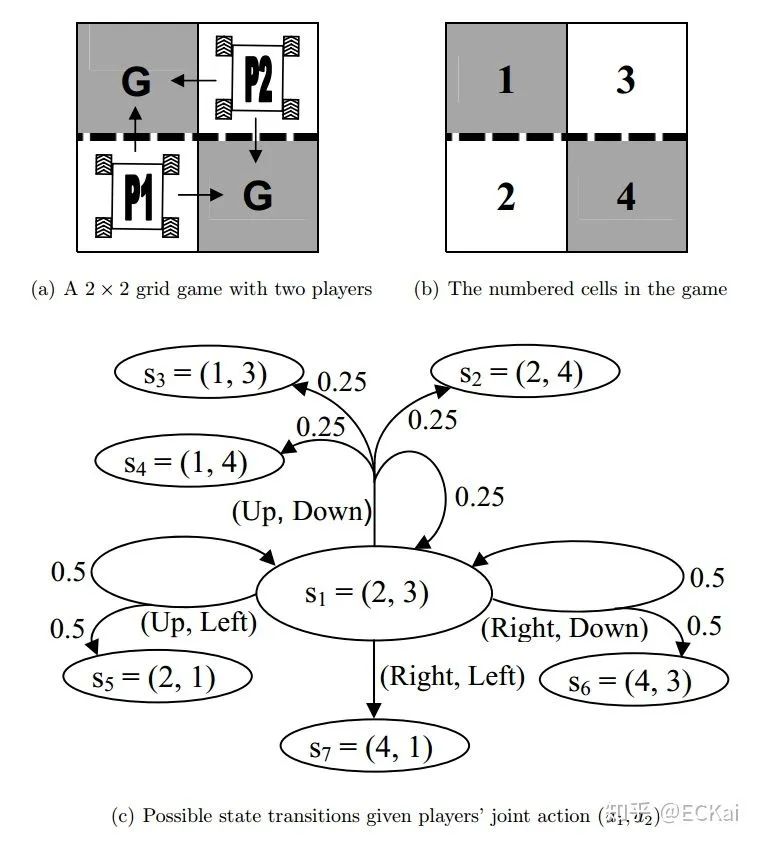
根據(jù)前文公式,我們可以得到如下?tīng)顟B(tài)值函數(shù)

由此我們可以得到動(dòng)作狀態(tài)值函數(shù)


求解上述矩陣博弈就可得到多智能體強(qiáng)化學(xué)習(xí)的策略。

尊敬的讀者你好,我們建立了微信群,方便大家學(xué)習(xí)交流討論!歡迎大家!
另外微商和廣告商請(qǐng)繞道!謝謝合作!
不能進(jìn)群的朋友請(qǐng)加我的微信!

