聯(lián)合概率和條件概率的區(qū)別和聯(lián)系
來源:DeepHub IMBA 本文約2300字,建議閱讀9分鐘
本文為你解釋聯(lián)合概率和條件概率之間區(qū)別和聯(lián)系。
聯(lián)合概率P(A∩B)
P(A ∩ B) = P(A) ? P(B)
P(A ∩ B) = P(A) ? P(B|A)
聯(lián)合概率和條件概率
用維恩圖理解
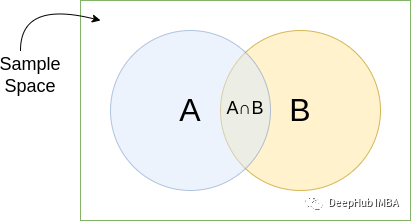
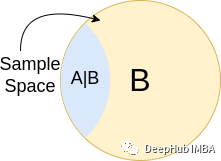
??(??∣??) ≥??(??∩??)
更多的例子


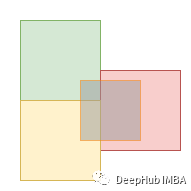

大約62%的女性選擇隱身作為她們的超能力。 在選擇隱身作為自己超能力的人中,大約有62%是女性。

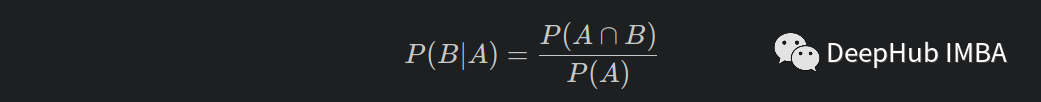
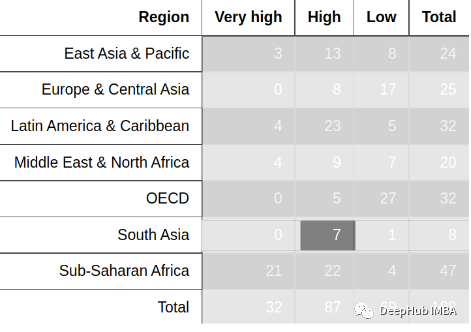
總結(jié)
推薦閱讀
學(xué)習(xí)機(jī)器學(xué)習(xí)的最佳路徑
評論
圖片
表情
