道阻且長(zhǎng)_再探矩陣乘法優(yōu)化
【GiantPandaCV導(dǎo)語(yǔ)】本文記錄了筆者最近的一些優(yōu)化gemm的思路和實(shí)現(xiàn),這些思路大多是公開的方案,例如來自how-to-optimize-gemm工程的一些優(yōu)化手段,來自ncnn的一些優(yōu)化手段等。最終,筆者目前實(shí)現(xiàn)的版本在armv7a上可以達(dá)到50%左右的硬件利用率(這個(gè)利用率的確還不高,筆者也是一步步學(xué)習(xí)和嘗試,大佬輕噴),本文記錄了這些思路以及核心實(shí)現(xiàn)方法。改好的行主序代碼(x86+armv7a版本)可以直接訪問https://github.com/BBuf/how-to-optimize-gemm獲取。
1. 前言
首先,我想強(qiáng)調(diào)一點(diǎn),判斷一個(gè)算法的加速效果和速度一定要實(shí)測(cè),盡量不要全信別人給出的benchmark數(shù)據(jù),做任何事都需要靜心一步步來。這篇文章是在基于how-to-optimize-gemm初探矩陣乘法優(yōu)化的基礎(chǔ)上做了更加精細(xì)的測(cè)試,另外參考了NCNN的卷積思路最后在單核A53上獲得了45%的硬件利用率,如果將輸入數(shù)據(jù)的Pack也提前做掉(類似于NC4HW4輸入),則可以獲得50%以上的硬件利用率。因此這篇文章將從上面介紹的各個(gè)優(yōu)化點(diǎn)進(jìn)行解析,并且此算法的最優(yōu)版本已經(jīng)集成到Msnhnet(https://github.com/msnh2012/Msnhnet),讀者也可以在里面看到。接下來我就直接介紹這一系列優(yōu)化手段。
如果讀者想具體看某一種優(yōu)化的優(yōu)化效果以及對(duì)應(yīng)的代碼實(shí)現(xiàn),可以直接參考下面的結(jié)果表格(基于armv7a的結(jié)果),然后去https://github.com/BBuf/how-to-optimize-gemm/tree/master/armv7a/src下選擇對(duì)應(yīng)的源碼文件查看即可:
| 文件名 | 優(yōu)化方法 | gFLOPs | 峰值占比 | 線程數(shù) |
|---|---|---|---|---|
| MMult1.h | 無任何優(yōu)化 | 0.24gflops | 2.1% | 1 |
| MMult2.h | 一次計(jì)算4個(gè)元素 | 0.24gflops | 2.1% | 1 |
| MMult_1x4_3.h | 一次計(jì)算4個(gè)元素 | 0.24gflops | 2.1% | 1 |
| MMult_1x4_4.h | 一次計(jì)算4個(gè)元素 | 0.24gflops | 2.1% | 1 |
| MMult_1x4_5.h | 一次計(jì)算4個(gè)元素(將4個(gè)循環(huán)合并為1個(gè)) | 0.25gflops | 2.2% | 1 |
| MMult_1x4_7.h | 一次計(jì)算4個(gè)元素(我們?cè)诩拇嫫髦欣奂覥的元素,并對(duì)a的元素使用寄存器),用指針來尋址B中的元素 | 0.98gflops | 9.0% | 1 |
| MMult_1x4_8.h | 在MMult_1x4_7的基礎(chǔ)上循環(huán)展開四個(gè)(展開因子的相對(duì)任意選擇) | 1.1gflops | 10% | 1 |
| MMult_4x4_3.h | 一次計(jì)算C中的4x4小塊 | 0.24gflops | 2.1% | 1 |
| MMult_4x4_4.h | 一次計(jì)算C中的4x4小塊 | 0.24gflops | 2.1% | 1 |
| MMult_4x4_5.h | 一次計(jì)算C中的4x4小塊,將16個(gè)循環(huán)合并一個(gè) | 0.25gflops | 2.2% | 1 |
| MMult_4x4_6.h | 一次計(jì)算C中的4x4小塊(我們?cè)诩拇嫫髦欣奂覥的元素,并對(duì)a的元素使用寄存器) | 1.75gflops | 16.0% | 1 |
| MMult_4x4_7.h | 在MMult_4x4_6的基礎(chǔ)上用指針來尋址B中的元素 | 1.75gflops | 16.0% | 1 |
| MMult_4x4_8.h | 使用更多的寄存器 | 1.75gflops | 16.0% | 1 |
| MMult_4x4_10.h | NEON指令集優(yōu)化 | 2.6gflops | 23.8% | 1 |
| MMult_4x4_11.h | NEON指令集優(yōu)化, 并且為了保持較小問題規(guī)模所獲得的性能,我們分塊矩陣C(以及相應(yīng)的A和B) | 2.6gflops | 23.8% | 1 |
| MMult_4x4_13.h | NEON指令集優(yōu)化, 對(duì)矩陣A和B進(jìn)行Pack,這樣就可以連續(xù)訪問內(nèi)存 | 2.6gflops | 23.8% | 1 |
| conv1x1s1.h(version1) | 一次計(jì)算多行,neon匯編優(yōu)化 | 3.4gflops | 31.0% | 1 |
| conv1x1s1.h(version2) | pack,kernel提前做,neon匯編優(yōu)化 | 4.9gflops | 45% | 1 |
| conv1x1s1.h(version3) | pack,kernel提前做,輸入NC4HW4,neon匯編優(yōu)化 | 5.5gflops | 50.5% | 1 |
為了大家看起來不累,這篇文章盡量不粘貼大段代碼,我主要為大家介紹思路,代碼可以到上面提供的源碼倉(cāng)庫(kù)中查看。
2. 原始實(shí)現(xiàn)
這個(gè)非常簡(jiǎn)單,就是實(shí)現(xiàn),其中的維度是,的維度是,的維度是,那么矩陣乘法的原始實(shí)現(xiàn)就是(注意,這里是行主序):
#define?A(?i,?j?)?a[?(i)*lda?+?(j)?]
#define?B(?i,?j?)?b[?(i)*ldb?+?(j)?]
#define?C(?i,?j?)?c[?(i)*ldb?+?(j)?]
//?gemm?C?=?A?*?B?+?C
void?MatrixMultiply(int?m,?int?n,?int?k,?float?*a,?int?lda,?float?*b,?int?ldb,?float?*c,?int?ldc)
{
????for(int?i?=?0;?i?????????for?(int?j=0;?j????????????for?(int?p=0;?p????????????????C(i,?j)?=?C(i,?j)?+?A(i,?p)?*?B(p,?j);
????????????}
????????}
????}
}
這一個(gè)版本的gflops只有0.24g,硬件利用率只有1.4%,接下來我們就逐步進(jìn)行優(yōu)化。
3. 一次計(jì)算4個(gè)元素
這里一次計(jì)算4個(gè)元素的意思是一次計(jì)算矩陣也就是結(jié)果矩陣的個(gè)元素。在第二節(jié)的原始實(shí)現(xiàn)中,我們一次計(jì)算矩陣的一個(gè)元素,這個(gè)時(shí)候需要遍歷A矩陣的一行和B矩陣的一列并做乘加運(yùn)算。如果我們一次計(jì)算C矩陣的4個(gè)元素,那么我們可以每次遍歷A矩陣的一行和B矩陣的四列,代碼實(shí)現(xiàn)大概是這個(gè)樣子:
void?MY_MMult2(?int?m,?int?n,?int?k,?float?*a,?int?lda,?
????????????????????????????????????float?*b,?int?ldb,
????????????????????????????????????float?*c,?int?ldc?){
??int?i,?j;
??for?(?j=0;?j4?){
????for?(?i=0;?i1?){
??????AddDot(?k,?&A(?i,0?),?lda,?&B(?0,j?),?&C(?i,j?)?);
??????AddDot(?k,?&A(?i,0?),?lda,?&B(?0,j+1?),?&C(?i,j+1?)?);
??????AddDot(?k,?&A(?i,0?),?lda,?&B(?0,j+2?),?&C(?i,j+2?)?);
??????AddDot(?k,?&A(?i,0?),?lda,?&B(?0,j+3?),?&C(?i,j+3?)?);
????}
??}
}
但是很遺憾,由于編譯器開了O2,這種優(yōu)化方法并不奏效,這個(gè)版本取得了和原始實(shí)現(xiàn)差不多的gflops。
4. 第一次還算有效的優(yōu)化
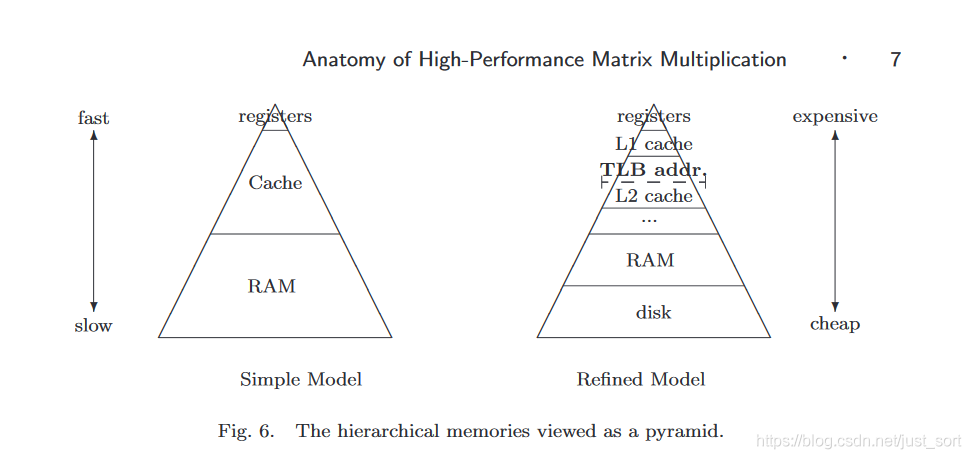
第一次看起來比較有效的方法是引入寄存器變量。從計(jì)算機(jī)存儲(chǔ)體系結(jié)構(gòu)圖(Figure3)可以看到寄存器變量離CPU是最近的,它的數(shù)據(jù)訪問數(shù)據(jù)也是最快的,因此我們可以在求和的時(shí)候顯示聲明求和和被乘的變量為寄存器變量,這樣在累加求和的時(shí)候訪問速度會(huì)比原始版本更快一些,可以帶來一些提升。
 這部分的代碼實(shí)現(xiàn)大致如下:
這部分的代碼實(shí)現(xiàn)大致如下:
void?AddDot1x4(?int?k,?float?*a,?int?lda,??float?*b,?int?ldb,?float?*c,?int?ldc?){
??int?p;
??register?float?c_00_reg,?c_01_reg,?c_02_reg,?c_03_reg,???a_0p_reg;
??c_00_reg?=?0.0;?
??c_01_reg?=?0.0;?
??c_02_reg?=?0.0;?
??c_03_reg?=?0.0;
??for?(?p=0;?p????a_0p_reg?=?A(?0,?p?);
????c_00_reg?+=?a_0p_reg?*?B(?p,?0?);?????
????c_01_reg?+=?a_0p_reg?*?B(?p,?1?);?????
????c_02_reg?+=?a_0p_reg?*?B(?p,?2?);?????
????c_03_reg?+=?a_0p_reg?*?B(?p,?3?);?????
??}
??C(?0,?0?)?+=?c_00_reg;?
??C(?0,?1?)?+=?c_01_reg;?
??C(?0,?2?)?+=?c_02_reg;?
??C(?0,?3?)?+=?c_03_reg;
}
這個(gè)版本的代碼對(duì)應(yīng)https://github.com/BBuf/how-to-optimize-gemm/blob/master/armv7a/src/MMult_1x4x6.h,取得了0.32gflops的成績(jī),在原始版本上有微弱提升。
5. 第一次提升較大的優(yōu)化
在第一次優(yōu)化的基礎(chǔ)上,我們用指針來尋址A中的元素。因?yàn)檫@里實(shí)現(xiàn)的是行主序的矩陣乘法,因此每計(jì)算一個(gè)C中元素,對(duì)于A的任意一行的內(nèi)存訪問都是連續(xù)的,這樣我們就可以用指針移位的方式代替數(shù)據(jù)訪問的方式了。基于這個(gè)思路,我們可以將第4節(jié)的代碼改寫成下面的樣子:
void?AddDot1x4(?int?k,?float?*a,?int?lda,??float?*b,?int?ldb,?float?*c,?int?ldc?){
??int?p;
??register?float?c_00_reg,???c_01_reg,???c_02_reg,???c_03_reg,??b_0p_reg;
??float?*ap0_pntr,?*ap1_pntr,?*ap2_pntr,?*ap3_pntr;
??ap0_pntr?=?&A(?0,?0?);
??ap1_pntr?=?&A(?1,?0?);
??ap2_pntr?=?&A(?2,?0?);
??ap3_pntr?=?&A(?3,?0?);
??c_00_reg?=?0.0;?
??c_01_reg?=?0.0;?
??c_02_reg?=?0.0;?
??c_03_reg?=?0.0;
??for?(?p=0;?p????b_0p_reg?=?B(?p,?0?);
????c_00_reg?+=?b_0p_reg?*?*ap0_pntr++;
????c_01_reg?+=?b_0p_reg?*?*ap1_pntr++;
????c_02_reg?+=?b_0p_reg?*?*ap2_pntr++;
????c_03_reg?+=?b_0p_reg?*?*ap3_pntr++;
??}
??C(?0,?0?)?+=?c_00_reg;?
??C(?1,?0?)?+=?c_01_reg;?
??C(?2,?0?)?+=?c_02_reg;?
??C(?3,?0?)?+=?c_03_reg;
}
這樣一個(gè)小的改動(dòng),我們獲得了0.98gflops,硬件利用率來到了9%,這確實(shí)是一個(gè)提升較大的優(yōu)化。這個(gè)版本的代碼對(duì)應(yīng)https://github.com/BBuf/how-to-optimize-gemm/blob/master/armv7a/src/MMult_1x4_7.h 。
6. 第三次優(yōu)化,嘗試更大的分塊
在上面的幾次優(yōu)化中,我們一次計(jì)算C矩陣的一個(gè)元素或者C矩陣的4個(gè)元素,我們這一節(jié)將其擴(kuò)展為一次計(jì)算C矩陣的16個(gè)元素,即分塊方法。另外,我們使用寄存器變量累加C的元素,并對(duì)A的元素也使用寄存器變量。這部分代碼實(shí)現(xiàn)也比較簡(jiǎn)單,可以在https://github.com/BBuf/how-to-optimize-gemm/blob/master/armv7a/src/MMult_4x4_6.h查看。經(jīng)過分塊后,我們獲得了1.75gflops的結(jié)果,硬件利用率在16%左右。
接下來,參考第5節(jié)的思路,我們?cè)?code style="font-size: 14px;word-wrap: break-word;padding: 2px 4px;border-radius: 4px;margin: 0 2px;color: #1e6bb8;background-color: rgba(27,31,35,.05);font-family: Operator Mono, Consolas, Monaco, Menlo, monospace;word-break: break-all;">/MMult_4x4_6的基礎(chǔ)上用指針來尋址B中的元素,但因?yàn)?span style="cursor:pointer;">分塊本身對(duì)內(nèi)存訪問就有很大的改善,這個(gè)優(yōu)化在這里作用不大。沒有獲得明顯的gflops提升。這部分的代碼實(shí)現(xiàn)對(duì)應(yīng)https://github.com/BBuf/how-to-optimize-gemm/blob/master/armv7a/src/MMult_4x4_7.h
7. 第四次優(yōu)化,Neon指令集優(yōu)化
在計(jì)算C中的元素時(shí),我們可以使用simd來進(jìn)行優(yōu)化,在Armv7a架構(gòu)上即是將https://github.com/BBuf/how-to-optimize-gemm/blob/master/armv7a/src/MMult_4x4_10.h的核心實(shí)現(xiàn)部分用Neon指令集來進(jìn)行優(yōu)化,這里先使用Neon Instrics進(jìn)行優(yōu)化。
void?AddDot4x4(?int?k,?float?*a,?int?lda,??float?*b,?int?ldb,?float?*c,?int?ldc?){
??float??*a_0p_pntr,?*a_1p_pntr,?*a_2p_pntr,?*a_3p_pntr;
??a_0p_pntr?=?&A(0,?0);
??a_1p_pntr?=?&A(1,?0);
??a_2p_pntr?=?&A(2,?0);
??a_3p_pntr?=?&A(3,?0);
??float32x4_t?c_p0_sum?=?{0};
??float32x4_t?c_p1_sum?=?{0};
??float32x4_t?c_p2_sum?=?{0};
??float32x4_t?c_p3_sum?=?{0};
??register?float?a_0p_reg,?a_1p_reg,?a_2p_reg,?a_3p_reg;
??for?(int?p?=?0;?p?????float32x4_t?b_reg?=?vld1q_f32(&B(p,?0));
????a_0p_reg?=?*a_0p_pntr++;
????a_1p_reg?=?*a_1p_pntr++;
????a_2p_reg?=?*a_2p_pntr++;
????a_3p_reg?=?*a_3p_pntr++;
????c_p0_sum?=?vmlaq_n_f32(c_p0_sum,?b_reg,?a_0p_reg);
????c_p1_sum?=?vmlaq_n_f32(c_p1_sum,?b_reg,?a_1p_reg);
????c_p2_sum?=?vmlaq_n_f32(c_p2_sum,?b_reg,?a_2p_reg);
????c_p3_sum?=?vmlaq_n_f32(c_p3_sum,?b_reg,?a_3p_reg);
??}
??float?*c_pntr?=?0;
??c_pntr?=?&C(0,?0);
??float32x4_t?c_reg?=?vld1q_f32(c_pntr);
??c_reg?=?vaddq_f32(c_reg,?c_p0_sum);
??vst1q_f32(c_pntr,?c_reg);
??c_pntr?=?&C(1,?0);
??c_reg?=?vld1q_f32(c_pntr);
??c_reg?=?vaddq_f32(c_reg,?c_p1_sum);
??vst1q_f32(c_pntr,?c_reg);
??c_pntr?=?&C(2,?0);
??c_reg?=?vld1q_f32(c_pntr);
??c_reg?=?vaddq_f32(c_reg,?c_p2_sum);
??vst1q_f32(c_pntr,?c_reg);
??c_pntr?=?&C(3,?0);
??c_reg?=?vld1q_f32(c_pntr);
??c_reg?=?vaddq_f32(c_reg,?c_p3_sum);
??vst1q_f32(c_pntr,?c_reg);
}
之前和德澎在《AI移動(dòng)端優(yōu)化》專欄里面介紹過很多Neon指令集優(yōu)化的例子,所以這里就不再詳細(xì)上面的代碼每行代表什么意思了,感興趣的讀者可以對(duì)比MMult_4x4_7.h的代碼來理解。經(jīng)過Neon Instrics優(yōu)化之后,我們獲得了2.6gflops的成績(jī),達(dá)到了23.8%的硬件利用率。
8. 第5次優(yōu)化,數(shù)據(jù)Pack
在上面的優(yōu)化中我們可以發(fā)現(xiàn),在矩陣乘法的計(jì)算中,無論是行主序還是列主序,始終有一個(gè)矩陣的內(nèi)存是沒辦法連續(xù)訪問的。這也是為什么我們分塊后gflops能獲得較大提升的重要原因。因此,為了改善這個(gè)情況,我們執(zhí)行數(shù)據(jù)Pack,將矩陣A和矩陣B的訪問時(shí)的內(nèi)存變成連續(xù)的。
理論上來說,這樣做一定是有提升的,但是在Armv7a上實(shí)測(cè)發(fā)現(xiàn)gflops并沒有提升(在x86上有4倍左右的gflops提升)。這里的原因猜測(cè)主要是Pack數(shù)據(jù)本身也需要時(shí)間,另外的分塊已經(jīng)較好的規(guī)避了內(nèi)存不連續(xù)導(dǎo)致的訪存時(shí)間消耗,當(dāng)數(shù)據(jù)Pack的時(shí)間不可忽略時(shí)加速就非常少,而x86架構(gòu)下的數(shù)據(jù)pack速度要優(yōu)于armv7a架構(gòu)(猜測(cè),如果大佬有更好的解釋,請(qǐng)聯(lián)系我)。
因此,這里給我的啟發(fā)是數(shù)據(jù)Pack盡量要在核心計(jì)算過程的外部完成。
9. 第6次優(yōu)化,一次計(jì)算多行+Neon Assembly
首先我們知道,在CNN中卷積可以直接看成Kernel矩陣和輸入特征圖矩陣直接做矩陣乘法,我們可以把的卷積核看成矩陣乘法的矩陣A,它的維度是。然后再把輸入特征圖看成矩陣乘法的矩陣B,它的維度是,這樣矩陣C就是我們的卷積結(jié)果了,維度是,因?yàn)?span style="cursor:pointer;">卷積并且步長(zhǎng)為的情況下輸出特征圖的長(zhǎng)寬和輸入特征圖是完全一致的。
其中:
inChannel 表示卷積層的輸入通道數(shù) outChanenel 表示卷積層的輸出通道數(shù) inHeight 表示輸入特征圖的高度 inWidth 表示輸入特征圖的寬度
基于此,我參考了NCNN的卷積的第一版實(shí)現(xiàn)方法獲得了本次優(yōu)化的版本。完整實(shí)現(xiàn)在https://github.com/BBuf/how-to-optimize-gemm/blob/master/armv7a/src/convolution1x1s1.h#L10。主要思路就是一次計(jì)算行的輸出,并且在每一行使用Neon指令集(Neon Assembly)進(jìn)行優(yōu)化,即在列方向再一次計(jì)算個(gè)元素。為了更好理解這個(gè)思路,下面我將這個(gè)函數(shù)Neon優(yōu)化相關(guān)的部分去掉,留下了一個(gè)普通實(shí)現(xiàn)的代碼如下,可以幫助讀者快速理解這個(gè)算法。
void?conv1x1s1(float?*const?&src,?const?int?&inWidth,?const?int?&inHeight,??const?int?&inChannel,?float?*const?&kernel,
?????????????????????????????????float*?&dest,?const?int?&outWidth,?const?int?&outHeight,?const?int?&outChannel){
????????int?ccOutChannel?=?outChannel?>>?2;
????????int?ccRemainOutChannel?=?ccOutChannel?<2;
????????const?int?in_size?=?inWidth?*?inHeight;
????????const?int?out_size?=?outWidth?*?outHeight;
????????for(int?cc?=?0;?cc?????????????int?c?=?cc?<2;
????????????
????????????float?*dest0?=?dest?+?c?*?out_size;
????????????float?*dest1?=?dest?+?(c?+?1)?*?out_size;
????????????float?*dest2?=?dest?+?(c?+?2)?*?out_size;
????????????float?*dest3?=?dest?+?(c?+?3)?*?out_size;
????????????int?q?=?0;
????????????for(q?=?0;?q?+?3?4){
????????????????float?*destptr0?=?dest0;
????????????????float?*destptr1?=?dest1;
????????????????float?*destptr2?=?dest2;
????????????????float?*destptr3?=?dest3;
????????????????const?float?*src0?=?src?+?q?*?in_size;
????????????????const?float?*src1?=?src?+?(q?+?1)?*?in_size;
????????????????const?float?*src2?=?src?+?(q?+?2)?*?in_size;
????????????????const?float?*src3?=?src?+?(q?+?3)?*?in_size;
????????????????const?float?*r0?=?src0;
????????????????const?float?*r1?=?src1;
????????????????const?float?*r2?=?src2;
????????????????const?float?*r3?=?src3;
????????????????const?float?*kernel0?=?kernel?+?c?*?inChannel?+?q;
????????????????const?float?*kernel1?=?kernel?+?(c?+?1)?*?inChannel?+?q;
????????????????const?float?*kernel2?=?kernel?+?(c?+?2)?*?inChannel?+?q;
????????????????const?float?*kernel3?=?kernel?+?(c?+?3)?*?inChannel?+?q;
????????????????int?remain?=?out_size;
????????????????for(;?remain?>?0;??remain--){
????????????????????float?sum0?=?*r0?*?kernel0[0]?+?*r1?*?kernel0[1]?+?*r2?*?kernel0[2]?+?*r3?*?kernel0[3];
????????????????????float?sum1?=?*r0?*?kernel1[0]?+?*r1?*?kernel1[1]?+?*r2?*?kernel1[2]?+?*r3?*?kernel1[3];
????????????????????float?sum2?=?*r0?*?kernel2[0]?+?*r1?*?kernel2[1]?+?*r2?*?kernel2[2]?+?*r3?*?kernel2[3];
????????????????????float?sum3?=?*r0?*?kernel3[0]?+?*r1?*?kernel3[1]?+?*r2?*?kernel3[2]?+?*r3?*?kernel3[3];
????????????????????*destptr0?+=?sum0;
????????????????????*destptr1?+=?sum1;
????????????????????*destptr2?+=?sum2;
????????????????????*destptr3?+=?sum3;
????????????????????r0++;
????????????????????r1++;
????????????????????r2++;
????????????????????r3++;
????????????????????destptr0++;
????????????????????destptr1++;
????????????????????destptr2++;
????????????????????destptr3++;
????????????????}
????????????}
????????????for(;?q?????????????????float?*destptr0?=?dest0;
????????????????float?*destptr1?=?dest1;
????????????????float?*destptr2?=?dest2;
????????????????float?*destptr3?=?dest3;
????????????????const?float?*src0?=?src?+?q?*?in_size;
????????????????const?float?*kernel0?=?kernel?+?c?*?inChannel?+?q;
????????????????const?float?*kernel1?=?kernel?+?(c?+?1)?*?inChannel?+?q;
????????????????const?float?*kernel2?=?kernel?+?(c?+?2)?*?inChannel?+?q;
????????????????const?float?*kernel3?=?kernel?+?(c?+?3)?*?inChannel?+?q;
????????????????const?float?*r0?=?src0;
????????????????int?remain?=?out_size;
????????????????for(;?remain?>?0;?remain--){
????????????????????float?sum0?=?*r0?*?kernel0[0];
????????????????????float?sum1?=?*r0?*?kernel1[0];
????????????????????float?sum2?=?*r0?*?kernel2[0];
????????????????????float?sum3?=?*r0?*?kernel3[0];
????????????????????*destptr0?+=?sum0;
????????????????????*destptr1?+=?sum1;
????????????????????*destptr2?+=?sum2;
????????????????????*destptr3?+=?sum3;
????????????????????r0++;
????????????????????destptr0++;
????????????????????destptr1++;
????????????????????destptr2++;
????????????????????destptr3++;
????????????????}
????????????}
????????}
????????for(int?cc?=?ccRemainOutChannel;?cc?????????????float?*dest0?=?dest?+?cc?*?out_size;
????????????int?q?=?0;
????????????for(;?q?+?3?4){
????????????????float?*destptr0?=?dest0;
????????????????const?float?*src0?=?src?+?q?*?in_size;
????????????????const?float?*src1?=?src?+?(q?+?1)?*?in_size;
????????????????const?float?*src2?=?src?+?(q?+?2)?*?in_size;
????????????????const?float?*src3?=?src?+?(q?+?3)?*?in_size;
????????????????const?float?*r0?=?src0;
????????????????const?float?*r1?=?src1;
????????????????const?float?*r2?=?src2;
????????????????const?float?*r3?=?src3;
????????????????const?float?*kernel0?=?kernel?+?cc?*?inChannel?+?q;
????????????????int?remain?=?out_size;
????????????????for(;?remain?>?0;?remain--){
????????????????????float?sum0?=?*r0?*?kernel0[0]?+?*r1?*?kernel0[1]?+?*r2?*?kernel0[2]?+?*r3?*?kernel0[3];
????????????????????*destptr0?+=?sum0;
????????????????????r0++;
????????????????????r1++;
????????????????????r2++;
????????????????????r3++;
????????????????????destptr0++;
????????????????}
????????????}
????????????for(;?q?????????????????float?*destptr0?=?dest0;
????????????????const?float?*src0?=?src?+?q?*?in_size;
????????????????const?float?*kernel0?=?kernel?+?cc?*?inChannel?+?q;
????????????????const?float?*r0?=?src0;
????????????????int?remain?=?out_size;
????????????????for(;?remain?>?0;?remain--){
????????????????????float?sum0?=?*r0?*?kernel0[0];
????????????????????*destptr0?+=?sum0;
????????????????????r0++;
????????????????????destptr0++;
????????????????}
????????????}
????????}
}
將上面的代碼進(jìn)行Neon Assembly優(yōu)化然后進(jìn)行測(cè)試,我們獲得了3.4gflops的成績(jī),硬件利用率達(dá)到了31%,是當(dāng)前的最好成績(jī)。
10. 第7次優(yōu)化,數(shù)據(jù)Pack顯威力
由于第6次優(yōu)化的實(shí)現(xiàn)并未考慮到數(shù)據(jù)Pack的原因,所以訪存是比較差的,這里可以使用Pack策略對(duì)其進(jìn)行優(yōu)化。這個(gè)思路我已經(jīng)在詳解Im2Col+Pack+Sgemm策略更好的優(yōu)化卷積運(yùn)算 用各種圖例講得還算清楚了,另外MsnhNet的作者之前也做過一篇關(guān)于NC4HW4的圖解圖解神秘的NC4HW4,所以這里不再重復(fù)數(shù)據(jù)Pack的好處以及我這里具體是如何做數(shù)據(jù)Pack的,感興趣的請(qǐng)直接移步源碼。
將卷積核進(jìn)行數(shù)據(jù)Pack(只用做一次,不會(huì)影響gflops),然后對(duì)輸入數(shù)據(jù)進(jìn)行Pack(注意Version2是每次計(jì)算過程都要做一次輸入數(shù)據(jù)的Pack,所以數(shù)據(jù)輸入Pack的時(shí)間也會(huì)影響gflops),然后進(jìn)行計(jì)算。這部分的代碼實(shí)現(xiàn)在https://github.com/msnh2012/Msnhnet/blob/master/src/layers/arm/MsnhConvolution1x1.cpp#L598。
對(duì)這個(gè)版本進(jìn)行測(cè)試,我們獲得了4.9gflops的成績(jī),達(dá)到了硬件利用率的49.5%。
另外,我們考慮一下如果將輸入的排布變成NC4HW4的方式,那么輸入數(shù)據(jù)的Pack時(shí)間也可以省掉,通過這樣操作,我獲得了5.5gflops的結(jié)果,達(dá)到了硬件利用率的50.5%。代碼實(shí)現(xiàn)在:https://github.com/BBuf/how-to-optimize-gemm/blob/master/armv7a/src/convolution1x1s1.h 。
11. 總結(jié)
這篇文章主要是記錄一下這兩周對(duì)gemm算法優(yōu)化的一些研究,然后我是如何一步步將矩陣乘法的硬件利用率做到了50%。當(dāng)然,這個(gè)硬件利用率并不高,我也會(huì)持續(xù)學(xué)習(xí)和優(yōu)化,歡迎大家提出建議和關(guān)注我們公眾號(hào)GiantPandaCV,您的關(guān)注是我最大的鼓勵(lì)。
12. 參考鏈接
https://github.com/Tencent/ncnn https://github.com/tpoisonooo/how-to-optimize-gemm/tree/master/src/HowToOptimizeGemm https://github.com/flame/blislab https://github.com/msnh2012/Msnhnet
歡迎關(guān)注GiantPandaCV, 在這里你將看到獨(dú)家的深度學(xué)習(xí)分享,堅(jiān)持原創(chuàng),每天分享我們學(xué)習(xí)到的新鮮知識(shí)。( ? ?ω?? )?
有對(duì)文章相關(guān)的問題,或者想要加入交流群,歡迎添加BBuf微信:
為了方便讀者獲取資料以及我們公眾號(hào)的作者發(fā)布一些Github工程的更新,我們成立了一個(gè)QQ群,二維碼如下,感興趣可以加入。
