提升分類模型acc(三):優(yōu)化調(diào)參

一、前言
這是本系列的第三篇文章,前兩篇主要是講怎么取得速度&精度的平衡以及一些常用的調(diào)參技巧,本文主要結合自身經(jīng)驗講解一些輔助訓練的手段和技術。
往期文章回顧:
提升分類模型acc(一):BatchSize&LARS 提升分類模型acc(二):Bag of Tricks
二、Tricks
本文主要分一下幾個方向來進行講解
權重平均 蒸餾 分辨率
2.1 權重平均
由于深度學習訓練往往不能找到全局最優(yōu)解,大部分的時間都是在局部最優(yōu)來回的晃動,我們所取得到的權重很可能是局部最優(yōu)的最差的那一個,所以一個解決的辦法就是把這幾個局部最優(yōu)解拿過來,做一個均值操作,再讓網(wǎng)絡加載這個權重進行預測,那么有了這個思想,就衍生了如下的權重平均的方法。
1. EMA
指數(shù)移動平均(Exponential Moving Average)也叫權重移動平均(Weighted Moving Average),是一種給予近期數(shù)據(jù)更高權重的平均方法。(PS: EMA是統(tǒng)計學常用的方法,不要以為是DL才有的,DL只是拿來用到了權重上和求bn的mean和std上)
公式如下:
假設有n個數(shù):
EMA: ,其中, 表示前 條的平均值 ( ), 是加權權重值 (一般設為0.9-0.999)。
這里的就是表示的是模型權重,則表示的是影子權重,影子權重不參與訓練。
代碼如下:
class?ModelEma(nn.Module):
????def?__init__(self,?model,?decay=0.9999,?device=None):
????????super(ModelEma,?self).__init__()
????????#?make?a?copy?of?the?model?for?accumulating?moving?average?of?weights
????????self.module?=?deepcopy(model)
????????self.module.eval()
????????self.decay?=?decay
????????self.device?=?device??#?perform?ema?on?different?device?from?model?if?set
????????if?self.device?is?not?None:
????????????self.module.to(device=device)
????def?_update(self,?model,?update_fn):
????????with?torch.no_grad():
????????????for?ema_v,?model_v?in?zip(self.module.state_dict().values(),?model.state_dict().values()):
????????????????if?self.device?is?not?None:
????????????????????model_v?=?model_v.to(device=self.device)
????????????????ema_v.copy_(update_fn(ema_v,?model_v))
????def?update(self,?model):
????????self._update(model,?update_fn=lambda?e,?m:?self.decay?*?e?+?(1.?-?self.decay)?*?m)
????def?set(self,?model):
????????self._update(model,?update_fn=lambda?e,?m:?m)
EMA的好處是在于不需要增加額外的訓練時間,也不需要手動調(diào)參,只需要在測試階段,多進行幾組測試挑選最好偶的結果即可。不過是否真的具有提升,還是和具體任務相關,比賽的話可以多加嘗試。
2. SWA
隨機權重平均(Stochastic Weight Averaging),SWA是一種通過隨機梯度下降改善深度學習模型泛化能力的方法,而且這種方法不會為訓練增加額外的消耗,這種方法可以嵌入到Pytorch中的任何優(yōu)化器類中。
具有如下幾個特點:
SWA可以改進模型訓練過程的穩(wěn)定性; SWA的擴展方法可以達到高精度的貝葉斯模型平均的效果,同時對深度學習模型進行校準; 即便是在低精度(int8)下訓練的SWA,即SWALP,也可以達到全精度下SGD訓練的效果。
由于pytroch已經(jīng)實現(xiàn)了SWA,所以可以直接使用,代碼如下:
from?torchcontrib.optim?import?SWA
...
...
#?training?loop
base_opt?=?torch.optim.SGD(model.parameters(),?lr=0.1)
opt?=?torchcontrib.optim.SWA(base_opt,?swa_start=10,?swa_freq=5,?swa_lr=0.05)
for?_?in?range(100):
?????opt.zero_grad()
?????loss_fn(model(input),?target).backward()
?????opt.step()
opt.swap_swa_sgd()
這里可以使用任何的優(yōu)化器,不局限于SGD,訓練結束后可以使用swap_swa_sgd()來觀察模型對應的SWA權重。
SWA能夠work的關鍵有兩點:
SWA采用改良的學習率策略以便SGD能夠繼續(xù)探索能使模型表現(xiàn)更好的參數(shù)空間。比如,我們可以在訓練過程的前75%階段使用標準的學習率下降策略,在剩下的階段保持學習率不變。 將SGD經(jīng)過的參數(shù)進行平均。比如,可以將每個epoch最后25%訓練時間的權重進行平均。
可以看一下更新權重的代碼細節(jié):
class?AveragedModel(Module):
????def?__init__(self,?model,?device=None,?avg_fn=None):
????????super(AveragedModel,?self).__init__()
????????self.module?=?deepcopy(model)
????????if?device?is?not?None:
????????????self.module?=?self.module.to(device)
????????self.register_buffer('n_averaged',
?????????????????????????????torch.tensor(0,?dtype=torch.long,?device=device))
????????if?avg_fn?is?None:
????????????def?avg_fn(averaged_model_parameter,?model_parameter,?num_averaged):
????????????????return?averaged_model_parameter?+?\
????????????????????(model_parameter?-?averaged_model_parameter)?/?(num_averaged?+?1)
????????self.avg_fn?=?avg_fn
????def?forward(self,?*args,?**kwargs):
????????return?self.module(*args,?**kwargs)
????def?update_parameters(self,?model):
????????#?p_model?have?not?been?done
????????for?p_swa,?p_model?in?zip(self.parameters(),?model.parameters()):
????????????device?=?p_swa.device
????????????p_model_?=?p_model.detach().to(device)
????????????if?self.n_averaged?==?0:
????????????????p_swa.detach().copy_(p_model_)
????????????else:
????????????????p_swa.detach().copy_(self.avg_fn(p_swa.detach(),?p_model_,
?????????????????????????????????????????????????self.n_averaged.to(device)))
????????self.n_averaged?+=?1
可以看到,相比于EMA,SWA是可以選擇如何更新權重的方法,如果不傳入新的方法,則默認使用直接求平均的方法,也可以采用指數(shù)平均的方法。
由于SWA平均的權重在訓練過程中是不會用來預測的,所以當使用opt.swap_swa_sgd()重置權重之后,BN層相對應的統(tǒng)計信息仍然是之前權重的, 所以需要進行一次更新,代碼如下:
opt.bn_update(train_loader,?model)
這里可以引出一個關于bn的小trick
3. precise bn
由于BN在訓練和測試的時候,mean和std的更新是不一致的,如下圖: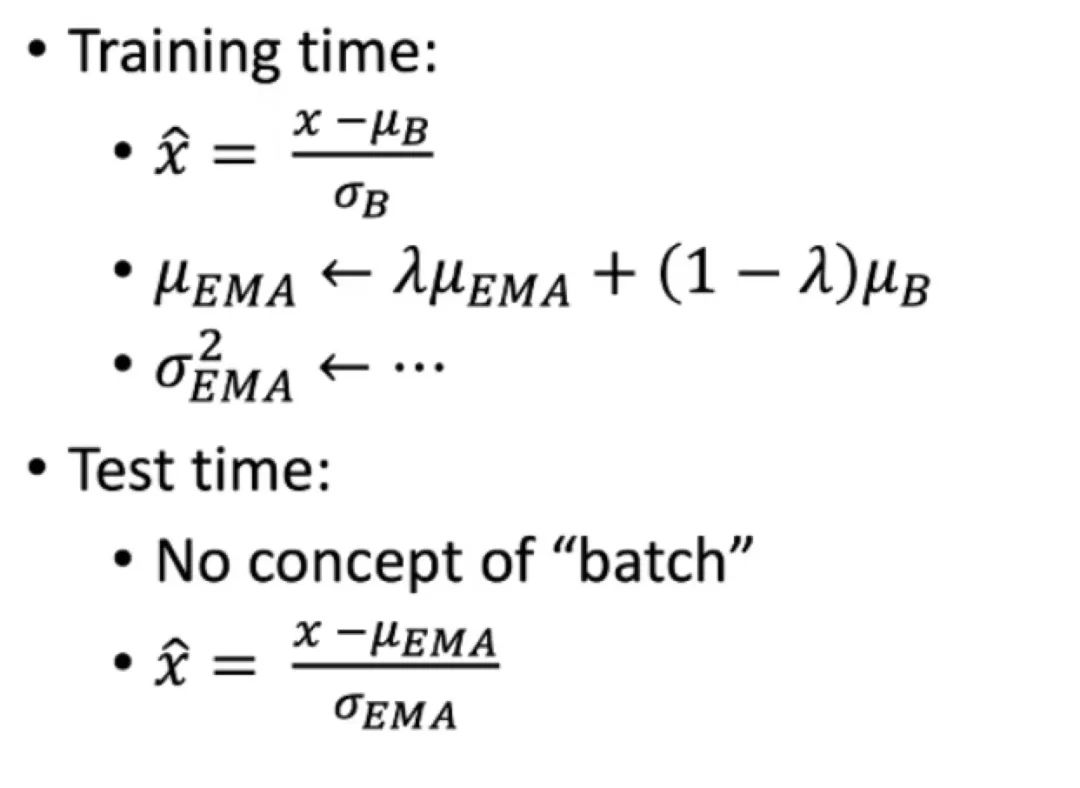 可以認為訓練的時候和我們做aug是類似的,增加“噪聲”, 使得模型可以學到的分布變的更廣。但是EMA并不是真的平均,如果數(shù)據(jù)的分布差異很大,那么就需要重新計算bn。簡單的做法如下:
可以認為訓練的時候和我們做aug是類似的,增加“噪聲”, 使得模型可以學到的分布變的更廣。但是EMA并不是真的平均,如果數(shù)據(jù)的分布差異很大,那么就需要重新計算bn。簡單的做法如下:
訓練一個epoch后,固定參數(shù) 然后將訓練數(shù)據(jù)輸入網(wǎng)絡做前向計算,保存每個step的均值和方差。 計算所有樣本的均值和方差。 測試。
代碼如下:
def?update_bn_stats(args:?Any,?model:?nn.Module,?data_loader:?Iterable[Any],?num_iters:?int?=?200??#?pyre-ignore
)?->?None:
????bn_layers?=?get_bn_modules(model)
????if?len(bn_layers)?==?0:
????????return
????momentum_actual?=?[bn.momentum?for?bn?in?bn_layers]
????if?args.rank?==?0:
????????a?=?[round(i.running_mean.cpu().numpy().max(),?4)?for?i?in?bn_layers]
????????logger.info('bn?mean?max,?%s',?max(a))
????????logger.info(a)
????????a?=?[round(i.running_var.cpu().numpy().max(),?4)?for?i?in?bn_layers]
????????logger.info('bn?var?max,?%s',?max(a))
????????logger.info(a)
????for?bn?in?bn_layers:
????????bn.momentum?=?1.0
????running_mean?=?[torch.zeros_like(bn.running_mean)?for?bn?in?bn_layers]
????running_var?=?[torch.zeros_like(bn.running_var)?for?bn?in?bn_layers]
????ind?=?-1
????for?ind,?inputs?in?enumerate(itertools.islice(data_loader,?num_iters)):
????????with?torch.no_grad():
????????????model(inputs)
????????for?i,?bn?in?enumerate(bn_layers):
????????????#?Accumulates?the?bn?stats.
????????????running_mean[i]?+=?(bn.running_mean?-?running_mean[i])?/?(ind?+?1)
????????????running_var[i]?+=?(bn.running_var?-?running_var[i])?/?(ind?+?1)
????????????if?torch.sum(torch.isnan(bn.running_mean))?>?0?or?torch.sum(torch.isnan(bn.running_var))?>?0:
????????????????raise?RuntimeError(
????????????????????"update_bn_stats?ERROR(args.rank?{}):?Got?NaN?val".format(args.rank))
????????????if?torch.sum(torch.isinf(bn.running_mean))?>?0?or?torch.sum(torch.isinf(bn.running_var))?>?0:
????????????????raise?RuntimeError(
????????????????????"update_bn_stats?ERROR(args.rank?{}):?Got?INf?val".format(args.rank))
????????????if?torch.sum(~torch.isfinite(bn.running_mean))?>?0?or?torch.sum(~torch.isfinite(bn.running_var))?>?0:
????????????????raise?RuntimeError(
????????????????????"update_bn_stats?ERROR(args.rank?{}):?Got?INf?val".format(args.rank))
????assert?ind?==?num_iters?-?1,?(
????????"update_bn_stats?is?meant?to?run?for?{}?iterations,?"
????????"but?the?dataloader?stops?at?{}?iterations.".format(num_iters,?ind)
????)
????for?i,?bn?in?enumerate(bn_layers):
????????if?args.distributed:
????????????all_reduce(running_mean[i],?op=ReduceOp.SUM)
????????????all_reduce(running_var[i],?op=ReduceOp.SUM)
????????????running_mean[i]?=?running_mean[i]?/?args.gpu_nums
????????????running_var[i]?=?running_var[i]?/?args.gpu_nums
????????bn.running_mean?=?running_mean[i]
????????bn.running_var?=?running_var[i]
????????bn.momentum?=?momentum_actual[i]
????if?args.rank?==?0:
????????a?=?[round(i.cpu().numpy().max(),?4)?for?i?in?running_mean]
????????logger.info('bn?mean?max,?%s?(%s)',?max(a),?a)
????????a?=?[round(i.cpu().numpy().max(),?4)?for?i?in?running_var]
????????logger.info('bn?var?max,?%s?(%s)',?max(a),?a)
2.2 蒸餾
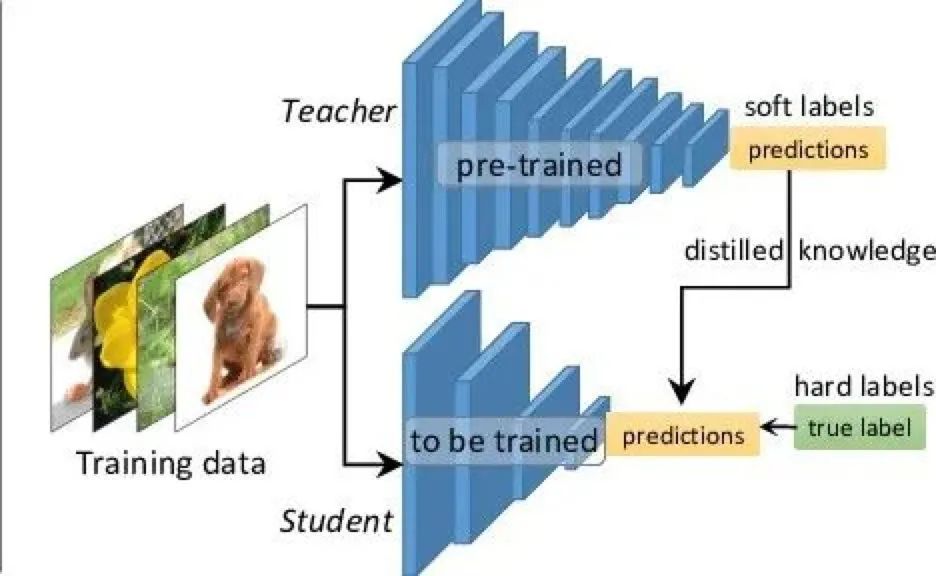
模型蒸餾是一個老生常談的話題了,不過經(jīng)過實驗以來,蒸餾的確是一個穩(wěn)定提升性能的技巧,不過這里的性能一般是指小模型來說。如果你的任務是不考慮開銷的,直接懟大模型就好了,蒸餾也不需要。但是反之,如果線上資源吃緊,要求FLOPs或者Params,那么蒸餾就是一個非常好的選擇。
舉個例子,以前每次學渣考試都是60分,學霸考試都是90分,這一次學渣通過抄襲學霸,考到了75分,學霸依然是90分,至于為什么學渣沒有考到90分,可能是因為學霸改了答案也可能是因為學霸的字寫的好。那么這個抄襲就是蒸餾,但是學霸的知識更豐富,所以分數(shù)依然很高,那這個就是所謂的模型泛華能力也叫做魯棒性。
簡而言之,蒸餾就是使得弱者逼近強者的手段。這里的弱者被叫做Student模型,強者叫做Teacher模型。
使用蒸餾最好是同源數(shù)據(jù)或者同源模型,同源數(shù)據(jù)會防止由于數(shù)據(jù)歸納的問題發(fā)生偏置,同源模型抽取信息特征近似,可以更好的用于KL散度的逼近。
蒸餾過程
先訓練一個teacher模型,可以是非常非常大的模型,只要顯存放的下就行,使用常規(guī)CrossEntropy損失進行訓練。 再訓練一個student模型,使用CrossEntropy進行訓練,同時,把訓練好的teacher模型固定參數(shù)后得到logits,用來與student模型的logits進行KL散度學習。
KL散度是一種衡量兩個分布之間的匹配程度的方法。定義如下:
其中,是近似分布,是我們想要用匹配的真實分布。如果兩個分布是完全相同的,那么KL為0,KL 散度越小,真實分布與近似分布之間的匹配就越好。
KL散度代碼如下:
class?KLSoftLoss(nn.Module):
????r"""Apply?softtarget?for?kl?loss
????Arguments:
????????reduction?(str):?"batchmean"?for?the?mean?loss?with?the?p(x)*(log(p(x))?-?log(q(x)))
????"""
????def?__init__(self,?temperature=1,?reduction="batchmean"):
????????super(KLSoftLoss,?self).__init__()
????????self.reduction?=?reduction
????????self.eps?=?1e-7
????????self.temperature?=?temperature
????????self.klloss?=?nn.KLDivLoss(reduction=self.reduction)
????def?forward(self,?s_logits,?t_logits):
????????s_prob?=?F.log_softmax(s_logits?/?self.temperature,?1)
????????t_prob?=?F.softmax(t_logits?/?self.temperature,?1)?
????????loss?=?self.klloss(s_prob,?t_prob)?*?self.temperature?*?self.temperature
????????return?loss
這里的temperature稍微控制一下分布的平滑,自己的經(jīng)驗參數(shù)是設置為5。
2.3 分辨率
一般來說,存粹的CNN網(wǎng)絡,訓練和推理的分辨率是有一定程度的關系的,這個跟我們數(shù)據(jù)增強的時候采用的resize和randomcrop也有關系。一般的時候,訓練采用先crop到256然后resize到224,大概是0.875的一個比例的關系,不管最終輸入到cnn的尺寸多大,基本上都是保持這樣的一個比例關系,resize_size = crop_size * 0.875。
那么推理的時候是否如此呢?
| train_size | crop_size | acc@top-1 |
|---|---|---|
| 224 | 224 | 82.18% |
| 224 | 256 | 82.22% |
| 224 | 320 | 82.26% |
在自己的業(yè)務數(shù)據(jù)集上實測結果如上表,可以發(fā)現(xiàn)測試的時候?qū)嶋H有0.7的倍率關系。但是如果訓練的尺寸越大,實際上測試增加分辨率帶來的提升就越小。
那么有沒有什么簡單的方法可以有效的提升推理尺寸大于訓練尺寸所帶來的收益增幅呢?
FaceBook提出了一個簡單且實用的方法FixRes,僅僅需要在正常訓練的基礎上,F(xiàn)inetune幾個epoch就可以提升精度。
 如上圖所示,雖然訓練和測試時的輸入大小相同,但是物體的分辨率明顯不同,cnn雖然可以學習到不同尺度大小的物體的特征,但是理論上測試和訓練的物體尺寸大小接近,那么效果應該是最好的。
如上圖所示,雖然訓練和測試時的輸入大小相同,但是物體的分辨率明顯不同,cnn雖然可以學習到不同尺度大小的物體的特征,但是理論上測試和訓練的物體尺寸大小接近,那么效果應該是最好的。
代碼如下:
"""
R50?為例子,這里凍結除了最后一個block的bn以及fc以外的所有參數(shù)
"""
if?args.fixres:
????#?forzen?others?layers?except?the?fc?
????for?name,?child?in?model.named_children():
????????if?'fc'?not?in?name:
????????????for?_,?params?in?child.named_parameters():
????????????????params.requires_grad?=?False?
if?args.fixres:
????model.eval()
????model.module.layer4[2].bn3.train()
#?data?aug?for?fixres?train
if?self.fix_crop:
????self.data_aug?=?imagenet_transforms.Compose(
????????[
????????????Resize(int((256?/?224)?*?self.crop_size)),
????????????imagenet_transforms.CenterCrop(self.crop_size),
????????????imagenet_transforms.ToTensor(),
????????????imagenet_transforms.Normalize(mean=self.mean,?std=self.std)
????????]
????)
訓練流程如下:
先固定除了最后一層的bn以及FC以外的所有參數(shù)。 訓練的數(shù)據(jù)增強采用推理的增強方法,crop尺寸和推理大小保持一致。 用1e-3的學習率開始進行finetune。
當然,如果想要重頭使用大尺寸進行訓練,也可以達到不錯的效果,F(xiàn)ixRes本身是為了突破這個限制,從尺寸上面進一步提升性能。
三、總結
EMA, SWA基本上都不會影響訓練的速度,還可能提點,建議打比賽大家都用起來,畢竟提升0.01都很關鍵。做業(yè)務的話可以不用太care這個東西。 precise bn, 如果數(shù)據(jù)的分布差異很大的話,最好還是使用一下,不過會影響訓練速度,可以考慮放到最后幾個epoch再使用。 蒸餾,小模型都建議使用,注意一下調(diào)參即可,也只有一個參數(shù),多試試就行了。 FixRes,固定FLOPs的場景或者想突破精度都可以使用,簡單有效。
四、參考
https://pytorch.org/blog/stochastic-weight-averaging-in-pytorch/ https://zhuanlan.zhihu.com/p/68748778 https://arxiv.org/abs/1906.06423
下一篇簡單講講數(shù)據(jù)怎么處理可以提升我們的模型的性能~
