原文鏈接：http://tecdat.cn/?p=23717

Logistic回歸，也稱為Logit模型，用于對二元結果變量進行建模。在Logit模型中，結果的對數(shù)概率被建模為預測變量的線性組合。

例子

例1. 假設我們對影響一個政治候選人是否贏得選舉的因素感興趣。結果（因）變量是二元的（0/1）；贏或輸。我們感興趣的預測變量是花在競選上的錢，花在競選上的時間，以及候選人是否是現(xiàn)任者。

例2. 一個研究者對GRE（研究生入學考試成績）、GPA（平均分）和本科院校的聲望等變量如何影響研究生院的錄取感興趣。因變量，錄取/不錄取，是一個二元變量。

數(shù)據(jù)的描述

對于我們下面的數(shù)據(jù)分析，我們將在例2的基礎上展開關于進入研究生院的分析。我們生成了假設的數(shù)據(jù)，這些數(shù)據(jù)可以在R中從我們的網(wǎng)站上獲得。請注意，R在指定文件位置時需要正斜杠（/）而不是反斜杠（），該文件在你的硬盤上。

##查看數(shù)據(jù)的前幾行
head(mydata)

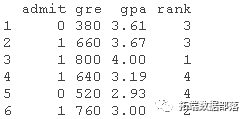
這個數(shù)據(jù)集有一個二元因（結果，因果）變量，叫做錄取。有三個預測變量：gre、gpa和rank。我們將把gre和gpa這兩個變量視為連續(xù)變量。變量rank的值為1到4。排名為1的院校有最高的聲望，而排名為4的院校有最低的聲望。我們可以通過使用總結來獲得整個數(shù)據(jù)集的基本描述。為了得到標準差，我們使用sapply對數(shù)據(jù)集中的每個變量應用sd函數(shù)。

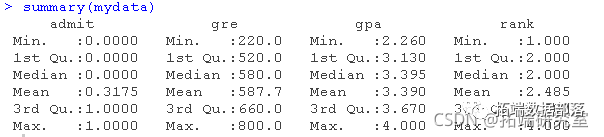
你可能考慮的分析方法

以下是你可能遇到過的一些分析方法的清單。所列的一些方法是相當合理的，而其他的方法可能有局限性。

Logistic回歸，是本文的重點。
Probit回歸。Probit分析會產(chǎn)生類似Logistic回歸的結果。選擇probit還是logit，主要取決于個人的偏好。
OLS回歸。當與二元因變量一起使用時，這個模型被稱為線性概率模型，可以作為描述條件概率的一種方式。然而，線性概率模型的誤差（即殘差）違反了OLS回歸的同方差和誤差的正態(tài)性假設，導致標準誤差和假設檢驗無效。
雙組判別函數(shù)分析。一種用于二分結果變量的多變量方法。

使用logit模型

下面的代碼使用glm（廣義線性模型）函數(shù)估計一個邏輯回歸模型。首先，我們將等級轉(zhuǎn)換為一個因子變量，以表明等級應被視為一個分類變量。

rank <- factor(rank)

由于我們給我們的模型起了個名字（mylogit），R不會從我們的回歸中產(chǎn)生任何輸出。為了得到結果，我們使用summary命令。

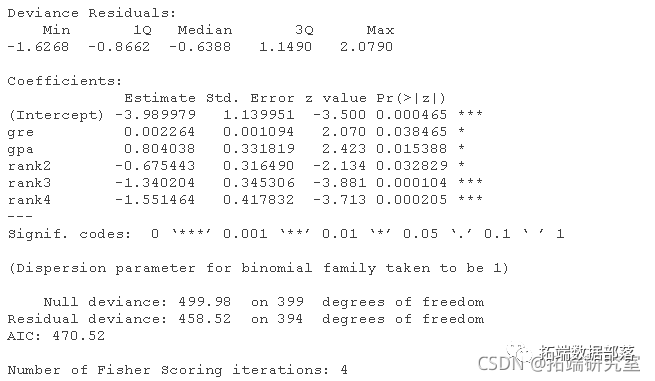
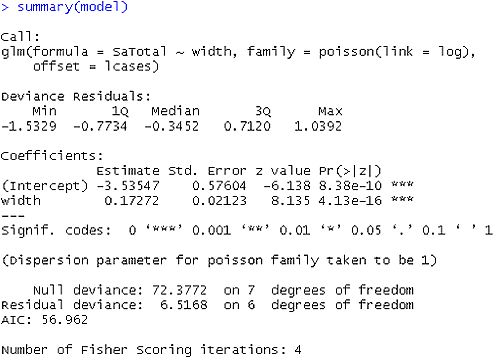
在上面的輸出中，我們首先看到的是調(diào)用，這是R提醒我們所運行的模型是什么，我們指定了哪些選項，等等。
接下來我們看到偏差殘差，這是衡量模型擬合度的一個指標。這部分輸出顯示了模型中使用的各個案例的偏差殘差的分布。下面我們討論如何使用偏差統(tǒng)計的摘要來評估模型的擬合度。
輸出的下一部分顯示了系數(shù)、它們的標準誤差、z統(tǒng)計量（有時稱為Wald z統(tǒng)計量）以及相關的p值。gre和gpa都有統(tǒng)計學意義，三個等級項也是如此。邏輯回歸系數(shù)給出了預測變量增加一個單位時結果的對數(shù)幾率變化。

gre每增加一個單位，錄取（與未錄取）的對數(shù)幾率增加0.002。
gpa增加一個單位，被研究生院錄取的對數(shù)幾率就會增加0.804。
級別的指標變量有一個稍微不同的解釋。例如，就讀于排名為2的本科院校與排名為1的院校相比，被錄取的對數(shù)幾率會改變?yōu)?0.675。
系數(shù)表下面是擬合指數(shù)，包括無效和偏差殘差以及AIC。稍后我們將展示一個例子，說明如何使用這些值來幫助評估模型的擬合。

點擊標題查閱往期內(nèi)容

R語言泊松Poisson回歸模型分析案例

左右滑動查看更多

我們可以使用confint函數(shù)來獲得系數(shù)估計值的置信區(qū)間。注意，對于logistic模型，置信區(qū)間是基于剖析的對數(shù)似然函數(shù)。我們也可以通過使用默認的方法，只根據(jù)標準誤差來獲得CI。

我們可以用wald.test函數(shù)來檢驗等級的整體效應。系數(shù)表中系數(shù)的順序與模型中項的順序相同。這一點很重要，因為wald.test函數(shù)是按照系數(shù)在模型中的順序來參考的。我們使用wald.test函數(shù)。b提供了系數(shù)，而Sigma提供了誤差項的方差協(xié)方差矩陣，最后Terms告訴R模型中哪些項要被測試，在本例中，4、5、6項是等級水平的三個項。

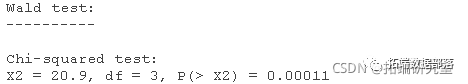
卡方檢驗統(tǒng)計量為20.9，有三個自由度，P值為0.00011，表明等級的總體影響在統(tǒng)計上是顯著的。

我們還可以檢驗關于不同等級的系數(shù)差異的其他假設。下面我們測試等級=2的系數(shù)是否等于等級=3的系數(shù)。下面的第一行代碼創(chuàng)建了一個向量l，定義了我們要執(zhí)行的測試。在這種情況下，我們要測試等級=2的項和等級=3的項（即模型中的第4和第5項）的差異（減法）。為了對比這兩個項，我們把其中一個項乘以1，另一個項乘以-1。下面的第二行代碼使用L=l來告訴R，我們希望以向量l為基礎進行測試（而不是像上面那樣使用Terms選項）。

wald.test(b , Sigma , L = l)

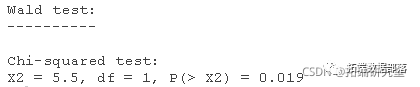
1個自由度的卡方檢驗統(tǒng)計量為5.5，P值為0.019，表明等級=2的系數(shù)和等級=3的系數(shù)之間的差異具有統(tǒng)計學意義。

你也可以對系數(shù)進行指數(shù)化，并將其解釋為概率。為了得到指數(shù)化的系數(shù)，你要告訴R你要進行指數(shù)化（exp），你要指數(shù)化的對象叫做coefficients，它是mylogit的一部分（coef(mylogit)）。我們可以使用同樣的邏輯，通過對之前的置信區(qū)間進行指數(shù)化，得到概率及其置信區(qū)間。為了把這些都放在一個表中，我們用cbind把系數(shù)和置信區(qū)間按列綁定起來。

## 概率比

##概率和95％CI

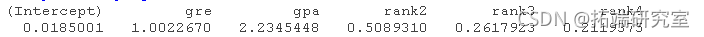
現(xiàn)在我們可以說，gpa增加一個單位，被研究生院錄取（與未被錄取）的幾率就會增加2.23倍。請注意，截距的幾率一般不會被解釋。

你也可以使用預測概率來幫助你理解模型。預測概率可以針對分類和連續(xù)預測變量進行計算。為了創(chuàng)建預測的概率，我們首先需要創(chuàng)建一個新的數(shù)據(jù)框架，其中包含我們希望自變量采取的數(shù)值，來創(chuàng)建我們的預測。

我們將首先計算每個等級值的預測錄取概率，保持gre和gpa的平均值。首先，我們創(chuàng)建并查看數(shù)據(jù)框架。

data.frame(mean(gre),  mean(gpa),  factor(1:4))

## 查看數(shù)據(jù)框

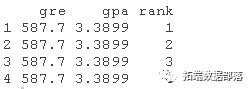
這些對象的名稱必須與上述邏輯回歸中的變量相同（例如，在本例中，gre的平均值必須被命名為gre）。現(xiàn)在我們有了要用來計算預測概率的數(shù)據(jù)框，我們可以告訴R來創(chuàng)建預測概率。下面的第一行代碼非常緊湊，我們將把它拆開來討論各個部分的作用。newdata1$rankP告訴R，我們要在數(shù)據(jù)集（數(shù)據(jù)框）newdata1中創(chuàng)建一個名為rankP的新變量，命令的其余部分告訴R，rankP的值應該是使用predict（）函數(shù)進行的預測。括號內(nèi)的選項告訴R，預測應該基于mylogit分析，預測變量的值來自newdata1，預測的類型是預測的概率（type="response"）。代碼的第二行列出數(shù)據(jù)框newdata1中的值。這是預測概率的表格。

predict(mylogit, newdata, type)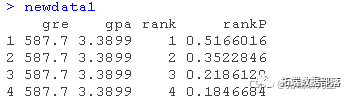

在上面的輸出中，我們看到，在保持gre和gpa的平均值的情況下，來自最高聲望的本科院校（排名=1）的學生被研究生課程錄取的預測概率為0.52，而來自排名最低的院校（排名=4）的學生為0.18。我們可以做一些非常類似的事情，創(chuàng)建一個預測概率的表格，改變gre和排名的值。我們將繪制這些圖表，因此我們將在每個等級值（即1、2、3和4）上創(chuàng)建100個200至800的gre值。

gre = rep(seq(from = 200, to = 800, length.out = 100),
    4), mean(gpa), factor(rep(1:4, each = 100))

生成預測概率的代碼（下面第一行）與之前的相同，只是我們還要提供標準誤差，這樣我們就可以繪制一個置信區(qū)間。我們在鏈接標度上得到估計值，并將預測值和置信區(qū)間都反過來轉(zhuǎn)化為概率。

    PredictedProb
    LL <- plogis(fit - (1.96 * se.fit))
    UL <- plogis(fit + (1.96 * se.fit))


##查看最終數(shù)據(jù)集的前幾行

使用預測概率的圖表來理解和/或展示模型也是有幫助的。我們將使用ggplot2軟件包來繪制圖表。下面我們用預測的概率和95%的置信區(qū)間做一個圖。

ggplot( aes(x = gre, y = Predicted))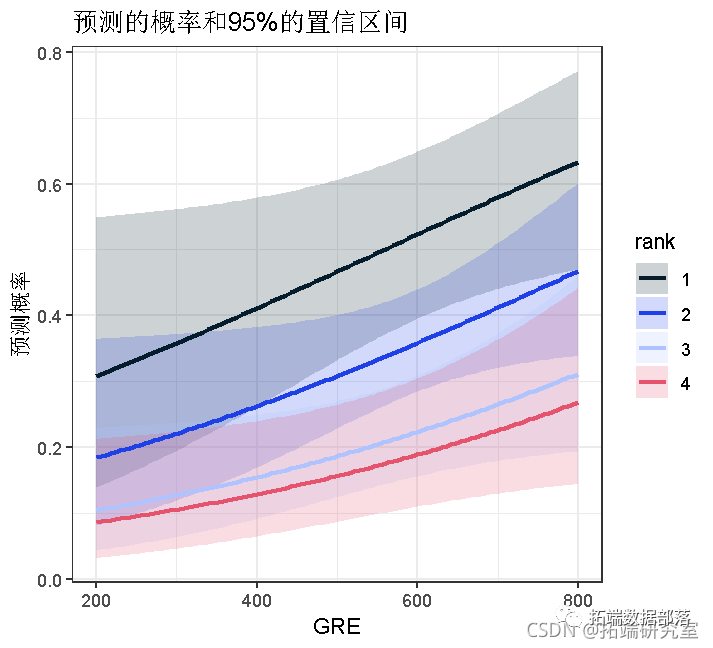

我們也可能希望看到我們的模型擬合程度的方法。在比較相互比較的模型時，這可能特別有用。summary(mylogit)產(chǎn)生的輸出包括擬合指數(shù)（顯示在系數(shù)下面），包括無效和偏差殘差以及AIC。衡量模型擬合度的一個指標是整個模型的顯著性。這個測試問的是有預測因子的模型是否比只有截距的模型（即空模型）明顯更適合。檢驗統(tǒng)計量是帶有預測因子的模型與無效模型的殘差。檢驗統(tǒng)計量是分布式的卡方，自由度等于當前模型和無效模型之間的自由度差異（即模型中預測變量的數(shù)量）。為了找到兩個模型的偏差差異（即檢驗統(tǒng)計量），我們可以使用以下命令。

with(mylogit, null.deviance - deviance)
## \[1\] 41.5

兩個模型之間差異的自由度等于模式中預測變量的數(shù)量，可以用以下方法得到。

with(mylogit, df.null - df.residual)
## \[1\] 5

最后，可以用P值得到。

## \[1\] 7.58e-08

5個自由度的卡方為41.46，相關的P值小于0.001，這告訴我們，我們的模型作為一個整體的擬合度明顯好于一個空模型。這有時被稱為似然比檢驗（偏差殘差為-2*對數(shù)似然）。要查看模型的對數(shù)似然，我們可以輸入。

logLik(mylogit)
## 'log Lik.' -229 (df=6)

需要考慮的事項

空單元格或小單元格。你應該通過分類預測因子和結果變量之間的交叉分析來檢查空單元或小單元。如果一個單元的案例很少（小單元），模型可能會變得不穩(wěn)定或根本無法運行。
樣本量。logit和probit模型都需要比OLS回歸更多的案例，因為它們使用最大似然估計技術。在只有少量案例的數(shù)據(jù)集中，有時可以用精確的Logistic回歸來估計二元結果的模型。同樣重要的是要記住，當結果是罕見的，即使整個數(shù)據(jù)集很大，也很難估計出一個Logit模型。
偽R平方。存在許多不同的偽R平方的測量方法。它們都試圖提供類似于OLS回歸中R平方所提供的信息；然而，它們都不能完全按照OLS回歸中R平方的解釋來解釋。
診斷法。邏輯回歸的診斷方法與OLS回歸的診斷方法不同，對邏輯回歸的診斷與對probit回歸的診斷相似。