「回歸分析」知識點(diǎn)梳理

↑↑↑點(diǎn)擊上方藍(lán)字，回復(fù)資料，10個G的驚喜

“正確問題的近似答案要比近似問題的精確答案更有價值”

這正是回歸分析所追求的目標(biāo)。它是最常用的預(yù)測建模技術(shù)之一，有助于在重要情況下做出更明智的決策。在本文中，我們將討論什么是回歸分析，它是如何工作的。

回歸分析是作為數(shù)據(jù)科學(xué)家需要掌握的第一個算法。它是數(shù)據(jù)分析中最常用的預(yù)測建模技術(shù)之一。即使在今天，大多數(shù)公司都使用回歸技術(shù)來實(shí)現(xiàn)大規(guī)模決策。

要回答“什么是回歸分析”這個問題，我們需要深入了解基本面。簡單的回歸分析定義是一種用于基于一個或多個獨(dú)立變量（X）預(yù)測因變量（Y）的技術(shù)。

經(jīng)典的回歸方程看起來像這樣：

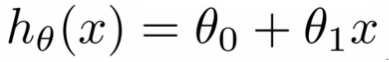
回歸方程

回歸分析源DataAspirant.com

在上面的等式中，hθ（x）是因變量Y，X是自變量，θ0是常數(shù)，并且θ1是回歸系數(shù)。

回歸分析用于在許多業(yè)務(wù)情況下做出決策。回歸分析有三個主要應(yīng)用：

由于存在許多不同的回歸分析技術(shù)，因此很難找到非常狹窄的回歸分析定義。大多數(shù)人傾向于將兩種常見的線性或邏輯回歸中的任何一種應(yīng)用于幾乎每個回歸問題。

但是，有許多可用的回歸技術(shù)，不同的技術(shù)更適合于不同的問題。回歸分析技術(shù)的類型基于：

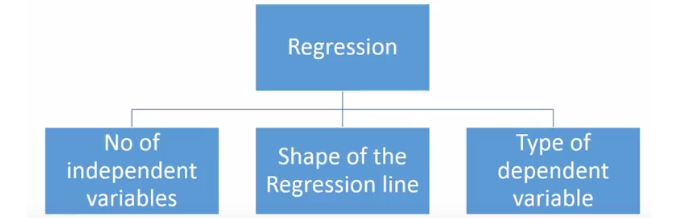回歸分析技術(shù)

1. 線性回歸

線性回歸是最常用的回歸技術(shù)。線性回歸的目的是找到一個稱為Y的連續(xù)響應(yīng)變量的方程，它將是一個或多個變量（X）的函數(shù)。

因此，線性回歸可以在僅知道X時預(yù)測Y的值。它不依賴于任何其他因素。

Y被稱為標(biāo)準(zhǔn)變量，而X被稱為預(yù)測變量。線性回歸的目的是通過點(diǎn)找到稱為回歸線的最佳擬合線。這就是數(shù)學(xué)線性回歸公式 /等式的樣子：

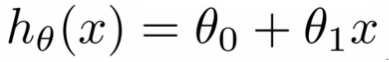
線性回歸公式

在上面的等式中，hθ（x）是標(biāo)準(zhǔn)變量Y，X是預(yù)測變量，θ0是常數(shù)，并且θ1是回歸系數(shù)

線性回歸可以進(jìn)一步分為多元回歸分析和簡單回歸分析。在簡單線性回歸中，僅使用一個獨(dú)立變量X來預(yù)測因變量Y的值。

另一方面，在多元回歸分析中，使用多個自變量來預(yù)測Y，當(dāng)然，在這兩種情況下，只有一個變量Y，唯一的區(qū)別在于自變量的數(shù)量。

例如，如果我們僅根據(jù)平方英尺來預(yù)測公寓的租金，那么這是一個簡單的線性回歸。

另一方面，如果我們根據(jù)許多因素預(yù)測租金; 平方英尺，房產(chǎn)的位置和建筑物的年齡，然后它成為多元回歸分析的一個例子。

2. Logistic回歸

要理解什么是邏輯回歸，我們必須首先理解它與線性回歸的不同之處。為了理解線性回歸和邏輯回歸之間的差異，我們需要首先理解連續(xù)變量和分類變量之間的區(qū)別。

連續(xù)變量是數(shù)值。它們在任何兩個給定值之間具有無限數(shù)量的值。示例包括視頻的長度或收到付款的時間或城市的人口。

另一方面，分類變量具有不同的組或類別。它們可能有也可能沒有邏輯順序。示例包括性別，付款方式，年齡段等。

在線性回歸中，因變量Y始終是連續(xù)變量。如果變量Y是分類變量，則不能應(yīng)用線性回歸。

如果Y是只有2個類的分類變量，則可以使用邏輯回歸來克服此問題。這些問題也稱為二元分類問題。

理解標(biāo)準(zhǔn)邏輯回歸只能用于二元分類問題也很重要。如果Y具有多于2個類，則它變?yōu)槎囝惙诸悾⑶也荒軕?yīng)用標(biāo)準(zhǔn)邏輯回歸。

邏輯回歸分析的最大優(yōu)點(diǎn)之一是它可以計(jì)算事件的預(yù)測概率分?jǐn)?shù)。這使其成為數(shù)據(jù)分析的寶貴預(yù)測建模技術(shù)。

3. 多項(xiàng)式回歸

如果自變量（X）的冪大于1，那么它被稱為多項(xiàng)式回歸。這是多項(xiàng)式回歸方程的樣子：y = a + b * x ^ 3

與線性回歸不同，最佳擬合線是直線，在多項(xiàng)式回歸中，它是適合不同數(shù)據(jù)點(diǎn)的曲線。這是多項(xiàng)式回歸方程的圖形：

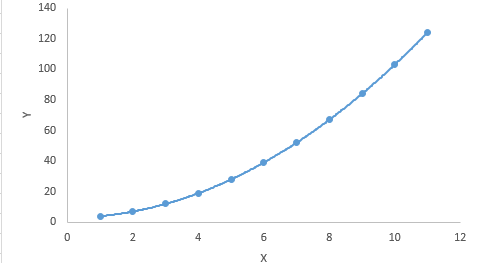
多項(xiàng)式回歸

對于多項(xiàng)式方程，人們傾向于擬合更高次多項(xiàng)式，因?yàn)樗鼘?dǎo)致更低的錯誤率。但是，這可能會導(dǎo)致過度擬合。確保曲線真正符合問題的本質(zhì)非常重要。

檢查曲線朝向兩端并確保形狀和趨勢落實(shí)到位尤為重要。多項(xiàng)式越高，它在解釋過程中產(chǎn)生奇怪結(jié)果的可能性就越大。

4. 逐步回歸

當(dāng)存在多個獨(dú)立變量時，使用逐步回歸。逐步回歸的一個特點(diǎn)是自動選擇自變量，而不涉及人的主觀性。

像R-square和t-stats這樣的統(tǒng)計(jì)值用于識別正確的自變量。當(dāng)數(shù)據(jù)集具有高維度時，通常使用逐步回歸。這是因?yàn)?span style="color: rgb(10, 203, 174);">其目標(biāo)是使用最少數(shù)量的變量最大化模型的預(yù)測能力。

逐步回歸基于預(yù)定義的條件一次增加或減少一個共變量。它一直這樣做，直到適合回歸模型。

5. 嶺回歸

當(dāng)自變量高度相關(guān)（多重共線性）時，使用嶺回歸。當(dāng)自變量高度相關(guān)時，最小二乘估計(jì)的方差非常大。

結(jié)果，觀察值與實(shí)際值有很大差異。嶺回歸通過在回歸估計(jì)中增加一定程度的偏差來解決這個問題。這是嶺回歸方程式的樣子：

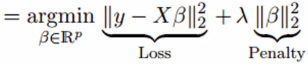
在上面的等式中，收縮參數(shù)λ（λ）用于解決多重共線性的問題。

6. 套索回歸

就像嶺回歸一樣，Lasso回歸也使用收縮參數(shù)來解決多重共線性問題。它還通過提高準(zhǔn)確性來幫助線性回歸模型。

它與嶺回歸的不同之處在于懲罰函數(shù)使用絕對值而不是正方形。這是Lasso回歸方程：

7. 彈性網(wǎng)絡(luò)回歸

ElasticNet回歸方法線性地組合了Ridge和Lasso方法的L1和L2懲罰。以下是ElasticNet回歸方程的樣子：