正文共： 8636字 8圖

預(yù)計(jì)閱讀時(shí)間： 22分鐘

一、異常檢測(cè)簡介

異常檢測(cè)是通過數(shù)據(jù)挖掘方法發(fā)現(xiàn)與數(shù)據(jù)集分布不一致的異常數(shù)據(jù)，也被稱為離群點(diǎn)、異常值檢測(cè)等等。

1.1 異常檢測(cè)適用的場景

異常檢測(cè)算法適用的場景特點(diǎn)有：（1）無標(biāo)簽或者類別極不均衡；（2）異常數(shù)據(jù)跟樣本中大多數(shù)數(shù)據(jù)的差異性較大；（3）異常數(shù)據(jù)在總體數(shù)據(jù)樣本中所占的比例很低。常見的應(yīng)用案例如：

金融領(lǐng)域：從金融數(shù)據(jù)中識(shí)別”欺詐用戶“，如識(shí)別信用卡申請(qǐng)欺詐、信用卡盜刷、信貸欺詐等；安全領(lǐng)域：判斷流量數(shù)據(jù)波動(dòng)以及是否受到攻擊等等；電商領(lǐng)域：從交易等數(shù)據(jù)中識(shí)別”惡意買家“，如羊毛黨、惡意刷屏團(tuán)伙；生態(tài)災(zāi)難預(yù)警：基于天氣指標(biāo)數(shù)據(jù)，判斷未來可能出現(xiàn)的極端天氣；醫(yī)療監(jiān)控：從醫(yī)療設(shè)備數(shù)據(jù)，發(fā)現(xiàn)可能會(huì)顯示疾病狀況的異常數(shù)據(jù)；

1.2 異常檢測(cè)存在的挑戰(zhàn)

異常檢測(cè)是熱門的研究領(lǐng)域，但由于異常存在的未知性、異質(zhì)性、特殊性及多樣性等復(fù)雜情況，整個(gè)領(lǐng)域仍有較多的挑戰(zhàn)：

• 1）最具挑戰(zhàn)性的問題之一是難以實(shí)現(xiàn)高異常檢測(cè)召回率。由于異常非常罕見且具有異質(zhì)性，因此很難識(shí)別所有異常。
• 2）異常檢測(cè)模型要提高精確度（precision）往往要深度結(jié)合業(yè)務(wù)特征，否則效果不佳，且容易導(dǎo)致對(duì)少數(shù)群體產(chǎn)生算法偏見。

二、異常檢測(cè)方法

按照訓(xùn)練集是否包含異常值可以劃分為異常值檢測(cè)（outlier detection）及新穎點(diǎn)檢測(cè)（novelty detection），新穎點(diǎn)檢測(cè)的代表方法如one class SVM。

按照異常類別的不同，異常檢測(cè)可劃分為：異常點(diǎn)檢測(cè)(如異常消費(fèi)用戶)，上下文異常檢測(cè)（如時(shí)間序列異常），組異常檢測(cè)（如異常團(tuán)伙）。

按照學(xué)習(xí)方式的不同，異常檢測(cè)可劃分為：有監(jiān)督異常檢測(cè)（Supervised Anomaly Detection）、半監(jiān)督異常檢測(cè)（Semi-Supervised Anomaly Detection）及無監(jiān)督異常檢測(cè)（Unsupervised Anomaly Detection）。現(xiàn)實(shí)情況的異常檢測(cè)問題，由于收集異常標(biāo)簽樣本的難度大，往往是沒有標(biāo)簽的，所以無監(jiān)督異常檢測(cè)應(yīng)用最為廣泛。

無監(jiān)督異常檢測(cè)按其算法思想大致可分為如下下幾類：

2.1 基于聚類的方法

基于聚類的異常檢測(cè)方法通常依賴下列假設(shè)，1）正常數(shù)據(jù)實(shí)例屬于數(shù)據(jù)中的一個(gè)簇，而異常數(shù)據(jù)實(shí)例不屬于任何簇；2）正常數(shù)據(jù)實(shí)例靠近它們最近的簇質(zhì)心，而異常數(shù)據(jù)離它們最近的簇質(zhì)心很遠(yuǎn)；3）正常數(shù)據(jù)實(shí)例屬于大而密集的簇，而異常數(shù)據(jù)實(shí)例要么屬于小簇，要么屬于稀疏簇；通過將數(shù)據(jù)歸分到不同的簇中，異常數(shù)據(jù)則是那些屬于小簇或者不屬于任何一簇或者遠(yuǎn)離簇中心的數(shù)據(jù)。

• 將距離簇中心較遠(yuǎn)的數(shù)據(jù)作為異常點(diǎn)：這類方法有 SOM、K-means、最大期望( expectation maximization，EM)及基于語義異常因子( semantic anomaly factor)算法等；

• 將聚類所得小簇?cái)?shù)據(jù)作為異常點(diǎn)：代表方法有K-means聚類；

• 將不屬于任何一簇作為異常點(diǎn)：代表方法有 DBSCAN、ROCK、SNN 聚類。

2.2 基于統(tǒng)計(jì)的方法

基于統(tǒng)計(jì)的方法依賴的假設(shè)是數(shù)據(jù)集服從某種分布( 如正態(tài)分布、泊松分布及二項(xiàng)式分布等) 或概率模型，通過判斷某數(shù)據(jù)點(diǎn)是否符合該分布/模型( 即通過小概率事件的判別) 來實(shí)現(xiàn)異常檢測(cè)。根據(jù)概率模型可分為:

• 
  
1. 參數(shù)方法，由已知分布的數(shù)據(jù)中估計(jì)模型參數(shù)( 如高斯模型) ，其中最簡單的參數(shù)異常檢測(cè)模型就是假設(shè)樣本服從一元正態(tài)分布，當(dāng)數(shù)據(jù)點(diǎn)與均值差距大于兩倍或三倍方差時(shí)，則認(rèn)為該點(diǎn)為異常;
• 
  
2. 非參數(shù)方法，在數(shù)據(jù)分布未知時(shí)，可繪制直方圖通過檢測(cè)數(shù)據(jù)是否在訓(xùn)練集所產(chǎn)生的直方圖中來進(jìn)行異常檢測(cè)。還可以利用數(shù)據(jù)的變異程度( 如均差、標(biāo)準(zhǔn)差、變異系數(shù)、四分位數(shù)間距等) 來發(fā)現(xiàn)數(shù)據(jù)中的異常點(diǎn)數(shù)據(jù)。

2.3 基于深度的方法

該方法將數(shù)據(jù)映射到 k 維空間的分層結(jié)構(gòu)中，并假設(shè)異常值分布在外圍，而正常數(shù)據(jù)點(diǎn)靠近分層結(jié)構(gòu)的中心（深度越高）。

• 半空間深度法( ISODEPTH 法) ，通過計(jì)算每個(gè)點(diǎn)的深度，并根據(jù)深度值判斷異常數(shù)據(jù)點(diǎn)。

• 最小橢球估計(jì) ( minimum volume ellipsoid estimator，MVE)法。根據(jù)大多數(shù)數(shù)據(jù)點(diǎn)( 通常為 ＞ 50% ) 的概率分布模型擬合出一個(gè)實(shí)線橢圓形所示的最小橢圓形球體的邊界，不在此邊界范圍內(nèi)的數(shù)據(jù)點(diǎn)將被判斷為異常點(diǎn)。

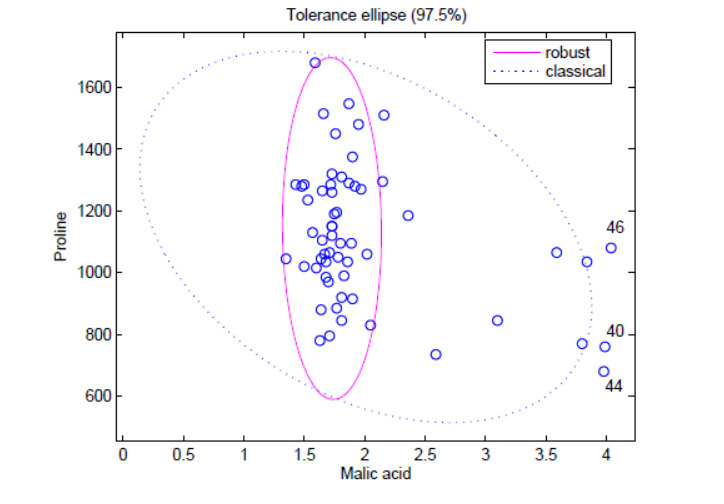
• 孤立森林。上述兩種基于深度的基礎(chǔ)模型隨著特征維度k的增加，其時(shí)間復(fù)雜性呈指數(shù)增長，通常適用于維度k≤3 時(shí)，而孤立森林通過改變計(jì)算深度的方式，也可以適用于高維的數(shù)據(jù)。

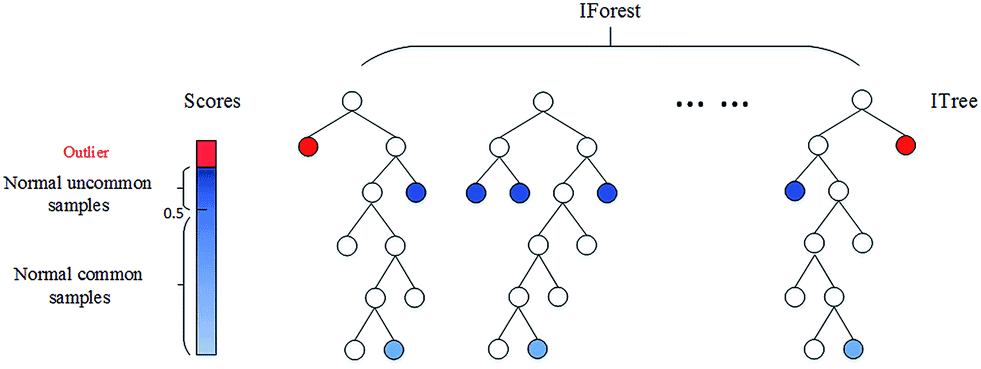
孤立森林算法是基于 Ensemble 的異常檢測(cè)方法，因此具有線性的時(shí)間復(fù)雜度。且精準(zhǔn)度較高，在處理大數(shù)據(jù)時(shí)速度快，所以目前在工業(yè)界的應(yīng)用范圍比較廣。其基本思想是：通過樹模型方法隨機(jī)地切分樣本空間，那些密度很高的簇要被切很多次才會(huì)停止切割（即每個(gè)點(diǎn)都單獨(dú)存在于一個(gè)子空間內(nèi)），但那些分布稀疏的點(diǎn)（即異常點(diǎn)），大都很早就停到一個(gè)子空間內(nèi)了。算法步驟為：1）從訓(xùn)練數(shù)據(jù)中隨機(jī)選擇 Ψ 個(gè)樣本，以此訓(xùn)練單棵樹。

2）隨機(jī)指定一個(gè)q維度（attribute），在當(dāng)前節(jié)點(diǎn)數(shù)據(jù)中隨機(jī)產(chǎn)生一個(gè)切割點(diǎn)p。p切割點(diǎn)產(chǎn)生于當(dāng)前節(jié)點(diǎn)數(shù)據(jù)中指定q維度的最大值和最小值之間。

3）在此切割點(diǎn)的選取生成了一個(gè)超平面，將當(dāng)前節(jié)點(diǎn)數(shù)據(jù)空間切分為2個(gè)子空間：把當(dāng)前所選維度下小于 p 的點(diǎn)放在當(dāng)前節(jié)點(diǎn)的左分支，把大于等于 p 的點(diǎn)放在當(dāng)前節(jié)點(diǎn)的右分支；

4）在節(jié)點(diǎn)的左分支和右分支節(jié)點(diǎn)遞歸步驟 2、3，不斷構(gòu)造新的葉子節(jié)點(diǎn)，直到葉子節(jié)點(diǎn)上只有一個(gè)數(shù)據(jù)（無法再繼續(xù)切割） 或樹已經(jīng)生長到了所設(shè)定的高度 。（設(shè)置單顆樹的最大高度是因?yàn)楫惓?shù)據(jù)記錄都比較少，其路徑長度也比較低，而我們也只需要把正常記錄和異常記錄區(qū)分開來，因此只需要關(guān)心低于平均高度的部分就好，這樣算法效率更高。）

5） 由于每顆樹訓(xùn)練的切割特征空間過程是完全隨機(jī)的，所以需要用 ensemble 的方法來使結(jié)果收斂，即多建立幾棵樹，然后綜合計(jì)算每棵樹切分結(jié)果的平均值。對(duì)于每個(gè)樣本 x，通過下面的公式計(jì)算綜合的異常得分s。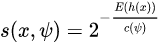h(x) 為 x 在每棵樹的高度，c(Ψ) 為給定樣本數(shù) Ψ 時(shí)路徑長度的平均值，用來對(duì)樣本 x 的路徑長度 h(x) 進(jìn)行標(biāo)準(zhǔn)化處理。

2.4 基于分類模型：

代表方法是One class SVM，其原理是尋找一個(gè)超平面將樣本中的正例圈出來，預(yù)測(cè)就是用這個(gè)超平面做決策，在圈內(nèi)的樣本就認(rèn)為是正樣本。由于核函數(shù)計(jì)算比較耗時(shí)，在海量數(shù)據(jù)的場景用的并不多。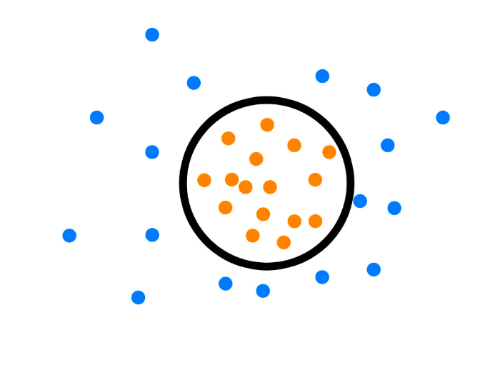

2.5 基于鄰近的方法：

依賴的假設(shè)是：正常數(shù)據(jù)實(shí)例位于密集的鄰域中，而異常數(shù)據(jù)實(shí)例附近的樣例較為稀疏。可以繼續(xù)細(xì)分為 基于密度/鄰居：

• 基于密度，該方法通過計(jì)算數(shù)據(jù)集中各數(shù)據(jù)區(qū)域的密度，將密度較低區(qū)域作為離群區(qū)域。經(jīng)典的方法為：局部離群因子( local outlier factor，LOF) 。LOF 法與傳統(tǒng)異常點(diǎn)非彼即此定義不同，將異常點(diǎn)定義局域是異常點(diǎn)，為每個(gè)數(shù)據(jù)賦值一個(gè)代表相對(duì)于其鄰域的 LOF 值，LOF 越大，說明其鄰域密度較低，越有可能是異常點(diǎn)。但在 LOF 中難以確定最小近鄰域，且隨著數(shù)據(jù)維度的升高，計(jì)算復(fù)雜度和時(shí)間復(fù)雜度增加。

• 基于距離，其基本思想是通過計(jì)算比較數(shù)據(jù)與近鄰數(shù)據(jù)集合的距離來檢測(cè)異常，正常數(shù)據(jù)點(diǎn)與其近鄰數(shù)據(jù)相似，而異常數(shù)據(jù)則有別于近鄰數(shù)據(jù)。

2.6 基于偏差的方法

當(dāng)給定一個(gè)數(shù)據(jù)集時(shí)，可通過基于偏差法找出與整個(gè)數(shù)據(jù)集特征不符的點(diǎn)，并且數(shù)據(jù)集方差會(huì)隨著異常點(diǎn)的移除而減小。該方法可分為逐個(gè)比較數(shù)據(jù)點(diǎn)的序列異常技術(shù)和 OLAP 數(shù)據(jù)立方體技術(shù)。目前該方法實(shí)際應(yīng)用較少。

2.7 基于重構(gòu)的方法

代表方法為PCA。PCA在異常檢測(cè)方面的做法，大體有兩種思路：一種是將數(shù)據(jù)映射到低維特征空間，然后在特征空間不同維度上查看每個(gè)數(shù)據(jù)點(diǎn)跟其它數(shù)據(jù)的偏差；另外一種是將數(shù)據(jù)映射到低維特征空間，然后由低維特征空間重新映射回原空間，嘗試用低維特征重構(gòu)原始數(shù)據(jù)，看重構(gòu)誤差的大小。

2.8 基于神經(jīng)網(wǎng)絡(luò)的方法：

代表方法有自動(dòng)編碼器( autoencoder，AE) ，長短期記憶神經(jīng)網(wǎng)絡(luò)（LSTM）等。

• LSTM可用于時(shí)間序列數(shù)據(jù)的異常檢測(cè)：利用歷史序列數(shù)據(jù)訓(xùn)練模型，檢測(cè)與預(yù)測(cè)值差異較大的異常點(diǎn)。
• Autoencoder異常檢測(cè) Autoencoder本質(zhì)上使用了一個(gè)神經(jīng)網(wǎng)絡(luò)來產(chǎn)生一個(gè)高維輸入的低維表示。Autoencoder與主成分分析PCA類似，但是Autoencoder在使用非線性激活函數(shù)時(shí)克服了PCA線性的限制。算法的基本上假設(shè)是異常點(diǎn)服從不同的分布。根據(jù)正常數(shù)據(jù)訓(xùn)練出來的Autoencoder，能夠?qū)⒄颖局亟ㄟ€原，但是卻無法將異于正常分布的數(shù)據(jù)點(diǎn)較好地還原，導(dǎo)致其基于重構(gòu)誤差較大。當(dāng)重構(gòu)誤差大于某個(gè)閾值時(shí)，將其標(biāo)記為異常值。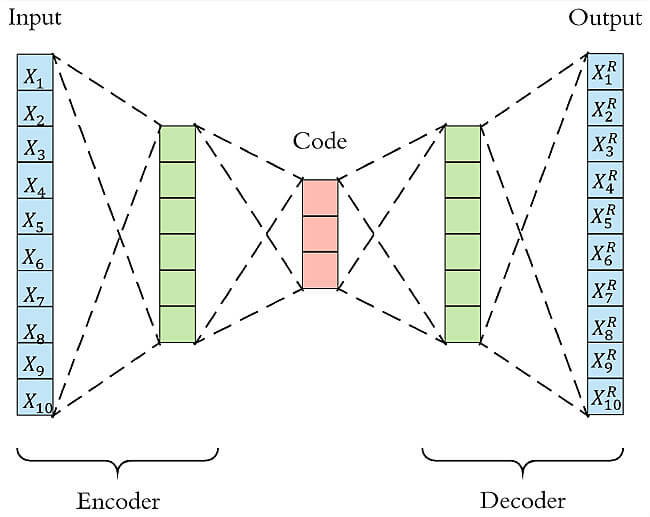

小結(jié)：無監(jiān)督異常檢測(cè)方法的要素為選擇相關(guān)的特征以及基于合理假設(shè)選擇合適的算法，可以更好的發(fā)揮異常檢測(cè)效果。

四、項(xiàng)目實(shí)戰(zhàn)：信用卡反欺詐

項(xiàng)目為kaggle上經(jīng)典的信用卡欺詐檢測(cè)，該數(shù)據(jù)集質(zhì)量高，正負(fù)樣本比例非常懸殊。我們?cè)诖隧?xiàng)目主要用了無監(jiān)督的Autoencoder新穎點(diǎn)檢測(cè)，根據(jù)重構(gòu)誤差識(shí)別異常欺詐樣本。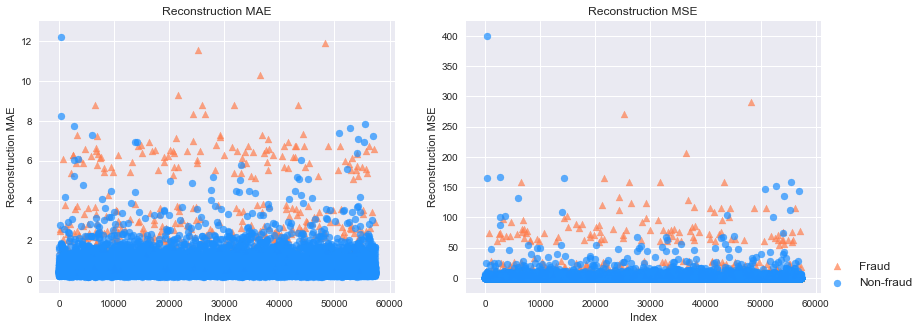

#!/usr/bin/env python
# coding: utf-8

import warnings
warnings.filterwarnings("ignore")

import pandas as pd
import numpy as np
import pickle
import matplotlib.pyplot as plt
plt.style.use('seaborn')
import tensorflow as tf
import seaborn as sns
from sklearn.model_selection import train_test_split
from keras.models import Model, load_model
from keras.layers import Input, Dense
from keras.callbacks import ModelCheckpoint
from keras import regularizers
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import roc_curve, auc, precision_recall_curve
# 安利一個(gè)異常檢測(cè)Python庫 https://github.com/yzhao062/Pyod

# 讀取數(shù)據(jù) ：信用卡欺詐數(shù)據(jù)集地址https://www.kaggle.com/mlg-ulb/creditcardfraud
d = pd.read_csv('creditcard.csv')

# 查看樣本比例
num_nonfraud = np.sum(d['Class'] == 0)
num_fraud = np.sum(d['Class'] == 1)
plt.bar(['Fraud', 'non-fraud'], [num_fraud, num_nonfraud], color='dodgerblue')
plt.show()

# 刪除時(shí)間列，對(duì)Amount進(jìn)行標(biāo)準(zhǔn)化
data = d.drop(['Time'], axis=1)
data['Amount'] = StandardScaler().fit_transform(data[['Amount']])

# 為無監(jiān)督新穎點(diǎn)檢測(cè)方法，只提取負(fù)樣本，并且按照8:2切成訓(xùn)練集和測(cè)試集
mask = (data['Class'] == 0)
X_train, X_test = train_test_split(data[mask], test_size=0.2, random_state=0)
X_train = X_train.drop(['Class'], axis=1).values
X_test = X_test.drop(['Class'], axis=1).values

# 提取所有正樣本，作為測(cè)試集的一部分
X_fraud = data[~mask].drop(['Class'], axis=1).values

# 構(gòu)建Autoencoder網(wǎng)絡(luò)模型
# 隱藏層節(jié)點(diǎn)數(shù)分別為16，8，8，16
# epoch為5，batch size為32
input_dim = X_train.shape[1]
encoding_dim = 16
num_epoch = 5
batch_size = 32

input_layer = Input(shape=(input_dim, ))
encoder = Dense(encoding_dim, activation="tanh", 
                activity_regularizer=regularizers.l1(10e-5))(input_layer)
encoder = Dense(int(encoding_dim / 2), activation="relu")(encoder)
decoder = Dense(int(encoding_dim / 2), activation='tanh')(encoder)
decoder = Dense(input_dim, activation='relu')(decoder)
autoencoder = Model(inputs=input_layer, outputs=decoder)
autoencoder.compile(optimizer='adam', 
                    loss='mean_squared_error', 
                    metrics=['mae'])

# 模型保存為model.h5，并開始訓(xùn)練模型
checkpointer = ModelCheckpoint(filepath="model.h5",
                               verbose=0,
                               save_best_only=True)
history = autoencoder.fit(X_train, X_train,
                          epochs=num_epoch,
                          batch_size=batch_size,
                          shuffle=True,
                          validation_data=(X_test, X_test),
                          verbose=1, 
                          callbacks=[checkpointer]).history


# 畫出損失函數(shù)曲線
plt.figure(figsize=(14, 5))
plt.subplot(121)
plt.plot(history['loss'], c='dodgerblue', lw=3)
plt.plot(history['val_loss'], c='coral', lw=3)
plt.title('model loss')
plt.ylabel('mse'); plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper right')

plt.subplot(122)
plt.plot(history['mae'], c='dodgerblue', lw=3)
plt.plot(history['val_mae'], c='coral', lw=3)
plt.title('model mae')
plt.ylabel('mae'); plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper right')


# 讀取模型
autoencoder = load_model('model.h5')

# 利用autoencoder重建測(cè)試集
pred_test = autoencoder.predict(X_test)
# 重建欺詐樣本
pred_fraud = autoencoder.predict(X_fraud)  

# 計(jì)算重構(gòu)MSE和MAE誤差
mse_test = np.mean(np.power(X_test - pred_test, 2), axis=1)
mse_fraud = np.mean(np.power(X_fraud - pred_fraud, 2), axis=1)
mae_test = np.mean(np.abs(X_test - pred_test), axis=1)
mae_fraud = np.mean(np.abs(X_fraud - pred_fraud), axis=1)
mse_df = pd.DataFrame()
mse_df['Class'] = [0] * len(mse_test) + [1] * len(mse_fraud)
mse_df['MSE'] = np.hstack([mse_test, mse_fraud])
mse_df['MAE'] = np.hstack([mae_test, mae_fraud])
mse_df = mse_df.sample(frac=1).reset_index(drop=True)

# 分別畫出測(cè)試集中正樣本和負(fù)樣本的還原誤差MAE和MSE
markers = ['o', '^']
markers = ['o', '^']
colors = ['dodgerblue', 'coral']
labels = ['Non-fraud', 'Fraud']

plt.figure(figsize=(14, 5))
plt.subplot(121)
for flag in [1, 0]:
    temp = mse_df[mse_df['Class'] == flag]
    plt.scatter(temp.index, 
                temp['MAE'],  
                alpha=0.7, 
                marker=markers[flag], 
                c=colors[flag], 
                label=labels[flag])
plt.title('Reconstruction MAE')
plt.ylabel('Reconstruction MAE'); plt.xlabel('Index')
plt.subplot(122)
for flag in [1, 0]:
    temp = mse_df[mse_df['Class'] == flag]
    plt.scatter(temp.index, 
                temp['MSE'],  
                alpha=0.7, 
                marker=markers[flag], 
                c=colors[flag], 
                label=labels[flag])
plt.legend(loc=[1, 0], fontsize=12); plt.title('Reconstruction MSE')
plt.ylabel('Reconstruction MSE'); plt.xlabel('Index')
plt.show()
# 下圖分別是MAE和MSE重構(gòu)誤差，其中橘黃色的點(diǎn)是信用欺詐，也就是異常點(diǎn)；藍(lán)色是正常點(diǎn)。我們可以看出異常點(diǎn)的重構(gòu)誤差整體很高。

# 畫出Precision-Recall曲線
plt.figure(figsize=(14, 6))
for i, metric in enumerate(['MAE', 'MSE']):
    plt.subplot(1, 2, i+1)
    precision, recall, _ = precision_recall_curve(mse_df['Class'], mse_df[metric])
    pr_auc = auc(recall, precision)
    plt.title('Precision-Recall curve based on %s\nAUC = %0.2f'%(metric, pr_auc))
    plt.plot(recall[:-2], precision[:-2], c='coral', lw=4)
    plt.xlabel('Recall'); plt.ylabel('Precision')
plt.show()

# 畫出ROC曲線
plt.figure(figsize=(14, 6))
for i, metric in enumerate(['MAE', 'MSE']):
    plt.subplot(1, 2, i+1)
    fpr, tpr, _ = roc_curve(mse_df['Class'], mse_df[metric])
    roc_auc = auc(fpr, tpr)
    plt.title('Receiver Operating Characteristic based on %s\nAUC = %0.2f'%(metric, roc_auc))
    plt.plot(fpr, tpr, c='coral', lw=4)
    plt.plot([0,1],[0,1], c='dodgerblue', ls='--')
    plt.ylabel('TPR'); plt.xlabel('FPR')
plt.show()
# 不管是用MAE還是MSE作為劃分標(biāo)準(zhǔn)，模型的表現(xiàn)都算是很好的。PR AUC分別是0.51和0.44，而ROC AUC都達(dá)到了0.95。

# 畫出MSE、MAE散點(diǎn)圖
markers = ['o', '^']
colors = ['dodgerblue', 'coral']
labels = ['Non-fraud', 'Fraud']

plt.figure(figsize=(10, 5))
for flag in [1, 0]:
    temp = mse_df[mse_df['Class'] == flag]
    plt.scatter(temp['MAE'], 
                temp['MSE'],  
                alpha=0.7, 
                marker=markers[flag], 
                c=colors[flag], 
                label=labels[flag])
plt.legend(loc=[1, 0])
plt.ylabel('Reconstruction RMSE'); plt.xlabel('Reconstruction MAE')
plt.show()

文章首發(fā)于算法進(jìn)階，公眾號(hào)閱讀原文可訪問GitHub項(xiàng)目源碼