異常檢測算法速覽（Python代碼）
點擊下方卡片，關(guān)注“新機器視覺”公眾號
視覺/圖像重磅干貨，第一時間送達
正文共： 8636字 8圖
預計閱讀時間： 22分鐘
一、異常檢測簡介
異常檢測是通過數(shù)據(jù)挖掘方法發(fā)現(xiàn)與數(shù)據(jù)集分布不一致的異常數(shù)據(jù)，也被稱為離群點、異常值檢測等等。
1.1 異常檢測適用的場景
異常檢測算法適用的場景特點有：（1）無標簽或者類別極不均衡；（2）異常數(shù)據(jù)跟樣本中大多數(shù)數(shù)據(jù)的差異性較大；（3）異常數(shù)據(jù)在總體數(shù)據(jù)樣本中所占的比例很低。常見的應用案例如：
金融領(lǐng)域：從金融數(shù)據(jù)中識別”欺詐用戶“，如識別信用卡申請欺詐、信用卡盜刷、信貸欺詐等；安全領(lǐng)域：判斷流量數(shù)據(jù)波動以及是否受到攻擊等等；電商領(lǐng)域：從交易等數(shù)據(jù)中識別”惡意買家“，如羊毛黨、惡意刷屏團伙；生態(tài)災難預警：基于天氣指標數(shù)據(jù)，判斷未來可能出現(xiàn)的極端天氣；醫(yī)療監(jiān)控：從醫(yī)療設備數(shù)據(jù)，發(fā)現(xiàn)可能會顯示疾病狀況的異常數(shù)據(jù)；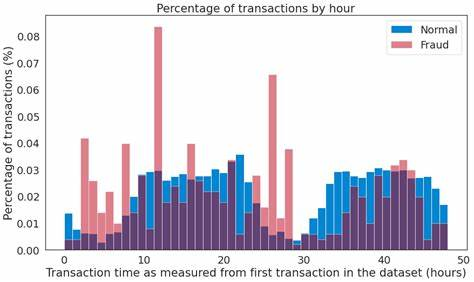
1.2 異常檢測存在的挑戰(zhàn)
異常檢測是熱門的研究領(lǐng)域，但由于異常存在的未知性、異質(zhì)性、特殊性及多樣性等復雜情況，整個領(lǐng)域仍有較多的挑戰(zhàn)：
1）最具挑戰(zhàn)性的問題之一是難以實現(xiàn)高異常檢測召回率。由于異常非常罕見且具有異質(zhì)性，因此很難識別所有異常。 2）異常檢測模型要提高精確度（precision）往往要深度結(jié)合業(yè)務特征，否則效果不佳，且容易導致對少數(shù)群體產(chǎn)生算法偏見。
二、異常檢測方法
按照訓練集是否包含異常值可以劃分為異常值檢測（outlier detection）及新穎點檢測（novelty detection），新穎點檢測的代表方法如one class SVM。
按照異常類別的不同，異常檢測可劃分為：異常點檢測(如異常消費用戶)，上下文異常檢測（如時間序列異常），組異常檢測（如異常團伙）。
按照學習方式的不同，異常檢測可劃分為：有監(jiān)督異常檢測（Supervised Anomaly Detection）、半監(jiān)督異常檢測（Semi-Supervised Anomaly Detection）及無監(jiān)督異常檢測（Unsupervised Anomaly Detection）。現(xiàn)實情況的異常檢測問題，由于收集異常標簽樣本的難度大，往往是沒有標簽的，所以無監(jiān)督異常檢測應用最為廣泛。
無監(jiān)督異常檢測按其算法思想大致可分為如下下幾類：
2.1 基于聚類的方法
基于聚類的異常檢測方法通常依賴下列假設，1）正常數(shù)據(jù)實例屬于數(shù)據(jù)中的一個簇，而異常數(shù)據(jù)實例不屬于任何簇；2）正常數(shù)據(jù)實例靠近它們最近的簇質(zhì)心，而異常數(shù)據(jù)離它們最近的簇質(zhì)心很遠；3）正常數(shù)據(jù)實例屬于大而密集的簇，而異常數(shù)據(jù)實例要么屬于小簇，要么屬于稀疏簇；通過將數(shù)據(jù)歸分到不同的簇中，異常數(shù)據(jù)則是那些屬于小簇或者不屬于任何一簇或者遠離簇中心的數(shù)據(jù)。
將距離簇中心較遠的數(shù)據(jù)作為異常點：這類方法有 SOM、K-means、最大期望( expectation maximization，EM)及基于語義異常因子( semantic anomaly factor)算法等；
將聚類所得小簇數(shù)據(jù)作為異常點：代表方法有K-means聚類；
將不屬于任何一簇作為異常點：代表方法有 DBSCAN、ROCK、SNN 聚類。
2.2 基于統(tǒng)計的方法
基于統(tǒng)計的方法依賴的假設是數(shù)據(jù)集服從某種分布( 如正態(tài)分布、泊松分布及二項式分布等) 或概率模型，通過判斷某數(shù)據(jù)點是否符合該分布/模型( 即通過小概率事件的判別) 來實現(xiàn)異常檢測。根據(jù)概率模型可分為:
參數(shù)方法，由已知分布的數(shù)據(jù)中估計模型參數(shù)( 如高斯模型) ，其中最簡單的參數(shù)異常檢測模型就是假設樣本服從一元正態(tài)分布，當數(shù)據(jù)點與均值差距大于兩倍或三倍方差時，則認為該點為異常; 非參數(shù)方法，在數(shù)據(jù)分布未知時，可繪制直方圖通過檢測數(shù)據(jù)是否在訓練集所產(chǎn)生的直方圖中來進行異常檢測。還可以利用數(shù)據(jù)的變異程度( 如均差、標準差、變異系數(shù)、四分位數(shù)間距等) 來發(fā)現(xiàn)數(shù)據(jù)中的異常點數(shù)據(jù)。
2.3 基于深度的方法
該方法將數(shù)據(jù)映射到 k 維空間的分層結(jié)構(gòu)中，并假設異常值分布在外圍，而正常數(shù)據(jù)點靠近分層結(jié)構(gòu)的中心（深度越高）。
半空間深度法( ISODEPTH 法) ，通過計算每個點的深度，并根據(jù)深度值判斷異常數(shù)據(jù)點。
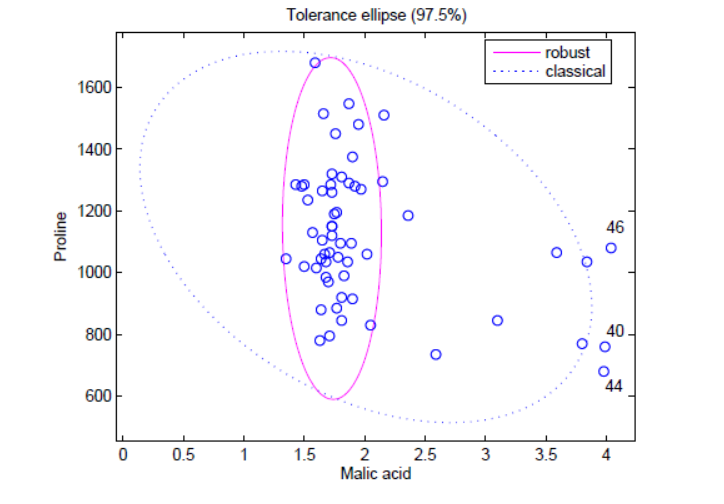
最小橢球估計 ( minimum volume ellipsoid estimator，MVE)法。根據(jù)大多數(shù)數(shù)據(jù)點( 通常為 ＞ 50% ) 的概率分布模型擬合出一個實線橢圓形所示的最小橢圓形球體的邊界，不在此邊界范圍內(nèi)的數(shù)據(jù)點將被判斷為異常點。
孤立森林。上述兩種基于深度的基礎(chǔ)模型隨著特征維度k的增加，其時間復雜性呈指數(shù)增長，通常適用于維度k≤3 時，而孤立森林通過改變計算深度的方式，也可以適用于高維的數(shù)據(jù)。
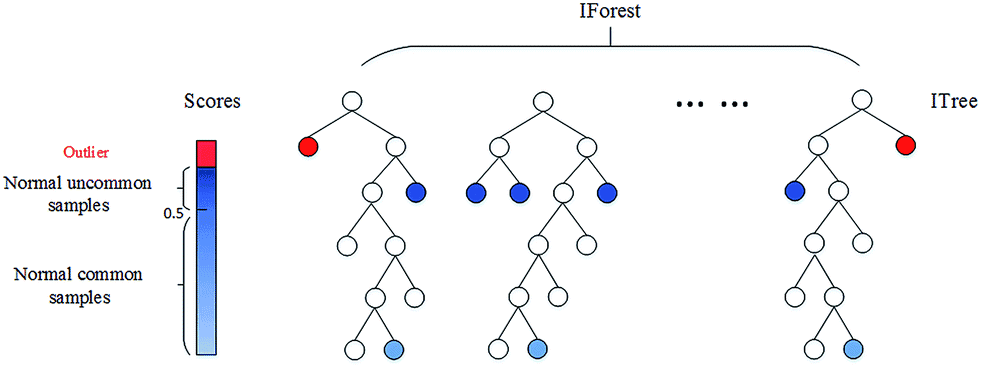
孤立森林算法是基于 Ensemble 的異常檢測方法，因此具有線性的時間復雜度。且精準度較高，在處理大數(shù)據(jù)時速度快，所以目前在工業(yè)界的應用范圍比較廣。其基本思想是：通過樹模型方法隨機地切分樣本空間，那些密度很高的簇要被切很多次才會停止切割（即每個點都單獨存在于一個子空間內(nèi)），但那些分布稀疏的點（即異常點），大都很早就停到一個子空間內(nèi)了。算法步驟為：1）從訓練數(shù)據(jù)中隨機選擇 Ψ 個樣本，以此訓練單棵樹。
2）隨機指定一個q維度（attribute），在當前節(jié)點數(shù)據(jù)中隨機產(chǎn)生一個切割點p。p切割點產(chǎn)生于當前節(jié)點數(shù)據(jù)中指定q維度的最大值和最小值之間。
3）在此切割點的選取生成了一個超平面，將當前節(jié)點數(shù)據(jù)空間切分為2個子空間：把當前所選維度下小于 p 的點放在當前節(jié)點的左分支，把大于等于 p 的點放在當前節(jié)點的右分支；
4）在節(jié)點的左分支和右分支節(jié)點遞歸步驟 2、3，不斷構(gòu)造新的葉子節(jié)點，直到葉子節(jié)點上只有一個數(shù)據(jù)（無法再繼續(xù)切割） 或樹已經(jīng)生長到了所設定的高度 。（設置單顆樹的最大高度是因為異常數(shù)據(jù)記錄都比較少，其路徑長度也比較低，而我們也只需要把正常記錄和異常記錄區(qū)分開來，因此只需要關(guān)心低于平均高度的部分就好，這樣算法效率更高。）
5） 由于每顆樹訓練的切割特征空間過程是完全隨機的，所以需要用 ensemble 的方法來使結(jié)果收斂，即多建立幾棵樹，然后綜合計算每棵樹切分結(jié)果的平均值。對于每個樣本 x，通過下面的公式計算綜合的異常得分s。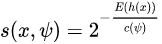
h(x) 為 x 在每棵樹的高度，c(Ψ) 為給定樣本數(shù) Ψ 時路徑長度的平均值，用來對樣本 x 的路徑長度 h(x) 進行標準化處理。
2.4 基于分類模型：
代表方法是One class SVM，其原理是尋找一個超平面將樣本中的正例圈出來，預測就是用這個超平面做決策，在圈內(nèi)的樣本就認為是正樣本。由于核函數(shù)計算比較耗時，在海量數(shù)據(jù)的場景用的并不多。
2.5 基于鄰近的方法：
依賴的假設是：正常數(shù)據(jù)實例位于密集的鄰域中，而異常數(shù)據(jù)實例附近的樣例較為稀疏。可以繼續(xù)細分為 基于密度/鄰居：
基于密度，該方法通過計算數(shù)據(jù)集中各數(shù)據(jù)區(qū)域的密度，將密度較低區(qū)域作為離群區(qū)域。經(jīng)典的方法為：局部離群因子( local outlier factor，LOF) 。LOF 法與傳統(tǒng)異常點非彼即此定義不同，將異常點定義局域是異常點，為每個數(shù)據(jù)賦值一個代表相對于其鄰域的 LOF 值，LOF 越大，說明其鄰域密度較低，越有可能是異常點。但在 LOF 中難以確定最小近鄰域，且隨著數(shù)據(jù)維度的升高，計算復雜度和時間復雜度增加。
基于距離，其基本思想是通過計算比較數(shù)據(jù)與近鄰數(shù)據(jù)集合的距離來檢測異常，正常數(shù)據(jù)點與其近鄰數(shù)據(jù)相似，而異常數(shù)據(jù)則有別于近鄰數(shù)據(jù)。
2.6 基于偏差的方法
當給定一個數(shù)據(jù)集時，可通過基于偏差法找出與整個數(shù)據(jù)集特征不符的點，并且數(shù)據(jù)集方差會隨著異常點的移除而減小。該方法可分為逐個比較數(shù)據(jù)點的序列異常技術(shù)和 OLAP 數(shù)據(jù)立方體技術(shù)。目前該方法實際應用較少。
2.7 基于重構(gòu)的方法
代表方法為PCA。PCA在異常檢測方面的做法，大體有兩種思路：一種是將數(shù)據(jù)映射到低維特征空間，然后在特征空間不同維度上查看每個數(shù)據(jù)點跟其它數(shù)據(jù)的偏差；另外一種是將數(shù)據(jù)映射到低維特征空間，然后由低維特征空間重新映射回原空間，嘗試用低維特征重構(gòu)原始數(shù)據(jù)，看重構(gòu)誤差的大小。
2.8 基于神經(jīng)網(wǎng)絡的方法：
代表方法有自動編碼器( autoencoder，AE) ，長短期記憶神經(jīng)網(wǎng)絡（LSTM）等。
LSTM可用于時間序列數(shù)據(jù)的異常檢測：利用歷史序列數(shù)據(jù)訓練模型，檢測與預測值差異較大的異常點。 Autoencoder異常檢測 Autoencoder本質(zhì)上使用了一個神經(jīng)網(wǎng)絡來產(chǎn)生一個高維輸入的低維表示。Autoencoder與主成分分析PCA類似，但是Autoencoder在使用非線性激活函數(shù)時克服了PCA線性的限制。算法的基本上假設是異常點服從不同的分布。根據(jù)正常數(shù)據(jù)訓練出來的Autoencoder，能夠?qū)⒄颖局亟ㄟ€原，但是卻無法將異于正常分布的數(shù)據(jù)點較好地還原，導致其基于重構(gòu)誤差較大。當重構(gòu)誤差大于某個閾值時，將其標記為異常值。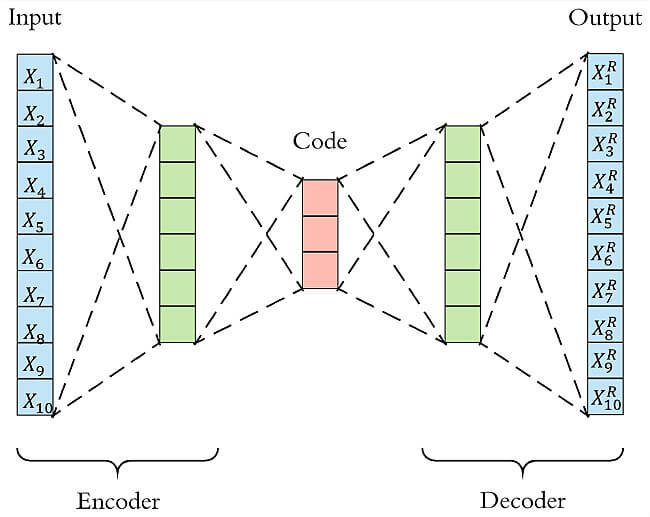 
小結(jié)：無監(jiān)督異常檢測方法的要素為選擇相關(guān)的特征以及基于合理假設選擇合適的算法，可以更好的發(fā)揮異常檢測效果。
四、項目實戰(zhàn)：信用卡反欺詐
項目為kaggle上經(jīng)典的信用卡欺詐檢測，該數(shù)據(jù)集質(zhì)量高，正負樣本比例非常懸殊。我們在此項目主要用了無監(jiān)督的Autoencoder新穎點檢測，根據(jù)重構(gòu)誤差識別異常欺詐樣本。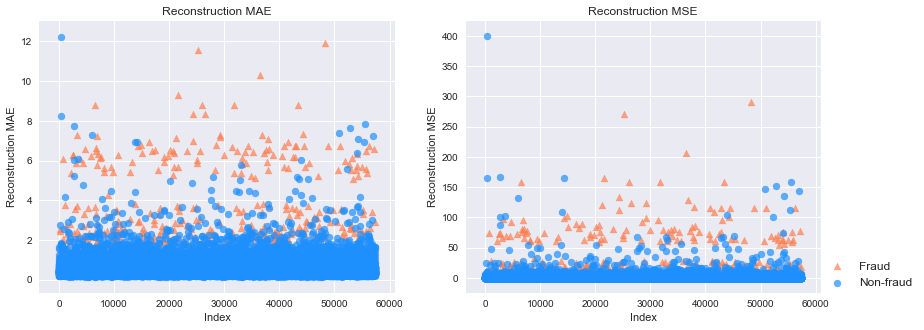
#!/usr/bin/env python
# coding: utf-8
import warnings
warnings.filterwarnings("ignore")
import pandas as pd
import numpy as np
import pickle
import matplotlib.pyplot as plt
plt.style.use('seaborn')
import tensorflow as tf
import seaborn as sns
from sklearn.model_selection import train_test_split
from keras.models import Model, load_model
from keras.layers import Input, Dense
from keras.callbacks import ModelCheckpoint
from keras import regularizers
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import roc_curve, auc, precision_recall_curve
# 安利一個異常檢測Python庫 https://github.com/yzhao062/Pyod
# 讀取數(shù)據(jù) ：信用卡欺詐數(shù)據(jù)集地址https://www.kaggle.com/mlg-ulb/creditcardfraud
d = pd.read_csv('creditcard.csv')
# 查看樣本比例
num_nonfraud = np.sum(d['Class'] == 0)
num_fraud = np.sum(d['Class'] == 1)
plt.bar(['Fraud', 'non-fraud'], [num_fraud, num_nonfraud], color='dodgerblue')
plt.show()
# 刪除時間列，對Amount進行標準化
data = d.drop(['Time'], axis=1)
data['Amount'] = StandardScaler().fit_transform(data[['Amount']])
# 為無監(jiān)督新穎點檢測方法，只提取負樣本，并且按照8:2切成訓練集和測試集
mask = (data['Class'] == 0)
X_train, X_test = train_test_split(data[mask], test_size=0.2, random_state=0)
X_train = X_train.drop(['Class'], axis=1).values
X_test = X_test.drop(['Class'], axis=1).values
# 提取所有正樣本，作為測試集的一部分
X_fraud = data[~mask].drop(['Class'], axis=1).values
# 構(gòu)建Autoencoder網(wǎng)絡模型
# 隱藏層節(jié)點數(shù)分別為16，8，8，16
# epoch為5，batch size為32
input_dim = X_train.shape[1]
encoding_dim = 16
num_epoch = 5
batch_size = 32
input_layer = Input(shape=(input_dim, ))
encoder = Dense(encoding_dim, activation="tanh",
activity_regularizer=regularizers.l1(10e-5))(input_layer)
encoder = Dense(int(encoding_dim / 2), activation="relu")(encoder)
decoder = Dense(int(encoding_dim / 2), activation='tanh')(encoder)
decoder = Dense(input_dim, activation='relu')(decoder)
autoencoder = Model(inputs=input_layer, outputs=decoder)
autoencoder.compile(optimizer='adam',
loss='mean_squared_error',
metrics=['mae'])
# 模型保存為model.h5，并開始訓練模型
checkpointer = ModelCheckpoint(filepath="model.h5",
verbose=0,
save_best_only=True)
history = autoencoder.fit(X_train, X_train,
epochs=num_epoch,
batch_size=batch_size,
shuffle=True,
validation_data=(X_test, X_test),
verbose=1,
callbacks=[checkpointer]).history
# 畫出損失函數(shù)曲線
plt.figure(figsize=(14, 5))
plt.subplot(121)
plt.plot(history['loss'], c='dodgerblue', lw=3)
plt.plot(history['val_loss'], c='coral', lw=3)
plt.title('model loss')
plt.ylabel('mse'); plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper right')
plt.subplot(122)
plt.plot(history['mae'], c='dodgerblue', lw=3)
plt.plot(history['val_mae'], c='coral', lw=3)
plt.title('model mae')
plt.ylabel('mae'); plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper right')
# 讀取模型
autoencoder = load_model('model.h5')
# 利用autoencoder重建測試集
pred_test = autoencoder.predict(X_test)
# 重建欺詐樣本
pred_fraud = autoencoder.predict(X_fraud)
# 計算重構(gòu)MSE和MAE誤差
mse_test = np.mean(np.power(X_test - pred_test, 2), axis=1)
mse_fraud = np.mean(np.power(X_fraud - pred_fraud, 2), axis=1)
mae_test = np.mean(np.abs(X_test - pred_test), axis=1)
mae_fraud = np.mean(np.abs(X_fraud - pred_fraud), axis=1)
mse_df = pd.DataFrame()
mse_df['Class'] = [0] * len(mse_test) + [1] * len(mse_fraud)
mse_df['MSE'] = np.hstack([mse_test, mse_fraud])
mse_df['MAE'] = np.hstack([mae_test, mae_fraud])
mse_df = mse_df.sample(frac=1).reset_index(drop=True)
# 分別畫出測試集中正樣本和負樣本的還原誤差MAE和MSE
markers = ['o', '^']
markers = ['o', '^']
colors = ['dodgerblue', 'coral']
labels = ['Non-fraud', 'Fraud']
plt.figure(figsize=(14, 5))
plt.subplot(121)
for flag in [1, 0]:
temp = mse_df[mse_df['Class'] == flag]
plt.scatter(temp.index,
temp['MAE'],
alpha=0.7,
marker=markers[flag],
c=colors[flag],
label=labels[flag])
plt.title('Reconstruction MAE')
plt.ylabel('Reconstruction MAE'); plt.xlabel('Index')
plt.subplot(122)
for flag in [1, 0]:
temp = mse_df[mse_df['Class'] == flag]
plt.scatter(temp.index,
temp['MSE'],
alpha=0.7,
marker=markers[flag],
c=colors[flag],
label=labels[flag])
plt.legend(loc=[1, 0], fontsize=12); plt.title('Reconstruction MSE')
plt.ylabel('Reconstruction MSE'); plt.xlabel('Index')
plt.show()
# 下圖分別是MAE和MSE重構(gòu)誤差，其中橘黃色的點是信用欺詐，也就是異常點；藍色是正常點。我們可以看出異常點的重構(gòu)誤差整體很高。
# 畫出Precision-Recall曲線
plt.figure(figsize=(14, 6))
for i, metric in enumerate(['MAE', 'MSE']):
plt.subplot(1, 2, i+1)
precision, recall, _ = precision_recall_curve(mse_df['Class'], mse_df[metric])
pr_auc = auc(recall, precision)
plt.title('Precision-Recall curve based on %s\nAUC = %0.2f'%(metric, pr_auc))
plt.plot(recall[:-2], precision[:-2], c='coral', lw=4)
plt.xlabel('Recall'); plt.ylabel('Precision')
plt.show()
# 畫出ROC曲線
plt.figure(figsize=(14, 6))
for i, metric in enumerate(['MAE', 'MSE']):
plt.subplot(1, 2, i+1)
fpr, tpr, _ = roc_curve(mse_df['Class'], mse_df[metric])
roc_auc = auc(fpr, tpr)
plt.title('Receiver Operating Characteristic based on %s\nAUC = %0.2f'%(metric, roc_auc))
plt.plot(fpr, tpr, c='coral', lw=4)
plt.plot([0,1],[0,1], c='dodgerblue', ls='--')
plt.ylabel('TPR'); plt.xlabel('FPR')
plt.show()
# 不管是用MAE還是MSE作為劃分標準，模型的表現(xiàn)都算是很好的。PR AUC分別是0.51和0.44，而ROC AUC都達到了0.95。
# 畫出MSE、MAE散點圖
markers = ['o', '^']
colors = ['dodgerblue', 'coral']
labels = ['Non-fraud', 'Fraud']
plt.figure(figsize=(10, 5))
for flag in [1, 0]:
temp = mse_df[mse_df['Class'] == flag]
plt.scatter(temp['MAE'],
temp['MSE'],
alpha=0.7,
marker=markers[flag],
c=colors[flag],
label=labels[flag])
plt.legend(loc=[1, 0])
plt.ylabel('Reconstruction RMSE'); plt.xlabel('Reconstruction MAE')
plt.show()
—版權(quán)聲明—
僅用于學術(shù)分享，版權(quán)屬于原作者。
若有侵權(quán)，請聯(lián)系微信號:yiyang-sy 刪除或修改！