PyTorch 源碼解讀之 torch.autograd

前言

本篇筆記以介紹 pytorch 中的 autograd 模塊功能為主，主要涉及 torch/autograd 下代碼，不涉及底層的 C++ 實(shí)現(xiàn)。本文涉及的源碼以 PyTorch 1.7 為準(zhǔn)。

• torch.autograd.function （函數(shù)的反向傳播）
• torch.autograd.functional （計(jì)算圖的反向傳播）
• torch.autograd.gradcheck （數(shù)值梯度檢查）
• torch.autograd.anomaly_mode （在自動(dòng)求導(dǎo)時(shí)檢測(cè)錯(cuò)誤產(chǎn)生路徑）
• torch.autograd.grad_mode （設(shè)置是否需要梯度）
• model.eval() 與 torch.no_grad()
• torch.autograd.profiler （提供 function 級(jí)別的統(tǒng)計(jì)信息）

torch.autograd.function （函數(shù)的反向傳播）

我們?cè)跇?gòu)建網(wǎng)絡(luò)的時(shí)候，通常使用 pytorch 所提供的nn.Module （例如nn.Conv2d, nn.ReLU等）作為基本單元。而這些 Module 通常是包裹 autograd function，以其作為真正實(shí)現(xiàn)的部分。例如nn.ReLU實(shí)際使用torch.nn.functional.relu（F.relu）:

from?torch.nn?import?functional?as?F

class?ReLU(Module):
????__constants__?=?['inplace']
????inplace:?bool

????def?__init__(self,?inplace:?bool?=?False):
????????super(ReLU,?self).__init__()
????????self.inplace?=?inplace

????def?forward(self,?input:?Tensor)?->?Tensor:
????????return?F.relu(input,?inplace=self.inplace)

這里的F.relu類型為function，若再剝開(kāi)一層，其實(shí)際包裹的函數(shù)類型為builtin_function_or_method，這也是真正完成運(yùn)算的部分。這些部分通常使用 C++ 實(shí)現(xiàn)（如ATen）。至此我們知道，一個(gè)模型的運(yùn)算部分由 autograd functions 組成，這些 autograd functions 內(nèi)部定義了 forward，backward 用以描述前向和梯度反傳的過(guò)程，組合后可以實(shí)現(xiàn)整個(gè)模型的前向和梯度反傳。以torch.autograd.function中所定義的Function類為基類，我們可以實(shí)現(xiàn)自定義的autograd function，所實(shí)現(xiàn)的 function 需包含forward及backward兩個(gè)方法。以下以Exp和GradCoeff兩個(gè)自定義 autograd function 為例進(jìn)行講解：

class?Exp(Function):????????????????????#?此層計(jì)算e^x
????
????@staticmethod
????def?forward(ctx,?i):????????????????#?模型前向
????????result?=?i.exp()
????????ctx.save_for_backward(result)???#?保存所需內(nèi)容，以備backward時(shí)使用，所需的結(jié)果會(huì)被保存在saved_tensors元組中；此處僅能保存tensor類型變量，若其余類型變量（Int等），可直接賦予ctx作為成員變量，也可以達(dá)到保存效果
????????return?result
????
????@staticmethod
????def?backward(ctx,?grad_output):?????#?模型梯度反傳
????????result,?=?ctx.saved_tensors?????#?取出forward中保存的result
????????return?grad_output?*?result?????#?計(jì)算梯度并返回

#?嘗試使用
x?=?torch.tensor([1.],?requires_grad=True)??#?需要設(shè)置tensor的requires_grad屬性為T(mén)rue，才會(huì)進(jìn)行梯度反傳
ret?=?Exp.apply(x)??????????????????????????#?使用apply方法調(diào)用自定義autograd?function
print(ret)??????????????????????????????????#?tensor([2.7183],?grad_fn=)
ret.backward()??????????????????????????????#?反傳梯度
print(x.grad)???????????????????????????????#?tensor([2.7183])

Exp 函數(shù)的前向很簡(jiǎn)單，直接調(diào)用 tensor 的成員方法exp即可。反向時(shí)，我們知道 , 因此我們直接使用 乘以grad_output即得梯度。我們發(fā)現(xiàn)，我們自定義的函數(shù)Exp正確地進(jìn)行了前向與反向。同時(shí)我們還注意到，前向后所得的結(jié)果包含了grad_fn屬性，這一屬性指向用于計(jì)算其梯度的函數(shù)（即Exp的backward函數(shù)）。關(guān)于這點(diǎn)，在接下來(lái)的部分會(huì)有更詳細(xì)的說(shuō)明。接下來(lái)我們看另一個(gè)函數(shù)GradCoeff，其功能是反傳梯度時(shí)乘以一個(gè)自定義系數(shù)。

????class?GradCoeff(Function):???????
???????????
????????@staticmethod
????????def?forward(ctx,?x,?coeff):?????????????????#?模型前向
????????????ctx.coeff?=?coeff???????????????????????#?將coeff存為ctx的成員變量
????????????return?x.view_as(x)

????????@staticmethod
????????def?backward(ctx,?grad_output):?????????????#?模型梯度反傳
????????????return?ctx.coeff?*?grad_output,?None????#?backward的輸出個(gè)數(shù)，應(yīng)與forward的輸入個(gè)數(shù)相同，此處coeff不需要梯度，因此返回None
????
????#?嘗試使用
????x?=?torch.tensor([2.],?requires_grad=True)
????ret?=?GradCoeff.apply(x,?-0.1)??????????????????#?前向需要同時(shí)提供x及coeff，設(shè)置coeff為-0.1
????ret?=?ret?**?2??????????????????????????
????print(ret)??????????????????????????????????????#?tensor([4.],?grad_fn=)
????ret.backward()??
????print(x.grad)???????????????????????????????????#?tensor([-0.4000])，梯度已乘以相應(yīng)系數(shù)

torch.autograd.functional （計(jì)算圖的反向傳播）

在此前一節(jié)，我們描述了單個(gè)函數(shù)的反向傳播，以及如何編寫(xiě)定制的 autograd function。在這一節(jié)中，我們簡(jiǎn)單介紹 pytorch 中所提供的計(jì)算圖反向傳播的接口。

在訓(xùn)練過(guò)程中，我們通常利用 prediction 和 groundtruth label 來(lái)計(jì)算 loss（loss 的類型為T(mén)ensor），隨后調(diào)用loss.backward()進(jìn)行梯度反傳。而 Tensor 類的backward方法，實(shí)際調(diào)用的就是torch.autograd.backward這一接口。這一 python 接口實(shí)現(xiàn)了計(jì)算圖級(jí)的反向傳播。

??class?Tensor(torch._C._TensorBase)?
????def?backward(self,?gradient=None,?retain_graph=None,?create_graph=False):
????????relevant_args?=?(self,)
????????...
????????torch.autograd.backward(self,?gradient,?retain_graph,?create_graph)
????????#?gradient:?形狀與tensor一致，可以理解為鏈?zhǔn)角髮?dǎo)的中間結(jié)果，若tensor標(biāo)量，可以省略（默認(rèn)為1）
????????#?retain_graph:?多次反向傳播時(shí)梯度累加。反向傳播的中間緩存會(huì)被清空，為進(jìn)行多次反向傳播需指定retain_graph=True來(lái)保存這些緩存。
????????#?create_graph:?為反向傳播的過(guò)程同樣建立計(jì)算圖，可用于計(jì)算二階導(dǎo)

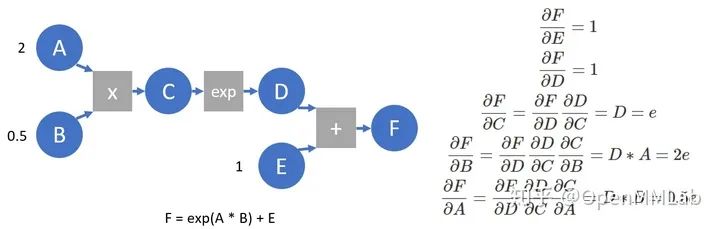
在 pytorch 實(shí)現(xiàn)中，autograd 會(huì)隨著用戶的操作，記錄生成當(dāng)前 variable 的所有操作，并建立一個(gè)有向無(wú)環(huán)圖 (DAG)。圖中記錄了操作Function，每一個(gè)變量在圖中的位置可通過(guò)其grad_fn屬性在圖中的位置推測(cè)得到。在反向傳播過(guò)程中，autograd 沿著這個(gè)圖從當(dāng)前變量（根節(jié)點(diǎn) F）溯源，可以利用鏈?zhǔn)角髮?dǎo)法則計(jì)算所有葉子節(jié)點(diǎn)的梯度。每一個(gè)前向傳播操作的函數(shù)都有與之對(duì)應(yīng)的反向傳播函數(shù)用來(lái)計(jì)算輸入的各個(gè) variable 的梯度，這些函數(shù)的函數(shù)名通常以Backward結(jié)尾。我們構(gòu)建一個(gè)簡(jiǎn)化的計(jì)算圖，并以此為例進(jìn)行簡(jiǎn)單介紹。

????A?=?torch.tensor(2.,?requires_grad=True)
????B?=?torch.tensor(.5,?requires_grad=True)
????E?=?torch.tensor(1.,?requires_grad=True)
????C?=?A?*?B
????D?=?C.exp()
????F?=?D?+?E
????print(F)????????#?tensor(3.7183,?grad_fn=)?打印計(jì)算結(jié)果，可以看到F的grad_fn指向AddBackward，即產(chǎn)生F的運(yùn)算
????print([x.is_leaf?for?x?in?[A,?B,?C,?D,?E,?F]])??#?[True,?True,?False,?False,?True,?False]?打印是否為葉節(jié)點(diǎn)，由用戶創(chuàng)建，且requires_grad設(shè)為T(mén)rue的節(jié)點(diǎn)為葉節(jié)點(diǎn)
????print([x.grad_fn?for?x?in?[F,?D,?C,?A]])????#?[,?,?,?None]??每個(gè)變量的grad_fn指向產(chǎn)生其算子的backward?function，葉節(jié)點(diǎn)的grad_fn為空
????print(F.grad_fn.next_functions)?#?((,?0),?(,?0))?由于F?=?D?+?E，?因此F.grad_fn.next_functions也存在兩項(xiàng)，分別對(duì)應(yīng)于D,?E兩個(gè)變量，每個(gè)元組中的第一項(xiàng)對(duì)應(yīng)于相應(yīng)變量的grad_fn，第二項(xiàng)指示相應(yīng)變量是產(chǎn)生其op的第幾個(gè)輸出。E作為葉節(jié)點(diǎn)，其上沒(méi)有g(shù)rad_fn，但有梯度累積函數(shù)，即AccumulateGrad（由于反傳時(shí)多出可能產(chǎn)生梯度，需要進(jìn)行累加）
????F.backward(retain_graph=True)???#?進(jìn)行梯度反傳
????print(A.grad,?B.grad,?E.grad)???#?tensor(1.3591)?tensor(5.4366)?tensor(1.)?算得每個(gè)變量梯度，與求導(dǎo)得到的相符
????print(C.grad,?D.grad)???#?None?None?為節(jié)約空間，梯度反傳完成后，中間節(jié)點(diǎn)的梯度并不會(huì)保留

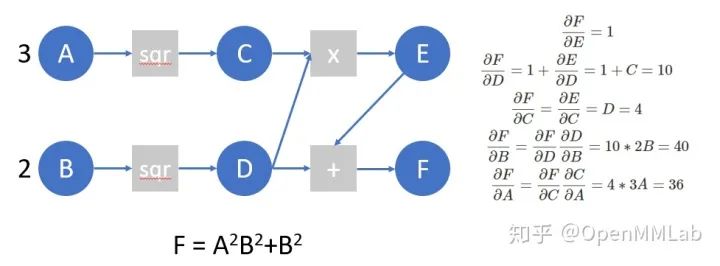
我們?cè)賮?lái)看下面的計(jì)算圖，并在這個(gè)計(jì)算圖上模擬 autograd 所做的工作：

????A?=?torch.tensor([3.],?requires_grad=True)
????B?=?torch.tensor([2.],?requires_grad=True)
????C?=?A?**?2
????D?=?B?**?2
????E?=?C?*?D
????F?=?D?+?E
????
????F.manual_grad?=?torch.tensor(1)?????????????????????????????#?我們用manual_grad表示，在已知計(jì)算圖結(jié)構(gòu)的情況下，我們模擬autograd過(guò)程手動(dòng)算得的梯度
????D.manual_grad,?E.manual_grad?=?F.grad_fn(F.manual_grad)?????
????C.manual_grad,?tmp2?=?E.grad_fn(E.manual_grad)
????D.manual_grad?=?D.manual_grad?+?tmp2????????????????????????#?這里我們先完成D上的梯度累加，再進(jìn)行反傳
????A.manual_grad?=?C.grad_fn(C.manual_grad)
????B.manual_grad?=?D.grad_fn(D.manual_grad)????????????????????#?(tensor([24.],?grad_fn=),?tensor([40.],?grad_fn=))

下面，我們編寫(xiě)一個(gè)簡(jiǎn)單的函數(shù)，在這個(gè)計(jì)算圖上進(jìn)行autograd，并驗(yàn)證結(jié)果是否正確：

# 這一例子僅可用于每個(gè)op只產(chǎn)生一個(gè)輸出的情況，且效率很低（由于對(duì)于某一節(jié)點(diǎn)，每次未等待所有梯度反傳至此節(jié)點(diǎn)，就直接將本次反傳回的梯度直接反傳至葉節(jié)點(diǎn)）

def?autograd(grad_fn,?gradient):
????????auto_grad?=?{}
????????queue?=?[[grad_fn,?gradient]]
????????while?queue?!=?[]:
????????????item?=?queue.pop()
????????????gradients?=?item[0](item[1])
????????????functions?=?[x[0]?for?x?in?item[0].next_functions]????
????????????if?type(gradients)?is?not?tuple:
????????????????gradients?=?(gradients,?)
????????????for?grad,?func?in?zip(gradients,?functions):????
????????????????if?type(func).__name__?==?'AccumulateGrad':
????????????????????if?hasattr(func.variable,?'auto_grad'):
????????????????????????func.variable.auto_grad?=?func.variable.auto_grad?+?grad
????????????????????else:
????????????????????????func.variable.auto_grad?=?grad
????????????????else:
????????????????????queue.append([func,?grad])
????
????A?=?torch.tensor([3.],?requires_grad=True)
????B?=?torch.tensor([2.],?requires_grad=True)
????C?=?A?**?2
????D?=?B?**?2
????E?=?C?*?D
????F?=?D?+?E
????
????autograd(F.grad_fn,?torch.tensor(1))
????print(A.auto_grad,?B.auto_grad)?????????#?tensor(24.,?grad_fn=)?tensor(40.,?grad_fn=)
????
????#?這一autograd同樣可作用于編寫(xiě)的模型，我們將會(huì)看到，它與pytorch自帶的backward產(chǎn)生了同樣的結(jié)果
????from?torch?import?nn
????
????class?MLP(nn.Module):
????????def?__init__(self):
????????????super().__init__()
????????????self.fc1?=?nn.Linear(10,?5)
????????????self.relu?=?nn.ReLU()
????????????self.fc2?=?nn.Linear(5,?2)
????????????self.fc3?=?nn.Linear(5,?2)
????????????self.fc4?=?nn.Linear(2,?2)
????
????????def?forward(self,?x):
????????????x?=?self.fc1(x)
????????????x?=?self.relu(x)
????????????x1?=?self.fc2(x)
????????????x2?=?self.fc3(x)
????????????x2?=?self.relu(x2)
????????????x2?=?self.fc4(x2)
????????????return?x1?+?x2
????
????x?=?torch.ones([10],?requires_grad=True)
????mlp?=?MLP()
????mlp_state_dict?=?mlp.state_dict()
????
????#?自定義autograd
????mlp?=?MLP()
????mlp.load_state_dict(mlp_state_dict)
????y?=?mlp(x)
????z?=?torch.sum(y)
????autograd(z.grad_fn,?torch.tensor(1.))
????print(x.auto_grad)?#?tensor([-0.0121,??0.0055,?-0.0756,?-0.0747,??0.0134,??0.0867,?-0.0546,??0.1121,?-0.0934,?-0.1046],?grad_fn=)
????
????mlp?=?MLP()
????mlp.load_state_dict(mlp_state_dict)
????y?=?mlp(x)
????z?=?torch.sum(y)
????z.backward()
????print(x.grad)?#?tensor([-0.0121,??0.0055,?-0.0756,?-0.0747,??0.0134,??0.0867,?-0.0546,??0.1121,?-0.0934,?-0.1046])

pytorch 使用動(dòng)態(tài)圖，它的計(jì)算圖在每次前向傳播時(shí)都是從頭開(kāi)始構(gòu)建，所以它能夠使用python 控制語(yǔ)句（如 for、if 等）根據(jù)需求創(chuàng)建計(jì)算圖。下面提供一個(gè)例子：

????def?f(x):
????????result?=?1
????????for?ii?in?x:
????????????if?ii.item()>0:?result=ii*result
????????return?result
????
????x?=?torch.tensor([0.3071,??1.1043,??1.3605,?-0.3471],?requires_grad=True)
????y?=?f(x)????#?y?=?x[0]*x[1]*x[2]
????y.backward()
????print(x.grad)???#?tensor([1.5023,?0.4178,?0.3391,?0.0000])
????
????x?=?torch.tensor([?1.2817,??1.7840,?-1.7033,??0.1302],?requires_grad=True)
????y?=?f(x)????#?y?=?x[0]*x[1]*x[3]
????y.backward()
????print(x.grad)???#?tensor([0.2323,?0.1669,?0.0000,?2.2866])

此前的例子使用的是Tensor.backward()接口（內(nèi)部調(diào)用autograd.backward），下面我們來(lái)介紹autograd提供的jacobian()和hessian()接口，并直接利用其進(jìn)行自動(dòng)微分。這兩個(gè)函數(shù)的輸入為運(yùn)算函數(shù)（接受輸入 tensor，返回輸出 tensor）和輸入 tensor，返回 jacobian 和 hessian 矩陣。對(duì)于jacobian接口，輸入輸出均可以為 n 維張量，對(duì)于hessian接口，輸出必需為一標(biāo)量。jacobian返回的張量 shape 為output_dim x input_dim（若函數(shù)輸出為標(biāo)量，則 output_dim 可省略），hessian返回的張量為input_dim x input_dim。除此之外，這兩個(gè)自動(dòng)微分接口同時(shí)支持運(yùn)算函數(shù)接收和輸出多個(gè) tensor。

????from?torch.autograd.functional?import?jacobian,?hessian
????from?torch.nn?import?Linear,?AvgPool2d
????
????fc?=?Linear(4,?2)
????pool?=?AvgPool2d(kernel_size=2)
????
????def?scalar_func(x):
????????y?=?x?**?2
????????z?=?torch.sum(y)
????????return?z
????
????def?vector_func(x):
????????y?=?fc(x)
????????return?y
????
????def?mat_func(x):
????????x?=?x.reshape((1,?1,)?+?x.shape)
????????x?=?pool(x)
????????x?=?x.reshape(x.shape[2:])
????????return?x?**?2
????
????vector_input?=?torch.randn(4,?requires_grad=True)
????mat_input?=?torch.randn((4,?4),?requires_grad=True)
????
????j?=?jacobian(scalar_func,?vector_input)
????assert?j.shape?==?(4,?)
????assert?torch.all(jacobian(scalar_func,?vector_input)?==?2?*?vector_input)
????h?=?hessian(scalar_func,?vector_input)
????assert?h.shape?==?(4,?4)
????assert?torch.all(hessian(scalar_func,?vector_input)?==?2?*?torch.eye(4))
????j?=?jacobian(vector_func,?vector_input)
????assert?j.shape?==?(2,?4)
????assert?torch.all(j?==?fc.weight)
????j?=?jacobian(mat_func,?mat_input)
????assert?j.shape?==?(2,?2,?4,?4)

在此前的例子中，我們已經(jīng)介紹了，autograd.backward()為節(jié)約空間，僅會(huì)保存葉節(jié)點(diǎn)的梯度。若我們想得知輸出關(guān)于某一中間結(jié)果的梯度，我們可以選擇使用autograd.grad()接口，或是使用hook機(jī)制：

????A?=?torch.tensor(2.,?requires_grad=True)
????B?=?torch.tensor(.5,?requires_grad=True)
????C?=?A?*?B
????D?=?C.exp()
????torch.autograd.grad(D,?(C,?A))??#?(tensor(2.7183),?tensor(1.3591)),?返回的梯度為tuple類型,?grad接口支持對(duì)多個(gè)變量計(jì)算梯度
????
????def?variable_hook(grad):????????????????????????#?hook注冊(cè)在Tensor上，輸入為反傳至這一tensor的梯度
????????print('the?gradient?of?C?is：',?grad)
????
????A?=?torch.tensor(2.,?requires_grad=True)
????B?=?torch.tensor(.5,?requires_grad=True)
????C?=?A?*?B
????hook_handle?=?C.register_hook(variable_hook)????#?在中間變量C上注冊(cè)hook
????D?=?C.exp()?????????????????
????D.backward()????????????????????????????????????#?反傳時(shí)打印：the?gradient?of?C?is：?tensor(2.7183)
????hook_handle.remove()????????????????????????????#?如不再需要，可remove掉這一hook

torch.autograd.gradcheck （數(shù)值梯度檢查）

在編寫(xiě)好自己的 autograd function 后，可以利用gradcheck中提供的gradcheck和gradgradcheck接口，對(duì)數(shù)值算得的梯度和求導(dǎo)算得的梯度進(jìn)行比較，以檢查backward是否編寫(xiě)正確。以函數(shù)為例，數(shù)值法求得 點(diǎn)的梯度為：。 在下面的例子中，我們自己實(shí)現(xiàn)了Sigmoid函數(shù)，并利用gradcheck來(lái)檢查backward的編寫(xiě)是否正確。

????class?Sigmoid(Function):
????????????????????????????????????????????????????
????????@staticmethod
????????def?forward(ctx,?x):?
????????????output?=?1?/?(1?+?torch.exp(-x))
????????????ctx.save_for_backward(output)
????????????return?output
????
????????@staticmethod
????????def?backward(ctx,?grad_output):?
????????????output,??=?ctx.saved_tensors
????????????grad_x?=?output?*?(1?-?output)?*?grad_output
????????????return?grad_x
????
????test_input?=?torch.randn(4,?requires_grad=True)?????#?tensor([-0.4646,?-0.4403,??1.2525,?-0.5953],?requires_grad=True)
????torch.autograd.gradcheck(Sigmoid.apply,?(test_input,),?eps=1e-3)????#?pass
????torch.autograd.gradcheck(torch.sigmoid,?(test_input,),?eps=1e-3)????#?pass
????torch.autograd.gradcheck(Sigmoid.apply,?(test_input,),?eps=1e-4)????#?fail
????torch.autograd.gradcheck(torch.sigmoid,?(test_input,),?eps=1e-4)????#?fail

我們發(fā)現(xiàn)：eps 為 1e-3 時(shí)，我們編寫(xiě)的 Sigmoid 和 torch 自帶的 builtin Sigmoid 都可以通過(guò)梯度檢查，但 eps 下降至 1e-4 時(shí)，兩者反而都無(wú)法通過(guò)。而一般直覺(jué)下，計(jì)算數(shù)值梯度時(shí)， eps 越小，求得的值應(yīng)該更接近于真實(shí)的梯度。這里的反常現(xiàn)象，是由于機(jī)器精度帶來(lái)的誤差所致：test_input的類型為torch.float32，因此在 eps 過(guò)小的情況下，產(chǎn)生了較大的精度誤差（計(jì)算數(shù)值梯度時(shí)，eps 作為被除數(shù)），因而與真實(shí)精度間產(chǎn)生了較大的 gap。將test_input換為float64的 tensor 后，不再出現(xiàn)這一現(xiàn)象。這點(diǎn)同時(shí)提醒我們，在編寫(xiě)backward時(shí)，要考慮的數(shù)值計(jì)算的一些性質(zhì)，盡可能保留更精確的結(jié)果。

test_input?=?torch.randn(4,?requires_grad=True,?dtype=torch.float64)????#?tensor([-0.4646,?-0.4403,??1.2525,?-0.5953],?dtype=torch.float64,?requires_grad=True)
????torch.autograd.gradcheck(Sigmoid.apply,?(test_input,),?eps=1e-4)????#?pass
????torch.autograd.gradcheck(torch.sigmoid,?(test_input,),?eps=1e-4)????#?pass
????
????torch.autograd.gradcheck(Sigmoid.apply,?(test_input,),?eps=1e-6)????#?pass
????torch.autograd.gradcheck(torch.sigmoid,?(test_input,),?eps=1e-6)????#?pass

torch.autograd.anomaly_mode （在自動(dòng)求導(dǎo)時(shí)檢測(cè)錯(cuò)誤產(chǎn)生路徑）

可用于在自動(dòng)求導(dǎo)時(shí)檢測(cè)錯(cuò)誤產(chǎn)生路徑，借助with autograd.detect_anomaly(): 或是torch.autograd.set_detect_anomaly(True)來(lái)啟用：

????>>>?import?torch
????>>>?from?torch?import?autograd
????>>>
????>>>?class?MyFunc(autograd.Function):
????...
????...?????@staticmethod
????...?????def?forward(ctx,?inp):
????...?????????return?inp.clone()
????...
????...?????@staticmethod
????...?????def?backward(ctx,?gO):
????...?????????#?Error?during?the?backward?pass
????...?????????raise?RuntimeError("Some?error?in?backward")
????...?????????return?gO.clone()
????>>>
????>>>?def?run_fn(a):
????...?????out?=?MyFunc.apply(a)
????...?????return?out.sum()
????>>>
????>>>?inp?=?torch.rand(10,?10,?requires_grad=True)
????>>>?out?=?run_fn(inp)
????>>>?out.backward()
????????Traceback?(most?recent?call?last):
??????????Some?Error?Log
????????RuntimeError:?Some?error?in?backward
????>>>?with?autograd.detect_anomaly():
????...?????inp?=?torch.rand(10,?10,?requires_grad=True)
????...?????out?=?run_fn(inp)
????...?????out.backward()
????????Traceback?of?forward?call?that?caused?the?error:????????????#?檢測(cè)到錯(cuò)誤發(fā)生的Trace
??????????File?"tmp.py",?line?53,?in?
????????????out?=?run_fn(inp)
??????????File?"tmp.py",?line?44,?in?run_fn
????????????out?=?MyFunc.apply(a)
????????Traceback?(most?recent?call?last):
??????????Some?Error?Log
????????RuntimeError:?Some?error?in?backward

torch.autograd.grad_mode （設(shè)置是否需要梯度）

我們?cè)?inference 的過(guò)程中，不希望 autograd 對(duì) tensor 求導(dǎo)，因?yàn)榍髮?dǎo)需要緩存許多中間結(jié)構(gòu)，增加額外的內(nèi)存/顯存開(kāi)銷(xiāo)。在 inference 時(shí)，關(guān)閉自動(dòng)求導(dǎo)可實(shí)現(xiàn)一定程度的速度提升，并節(jié)省大量?jī)?nèi)存及顯存（被節(jié)省的不僅限于原先用于梯度存儲(chǔ)的部分）。我們可以利用grad_mode中的troch.no_grad()來(lái)關(guān)閉自動(dòng)求導(dǎo)：

????from?torchvision.models?import?resnet50
????import?torch
????
????net?=?resnet50().cuda(0)
????num?=?128
????inp?=?torch.ones([num,?3,?224,?224]).cuda(0)
????net(inp)????????????????????????????????????????#?若不開(kāi)torch.no_grad()，batch_size為128時(shí)就會(huì)OOM?(在1080?Ti上)
????
????net?=?resnet50().cuda(1)
????num?=?512
????inp?=?torch.ones([num,?3,?224,?224]).cuda(1)????
????with?torch.no_grad():???????????????????????????#?打開(kāi)torch.no_grad()后，batch_size為512時(shí)依然能跑inference?(節(jié)約超過(guò)4倍顯存)
????????net(inp)

model.eval()與torch.no_grad()

這兩項(xiàng)實(shí)際無(wú)關(guān)，在 inference 的過(guò)程中需要都打開(kāi)：model.eval()令 model 中的BatchNorm, Dropout等 module 采用 eval mode，保證 inference 結(jié)果的正確性，但不起到節(jié)省顯存的作用；torch.no_grad()聲明不計(jì)算梯度，節(jié)省大量?jī)?nèi)存和顯存。

torch.autograd.profiler （提供function級(jí)別的統(tǒng)計(jì)信息）

????import?torch
????from?torchvision.models?import?resnet18
????
????x?=?torch.randn((1,?3,?224,?224),?requires_grad=True)
????model?=?resnet18()
????with?torch.autograd.profiler.profile()?as?prof:
????????for?_?in?range(100):
????????????y?=?model(x)
????????????y?=?torch.sum(y)
????????????y.backward()
????#?NOTE:?some?columns?were?removed?for?brevity
????print(prof.key_averages().table(sort_by="self_cpu_time_total"))

輸出為包含 CPU 時(shí)間及占比，調(diào)用次數(shù)等信息（由于一個(gè) kernel 可能還會(huì)調(diào)用其他 kernel，因此 Self CPU 指他本身所耗時(shí)間（不含其他 kernel 被調(diào)用所耗時(shí)間））：

????---------------------------------------------??------------??------------??------------??------------??------------??------------??
?????????????????????????????????????????????Name????Self?CPU?%??????Self?CPU???CPU?total?%?????CPU?total??CPU?time?avg????#?of?Calls??
????---------------------------------------------??------------??------------??------------??------------??------------??------------??
??????????aten::mkldnn_convolution_backward_input????????18.69%????????1.722s????????18.88%????????1.740s?????870.001us??????????2000??
?????????????????????????aten::mkldnn_convolution????????17.07%????????1.573s????????17.28%????????1.593s?????796.539us??????????2000??
????????aten::mkldnn_convolution_backward_weights????????16.96%????????1.563s????????17.21%????????1.586s?????792.996us??????????2000??
??????????????????????????aten::native_batch_norm?????????9.51%?????876.994ms????????15.06%????????1.388s?????694.049us??????????2000??
????????????????????aten::max_pool2d_with_indices?????????9.47%?????872.695ms?????????9.48%?????873.802ms???????8.738ms???????????100??
?????????????????????????????????????aten::select?????????7.00%?????645.298ms????????10.06%?????926.831ms???????7.356us????????126000??
?????????????????aten::native_batch_norm_backward?????????6.67%?????614.718ms????????12.16%????????1.121s?????560.466us??????????2000??
?????????????????????????????????aten::as_strided?????????3.07%?????282.885ms?????????3.07%?????282.885ms???????2.229us????????126900??
???????????????????????????????????????aten::add_?????????2.85%?????262.832ms?????????2.85%?????262.832ms??????37.350us??????????7037??
??????????????????????????????????????aten::empty?????????1.23%?????113.274ms?????????1.23%?????113.274ms???????4.089us?????????27700??
?????????????????????????aten::threshold_backward?????????1.10%?????101.094ms?????????1.17%?????107.383ms??????63.166us??????????1700??
????????????????????????????????????????aten::add?????????0.88%??????81.476ms?????????0.99%??????91.350ms??????32.625us??????????2800??
???????????aten::max_pool2d_with_indices_backward?????????0.86%??????79.174ms?????????1.02%??????93.706ms?????937.064us???????????100??
?????????????????????????????????aten::threshold_?????????0.56%??????51.678ms?????????0.56%??????51.678ms??????30.399us??????????1700??
??????????????????torch::autograd::AccumulateGrad?????????0.40%??????36.909ms?????????2.81%?????258.754ms??????41.072us??????????6300??
?????????????????????????????????aten::empty_like?????????0.35%??????32.532ms?????????0.63%??????57.630ms???????6.861us??????????8400??
??????????????????????????NativeBatchNormBackward?????????0.32%??????29.572ms????????12.48%????????1.151s?????575.252us??????????2000??
???????????????????????????????aten::_convolution?????????0.31%??????28.182ms????????17.63%????????1.625s?????812.258us??????????2000??
?????????????????????????????????????????aten::mm?????????0.27%??????24.983ms?????????0.32%??????29.522ms?????147.611us???????????200??
?????????????????????????????????????aten::stride?????????0.27%??????24.665ms?????????0.27%??????24.665ms???????0.583us?????????42300??
????????????????aten::mkldnn_convolution_backward?????????0.22%??????20.025ms????????36.33%????????3.348s???????1.674ms??????????2000??
????????????????????????MkldnnConvolutionBackward?????????0.21%??????19.112ms????????36.53%????????3.367s???????1.684ms??????????2000??
??????????????????????????????????????aten::relu_?????????0.20%??????18.611ms?????????0.76%??????70.289ms??????41.346us??????????1700??
?????????????????????aten::_batch_norm_impl_index?????????0.16%??????14.298ms????????15.32%????????1.413s?????706.254us??????????2000??
??????????????????????????????????????aten::addmm?????????0.14%??????12.684ms?????????0.15%??????14.138ms?????141.377us???????????100??
??????????????????????????????????????aten::fill_?????????0.14%??????12.672ms?????????0.14%??????12.672ms??????21.120us???????????600??
????????????????????????????????????ReluBackward1?????????0.13%??????11.845ms?????????1.29%?????119.228ms??????70.134us??????????1700??
????????????????????????????????aten::as_strided_?????????0.13%??????11.674ms?????????0.13%??????11.674ms???????1.946us??????????6000??
????????????????????????????????????????aten::div?????????0.11%??????10.246ms?????????0.13%??????12.288ms?????122.876us???????????100??
?????????????????????????????????aten::batch_norm?????????0.10%???????8.894ms????????15.42%????????1.421s?????710.700us??????????2000??
????????????????????????????????aten::convolution?????????0.08%???????7.478ms????????17.71%????????1.632s?????815.997us??????????2000??
????????????????????????????????????????aten::sum?????????0.08%???????7.066ms?????????0.10%???????9.424ms??????31.415us???????????300??
?????????????????????????????????????aten::conv2d?????????0.07%???????6.851ms????????17.78%????????1.639s?????819.423us??????????2000??
?????????????????????????????????aten::contiguous?????????0.06%???????5.597ms?????????0.06%???????5.597ms???????0.903us??????????6200??
??????????????????????????????????????aten::copy_?????????0.04%???????3.759ms?????????0.04%???????3.980ms???????7.959us???????????500??
??????????????????????????????????????????aten::t?????????0.04%???????3.526ms?????????0.06%???????5.561ms??????11.122us???????????500??
???????????????????????????????????????aten::view?????????0.03%???????2.611ms?????????0.03%???????2.611ms???????8.702us???????????300??
???????????????????????????????????????aten::div_?????????0.02%???????1.973ms?????????0.04%???????4.051ms??????40.512us???????????100??
?????????????????????????????????????aten::expand?????????0.02%???????1.720ms?????????0.02%???????2.225ms???????7.415us???????????300??
????????????????????????????????????AddmmBackward?????????0.02%???????1.601ms?????????0.37%??????34.141ms?????341.414us???????????100??
?????????????????????????????????????????aten::to?????????0.02%???????1.596ms?????????0.04%???????3.871ms??????12.902us???????????300??
???????????????????????????????????????aten::mean?????????0.02%???????1.485ms?????????0.10%???????9.204ms??????92.035us???????????100??
?????????????????????????????????????AddBackward0?????????0.01%???????1.381ms?????????0.01%???????1.381ms???????1.726us???????????800??
??????????????????????????????????aten::transpose?????????0.01%???????1.297ms?????????0.02%???????2.035ms???????4.071us???????????500??
??????????????????????????????aten::empty_strided?????????0.01%???????1.163ms?????????0.01%???????1.163ms???????3.877us???????????300??
?????????????????????MaxPool2DWithIndicesBackward?????????0.01%???????1.095ms?????????1.03%??????94.802ms?????948.018us???????????100??
????????????????????????????????????MeanBackward1?????????0.01%?????974.822us?????????0.16%??????14.393ms?????143.931us???????????100??
????????????????????????????????????aten::resize_?????????0.01%?????911.689us?????????0.01%?????911.689us???????3.039us???????????300??
?????????????????????????????????aten::zeros_like?????????0.01%?????884.496us?????????0.11%??????10.384ms?????103.843us???????????100??
??????????????????????????????????????aten::clone?????????0.01%?????798.993us?????????0.04%???????3.687ms??????18.435us???????????200??
????????????????????????????????????aten::reshape?????????0.01%?????763.804us?????????0.03%???????2.604ms??????13.021us???????????200??
??????????????????????????????????????aten::zero_?????????0.01%?????689.598us?????????0.13%??????11.919ms??????59.595us???????????200??
?????????????????????????????????aten::resize_as_?????????0.01%?????562.349us?????????0.01%?????776.967us???????7.770us???????????100??
?????????????????????????????????aten::max_pool2d?????????0.01%?????492.109us?????????9.49%?????874.295ms???????8.743ms???????????100??
????????????????????????aten::adaptive_avg_pool2d?????????0.01%?????469.736us?????????0.10%???????9.673ms??????96.733us???????????100??
??????????????????????????????????aten::ones_like?????????0.00%?????460.352us?????????0.01%???????1.377ms??????13.766us???????????100??
?????????????????????????????????????SumBackward0?????????0.00%?????399.188us?????????0.01%???????1.206ms??????12.057us???????????100??
????????????????????????????????????aten::flatten?????????0.00%?????397.053us?????????0.02%???????1.917ms??????19.165us???????????100??
?????????????????????????????????????ViewBackward?????????0.00%?????351.824us?????????0.02%???????1.436ms??????14.365us???????????100??
????????????????????????????????????????TBackward?????????0.00%?????308.947us?????????0.01%???????1.315ms??????13.150us???????????100??
???????????????????????????????????????????detach?????????0.00%?????127.329us?????????0.00%?????127.329us???????2.021us????????????63??
???????????????????????torch::autograd::GraphRoot?????????0.00%?????114.731us?????????0.00%?????114.731us???????1.147us???????????100??
?????????????????????????????????????aten::detach?????????0.00%?????106.170us?????????0.00%?????233.499us???????3.706us????????????63??
????---------------------------------------------??------------??------------??------------??------------??------------??------------??
????Self?CPU?time?total:?9.217s

Reference

[1] Automatic differentiation package - torch.autograd — PyTorch 1.7.0 documentation

[2]Autograd