如何判斷一個(gè)點(diǎn)是否落在一個(gè)平面內(nèi)
最近有個(gè)朋友問起的一個(gè)問題,給定一個(gè)荷質(zhì)比和保留時(shí)間構(gòu)成的平面,想看下哪些化合物落在這個(gè)平面里面。
假如有下面一個(gè)平面,哪些點(diǎn)在平面里?哪些點(diǎn)在平面外?怎么判斷呢?
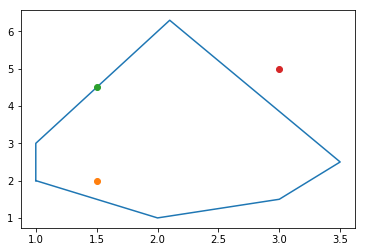
最簡單的方法是目測!
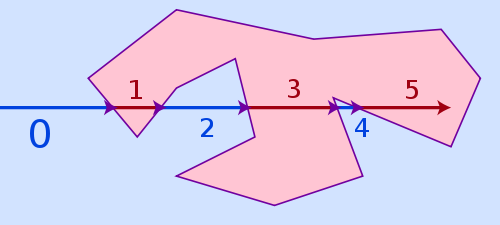
如果采用程序,其中一個(gè)方法是光線投射算法,如下圖所示:從任意位置畫一條到目標(biāo)點(diǎn)的水平線,計(jì)算該水平線進(jìn)出平面邊界的次數(shù),如果是偶數(shù),則點(diǎn)在平面外;如果是奇數(shù),則點(diǎn)在平面內(nèi)。點(diǎn)正好落在定點(diǎn)或邊界時(shí)會出現(xiàn)特殊的判斷。
我們自己構(gòu)造一個(gè)多邊形,繪制幾個(gè)點(diǎn):
# (1.5,2)bounding_points = [(1,2),(2,1),(3,1.5),(3.5,2.5),(2.1,6.3),(1,3)]
bounding_box_positions = [(1.5,2), (1.5,4.5), (3,5)]如下圖
plotPolygenAndPoints(bounding_points, bounding_box_positions)
加上從左側(cè)發(fā)過來的光線
plotPolygenAndPoints(bounding_points, bounding_box_positions, ray=True)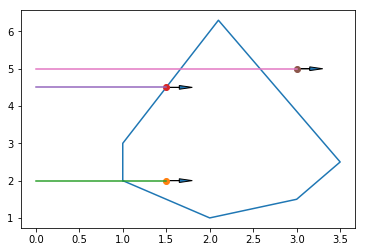
原始函數(shù)不能區(qū)分部分邊界上的點(diǎn)
Stack Overflow上提供了一個(gè)函數(shù)polygon_ray_casting (代碼見文末)實(shí)現(xiàn)ray casting算法,被轉(zhuǎn)換成了各個(gè)程序語言的版本。
測試下這個(gè)函數(shù),一個(gè)邊界點(diǎn)(1.5,4.5)計(jì)算為在平面內(nèi),另一個(gè)邊界點(diǎn)(2.5,1.25)卻未落在邊界內(nèi)。
bounding_box_positions = [(1.5,2), (1,1.25),(1.5,4.5), (3,3),(4,3.1),(2.5,1.25),(3,5),(1.0,2),(3.5,2.5)]
bounding_box_positions = sorted(bounding_box_positions, key=lambda x:x[0])
polygon_ray_casting(bounding_points, bounding_box_positions)[(3, 3), (3.5, 2.5)]關(guān)于這個(gè)結(jié)果在評論區(qū)也有討論,函數(shù)設(shè)計(jì)的目的不同,行為也會不同。在公共平臺找到的代碼和方法是給我們提供思路的,有些代碼可以直接用,有些代碼需要修改后用。使用前,要注意其使用條件,測試后再用于自己的數(shù)據(jù)。
修改后的函數(shù)可處理邊界點(diǎn)
增加邊界點(diǎn)的判斷、定點(diǎn)的判斷增加邊界點(diǎn)的判斷、定點(diǎn)的判斷
測試凸多邊形
# 默認(rèn)落在邊界也算polygon_ray_casting_modi(bounding_points, bounding_box_positions)[(1.0, 2), (3, 3), (3.5, 2.5)]plotPolygenAndPoints(bounding_points, bounding_box_positions)
# 落在邊上不算在內(nèi)polygon_ray_casting_modi(bounding_points, bounding_box_positions, edgeAsInside=False)[(1.5, 2), (3, 3)]測試凹多邊形
# (1.5,2)bounding_points = [(1,2),(2,2.5),(3,1.5),(4,2),(2.1,4),(1,3)]
bounding_box_positions = [(1.5,2), (1,1.25), (1.5,2.5), (3,1.5), (3,3),(4,3.1), (1,2.1), (3.5,1.75)]
bounding_box_positions = sorted(bounding_box_positions, key=lambda x:x[0])
polygon_ray_casting_modi(bounding_points, bounding_box_positions)[(1, 2.1), (1.5, 2.5), (3, 1.5), (3, 3), (3.5, 1.75)]plotPolygenAndPoints(bounding_points, bounding_box_positions)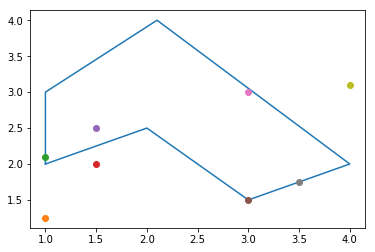
測試多種六邊形
bounding_points = [(1,3),(2,3),(3,2),(2,1),(1,1),(0,2)]
bounding_box_positions = [(-1,3), (1.5,2.9), (1.5,3),(0,2),(1,3),(0.5,1.5),(2.5,1.5), (2.5,3),(0,1.5),(1,1.1)]
bounding_box_positions = sorted(bounding_box_positions, key=lambda x:x[0])
polygon_ray_casting_modi(bounding_points, bounding_box_positions)[(0, 2), (0.5, 1.5), (1, 3), (1, 1.1), (1.5, 2.9), (1.5, 3), (2.5, 1.5)]plotPolygenAndPoints(bounding_points, bounding_box_positions)
# (1.5,2)bounding_points = [(1,3),(2,3),(2,2),(3,2),(3,1),(1,1)]
bounding_box_positions = [(1.5,2), (1.5,3), (1,3), (3,1.25), (3,3)]
polygon_ray_casting_modi(bounding_points, bounding_box_positions)[(1.5, 2), (1.5, 3), (1, 3), (3, 1.25)]plotPolygenAndPoints(bounding_points, bounding_box_positions)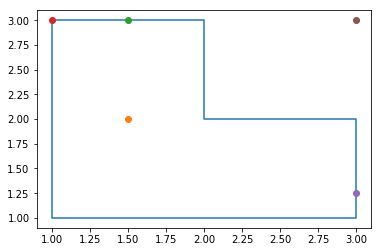
# (1.5,2)bounding_points = [(1,2),(3,2),(3,3),(4,3),(4,1),(1,1)]
bounding_box_positions = [(1.5,2), (1,1.25), (3,3),(4,3.1)]
polygon_ray_casting_modi(bounding_points, bounding_box_positions)[(1.5, 2), (1, 1.25), (3, 3)]plotPolygenAndPoints(bounding_points, bounding_box_positions)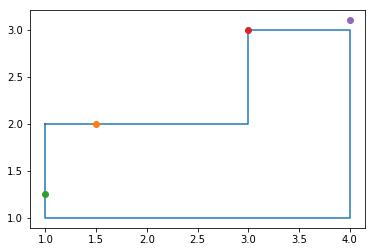
for i in bounding_box_positions:
print(i)
print(wn_PnPoly(i, bounding_points))(1.5, 2)
0
(1, 1.25)
-1
(3, 3)
0
(4, 3.1)
0用到的繪圖函數(shù)
import matplotlib.pyplot as pltdef plotPolygenAndPoints(bounding_points, bounding_box_positions, ray=False):
coord = bounding_points[:]
coord.append(coord[0]) #repeat the first point to create a 'closed loop'
xs, ys = zip(*coord) #create lists of x and y values
plt.figure()
plt.plot(xs,ys)
for x,y in bounding_box_positions:
plt.plot(x,y,'o') if ray:
plt.plot((0,x),(y,y))
plt.arrow(x, y, 0.3, 0, shape='full', lw=1, length_includes_head=True, head_width=.1)
plt.show()用到的判斷函數(shù)
def polygon_ray_casting(bounding_points, bounding_box_positions):
# https://wrf.ecse.rpi.edu/Research/Short_Notes/pnpoly.html
# https://stackoverflow.com/questions/217578/how-can-i-determine-whether-a-2d-point-is-within-a-polygon
# Arrays containing the x- and y-coordinates of the polygon's vertices.
vertx = [point[0] for point in bounding_points]
verty = [point[1] for point in bounding_points] # Number of vertices in the polygon
nvert = len(bounding_points) # Points that are inside
points_inside = [] # For every candidate position within the bounding box
for idx, pos in enumerate(bounding_box_positions):
testx, testy = (pos[0], pos[1])
c = 0
for i in range(0, nvert):
j = i - 1 if i != 0 else nvert - 1
if( ((verty[i] > testy ) != (verty[j] > testy)) and
(testx < (vertx[j] - vertx[i]) * (testy - verty[i]) / (verty[j] - verty[i]) + vertx[i]) ):
c += 1
# If odd, that means that we are inside the polygon
if c % 2 == 1:
points_inside.append(pos) return points_inside最終用的函數(shù)
def between(a,x,y,equal=True, epsilon=0.000001):
if equal: return (x<=a<=y) or (x>=a>=y) or (abs(a-x)<epsilon) or (abs(a-y)<epsilon) else: return (x<a<y) or (x>a>y)def polygon_ray_casting_modi(bounding_points, bounding_box_positions, edgeAsInside=True, epsilon=0.000001):
# https://wrf.ecse.rpi.edu/Research/Short_Notes/pnpoly.html
# https://stackoverflow.com/questions/217578/how-can-i-determine-whether-a-2d-point-is-within-a-polygon
# Arrays containing the x- and y-coordinates of the polygon's vertices.
vertx = [point[0] for point in bounding_points]
verty = [point[1] for point in bounding_points] # Number of vertices in the polygon
nvert = len(bounding_points) # Points that are inside
points_inside = [] # For every candidate position within the bounding box
for idx, pos in enumerate(bounding_box_positions):
testx, testy = (pos[0], pos[1])
inside = False
for i in range(0, nvert):
j = i - 1 if i != 0 else nvert - 1
# Point on horizontaol edge
if (verty[i] == testy ) and (verty[j] == testy) and between(testx, vertx[i],vertx[j]):
inside = edgeAsInside break
# corner point
if (((verty[i] == testy) and (vertx[i] == testx)) or ((verty[j] == testy) and (vertx[j]==testx))):
inside = edgeAsInside break
if between(testy, verty[i], verty[j]): if(testy==verty[i]<=verty[j]) or (testy==verty[j]<=verty[i]): continue
c = (vertx[i]-testx)*(verty[j]-testy) - (vertx[j]-testx)*(verty[i]-testy) # print(c)
if c==0 or abs(c) < epsilon:
inside = edgeAsInside break
if (verty[i]<verty[j]) == (c>0):
inside = not inside # If odd, that means that we are inside the polygon
#print(inside)
if inside:
points_inside.append(pos) return points_inside參考
https://stackoverflow.com/questions/8721406/how-to-determine-if-a-point-is-inside-a-2d-convex-polygon/23223947#23223947
https://github.com/mikolalysenko/robust-point-in-polygon
https://wrf.ecse.rpi.edu//Research/Short_Notes/pnpoly.html
https://stackoverflow.com/questions/217578/how-can-i-determine-whether-a-2d-point-is-within-a-polygon?page=1&tab=votes#tab-top
https://en.m.wikipedia.org/wiki/Point_in_polygon
完整代碼 https://gitee.com/ct5869/shengxin-baodian
往期精品(點(diǎn)擊圖片直達(dá)文字對應(yīng)教程)
后臺回復(fù)“生信寶典福利第一波”或點(diǎn)擊閱讀原文獲取教程合集




























