大家好

我早期入門數(shù)據(jù)分析的時候曾對數(shù)據(jù)可視化比較癡迷，積累了很多文檔、代碼、圖例，最近花了點時間重新整理了一遍。發(fā)現(xiàn)之前還真是寫了很多東西，現(xiàn)在看來都是極簡單和入門，有點不值一提。

但不知道有沒有剛?cè)腴T的同學恰好需要，先看下主要內(nèi)容吧：

• 基礎的散點圖、折線圖、柱狀圖、直方圖、餅圖、箱線圖
• 配合實例的探索性數(shù)據(jù)分析常用圖表
• 漏斗圖、詞云圖、動態(tài)排序圖、R風格圖、交互式圖、南丁格爾玫瑰圖、缺失值矩陣圖、漫畫風格圖、桑吉圖、和弦圖、餅樹圖
• 也有一些圖沒有寫文檔，只保留了代碼，比如氣泡圖、山巒疊嶂圖、甘特圖、極坐標圖
• 中間也涉及Matplotlib、Seaborn、Bokeh、plotly、Chartify等繪圖庫的入門

配套的數(shù)據(jù)集、代碼、文檔和示例圖很完整（付費讀者文末可下載），2萬余字，100余張示例圖。

定價29元，感興趣的同學支持一波吧。

想白嫖的同學，可以在本公眾號挨個搜索關(guān)鍵詞，其實大部分都有寫過免費文章，只是沒有本文整理的完善，代碼可能也不完整，不影響學習。

正文：

探索性數(shù)據(jù)分析常用圖表

探索性數(shù)據(jù)分析（EDA）階段為機器學習項目中至關(guān)重要的環(huán)節(jié)，我們以廣告渠道對銷量的影響數(shù)據(jù)集為例，即電視廣告(TV)，報紙廣告(Newspaper)，和廣播廣告(Radio)對于產(chǎn)品銷量的影響。一個公司同時通過這三種廣告媒介進行宣傳，在不同的廣告預算下，產(chǎn)品銷量也不同。我們希望通過數(shù)據(jù)分析了解不同的廣告渠道對銷量有什么影響，并最大化廣告對于銷量的增益。本節(jié)，我們用可視化的方式，對數(shù)據(jù)集做個探索性數(shù)據(jù)分析。

導入庫&數(shù)據(jù)

# -*- coding: utf-8 -*-
# 導入庫

import pandas as pd

import seaborn as sns

import matplotlib.pyplot as plt

# 導入數(shù)據(jù)

df=pd.read_csv('..\Advertising.csv')

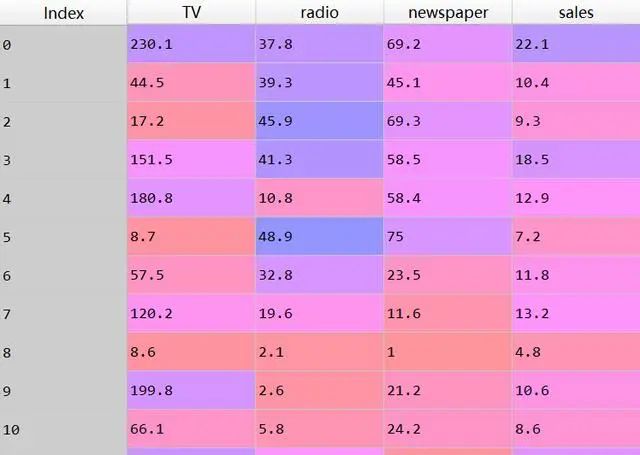
數(shù)據(jù)分布

先看一下數(shù)據(jù)分布情況

df.hist(xlabelsize=10,ylabelsize=10,figsize=(16,12))

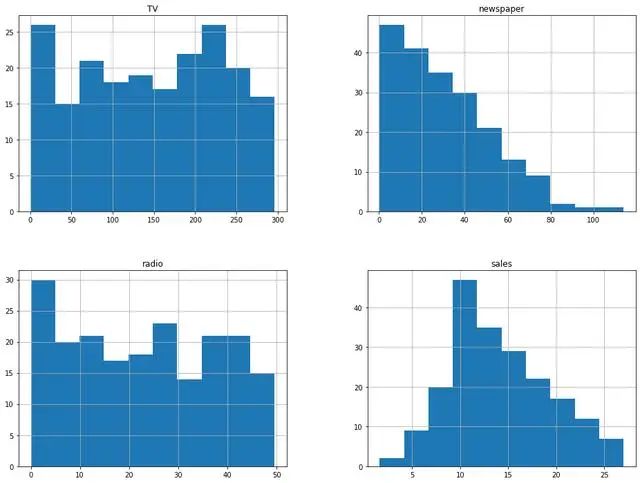
箱形圖

箱形圖（Box-plot）又稱為盒須圖、盒式圖或箱線圖，是一種用作顯示一組數(shù)據(jù)分散情況資料的統(tǒng)計圖。它主要用于反映原始數(shù)據(jù)分布的特征，還可以進行多組數(shù)據(jù)分布特征的比 較。箱線圖的繪制方法是：先找出一組數(shù)據(jù)的上邊緣、下邊緣、中位數(shù)和兩個四分位數(shù)；然后， 連接兩個四分位數(shù)畫出箱體；再將上邊緣和下邊緣與箱體相連接，中位數(shù)在箱體中間。

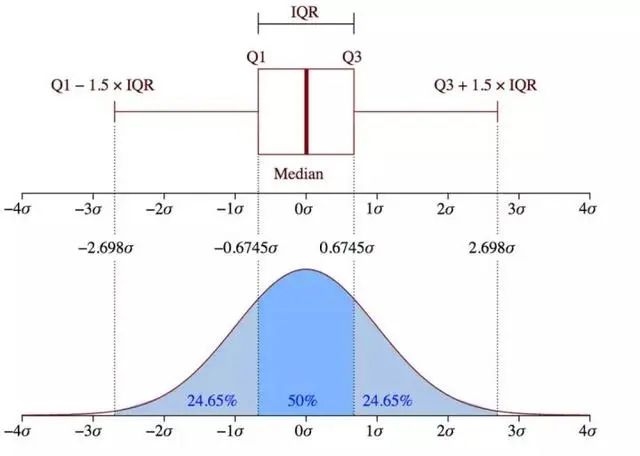
四分位距(IQR)就是上四分位與下四分位的差值。而我們通過IQR的1.5倍為標準，規(guī)定：超過（上四分位+1.5倍IQR距離，或者下四分位-1.5倍IQR距離）的點為異常值。

plt.subplots(figsize=(15,10)) sns.boxplot(data=df)

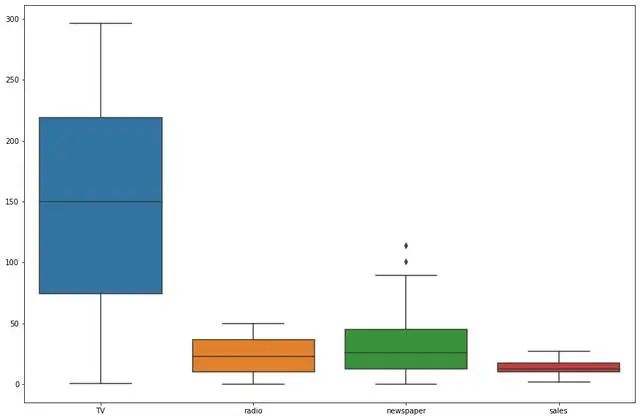
可以看出newspaper是存在異常值，異常值處理可以用missinggo處理，之后會講，這里就不講了。

矩陣圖

矩陣圖法就是從多維問題的事件中，找出成對的因素，排列成矩陣圖，然后根據(jù)矩陣圖來分析問題，確定關(guān)鍵點的方法。它是一種通過多因素綜合思考，探索問題的好方法。從問題事項中找出成對的因素群，分別排列成行和列，找出其中行與列的相關(guān)性或相關(guān)程度大小的一種方法。

sns.pairplot(df, kind="reg")

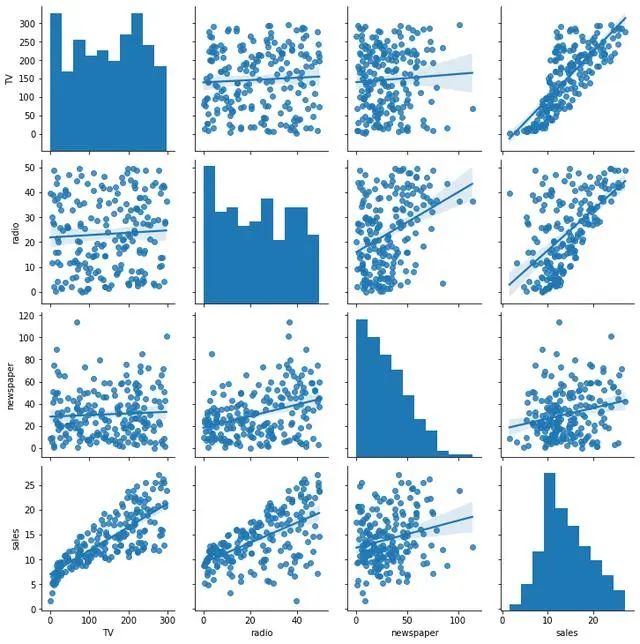
相關(guān)圖

相關(guān)圖是研究相關(guān)關(guān)系的直觀工具。一般在進行詳細的定量分析之前，可利用相關(guān)圖對現(xiàn)象之間存在的相關(guān)關(guān)系的方向、形式和密切程度進行大致的判斷。變量之間的相關(guān)關(guān)系可以簡單分為四種表現(xiàn)形式，分別有：正線性相關(guān)、負線性相關(guān)、非線性相關(guān)和不相關(guān)，從圖形上各點的分散程度即可判斷兩變量間關(guān)系的密切程度。

plt.subplots(figsize=(15,10))
sns.heatmap(df.corr(), xticklabels=df.corr().columns, yticklabels=df.corr().columns, cmap='RdYlGn', center=0, annot=True)

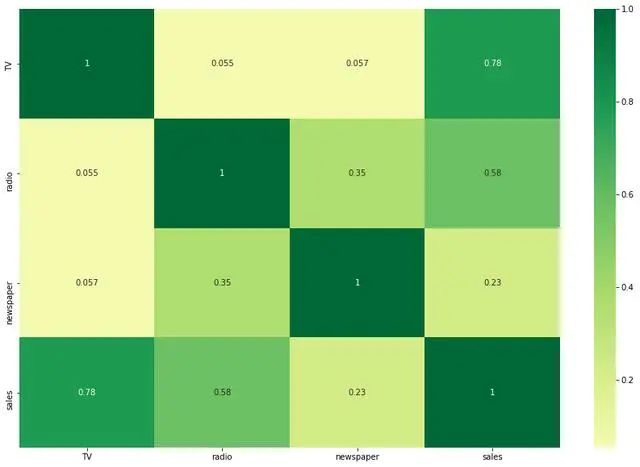
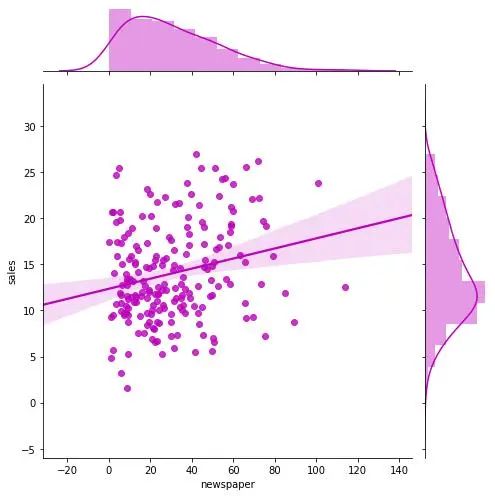
帶線性回歸最佳擬合線的散點圖

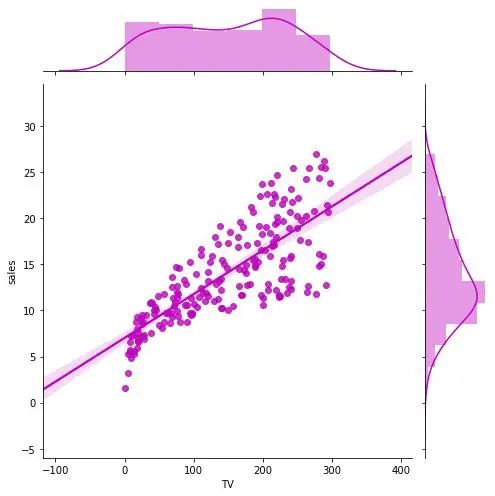
如果你想了解兩個變量如何相互改變，那么最佳擬合線就是常用的方法。我在圖中還加入了 沿 X 和 Y 軸變量的邊緣直方圖，用于可視化 X 和 Y 之間的關(guān)系以及單獨的 X 和 Y 的單變量分布。

g_TV = sns.jointplot("TV", "sales", data=df,

kind="reg", truncate=False,

color="m", height=7)

g_radio = sns.jointplot("radio", "sales", data=df,

kind="reg", truncate=False,

color="m", height=7)

g_newspaper = sns.jointplot("newspaper", "sales", data=df,

kind="reg", truncate=False,

color="m", height=7)

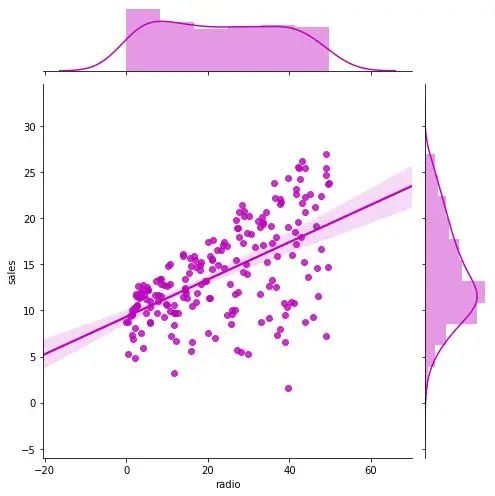
重溫探索性數(shù)據(jù)分析

探索性數(shù)據(jù)分析是進行建模分析之前的相當關(guān)鍵的步驟，它是幫助大家熟悉數(shù)據(jù)并且探索數(shù)據(jù)的過程。在EDA的過程中，你能探索到越多的數(shù)據(jù)特性，在建模的過程中就越高效。

我們以UCI機器學習庫中「銀行營銷數(shù)據(jù)集」為例，根據(jù)相關(guān)的信息預測通過電話推銷，用戶是否會在銀行進行存款。我們用可視化的方式，認識一下幾個重要特征。

數(shù)值型的特征可以用箱型圖查看其分布情況，這樣也可以查找異常值。

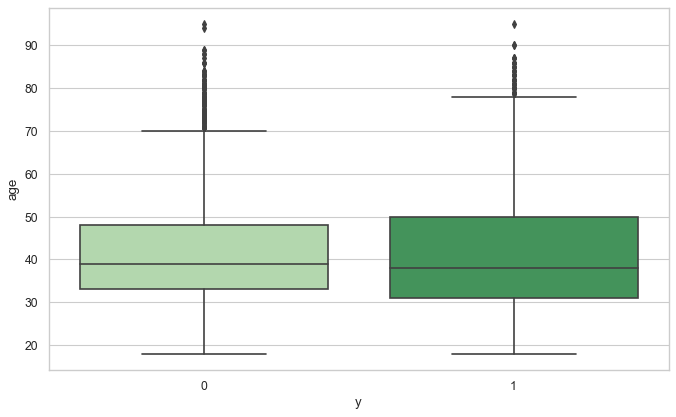概率密度圖也是不錯的選擇

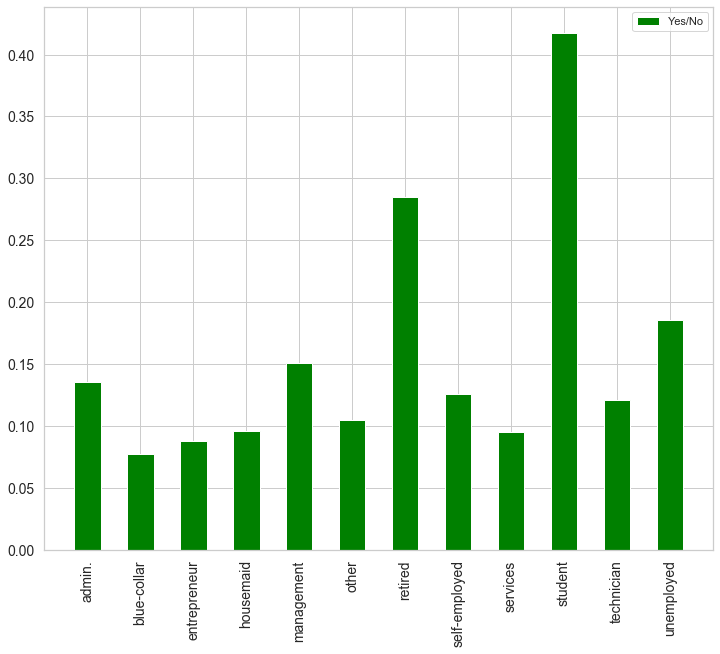
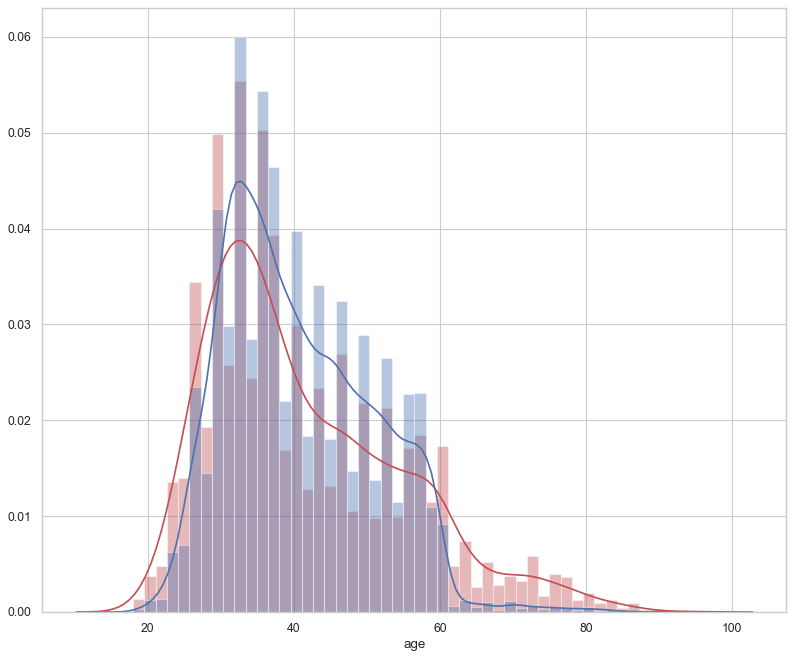分類型數(shù)據(jù)的分布情況探查主要是查看各個分類值出現(xiàn)的頻次及趨勢，可以用柱狀圖直觀展示。

如果要同時觀察多個變量之間的相互關(guān)系，比較常用的就是seaborn中的pairplot方法。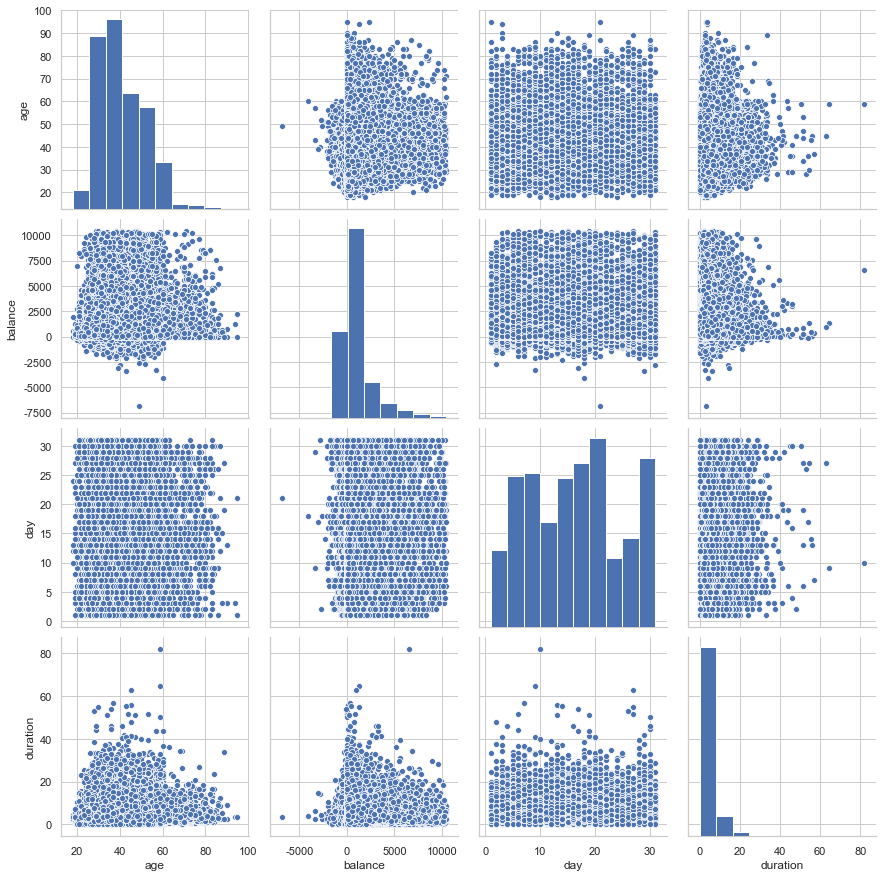

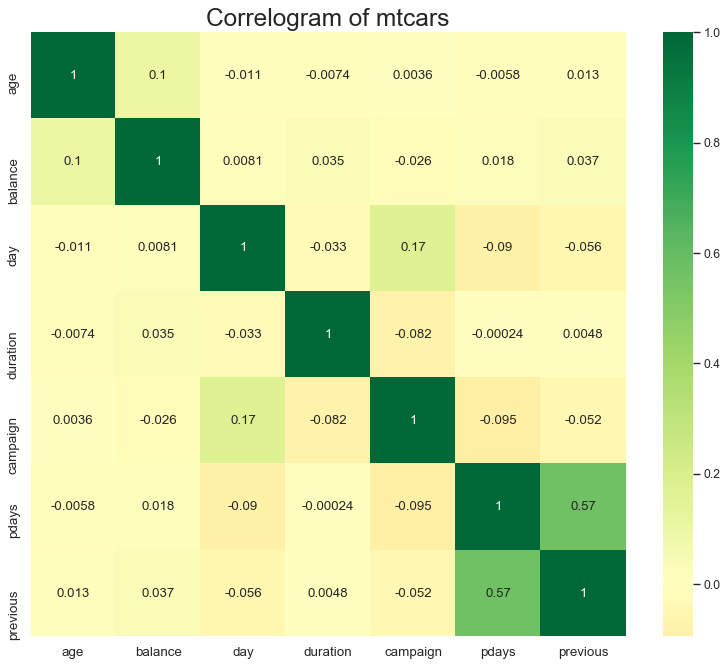
想要具體查看多個聯(lián)系性特征之間的相關(guān)系數(shù)，heatmap是個不錯的選擇。

特征深入研究

這一部分我使用了員工離職數(shù)據(jù)集，數(shù)據(jù)主要包括影響員工離職的各種因素（工資、績效、工作滿意度、參加項目數(shù)、工作時長、是否升職等）以及員工是否已經(jīng)離職的對應記錄。我們需要分析這14999個樣本以及10個特征, 通過現(xiàn)有員工已經(jīng)是否離職的數(shù)據(jù), 尋找員工離職原因。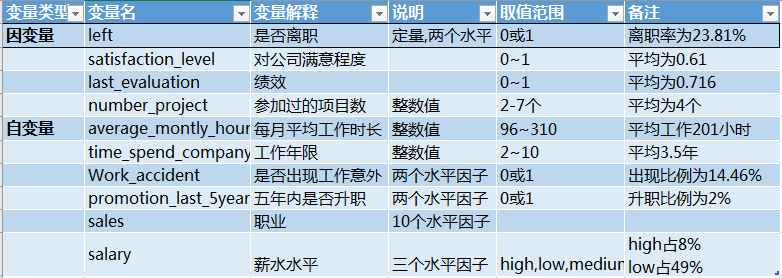

大家可以猜一下，以下幾個特征的可視化是用什么方法實現(xiàn)的？

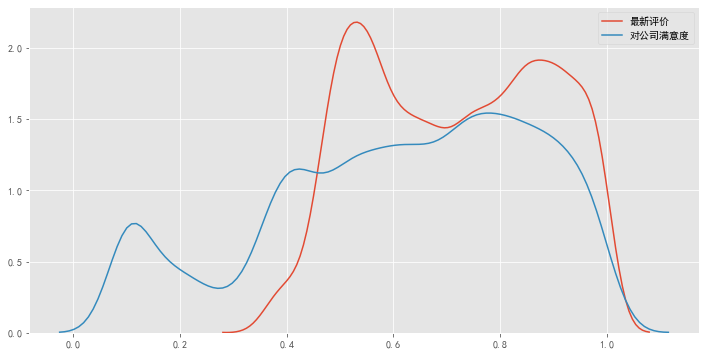
數(shù)據(jù)特征分析：對公司的滿意度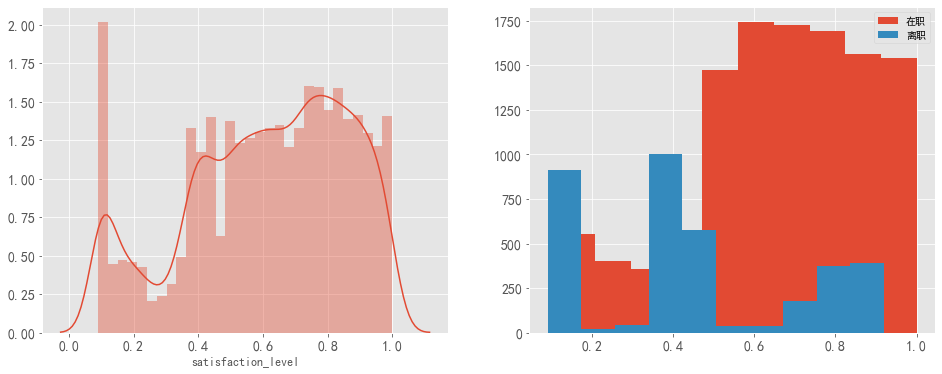

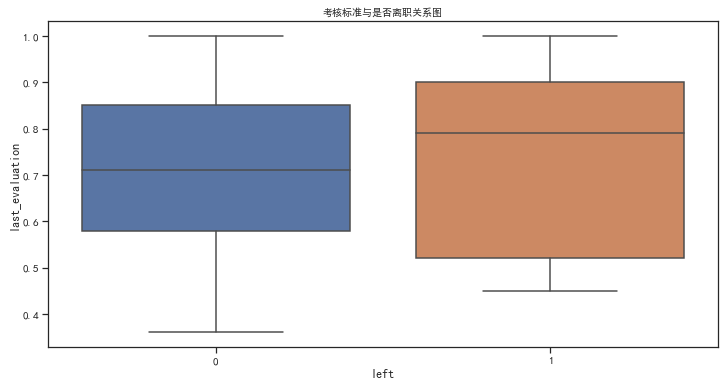
數(shù)據(jù)特征分析：最新考核評估

數(shù)據(jù)特征分析：工作年限、每月平均工作時長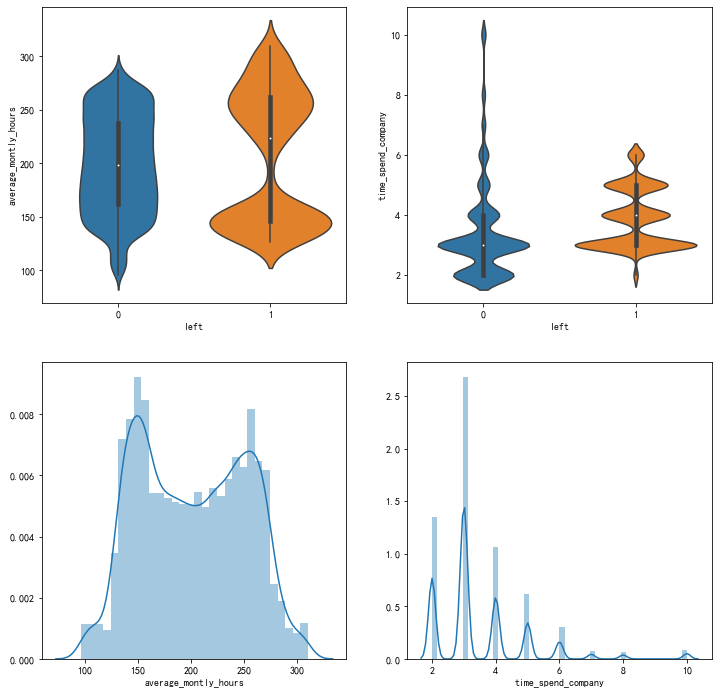

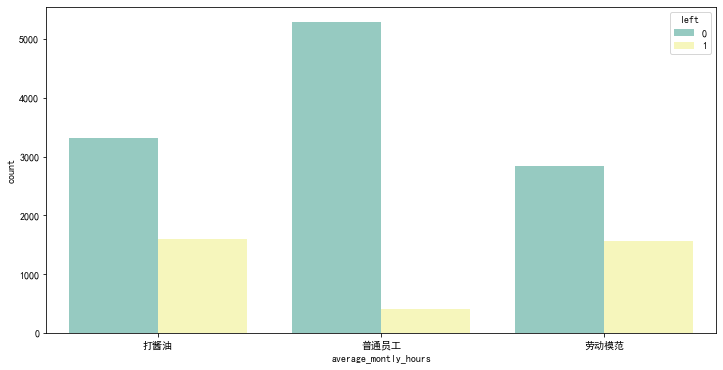
數(shù)據(jù)特征分析：工作事故、五年內(nèi)是否升職、工資水平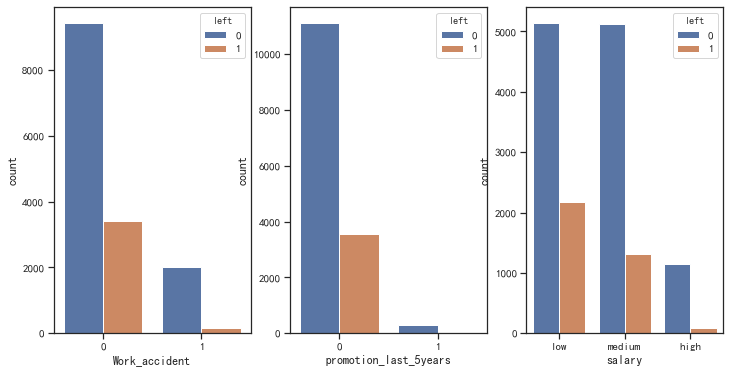

數(shù)據(jù)變換、數(shù)據(jù)標準化、特征離散

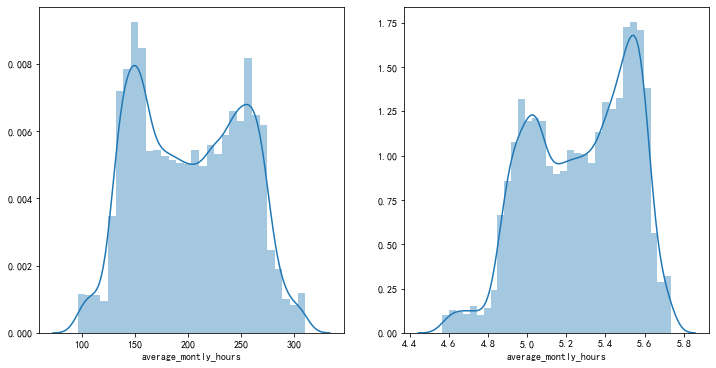
數(shù)據(jù)可視化還可以用于觀察數(shù)據(jù)變換的前后對比，這里我依然使用員工離職數(shù)據(jù)集。

• 數(shù)據(jù)log變換的可視化

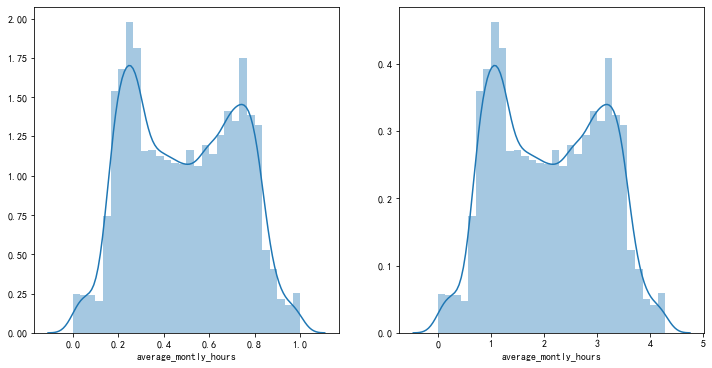
• 數(shù)據(jù)標準化的可視化

• 特征離散化的可視化

matplotlib、seaborn、pyecharts、Altair分別繪制柱狀圖。

導入庫&數(shù)據(jù)

# 引入模塊
import numpy as np
import pandas as pd
import altair as alt

import plotly.express as px
import matplotlib.pyplot as plt

## 導入數(shù)據(jù)
path=r"...\datasets\海外疫情數(shù)據(jù).csv"
df = pd.read_csv(path,encoding='utf-8',header=0)
plt.rcParams['font.sans-serif']=['SimHei']  #用來正常顯示中文標簽
plt.rcParams['axes.unicode_minus'] = False  #用來正常顯負數(shù)

我們使用的是海外國家新冠肺炎疫情數(shù)據(jù)，包括了現(xiàn)存確診、累計確診、治愈、死亡數(shù)據(jù)。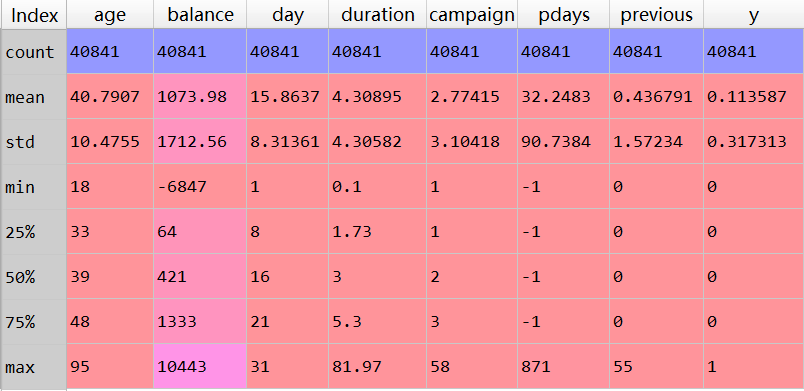

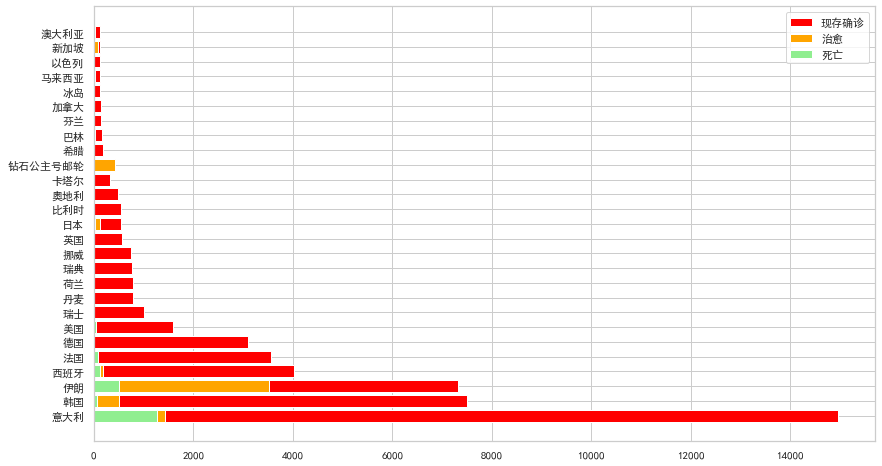
matplotlib

Matplotlib就不用多介紹了，使用最頻繁的Python可視化庫庫。

fig, ax = plt.subplots(figsize=(14,8))
ax.barh( df.國家,df.現(xiàn)存確診,label="現(xiàn)存確診", color='red')
ax.barh( df.國家,df.治愈,label="治愈", color='orange')
ax.barh( df.國家,df.死亡,label="死亡", color='lightgreen')
plt.legend(loc="upper right") 

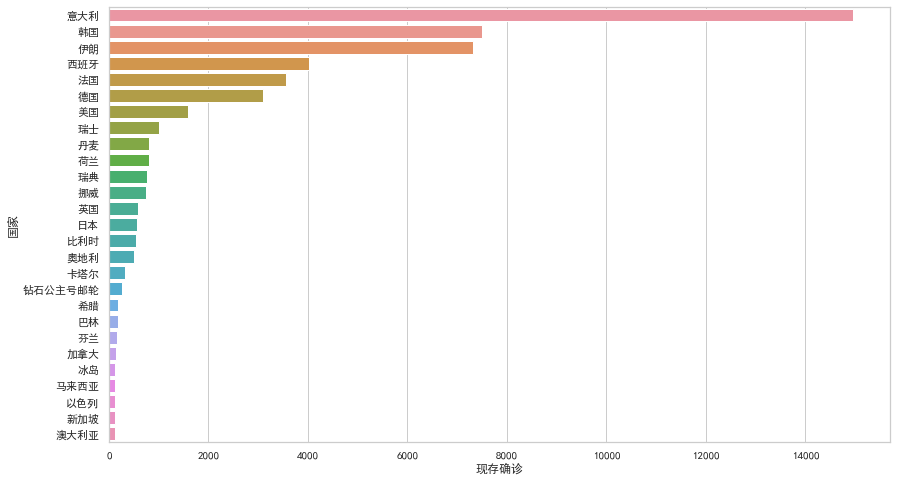
Seaborn

Seaborn利用matplotlib的強大功能，可以只用幾行代碼就創(chuàng)建漂亮的圖表。關(guān)鍵區(qū)別在于Seaborn的默認款式和調(diào)色板設計更加美觀和現(xiàn)代。由于Seaborn是在matplotlib之上構(gòu)建的，因此還需要了解matplotlib以便調(diào)整Seaborn的默認值。

plt.figure(figsize=(14,8))
ax = sns.barplot(x="現(xiàn)存確診", y="國家", data=df)

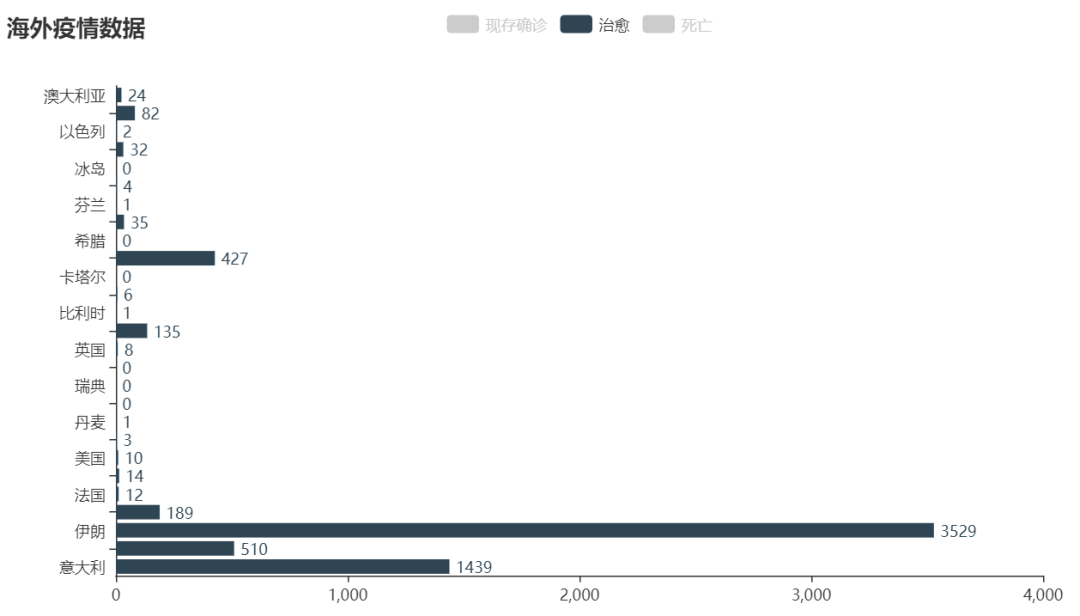
pyecharts

pyecharts 是一個用于生成 Echarts 圖表的類庫。Echarts 是百度開源的一個數(shù)據(jù)可視化 JS 庫。用 Echarts 生成的圖可視化效果非常棒。

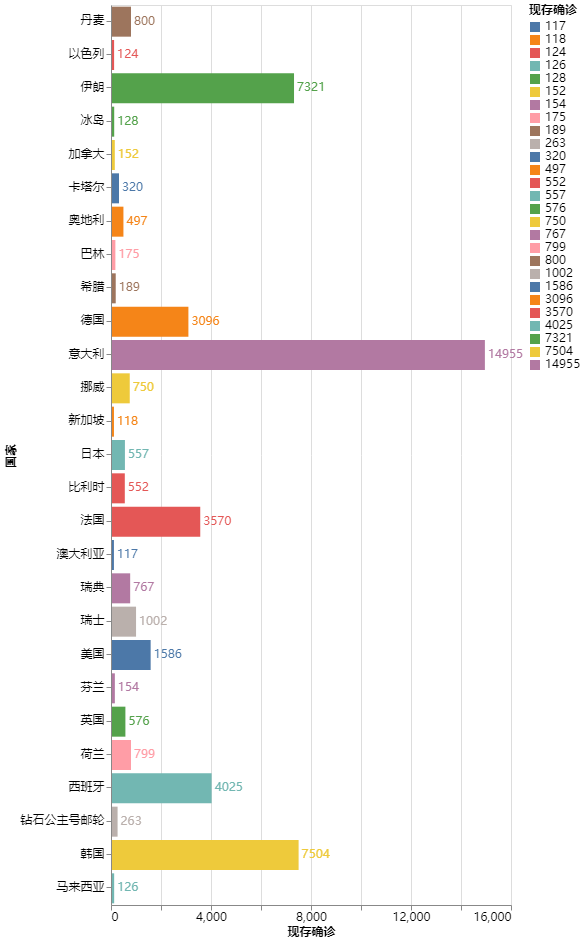
Altair

Altair是一個基于 Vega-lite 的聲明性統(tǒng)計（declarative statistical）可視化python庫。聲明意味著只需要提供數(shù)據(jù)列與編碼通道之間的鏈接，例如x軸，y軸，顏色等，其余的繪圖細節(jié)它會自動處理。聲明使Altair變得簡單，友好和一致。使用Altair可以輕松設計出有效且美觀的可視化代碼。

普通散點圖

散點圖是用于研究兩個變量之間關(guān)系的經(jīng)典的和基本的圖表。 如果數(shù)據(jù)中有多個組，則可能需要以不同顏色可視化每個組。

今天我們畫普通散點圖、邊際分布線性回歸散點圖、散點圖矩陣、帶線性回歸最佳擬合線的散點圖。

在 matplotlib 中，可以使用 plt.scatterplot（） 方便地執(zhí)行此操作。

import matplotlib.pyplot as plt

import numpy as np

N = 10

x = np.random.rand(N)

y = np.random.rand(N)

plt.scatter(x, y)

plt.show()

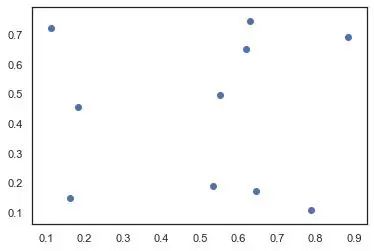
matplotlib散點圖升級版

散點的大小、形狀、顏色和透明度都是可以修改的，來看一個升級版。

import numpy as np

import matplotlib.pyplot as plt

# Fixing random state for reproducibility

np.random.seed(19680801)

N = 50

x = np.random.rand(N)

y = np.random.rand(N)

colors = np.random.rand(N)

area = (30 * np.random.rand(N))**2 # 0 to 15 point radii

plt.scatter(x, y, s=area, c=colors, alpha=0.5)

plt.show()

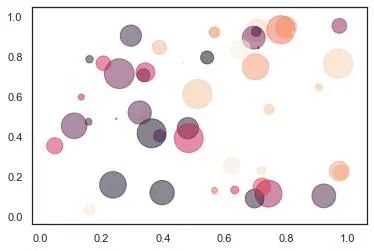
Seaborn散點圖 + 分布圖

#創(chuàng)建數(shù)據(jù)
rs = np.random.RandomState(2)

df = pd.DataFrame(rs.randn(200,2), columns = ['A','B'])

sns.jointplot(x=df['A'], y=df['B'], #設置xy軸，顯示columns名稱

data = df, #設置數(shù)據(jù)

color = 'b', #設置顏色

s = 50, edgecolor = 'w', linewidth = 1,#設置散點大小、邊緣顏色及寬度(只針對scatter)

stat_func=sci.pearsonr,

kind = 'scatter',#設置類型：'scatter','reg','resid','kde','hex'

#stat_func=<function pearsonr>,

space = 0.1, #設置散點圖和布局圖的間距

size = 8, #圖表大小(自動調(diào)整為正方形))

ratio = 5, #散點圖與布局圖高度比，整型

marginal_kws = dict(bins=15, rug =True), #設置柱狀圖箱數(shù)，是否設置rug

)

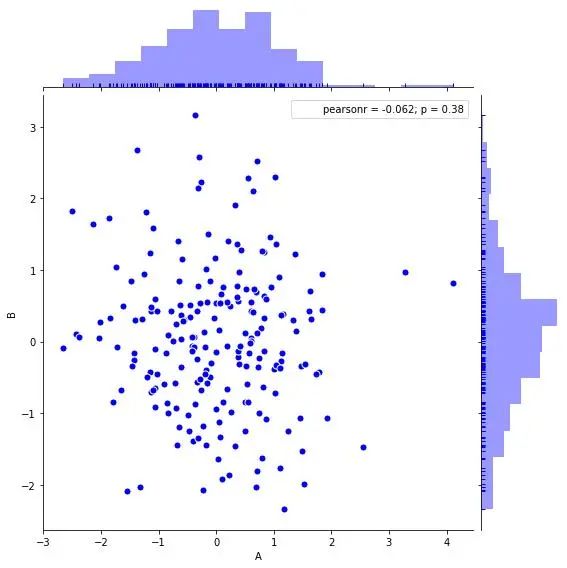
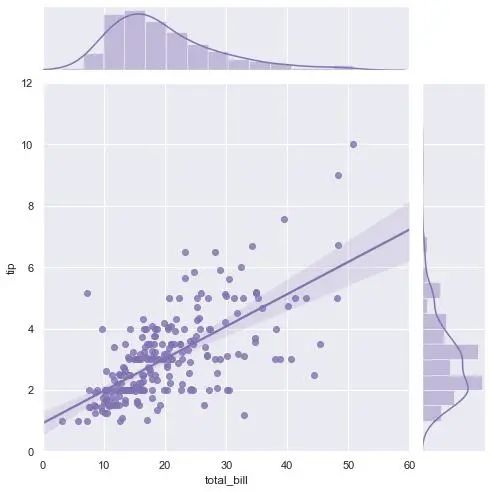
帶線性回歸最佳擬合線的散點圖

如果你想了解兩個變量如何相互改變，那么最佳擬合線就是常用的方法。 下圖顯示了數(shù)據(jù)中各組之間最佳擬合線的差異。 要禁用分組并僅為整個數(shù)據(jù)集繪制一條最佳擬合線，

import seaborn as sns

sns.set(style="darkgrid")

tips = sns.load_dataset("tips")

g = sns.jointplot("total_bill", "tip", data=tips,

kind="reg", truncate=False,

xlim=(0, 60), ylim=(0, 12),

color="m", height=7)

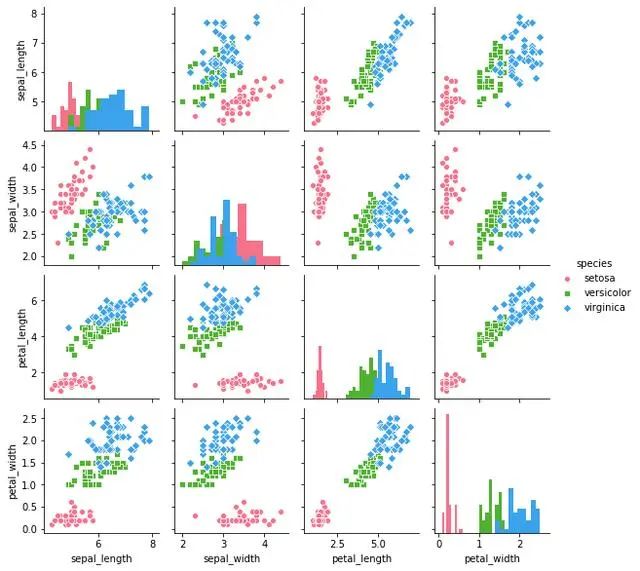
矩陣散點圖 - pairplot()

#設置風格

sns.set_style('white')

#讀取數(shù)據(jù)

iris = sns.load_dataset('iris')

print(iris.head())

sns.pairplot(iris,

kind = 'scatter', #散點圖/回歸分布圖{'scatter', 'reg'})

diag_kind = 'hist', #直方圖/密度圖{'hist'， 'kde'}

hue = 'species', #按照某一字段進行分類

palette = 'husl', #設置調(diào)色板

markers = ['o', 's', 'D'], #設置不同系列的點樣式（這里根據(jù)參考分類個數(shù)）

size = 2 #圖標大小)