教你一步步從統(tǒng)計(jì)學(xué)開(kāi)始入手?jǐn)?shù)據(jù)分析！

統(tǒng)計(jì)學(xué)是在數(shù)據(jù)分析的基礎(chǔ)上，研究如何測(cè)定、收集、整理、歸納和分析反映數(shù)據(jù)數(shù)據(jù)，以便給出正確消息的科學(xué)。如果要學(xué)習(xí)數(shù)據(jù)分析，那么扎實(shí)的統(tǒng)計(jì)知識(shí)是必備的。

本文參考《深入淺出統(tǒng)計(jì)學(xué)》二 、三、 四、 五 章知識(shí)，對(duì)重點(diǎn)內(nèi)容進(jìn)行歸納總結(jié)。最后有幾個(gè)統(tǒng)計(jì)概率應(yīng)用的例子以及使用python分析6家上市公司股票的干貨。

1.均值

平均數(shù)的一般量度:

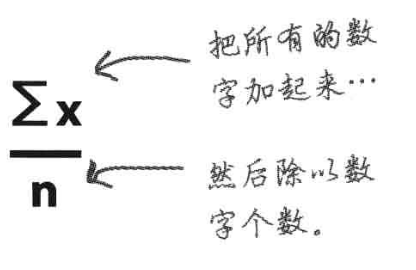
均值公式

有時(shí)候一些數(shù)據(jù)重復(fù)了，這時(shí)候需要用到頻數(shù)：

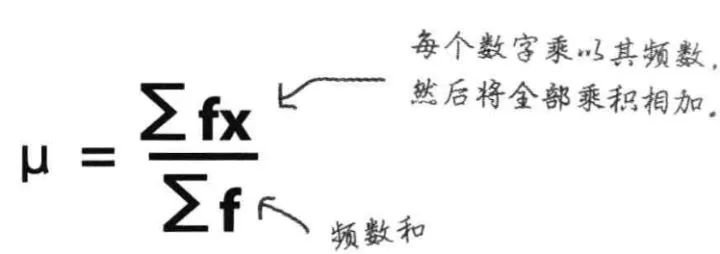頻數(shù)公式

2.中位數(shù)

偏斜數(shù)據(jù)和異常值使均值誤導(dǎo)的時(shí)候，用它，它是中間值。

3.眾數(shù)

數(shù)據(jù)中出現(xiàn)最多的數(shù)值。

4.四分?jǐn)?shù)

四分位數(shù)（Quartile）是統(tǒng)計(jì)學(xué)中分位數(shù)的一種，即把所有數(shù)值由小到大排列并分成四等份，處于三個(gè)分割點(diǎn)位置的數(shù)值就是四分位數(shù)。

注意：由小到大排列。

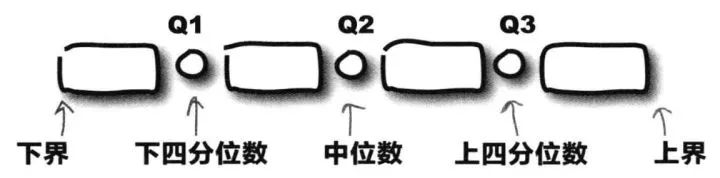
四分位數(shù)

• 第一四分位數(shù) (Q1)：又稱“較小四分位數(shù)”，等于該樣本中所有數(shù)值由小到大排列后第25%的數(shù)字。

• 第二四分位數(shù) (Q2)：又稱“中位數(shù)”，等于該樣本中所有數(shù)值由小到大排列后第50%的數(shù)字。

• 第三四分位數(shù) (Q3)：又稱“較大四分位數(shù)”，等于該樣本中所有數(shù)值由小到大排列后第75%的數(shù)字

第三四分位數(shù)與第一四分位數(shù)的差距又稱四分位距（InterQuartile Range, IQR）。

5.方差

(variance)統(tǒng)計(jì)中的方差（樣本方差）是每個(gè)樣本值與全體樣本值的平均數(shù)之差的平方值的平均數(shù)。

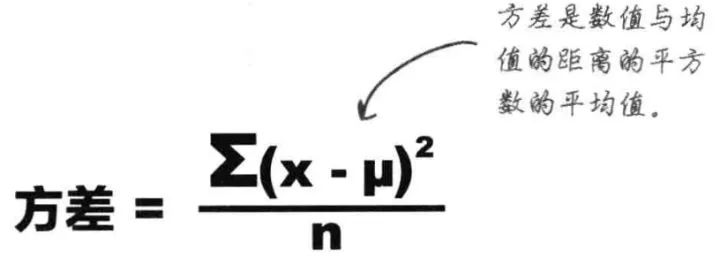
方差

6.標(biāo)準(zhǔn)差(Standard deviation)

離均差平方的算術(shù)平均數(shù)的平方根，用σ表示。標(biāo)準(zhǔn)差是方差的算術(shù)平方根。標(biāo)準(zhǔn)差能反映一個(gè)數(shù)據(jù)集的離散程度。平均數(shù)相同的兩組數(shù)據(jù)，標(biāo)準(zhǔn)差未必相同。

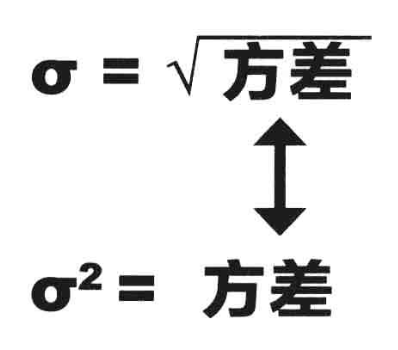
標(biāo)準(zhǔn)差

方差所得的數(shù)值之平方根就是總體的標(biāo)準(zhǔn)偏差。

7.標(biāo)準(zhǔn)分

是一種由原始分推導(dǎo)出來(lái)的相對(duì)地位量數(shù)，它是用來(lái)說(shuō)明原始分在所屬的那批分?jǐn)?shù)中的相對(duì)位置的。

標(biāo)準(zhǔn)分

概率是對(duì)隨機(jī)事件發(fā)生的可能性的度量，一般以一個(gè)在0到1之間的實(shí)數(shù)表示一個(gè)事件發(fā)生的可能性大小。

概率

1.對(duì)立事件

若A交B為不可能事件，A并B為必然事件，那么稱A事件與事件B互為對(duì)立事件，其含義是：事件A和事件B必有一個(gè)且僅有一個(gè)發(fā)生。

對(duì)立事件概率之間的關(guān)系：P(A)+P(B)=1。

例如：在擲骰子試驗(yàn)中，A={出現(xiàn)的點(diǎn)數(shù)為偶數(shù)}，b={出現(xiàn)的點(diǎn)數(shù)為奇數(shù)}，A∩B為不可能事件，A∪B為必然事件，所以A與B互為對(duì)立事件。

2.相交事件

有可能同時(shí)發(fā)生的兩件事。

相交事件

3.互斥事件

兩件事中只可能發(fā)生一件。

拋硬幣，正反面是互斥，拋出正面就不可能有反面。

4.獨(dú)立事件

發(fā)生概率不受其他事件影響。

貝葉斯定理（英語(yǔ)：Bayes' theorem）是概率論中的一個(gè)定理，它跟隨機(jī)變量的條件概率以及邊緣概率分布有關(guān)。在有些關(guān)于概率的解釋中，貝葉斯定理（貝葉斯公式）能夠告知我們?nèi)绾卫眯伦C據(jù)修改已有的看法。這個(gè)名稱來(lái)自於托馬斯·貝葉斯。

在介紹貝葉斯定理之前，先簡(jiǎn)單地介紹一下條件概率，描述的是事件 A 在另一個(gè)事件 B 已經(jīng)發(fā)生條件下的概率，記作P（A|B）， A 和 B 可能是相互獨(dú)立的兩個(gè)事件，也可能不是：

1.期望值

在概率論和統(tǒng)計(jì)學(xué)中，一個(gè)離散性隨機(jī)變量的期望值（或數(shù)學(xué)期望、或均值，亦簡(jiǎn)稱期望，物理學(xué)中稱為期待值）是試驗(yàn)中每次可能的結(jié)果乘以其結(jié)果概率的總和。

2.夏普比率

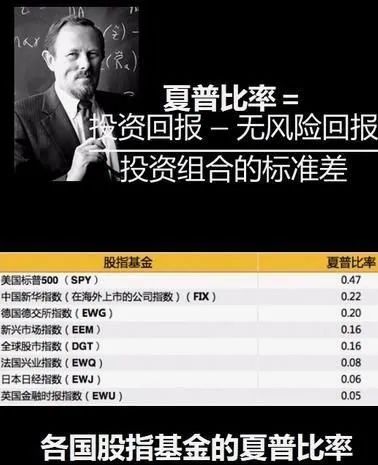
現(xiàn)代投資理論的研究表明,風(fēng)險(xiǎn)的大小在決定組合的表現(xiàn)上具有基礎(chǔ)性的作用。風(fēng)險(xiǎn)調(diào)整后的收益率就是一個(gè)可以同時(shí)對(duì)收益與風(fēng)險(xiǎn)加以考慮的綜合指標(biāo),以期能夠排除風(fēng)險(xiǎn)因素對(duì)績(jī)效評(píng)估的不利影響。夏普比率就是一個(gè)可以同時(shí)對(duì)收益與風(fēng)險(xiǎn)加以綜合考慮的三大經(jīng)典指標(biāo)之一。

如果夏普比率為正值，說(shuō)明在衡量期內(nèi)基金的平均凈值增長(zhǎng)率超過(guò)了無(wú)風(fēng)險(xiǎn)利率，在以同期銀行存款利率作為無(wú)風(fēng)險(xiǎn)利率的情況下，說(shuō)明投資基金比銀行存款要好。夏普比率越大，說(shuō)明基金的單位風(fēng)險(xiǎn)所獲得的風(fēng)險(xiǎn)回報(bào)越高。夏普比率為負(fù)時(shí)，按大小排序沒(méi)有意義。[1] 夏普比率以資本市場(chǎng)線作為評(píng)價(jià)基準(zhǔn)，對(duì)投資績(jī)效作出評(píng)估。

3.利用Python分析6家公司股票（阿里巴巴 亞馬遜 騰訊 蘋(píng)果 facebook 谷歌）

首先導(dǎo)入包

創(chuàng)建字典

獲取阿里巴巴股票數(shù)據(jù)

會(huì)得到如下股票數(shù)據(jù)：

查看數(shù)據(jù)集描述

會(huì)得到下面的數(shù)據(jù)：

分析漲跌得到如下數(shù)據(jù)：

繪圖步驟

可以得到‘阿里巴巴’的股票走向

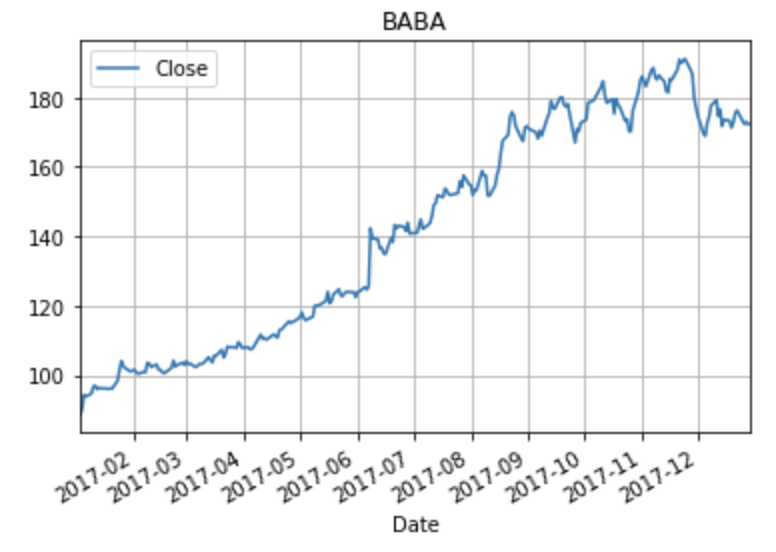
其他幾家公司同理：