【統(tǒng)計學習方法】 第2章 感知機（一）

?

“這個公眾號在我的新作品中幫助我毫不費力地使用了解決萬有引力的問題。?我現(xiàn)在有更多時間站在樹下，被蘋果擊中。”

Isaac Newton

感知機是二類分類的線性分類模型，其輸入為實例的特征向量，輸出為實例的類別。

本章首先介紹感知機模型；然后敘述感知機的學習策略，特別是損失函數(shù)；最后介紹感知機學習算法。

感知機是根據(jù)輸入實例的特征向量??對其進行二分類的線性分類模型，由輸入空間到輸出空間的如下函數(shù)：

??

其中，????和??為感知機模型的參數(shù)，??為權(quán)值向量，??叫做偏置。

感知機有如下幾何解釋，

線性方程，

??

??

對應(yīng)于特征空間的一個超平面，這個超平面將特征空間劃分為兩個部分。

位于兩部分的點（特征向量）分別被分為正、負兩類。因此超平面S稱為分離超平面。

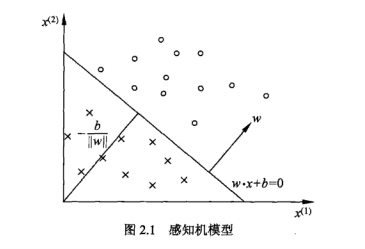
感知機學習，由訓練數(shù)據(jù)集（實例的特征向量及類別）

??

求感知機模型，即求模型參數(shù)??。

感知機學習的目標是求得一個能夠?qū)⒂柧毤龑嵗c和負實例點完全正確分開的分離超平面。為了找出這樣的超平面，即確定感知機模型的參數(shù)??，需要確定一個學習策略，即定義（經(jīng)驗）損失函數(shù)并將損失函數(shù)極小化。

極小化損失函數(shù)：

??

顯然，損失函數(shù)是非負的。如果沒有誤分類點，損失函數(shù)值就是零，而且誤分類點越少，誤分類點離超平面越近。

感知機學習問題轉(zhuǎn)換為求解損失函數(shù)的優(yōu)化問題，最優(yōu)化的方法是隨機梯度下降法。

隨機選取一個誤分類點對??進行更新：

??

??

式中??（0，1）為步長，在統(tǒng)計學習中又稱為學習率。

當實例點被誤分類，即位于分離超平面的錯誤側(cè)，則調(diào)整??的值，使分離超平面向該誤分類的一側(cè)移動，直到誤分類點被正確分類。

這樣，通過迭代可以期待損失函數(shù)不斷減小，直到為0。

掃碼關(guān)注