国产91久久婷婷一区二区,欧美一区二区三区的,日本免费看黄,国产 —一级a毛一级a看免费,蜜桃精品av久久久久久,亚洲AV五月天草榴,国产精品99久久久久久猫咪,日P视频网站

本文主要介紹基于集成學(xué)習(xí)的決策樹(shù)算法，通過(guò)學(xué)習(xí)得到的的決策樹(shù)基學(xué)習(xí)器，并綜合所有基學(xué)習(xí)器的預(yù)測(cè)結(jié)果來(lái)改善單個(gè)基學(xué)習(xí)器的識(shí)別率和泛化性。

集成學(xué)習(xí)

常見(jiàn)的集成學(xué)習(xí)框架有三種：Bagging，Boosting 和 Stacking。三種集成學(xué)習(xí)框架在基學(xué)習(xí)器的產(chǎn)生和綜合結(jié)果的方式上會(huì)有些區(qū)別，我們先做些簡(jiǎn)單的介紹。

1.1 Bagging

Bagging 全稱叫 Bootstrap aggregating，看到 Bootstrap 我們立刻想到著名的開(kāi)源前端框架（抖個(gè)機(jī)靈，是 Bootstrap 抽樣方法），每個(gè)基學(xué)習(xí)器都會(huì)對(duì)訓(xùn)練集進(jìn)行有放回抽樣得到子訓(xùn)練集，比較著名的采樣法為 0.632 自助法。每個(gè)基學(xué)習(xí)器基于不同子訓(xùn)練集進(jìn)行訓(xùn)練，并綜合所有基學(xué)習(xí)器的預(yù)測(cè)值得到最終的預(yù)測(cè)結(jié)果。Bagging 常用的綜合方法是投票法，票數(shù)最多的類別為預(yù)測(cè)類別。

1.2 Boosting

Boosting 訓(xùn)練過(guò)程為階梯狀，基模型的訓(xùn)練是有順序的，每個(gè)基模型都會(huì)在前一個(gè)基模型學(xué)習(xí)的基礎(chǔ)上進(jìn)行學(xué)習(xí)，最終綜合所有基模型的預(yù)測(cè)值產(chǎn)生最終的預(yù)測(cè)結(jié)果，用的比較多的綜合方式為加權(quán)法。

1.3 Stacking

Stacking 是先用全部數(shù)據(jù)訓(xùn)練好基模型，然后每個(gè)基模型都對(duì)每個(gè)訓(xùn)練樣本進(jìn)行的預(yù)測(cè)，其預(yù)測(cè)值將作為訓(xùn)練樣本的特征值，最終會(huì)得到新的訓(xùn)練樣本，然后基于新的訓(xùn)練樣本進(jìn)行訓(xùn)練得到模型，然后得到最終預(yù)測(cè)結(jié)果。

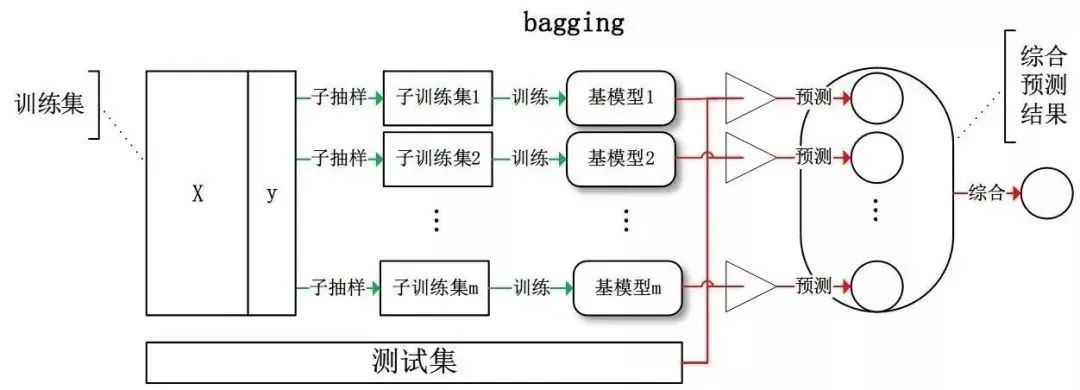
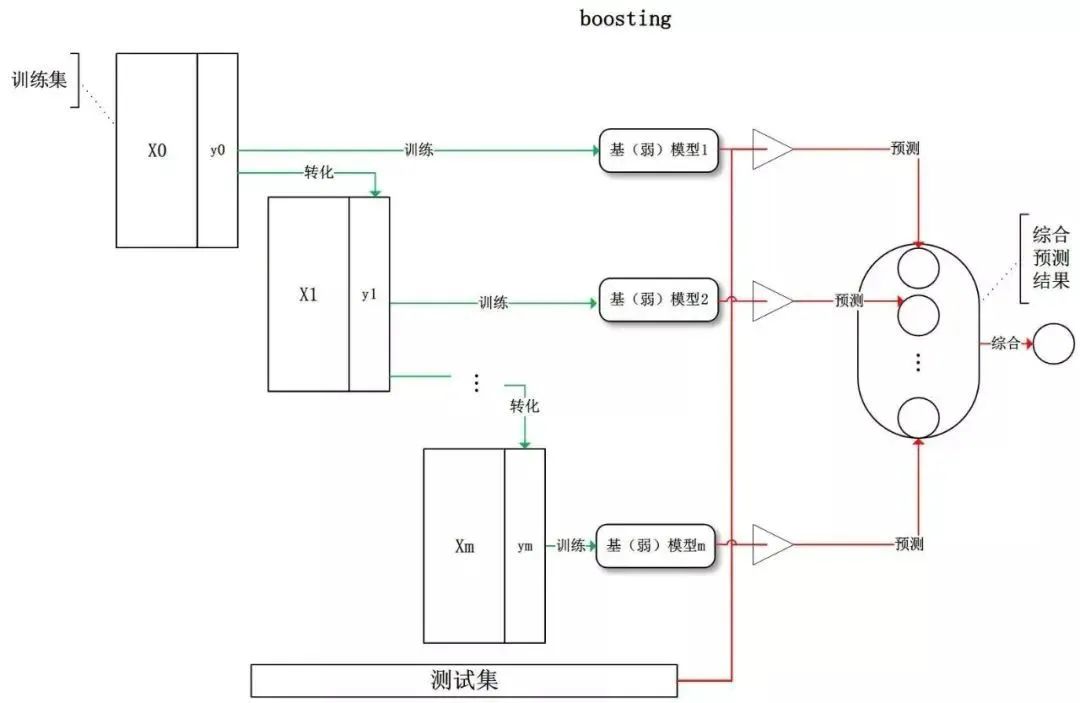
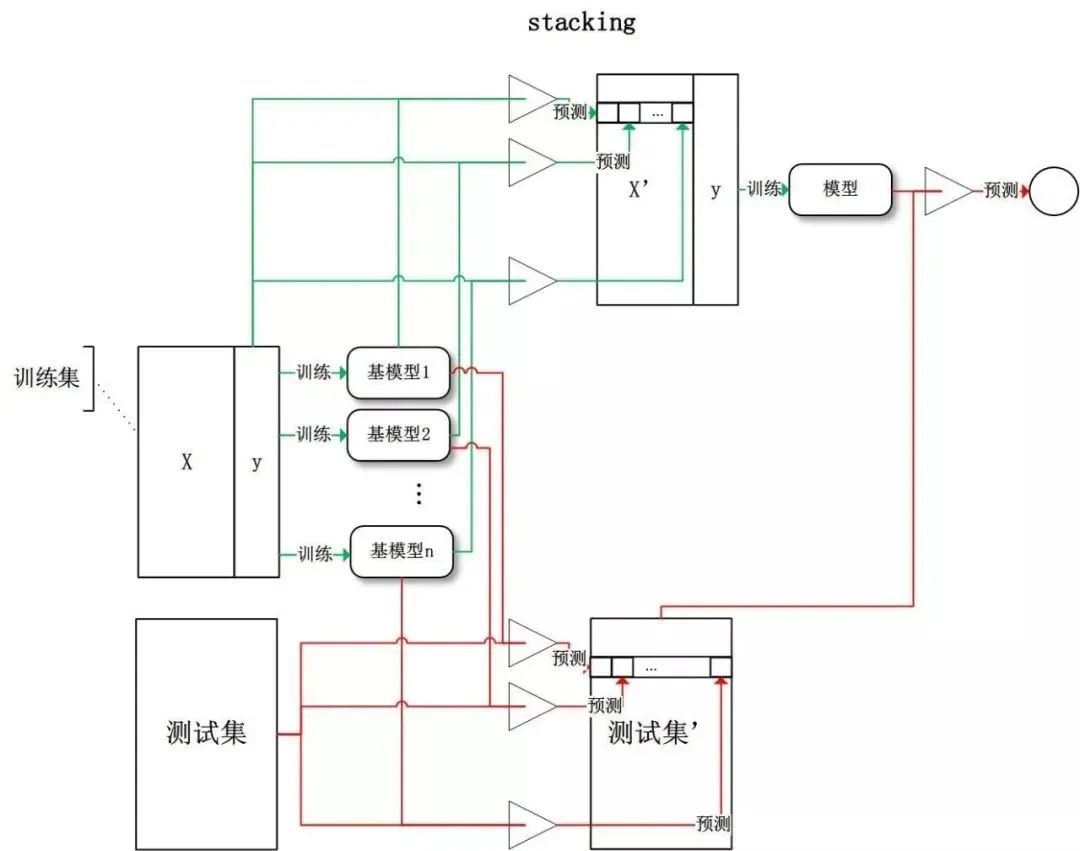
那么，為什么集成學(xué)習(xí)會(huì)好于單個(gè)學(xué)習(xí)器呢？原因可能有三：

訓(xùn)練樣本可能無(wú)法選擇出最好的單個(gè)學(xué)習(xí)器，由于沒(méi)法選擇出最好的學(xué)習(xí)器，所以干脆結(jié)合起來(lái)一起用；
假設(shè)能找到最好的學(xué)習(xí)器，但由于算法運(yùn)算的限制無(wú)法找到最優(yōu)解，只能找到次優(yōu)解，采用集成學(xué)習(xí)可以彌補(bǔ)算法的不足；
可能算法無(wú)法得到最優(yōu)解，而集成學(xué)習(xí)能夠得到近似解。比如說(shuō)最優(yōu)解是一條對(duì)角線，而單個(gè)決策樹(shù)得到的結(jié)果只能是平行于坐標(biāo)軸的，但是集成學(xué)習(xí)可以去擬合這條對(duì)角線。

偏差與方差

上節(jié)介紹了集成學(xué)習(xí)的基本概念，這節(jié)我們主要介紹下如何從偏差和方差的角度來(lái)理解集成學(xué)習(xí)。

2.1 集成學(xué)習(xí)的偏差與方差

偏差（Bias）描述的是預(yù)測(cè)值和真實(shí)值之差；方差（Variance）描述的是預(yù)測(cè)值作為隨機(jī)變量的離散程度。放一場(chǎng)很經(jīng)典的圖：

模型的偏差與方差

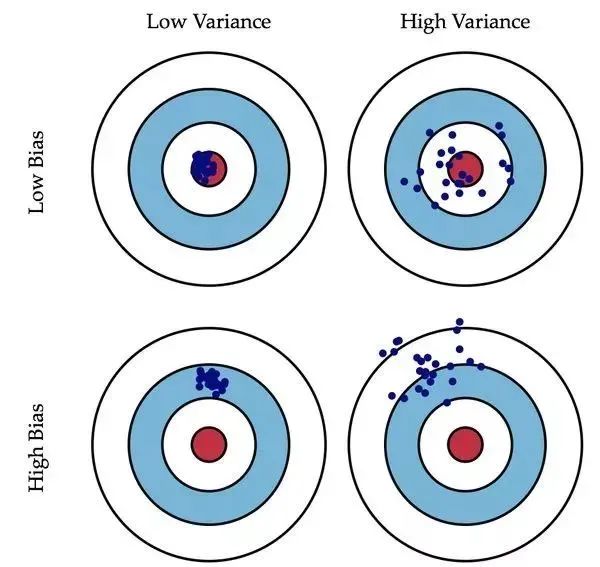
偏差：描述樣本擬合出的模型的預(yù)測(cè)結(jié)果的期望與樣本真實(shí)結(jié)果的差距，要想偏差表現(xiàn)的好，就需要復(fù)雜化模型，增加模型的參數(shù)，但這樣容易過(guò)擬合，過(guò)擬合對(duì)應(yīng)上圖的 High Variance，點(diǎn)會(huì)很分散。低偏差對(duì)應(yīng)的點(diǎn)都打在靶心附近，所以喵的很準(zhǔn)，但不一定很穩(wěn)；
方差：描述樣本上訓(xùn)練出來(lái)的模型在測(cè)試集上的表現(xiàn)，要想方差表現(xiàn)的好，需要簡(jiǎn)化模型，減少模型的復(fù)雜度，但這樣容易欠擬合，欠擬合對(duì)應(yīng)上圖 High Bias，點(diǎn)偏離中心。低方差對(duì)應(yīng)就是點(diǎn)都打的很集中，但不一定是靶心附近，手很穩(wěn)，但不一定瞄的準(zhǔn)。

我們常說(shuō)集成學(xué)習(xí)中的基模型是弱模型，通常來(lái)說(shuō)弱模型是偏差高（在訓(xùn)練集上準(zhǔn)確度低）方差小（防止過(guò)擬合能力強(qiáng)）的模型。但是，并不是所有集成學(xué)習(xí)框架中的基模型都是弱模型。Bagging 和 Stacking 中的基模型為強(qiáng)模型（偏差低方差高），Boosting 中的基模型為弱模型。

在 Bagging 和 Boosting 框架中，通過(guò)計(jì)算基模型的期望和方差我們可以得到模型整體的期望和方差。為了簡(jiǎn)化模型，我們假設(shè)基模型的權(quán)重?、方差??及兩兩間的相關(guān)系數(shù)??相等。由于 Bagging 和 Boosting 的基模型都是線性組成的，那么有：

模型總體期望：

模型總體方差：

2.2 Bagging 的偏差與方差

對(duì)于 Bagging 來(lái)說(shuō)，每個(gè)基模型的權(quán)重等于 1/m 且期望近似相等（子訓(xùn)練集都是從原訓(xùn)練集中進(jìn)行子抽樣），故我們可以進(jìn)一步化簡(jiǎn)得到：

通過(guò)上式我們可以看到

整體模型的期望等于基模型的期望，這也就意味著整體模型的偏差和基模型的偏差近似。
整體模型的方差小于等于基模型的方差，當(dāng)且僅當(dāng)相關(guān)性為 1 時(shí)取等號(hào)，隨著基模型數(shù)量增多，整體模型的方差減少，從而防止過(guò)擬合的能力增強(qiáng)，模型的準(zhǔn)確度得到提高。但是，模型的準(zhǔn)確度一定會(huì)無(wú)限逼近于 1 嗎？并不一定，當(dāng)基模型數(shù)增加到一定程度時(shí)，方差公式第一項(xiàng)的改變對(duì)整體方差的作用很小，防止過(guò)擬合的能力達(dá)到極限，這便是準(zhǔn)確度的極限了。

在此我們知道了為什么 Bagging 中的基模型一定要為強(qiáng)模型，如果 Bagging 使用弱模型則會(huì)導(dǎo)致整體模型的偏差提高，而準(zhǔn)確度降低。

Random Forest 是經(jīng)典的基于 Bagging 框架的模型，并在此基礎(chǔ)上通過(guò)引入特征采樣和樣本采樣來(lái)降低基模型間的相關(guān)性，在公式中顯著降低方差公式中的第二項(xiàng)，略微升高第一項(xiàng)，從而使得整體降低模型整體方差。

2.3 Boosting 的偏差與方差

對(duì)于 Boosting 來(lái)說(shuō)，基模型的訓(xùn)練集抽樣是強(qiáng)相關(guān)的，那么模型的相關(guān)系數(shù)近似等于 1，故我們也可以針對(duì) Boosting 化簡(jiǎn)公式為：

通過(guò)觀察整體方差的表達(dá)式我們?nèi)菀装l(fā)現(xiàn)：

整體模型的方差等于基模型的方差，如果基模型不是弱模型，其方差相對(duì)較大，這將導(dǎo)致整體模型的方差很大，即無(wú)法達(dá)到防止過(guò)擬合的效果。因此，Boosting 框架中的基模型必須為弱模型。
此外 Boosting 框架中采用基于貪心策略的前向加法，整體模型的期望由基模型的期望累加而成，所以隨著基模型數(shù)的增多，整體模型的期望值增加，整體模型的準(zhǔn)確度提高。

基于 Boosting 框架的 Gradient Boosting Decision Tree 模型中基模型也為樹(shù)模型，同 Random Forrest，我們也可以對(duì)特征進(jìn)行隨機(jī)抽樣來(lái)使基模型間的相關(guān)性降低，從而達(dá)到減少方差的效果。

2.4 小結(jié)

我們可以使用模型的偏差和方差來(lái)近似描述模型的準(zhǔn)確度；
對(duì)于 Bagging 來(lái)說(shuō)，整體模型的偏差與基模型近似，而隨著模型的增加可以降低整體模型的方差，故其基模型需要為強(qiáng)模型；
對(duì)于 Boosting 來(lái)說(shuō)，整體模型的方差近似等于基模型的方差，而整體模型的偏差由基模型累加而成，故基模型需要為弱模型。

Random Forest

Random Forest（隨機(jī)森林），用隨機(jī)的方式建立一個(gè)森林。RF 算法由很多決策樹(shù)組成，每一棵決策樹(shù)之間沒(méi)有關(guān)聯(lián)。建立完森林后，當(dāng)有新樣本進(jìn)入時(shí)，每棵決策樹(shù)都會(huì)分別進(jìn)行判斷，然后基于投票法給出分類結(jié)果。

3.1 思想

Random Forest（隨機(jī)森林）是 Bagging 的擴(kuò)展變體，它在以決策樹(shù)為基學(xué)習(xí)器構(gòu)建 Bagging 集成的基礎(chǔ)上，進(jìn)一步在決策樹(shù)的訓(xùn)練過(guò)程中引入了隨機(jī)特征選擇，因此可以概括 RF 包括四個(gè)部分：

隨機(jī)選擇樣本（放回抽樣）；
隨機(jī)選擇特征；
構(gòu)建決策樹(shù)；
隨機(jī)森林投票（平均）。

隨機(jī)選擇樣本和 Bagging 相同，采用的是 Bootstrap 自助采樣法；隨機(jī)選擇特征是指在每個(gè)節(jié)點(diǎn)在分裂過(guò)程中都是隨機(jī)選擇特征的（區(qū)別與每棵樹(shù)隨機(jī)選擇一批特征）。

這種隨機(jī)性導(dǎo)致隨機(jī)森林的偏差會(huì)有稍微的增加（相比于單棵不隨機(jī)樹(shù)），但是由于隨機(jī)森林的“平均”特性，會(huì)使得它的方差減小，而且方差的減小補(bǔ)償了偏差的增大，因此總體而言是更好的模型。

隨機(jī)采樣由于引入了兩種采樣方法保證了隨機(jī)性，所以每棵樹(shù)都是最大可能的進(jìn)行生長(zhǎng)就算不剪枝也不會(huì)出現(xiàn)過(guò)擬合。

3.2 優(yōu)缺點(diǎn)

優(yōu)點(diǎn)

在數(shù)據(jù)集上表現(xiàn)良好，相對(duì)于其他算法有較大的優(yōu)勢(shì)
易于并行化，在大數(shù)據(jù)集上有很大的優(yōu)勢(shì)；
能夠處理高維度數(shù)據(jù)，不用做特征選擇。

AdaBoost

AdaBoost（Adaptive Boosting，自適應(yīng)增強(qiáng)），其自適應(yīng)在于：前一個(gè)基本分類器分錯(cuò)的樣本會(huì)得到加強(qiáng)，加權(quán)后的全體樣本再次被用來(lái)訓(xùn)練下一個(gè)基本分類器。同時(shí)，在每一輪中加入一個(gè)新的弱分類器，直到達(dá)到某個(gè)預(yù)定的足夠小的錯(cuò)誤率或達(dá)到預(yù)先指定的最大迭代次數(shù)。

4.1 思想

Adaboost 迭代算法有三步：

初始化訓(xùn)練樣本的權(quán)值分布，每個(gè)樣本具有相同權(quán)重；
訓(xùn)練弱分類器，如果樣本分類正確，則在構(gòu)造下一個(gè)訓(xùn)練集中，它的權(quán)值就會(huì)被降低；反之提高。用更新過(guò)的樣本集去訓(xùn)練下一個(gè)分類器；
將所有弱分類組合成強(qiáng)分類器，各個(gè)弱分類器的訓(xùn)練過(guò)程結(jié)束后，加大分類誤差率小的弱分類器的權(quán)重，降低分類誤差率大的弱分類器的權(quán)重。

4.2 細(xì)節(jié)

4.2.1 損失函數(shù)

Adaboost 模型是加法模型，學(xué)習(xí)算法為前向分步學(xué)習(xí)算法，損失函數(shù)為指數(shù)函數(shù)的分類問(wèn)題。

加法模型：最終的強(qiáng)分類器是由若干個(gè)弱分類器加權(quán)平均得到的。

前向分布學(xué)習(xí)算法：算法是通過(guò)一輪輪的弱學(xué)習(xí)器學(xué)習(xí)，利用前一個(gè)弱學(xué)習(xí)器的結(jié)果來(lái)更新后一個(gè)弱學(xué)習(xí)器的訓(xùn)練集權(quán)重。第 k 輪的強(qiáng)學(xué)習(xí)器為：

損失函數(shù)：

利用前向分布學(xué)習(xí)算法的關(guān)系可以得到損失函數(shù)為：

令?

，它的值不依賴于?，因此與最小化無(wú)關(guān)，僅僅依賴于?，隨著每一輪迭代而將這個(gè)式子帶入損失函數(shù)，損失函數(shù)轉(zhuǎn)化為：

我們求?，可以得到：

將??帶入損失函數(shù)，并對(duì) \alpha 求導(dǎo)，使其等于 0，則就得到了：

其中，?即為我們前面的分類誤差率。

最后看樣本權(quán)重的更新。利用?

?和?

，即可得：

這樣就得到了樣本權(quán)重更新公式。

4.2.2 正則化

為了防止 Adaboost 過(guò)擬合，我們通常也會(huì)加入正則化項(xiàng)，這個(gè)正則化項(xiàng)我們通常稱為步長(zhǎng)（learning rate）。定義為 v，對(duì)于前面的弱學(xué)習(xí)器的迭代

加上正則化我們有：

v 的取值范圍為 0v1。對(duì)于同樣的訓(xùn)練集學(xué)習(xí)效果，較小的 v 意味著我們需要更多的弱學(xué)習(xí)器的迭代次數(shù)。通常我們用步長(zhǎng)和迭代最大次數(shù)一起來(lái)決定算法的擬合效果。

4.3 優(yōu)缺點(diǎn)

優(yōu)點(diǎn)

分類精度高；
可以用各種回歸分類模型來(lái)構(gòu)建弱學(xué)習(xí)器，非常靈活；
不容易發(fā)生過(guò)擬合。

缺點(diǎn)

對(duì)異常點(diǎn)敏感，異常點(diǎn)會(huì)獲得較高權(quán)重。

GBDT

GBDT（Gradient Boosting Decision Tree）是一種迭代的決策樹(shù)算法，該算法由多棵決策樹(shù)組成，從名字中我們可以看出來(lái)它是屬于 Boosting 策略。GBDT 是被公認(rèn)的泛化能力較強(qiáng)的算法。編者注：像LightGBM、XGBOOST等競(jìng)賽神器就是基于GBDT再做優(yōu)化實(shí)現(xiàn)的。

5.1 思想

GBDT 由三個(gè)概念組成：Regression Decision Tree（即 DT）、Gradient Boosting（即 GB），和SHringkage（一個(gè)重要演變）

5.1.1 回歸樹(shù)（Regression Decision Tree）

如果認(rèn)為 GBDT 由很多分類樹(shù)那就大錯(cuò)特錯(cuò)了（雖然調(diào)整后也可以分類）。對(duì)于分類樹(shù)而言，其值加減無(wú)意義（如性別），而對(duì)于回歸樹(shù)而言，其值加減才是有意義的（如說(shuō)年齡）。GBDT 的核心在于累加所有樹(shù)的結(jié)果作為最終結(jié)果，所以 GBDT 中的樹(shù)都是回歸樹(shù)，不是分類樹(shù)，這一點(diǎn)相當(dāng)重要。

回歸樹(shù)在分枝時(shí)會(huì)窮舉每一個(gè)特征的每個(gè)閾值以找到最好的分割點(diǎn)，衡量標(biāo)準(zhǔn)是最小化均方誤差。

5.1.2 梯度迭代（Gradient Boosting）

上面說(shuō)到 GBDT 的核心在于累加所有樹(shù)的結(jié)果作為最終結(jié)果，GBDT 的每一棵樹(shù)都是以之前樹(shù)得到的殘差來(lái)更新目標(biāo)值，這樣每一棵樹(shù)的值加起來(lái)即為 GBDT 的預(yù)測(cè)值。

模型的預(yù)測(cè)值可以表示為：

?為基模型與其權(quán)重的乘積，模型的訓(xùn)練目標(biāo)是使預(yù)測(cè)值??逼近真實(shí)值?，也就是說(shuō)要讓每個(gè)基模型的預(yù)測(cè)值逼近各自要預(yù)測(cè)的部分真實(shí)值。由于要同時(shí)考慮所有基模型，導(dǎo)致了整體模型的訓(xùn)練變成了一個(gè)非常復(fù)雜的問(wèn)題。所以研究者們想到了一個(gè)貪心的解決手段：每次只訓(xùn)練一個(gè)基模型。那么，現(xiàn)在改寫(xiě)整體模型為迭代式：

這樣一來(lái)，每一輪迭代中，只要集中解決一個(gè)基模型的訓(xùn)練問(wèn)題：使 F_i(x) 逼近真實(shí)值 y。

舉個(gè)例子：比如說(shuō) A 用戶年齡 20 歲，第一棵樹(shù)預(yù)測(cè) 12 歲，那么殘差就是 8，第二棵樹(shù)用 8 來(lái)學(xué)習(xí)，假設(shè)其預(yù)測(cè)為 5，那么其殘差即為 3，如此繼續(xù)學(xué)習(xí)即可。

那么 Gradient 從何體現(xiàn)？其實(shí)很簡(jiǎn)單，其殘差其實(shí)是最小均方損失函數(shù)關(guān)于預(yù)測(cè)值的反向梯度：

也就是說(shuō)，若??加上擬合了反向梯度的??得到?，該值可能將導(dǎo)致平方差損失函數(shù)降低，預(yù)測(cè)的準(zhǔn)確度提高！

但要注意，基于殘差 GBDT 容易對(duì)異常值敏感，舉例：

很明顯后續(xù)的模型會(huì)對(duì)第 4 個(gè)值關(guān)注過(guò)多，這不是一種好的現(xiàn)象，所以一般回歸類的損失函數(shù)會(huì)用絕對(duì)損失或者 Huber 損失函數(shù)來(lái)代替平方損失函數(shù)。

GBDT 的 Boosting 不同于 Adaboost 的 Boosting，GBDT 的每一步殘差計(jì)算其實(shí)變相地增大了被分錯(cuò)樣本的權(quán)重，而對(duì)與分對(duì)樣本的權(quán)重趨于 0，這樣后面的樹(shù)就能專注于那些被分錯(cuò)的樣本。

5.1.13 縮減（Shrinkage）

Shrinkage 的思想認(rèn)為，每走一小步逐漸逼近結(jié)果的效果要比每次邁一大步很快逼近結(jié)果的方式更容易避免過(guò)擬合。即它并不是完全信任每一棵殘差樹(shù)。

, ?(0v1)

Shrinkage 不直接用殘差修復(fù)誤差，而是只修復(fù)一點(diǎn)點(diǎn)，把大步切成小步。本質(zhì)上 Shrinkage 為每棵樹(shù)設(shè)置了一個(gè) weight，累加時(shí)要乘以這個(gè) weight，當(dāng) weight 降低時(shí)，基模型數(shù)會(huì)配合增大。

5.2 優(yōu)缺點(diǎn)

優(yōu)點(diǎn)

可以自動(dòng)進(jìn)行特征組合，擬合非線性數(shù)據(jù)；
可以靈活處理各種類型的數(shù)據(jù)。

缺點(diǎn)

對(duì)異常點(diǎn)敏感。

5.3 與 Adaboost 的對(duì)比

相同：

都是 Boosting 家族成員，使用弱分類器；
都使用前向分布算法；

不同：

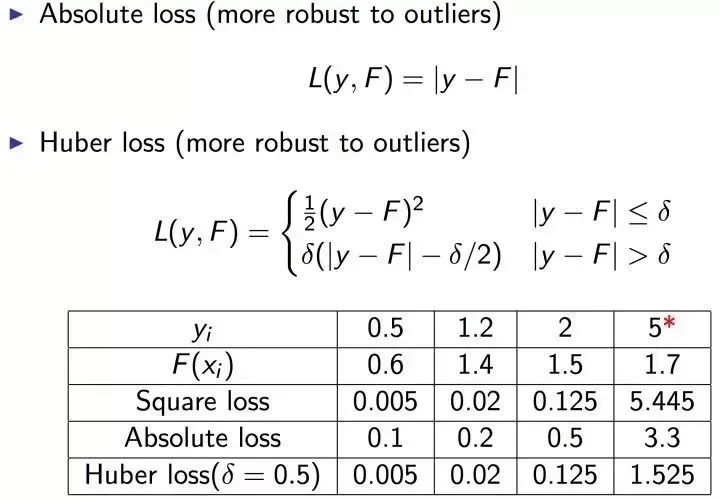
迭代思路不同：Adaboost 是通過(guò)提升錯(cuò)分?jǐn)?shù)據(jù)點(diǎn)的權(quán)重來(lái)彌補(bǔ)模型的不足（利用錯(cuò)分樣本），而 GBDT 是通過(guò)算梯度來(lái)彌補(bǔ)模型的不足（利用殘差）；
損失函數(shù)不同：AdaBoost 采用的是指數(shù)損失，GBDT 使用的是絕對(duì)損失或者 Huber 損失函數(shù)；

3種常見(jiàn)的集成學(xué)習(xí)決策樹(shù)算法及原理

2.1 集成學(xué)習(xí)的偏差與方差