如何 Get 機(jī)器學(xué)習(xí)必備的數(shù)學(xué)技能?(文末贈書)
1
數(shù)學(xué)對機(jī)器學(xué)習(xí)與深度學(xué)習(xí)的重要性
數(shù)學(xué)。這兩本書里密集的出現(xiàn)數(shù)學(xué)概念和公式,對大部分讀者來說都是很困難的,尤其是不少數(shù)學(xué)知識超出了理工科本科“微積分”,“線性代數(shù)”,“概率論與數(shù)理統(tǒng)計(jì)”3門課的范圍。陌生的數(shù)學(xué)符號和公式讓大家茫然不知所措。 機(jī)器學(xué)習(xí)和深度學(xué)習(xí)中的一些思想不易理解。有些復(fù)雜的算法,比如支持向量機(jī)、反向傳播算法、EM算法、概率圖模型、變分推斷,它們到底解決了什么問題,為什么要這樣做,這些書里解釋的不太清楚,這就造成了讀者不知其所以然。 抽象。有些機(jī)器學(xué)習(xí)算法是很抽象的,比如流形學(xué)習(xí)、譜聚類算法等。如果不給出直觀的解釋,也是難以理解的。 不能和應(yīng)用結(jié)合。很多教材普遍存在的一個(gè)問題是沒有講清楚這個(gè)方法到底有什么用,應(yīng)該怎么用。
2
西瓜書中的數(shù)學(xué)
最優(yōu)化方法
信息論
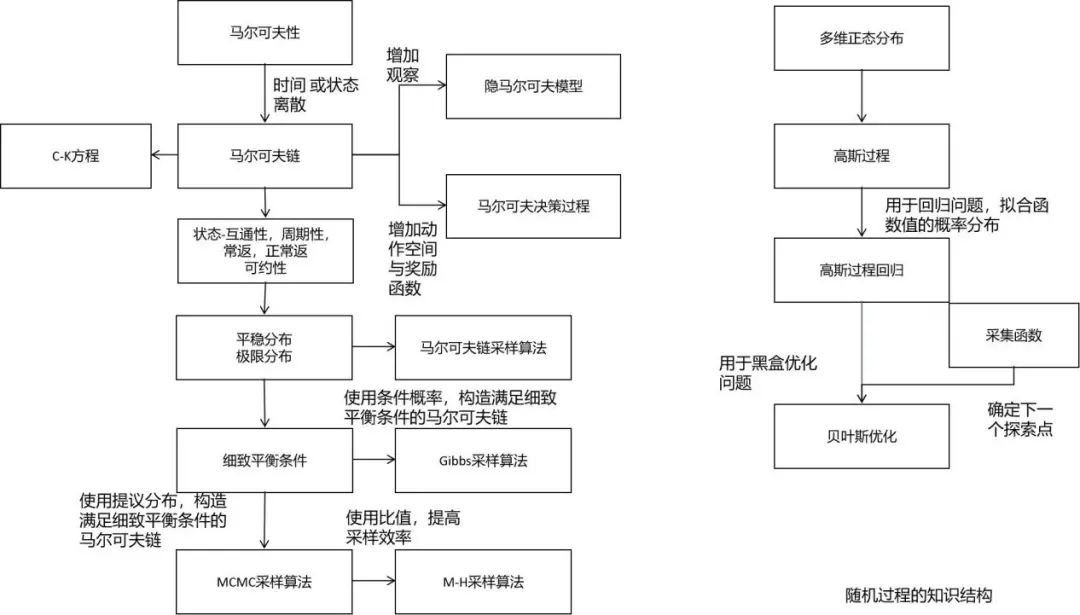
隨機(jī)過程
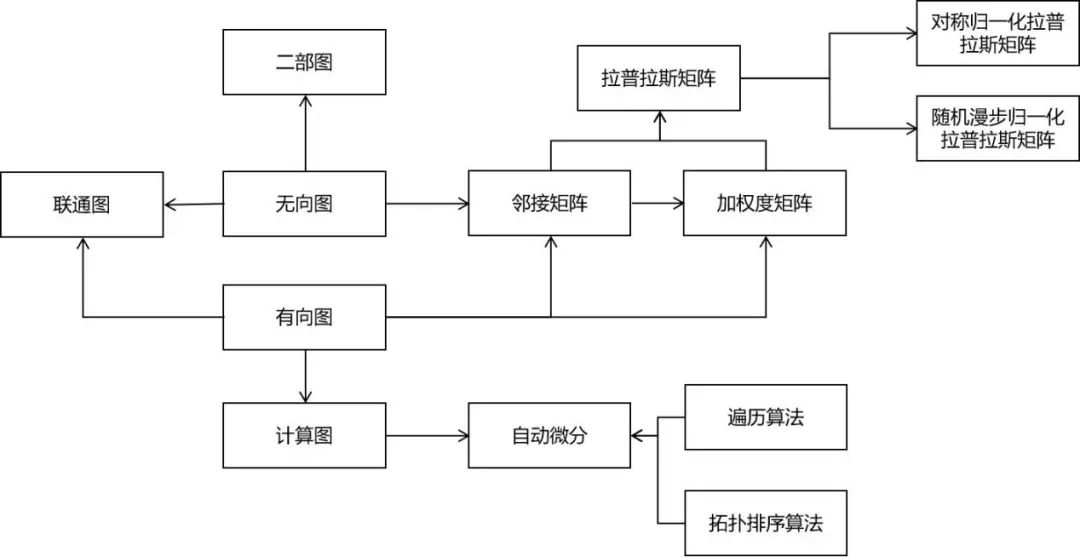
圖論
3
花書中的數(shù)學(xué)
線性代數(shù)
概率論與信息論
數(shù)值計(jì)算
線性因子模型
自編碼器
表示學(xué)習(xí)
深度學(xué)習(xí)中的結(jié)構(gòu)化概率模型
蒙特卡洛方法
直面配分函數(shù)
近似推斷
深度生成模型
MCMC采樣算法;
EM算法;
近似推斷和變分推斷;
變分法;
RBM的訓(xùn)練算法
最優(yōu)化方法
信息論
隨機(jī)過程
圖論

4
究竟需要哪些數(shù)學(xué)知識
微積分
線性代數(shù)
概率論
最優(yōu)化方法
信息論
隨機(jī)過程
圖論
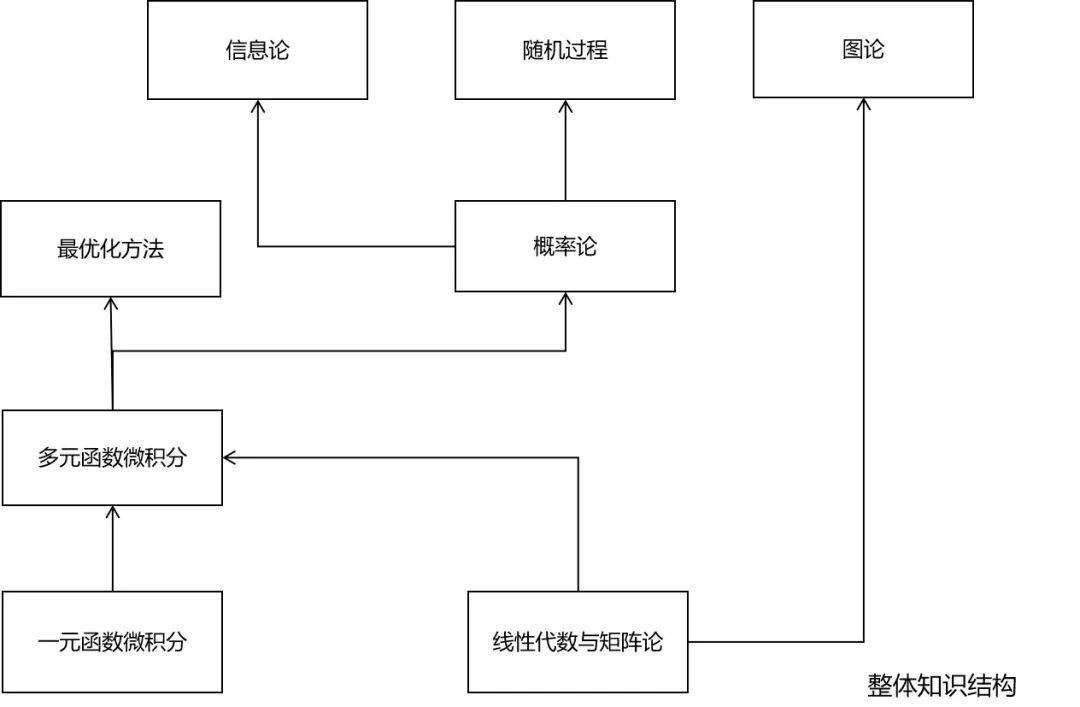
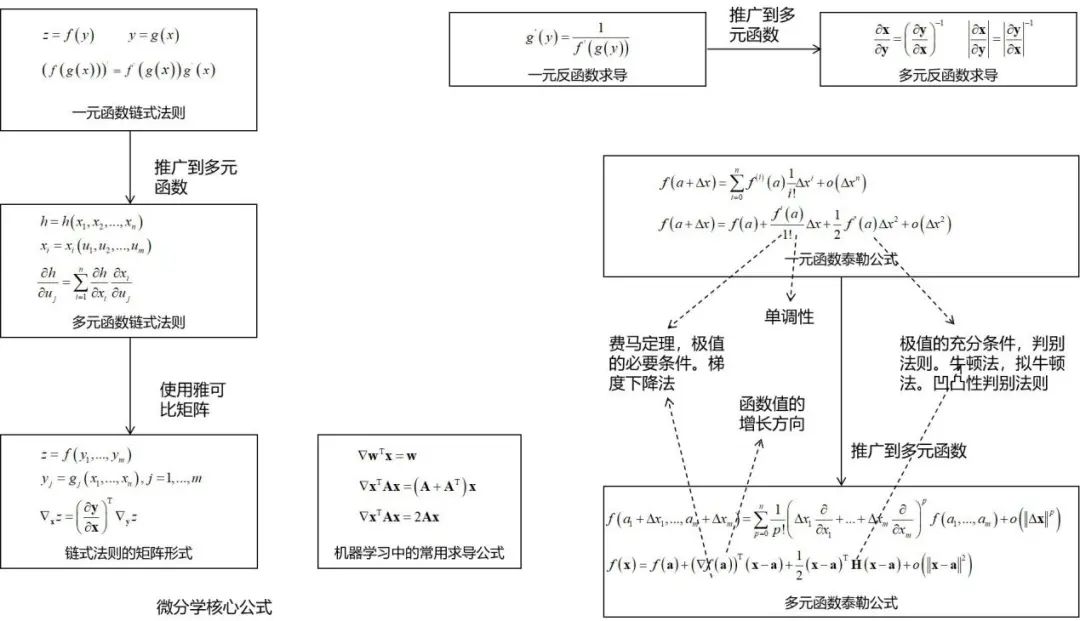
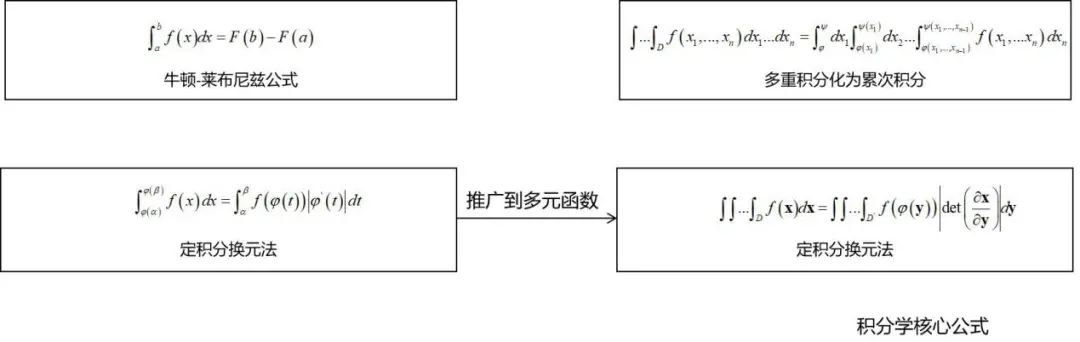
微積分
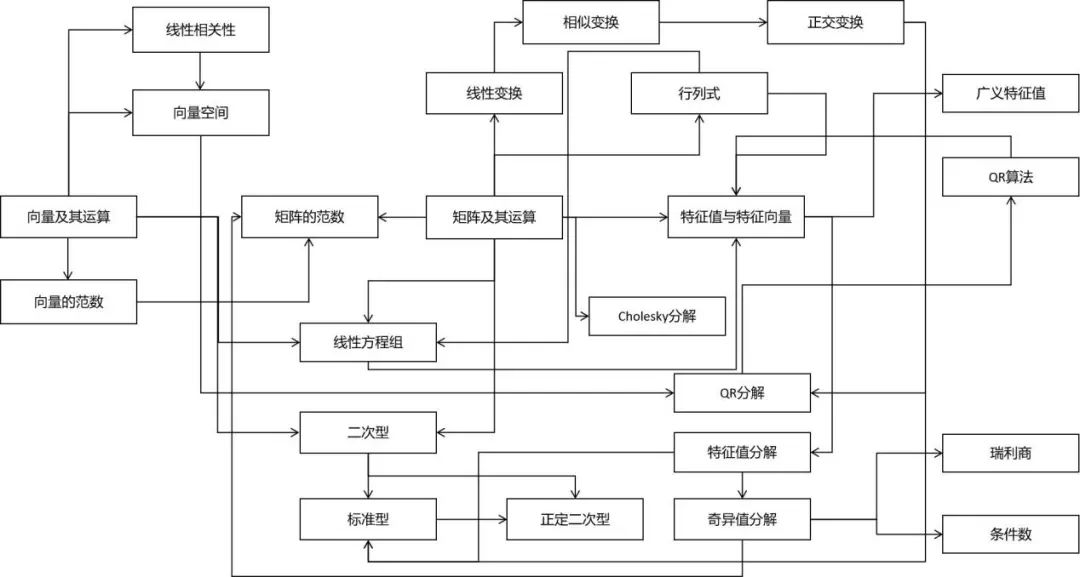
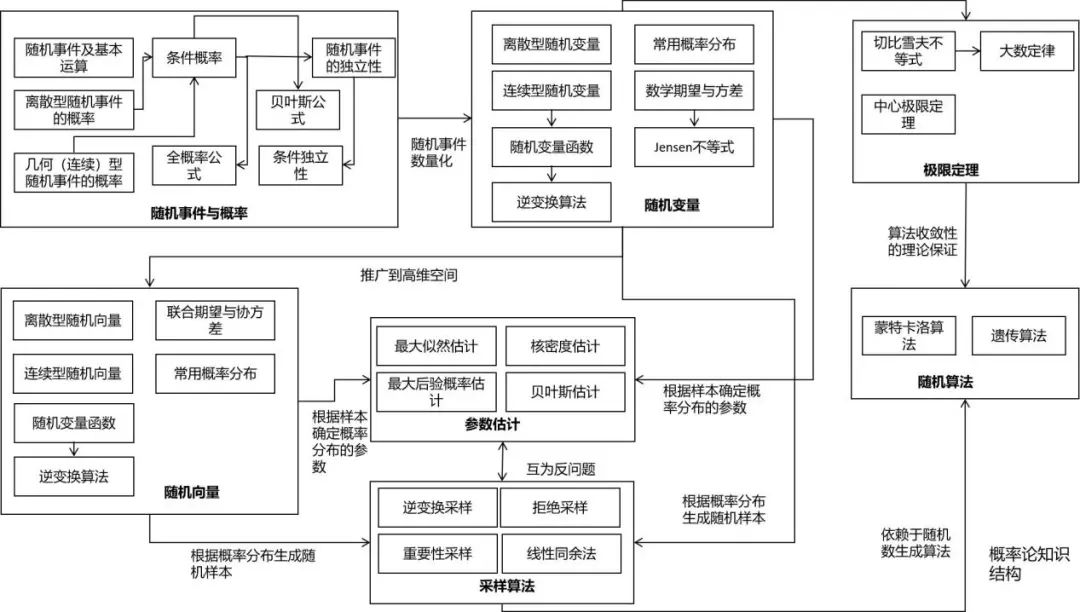
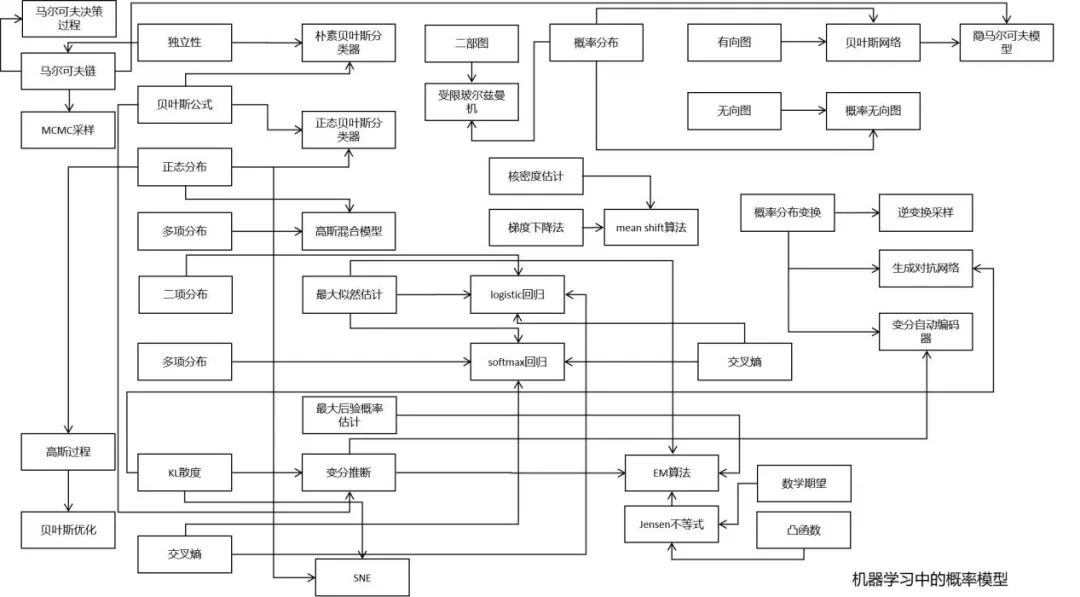
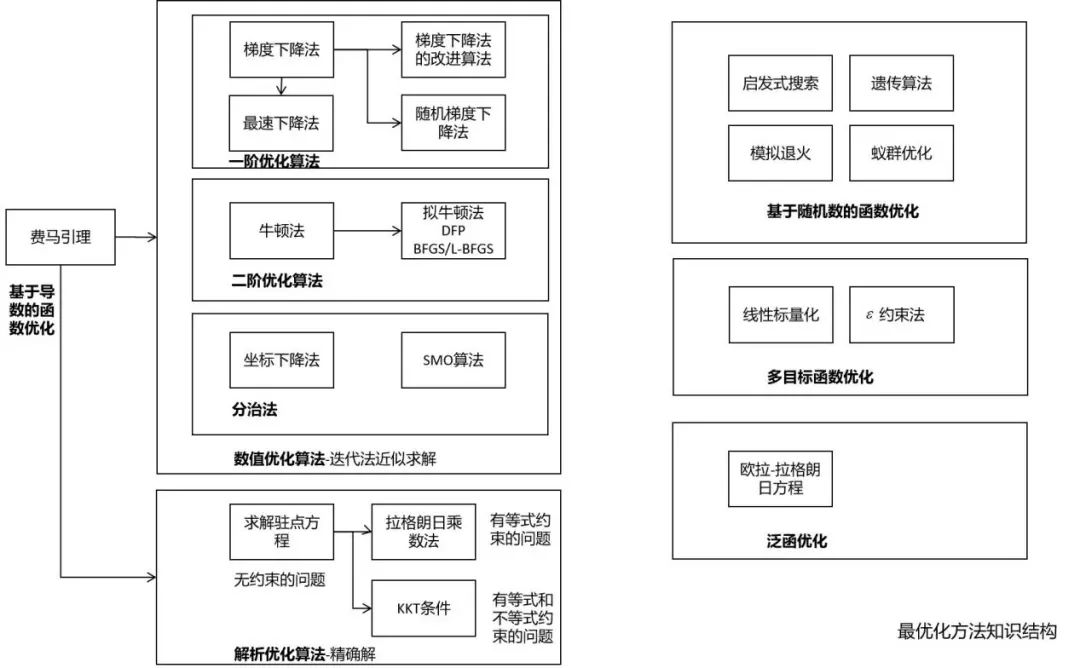
決策樹的訓(xùn)練過程中需要使用熵作為指標(biāo) 在深度學(xué)習(xí)中經(jīng)常會使用交叉熵、KL散度、JS散度、互信息等概念 變分推斷的推導(dǎo)需要以KL散度為基礎(chǔ) 距離度量學(xué)習(xí)、流形降維等算法也需要信息論的知識
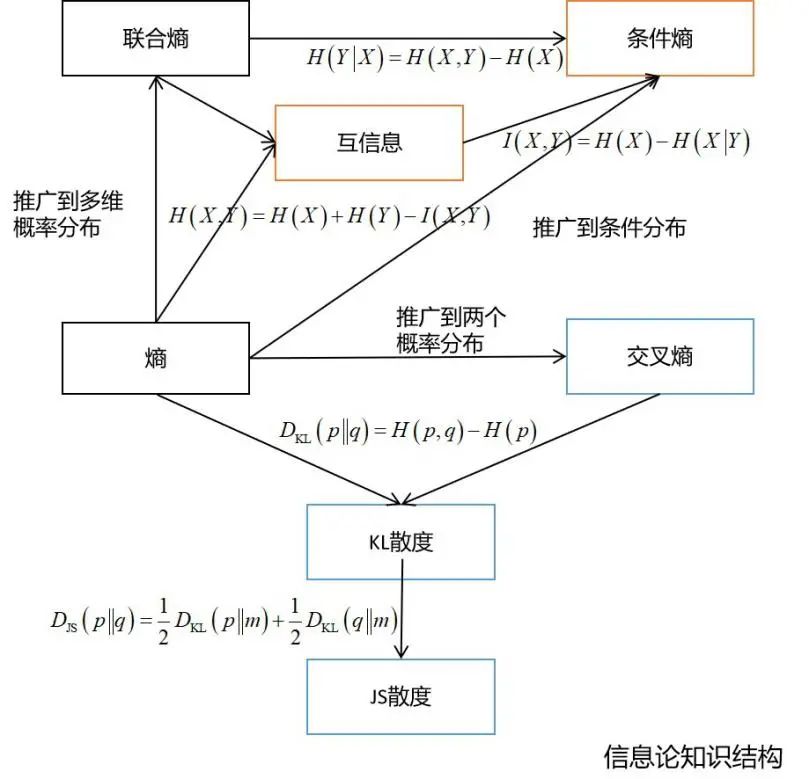
4
《機(jī)器學(xué)習(xí)的數(shù)學(xué)》是你的一個(gè)好選擇
使用圖/表等方式降低理解難度。
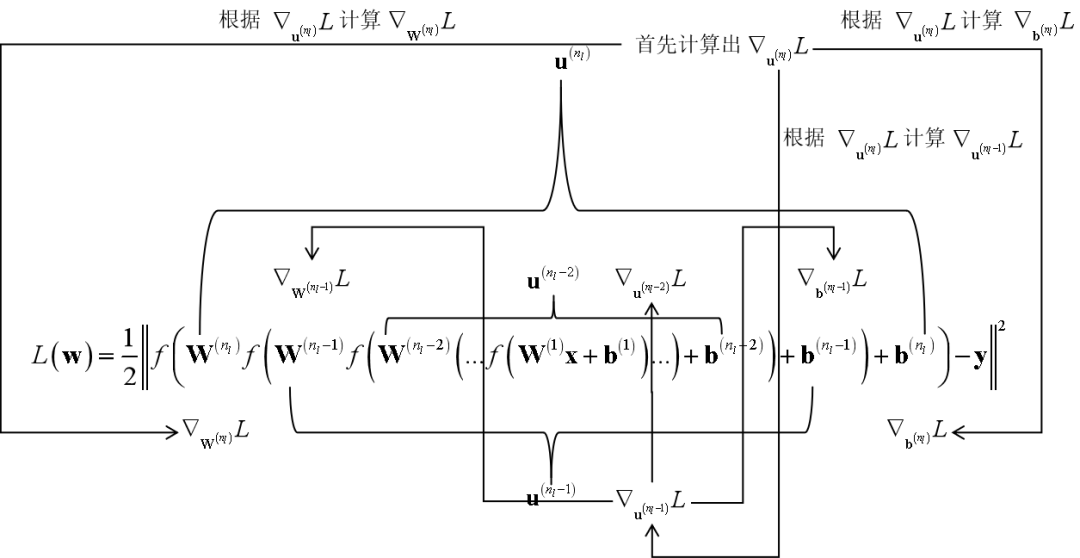
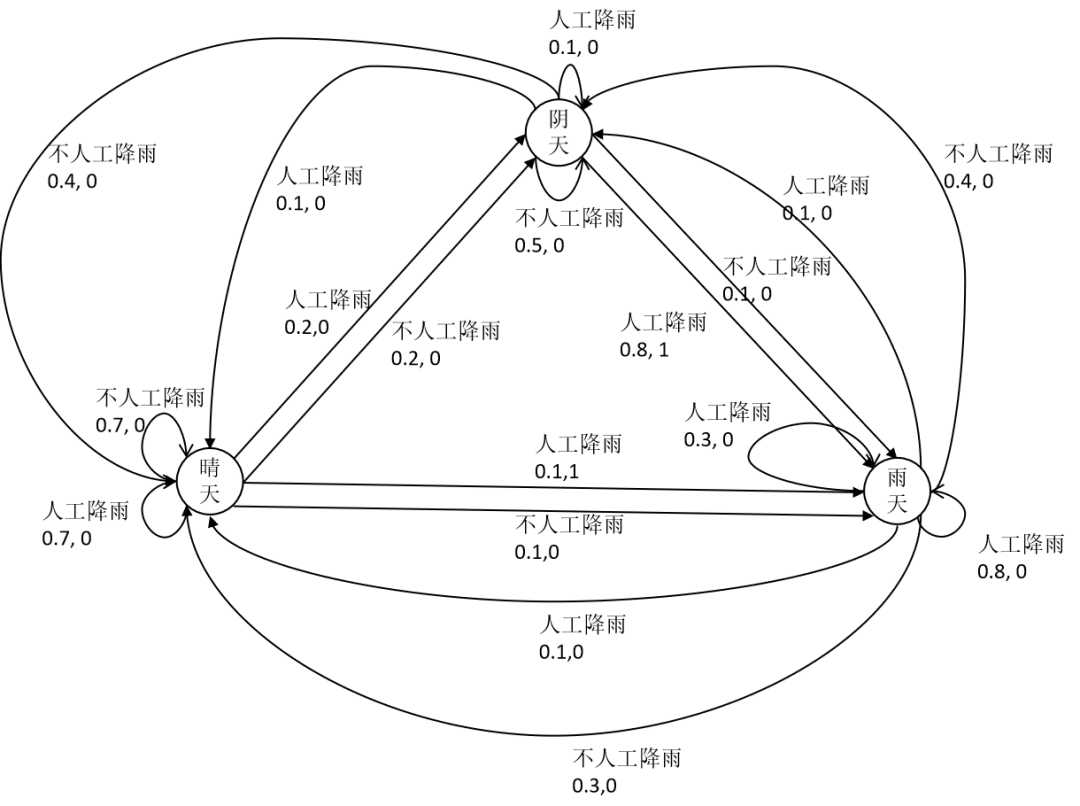
強(qiáng)化學(xué)習(xí)中為什么需要用馬爾可夫決策過程進(jìn)行建模? 為什么需要用狀態(tài)轉(zhuǎn)移概率? 為什么獎(jiǎng)勵(lì)函數(shù)與狀態(tài)轉(zhuǎn)移有關(guān)? 確定性策略,非確定性策略到底是怎么回事?
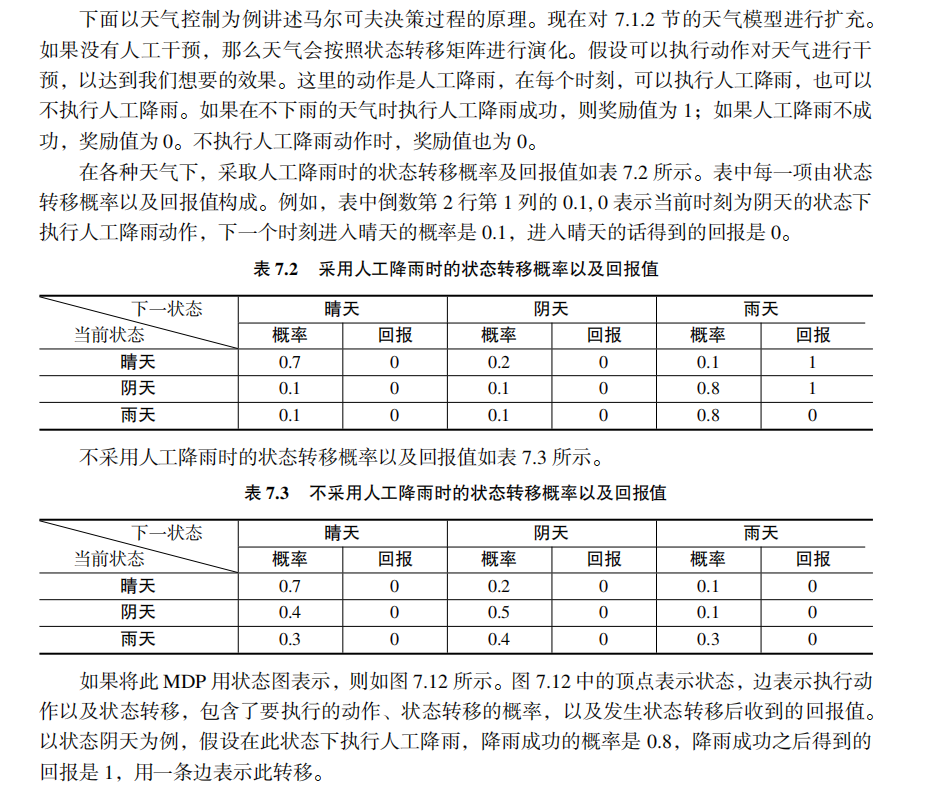
為什么用Householder變換可以將矩陣變換為近似對角的矩陣? Householder變換的變換矩陣是怎樣構(gòu)造的,為什么要這么構(gòu)造? 為何不直接將對稱矩陣變換為對角矩陣?


4
配套的高質(zhì)量課程
分享
收藏
點(diǎn)贊
在看

評論
圖片
表情
