正態(tài)分布（Normal distribution），也稱“常態(tài)分布”，又名高斯分布（Gaussian distribution），最早由A.棣莫弗在求二項分布的漸近公式中得到。C.F.高斯在研究測量誤差時從另一個角度導(dǎo)出了它。P.S.拉普拉斯和高斯研究了它的性質(zhì)。是一個在數(shù)學(xué)、物理及工程等領(lǐng)域都非常重要的概率分布，在統(tǒng)計學(xué)的許多方面有著重大的影響力。

正態(tài)曲線呈鐘型，兩頭低，中間高，左右對稱因其曲線呈鐘形，因此人們又經(jīng)常稱之為鐘形曲線。

正太性檢驗

利用觀測數(shù)據(jù)判斷總體是否服從正態(tài)分布的檢驗稱為正態(tài)性檢驗，它是統(tǒng)計判決中重要的一種特殊的擬合優(yōu)度假設(shè)檢驗。

直方圖初判 / QQ圖判斷 / K-S檢驗

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
% matplotlib inline

直方圖初判

s = pd.DataFrame(np.random.randn(1000)+10,columns = ['value'])
print(s.head())
# 創(chuàng)建隨機數(shù)據(jù)

fig = plt.figure(figsize = (10,6))
ax1 = fig.add_subplot(2,1,1)  # 創(chuàng)建子圖1
ax1.scatter(s.index, s.values)
plt.grid()
# 繪制數(shù)據(jù)分布圖

ax2 = fig.add_subplot(2,1,2)  # 創(chuàng)建子圖2
s.hist(bins=30,alpha = 0.5,ax = ax2)
s.plot(kind = 'kde', secondary_y=True,ax = ax2)
plt.grid()
# 繪制直方圖
# 呈現(xiàn)較明顯的正太性

這里的直方圖呈現(xiàn)出非常明顯的正態(tài)分布特性。

QQ圖判斷

# QQ圖通過把測試樣本數(shù)據(jù)的分位數(shù)與已知分布相比較，從而來檢驗數(shù)據(jù)的分布情況

# QQ圖是一種散點圖，對應(yīng)于正態(tài)分布的QQ圖，就是由標(biāo)準(zhǔn)正態(tài)分布的分位數(shù)為橫坐標(biāo)，樣本值為縱坐標(biāo)的散點圖
# 參考直線：四分之一分位點和四分之三分位點這兩點確定，看散點是否落在這條線的附近

# 繪制思路
# ① 在做好數(shù)據(jù)清洗后，對數(shù)據(jù)進行排序（次序統(tǒng)計量：x(1)&lt;x(2)&lt;....&lt;x(n)）
# ② 排序后，計算出每個數(shù)據(jù)對應(yīng)的百分位p{i}，即第i個數(shù)據(jù)x(i)為p(i)分位數(shù)，其中p(i)=(i-0.5)/n （pi有多重算法，這里以最常用方法為主）
# ③ 繪制直方圖 + qq圖，直方圖作為參考

s = pd.DataFrame(np.random.randn(1000)+10,columns = ['value'])
print(s.head())
# 創(chuàng)建隨機數(shù)據(jù)

mean = s['value'].mean()
std = s['value'].std()
print('均值為：%.2f，標(biāo)準(zhǔn)差為：%.2f' % (mean,std))
print('------')
#  計算均值，標(biāo)準(zhǔn)差

s.sort_values(by = 'value', inplace = True)  # 重新排序
print(s.head())
s_r = s.reset_index(drop = False)  # 重新排序后，更新index
print("----------\n", s_r.head())
s_r['p'] = (s_r.index - 0.5) / len(s_r)  
s_r['q'] = (s_r['value'] - mean) / std
print(s_r.head())
print('------')
# 計算百分位數(shù) p(i)
# 計算q值

# st = s['value'].describe()
# x1 ,y1 = 0.25, st['25%']
# x2 ,y2 = 0.75, st['75%']
# print('四分之一位數(shù)為：%.2f，四分之三位數(shù)為：%.2f' % (y1,y2))
# print('------')
# # 計算四分之一位數(shù)、四分之三位數(shù)

# fig = plt.figure(figsize = (10,9))
# ax1 = fig.add_subplot(3,1,1)  # 創(chuàng)建子圖1
# ax1.scatter(s.index, s.values)
# plt.grid()
# # 繪制數(shù)據(jù)分布圖

# ax2 = fig.add_subplot(3,1,2)  # 創(chuàng)建子圖2
# s.hist(bins=30,alpha = 0.5,ax = ax2)
# s.plot(kind = 'kde', secondary_y=True,ax = ax2)
# plt.grid()
# # 繪制直方圖

# ax3 = fig.add_subplot(3,1,3)  # 創(chuàng)建子圖3
# ax3.plot(s_r['p'],s_r['value'],'k.',alpha = 0.1)
# ax3.plot([x1,x2],[y1,y2],'-r')
# plt.grid()
# # 繪制QQ圖，直線為四分之一位數(shù)、四分之三位數(shù)的連線，基本符合正態(tài)分布

KS檢驗，理論推導(dǎo)

使用K-S檢驗一個數(shù)列是否服從正態(tài)分布、兩個數(shù)列是否服從相同的分布

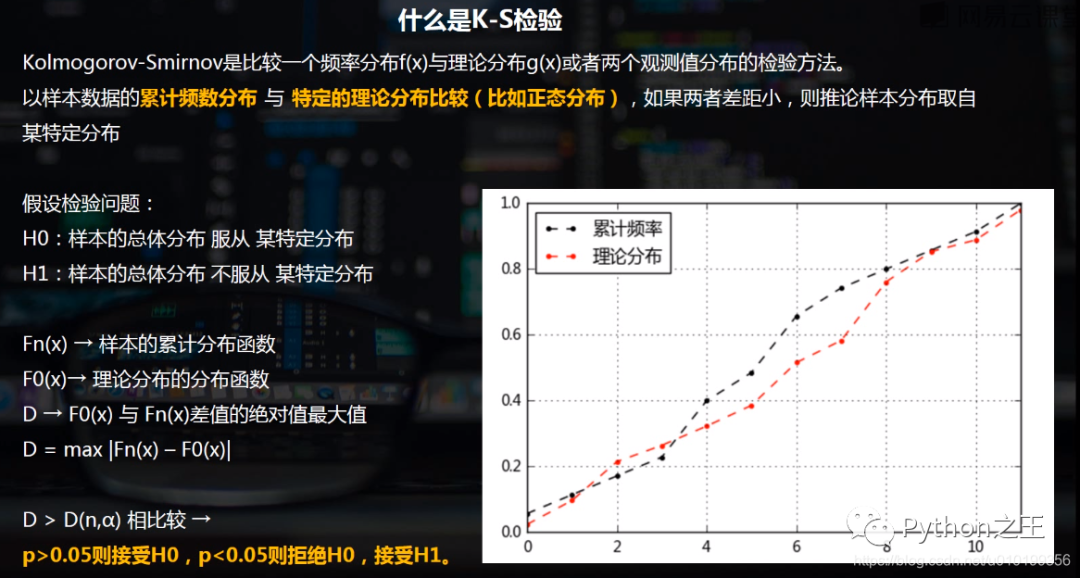
使用K-S檢驗一個數(shù)列是否服從正態(tài)分布、兩個數(shù)列是否服從相同的分布 data = [87,77,92,68,80,78,84,77,81,80,80,77,92,86, 76,80,81,75,77,72,81,72,84,86,80,68,77,87, 76,77,78,92,75,80,78] # 樣本數(shù)據(jù)，35位健康男性在未進食之前的血糖濃度

df = pd.DataFrame(data, columns =['value'])
u = df['value'].mean()
std = df['value'].std()
print("樣本均值為：%.2f，樣本標(biāo)準(zhǔn)差為：%.2f" % (u,std))
print('------')
# 查看數(shù)據(jù)基本統(tǒng)計量

s = df['value'].value_counts().sort_index()
df_s = pd.DataFrame({'血糖濃度':s.index,'次數(shù)':s.values})
# 創(chuàng)建頻率數(shù)據(jù)

df_s['累計次數(shù)'] = df_s['次數(shù)'].cumsum()
df_s['累計頻率'] = df_s['累計次數(shù)'] / len(data)

# len(data)

df_s['標(biāo)準(zhǔn)化取值'] = (df_s['血糖濃度'] - u) / std
df_s['理論分布'] =[0.0244,0.0968,0.2148,0.2643,0.3228,0.3859,0.5160,0.5832,0.7611,0.8531,0.8888,0.9803]  # 通過查閱正太分布表
df_s['D'] = np.abs(df_s['累計頻率'] - df_s['理論分布'])
dmax = df_s['D'].max()
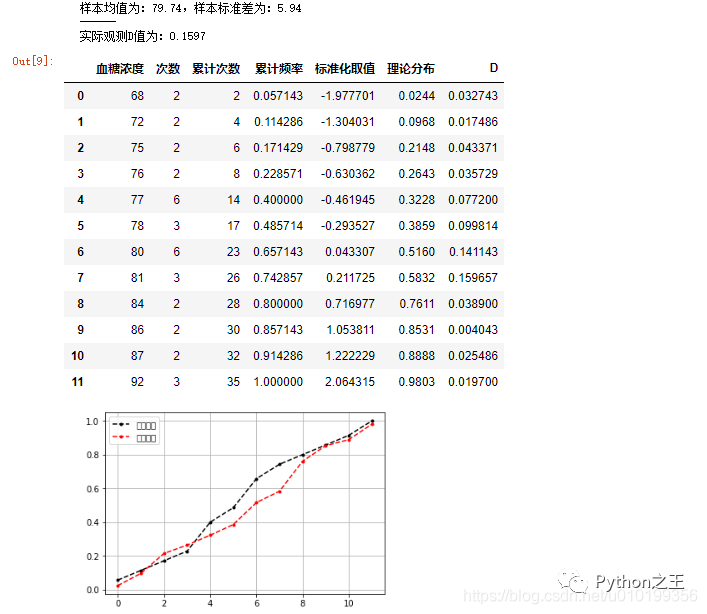
print("實際觀測D值為：%.4f" % dmax)
# D值序列計算結(jié)果表格

df_s['累計頻率'].plot(style = '--k.')
df_s['理論分布'].plot(style = '--r.')
plt.legend(loc = 'upper left')
plt.grid()
# 密度圖表示

df_s

下面是正態(tài)分布表和顯著性對照表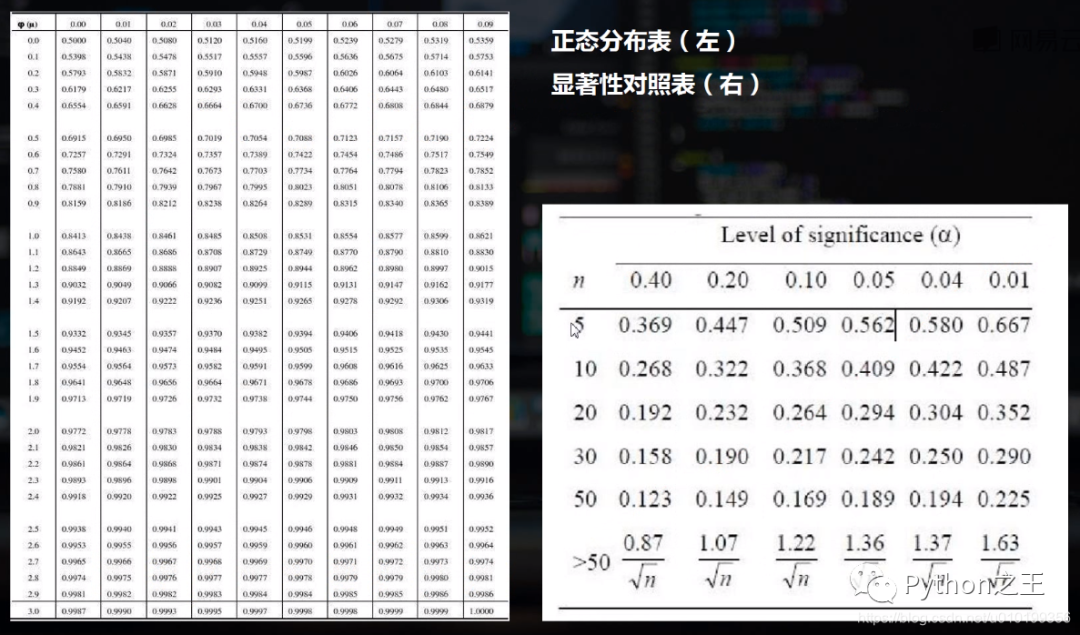因為樣本數(shù)為35，大于30且小于50，所以p值在這個區(qū)間另外的，由于D值為0.1597. 大于0.158，小于0.197，且樣本數(shù)量接近于30.所以我們可以認(rèn)為P值的取值區(qū)間在0.20 - 0.40 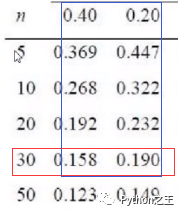滿足p > 0.5的情況，所以服從正態(tài)分布。

直接用算法做KS檢驗

from scipy import stats
# scipy包是一個高級的科學(xué)計算庫，它和Numpy聯(lián)系很密切，Scipy一般都是操控Numpy數(shù)組來進行科學(xué)計算

data = [87,77,92,68,80,78,84,77,81,80,80,77,92,86,
       76,80,81,75,77,72,81,72,84,86,80,68,77,87,
       76,77,78,92,75,80,78]
# 樣本數(shù)據(jù)，35位健康男性在未進食之前的血糖濃度

df = pd.DataFrame(data, columns =['value'])
u = df['value'].mean()  # 計算均值
std = df['value'].std()  # 計算標(biāo)準(zhǔn)差
stats.kstest(df['value'], 'norm', (u, std))
# .kstest方法：KS檢驗，參數(shù)分別是：待檢驗的數(shù)據(jù)，檢驗方法（這里設(shè)置成norm正態(tài)分布），均值與標(biāo)準(zhǔn)差
# 結(jié)果返回兩個值：statistic → D值，pvalue → P值
# p值大于0.05，為正態(tài)分布