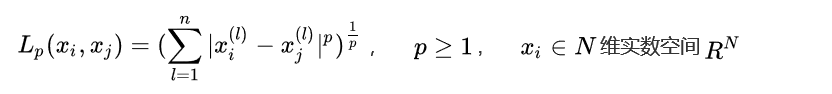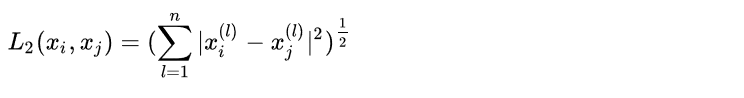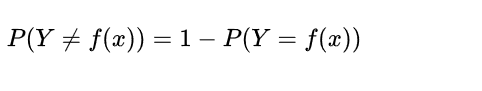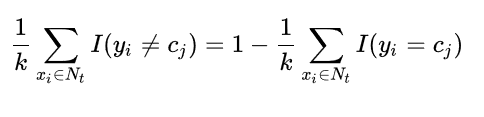如何優(yōu)雅地實現(xiàn)KNN搜索
我們知道K近鄰法(K-Nearest Neighbor, KNN)是一種基本的機器學(xué)習(xí)算法,早在1968年就被提出。KNN算法簡單、直觀,是最著名的“惰性學(xué)習(xí)”算法,不具有顯示的學(xué)習(xí)過程。
正因為其算法的思想簡單,我們更加關(guān)注KNN算法實現(xiàn)的優(yōu)化。最簡單粗暴的就是線性掃描,但隨著樣本量的放大,其計算量也會成倍放大,因此本文介紹并實現(xiàn)一種優(yōu)雅的優(yōu)化搜索方法——KD樹。
K近鄰?fù)茖?dǎo)與KD樹過程
我們可以用文字簡單描述下KNN算法:給定一個訓(xùn)練數(shù)據(jù)集T,對于新的目標(biāo)實例x,我們在訓(xùn)練集T中找到與實例x最鄰近的k個實例,這k個實例大多屬于哪一類,目標(biāo)實例x就被分為這個類。
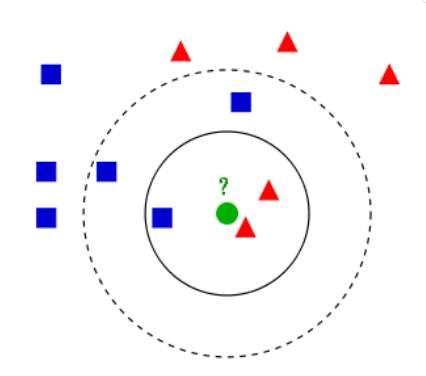
用數(shù)學(xué)公式我們表達(dá)如下:
給定訓(xùn)練數(shù)據(jù)集T:
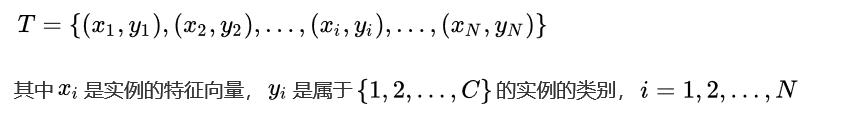
根據(jù)給定的新的目標(biāo)實例Xtarget,和距離度量方法,我們可以在T中找到k個與Xtarget最鄰近的實例點,我們將這k個近鄰點的集合記作Nk:
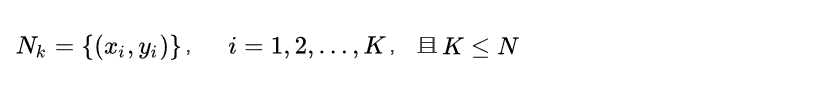
那目標(biāo)實例的類別Ytarget為:
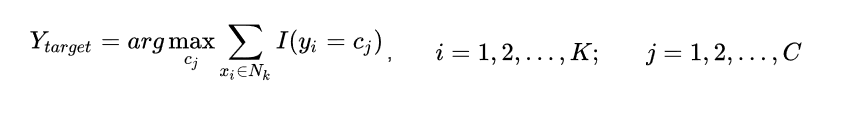
此處的I為指數(shù)函數(shù),當(dāng)yi=cj時為1,否則為0。
KD樹的實現(xiàn)
構(gòu)造KD樹
通常,依次選擇坐標(biāo)軸對空間切分,選擇訓(xùn)練實例點在選定坐標(biāo)軸上的中位數(shù)(median)為切分點,這樣得到的KD樹是平衡的,但是平衡的KD樹搜索時的效率未必是最優(yōu)的。
切分超平面左側(cè)區(qū)域?qū)?yīng)的是小于選定坐標(biāo)軸的實例點,右側(cè)區(qū)域?qū)?yīng)的是大于選定坐標(biāo)軸的實例點,將落在切分超平面上的實例點保存在根結(jié)點。
當(dāng)左右兩個子區(qū)域沒有實例存在時停止劃分,從而形成KD樹的區(qū)域劃分。
舉個例子:給定二維數(shù)據(jù)集T={(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)},進(jìn)行區(qū)域劃分。

搜索KD樹
利用KD樹可以省去對大部分?jǐn)?shù)據(jù)點的搜索,從而減少搜索的計算量,以最近鄰為例:給定一個目標(biāo)點,搜索其最近鄰,首先找到包含目標(biāo)點的葉結(jié)點;然后從該葉結(jié)點出發(fā),依次回退到父結(jié)點;不斷查找與目標(biāo)點最鄰近的節(jié)點,當(dāng)確定不可能存在更近的結(jié)點時終止。
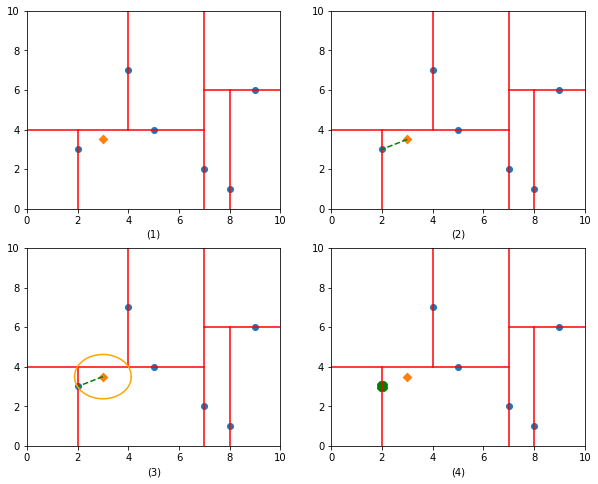
以目標(biāo)點(3, 3.5)為例,在上面構(gòu)造樹的基礎(chǔ)上進(jìn)行搜索。
首先,將目標(biāo)點劃分到(2, 3)所在的結(jié)點,初步認(rèn)定(2, 3)就是目標(biāo)點的最近鄰;
其次,計算(2, 3)與(3, 3.5)之間的距離d;
然后,往父結(jié)點回溯,以(3, 3.5)為中心,距離d為半徑畫圓,發(fā)現(xiàn)圓圈與其父結(jié)點相交;
最后,計算目標(biāo)點與父結(jié)點上的(5, 4)以及另一側(cè)上的(4, 7)距離,發(fā)現(xiàn)其最近鄰的點還是(2, 3);
再往上一層父結(jié)點遞歸,發(fā)現(xiàn)切分超平面并不與圓圈相交,故結(jié)束搜索。
以上是K近鄰與KD樹的推導(dǎo)部分。
Python實現(xiàn)K近鄰與KD樹
提前說明下,這里寫的KD樹實現(xiàn)K近鄰算法,其最終結(jié)果并不是輸出Y值,而是輸出與目標(biāo)樣例近鄰的前K個訓(xùn)練數(shù)據(jù)中的樣例,這樣可以清楚地看到KD樹的運行軌跡。得到了K近鄰,要輸出最終的結(jié)果也是易如反掌,自己加一段投票策略即可。
首先,先建立了樹的類,用來存儲一些重要信息。
# KdTree
Python
import numpy as np
import matplotlib.pyplot as plt
#樹結(jié)構(gòu)類
class Tree(object):
def __init__(self, cutColumn=None, cutValue=None):
Parameters
----------
cutColumn : Int, optional
切分超平面的特征列. The default is None.
cutValue : float, optional
切分超平面的特征值. The default is None.
self.cutColumn = cutColumn
self.cutValue = cutValue
self.nums = 0 #個數(shù)
self.rootNums = 0 #在切分超平面上面的實例個數(shù)
self.leftNums = 0 #在切分超平面左側(cè)的實例個數(shù)
self.rightNums = 0 #在切分超平面右側(cè)的實例個數(shù)
self._tree_left = None #左側(cè)樹結(jié)構(gòu)
self._tree_right = None #右側(cè)樹結(jié)構(gòu)
self.depth = 0 #樹的深度
其次,正式構(gòu)造一個KNN類,初始化一些屬性。
#KD樹實現(xiàn)KNN算法
class KNN(object):
def __init__(self, K=1):
self.K_neighbor = K
self.tree_depth = 0
self.n_samples = 0
self.n_features = 0
self.trainSet = 0
self.label = 0
self._tree = 0
然后,寫一些用得到的方法。有計算切分的特征列、計算切分的特征值、計算歐式距離、計算數(shù)據(jù)集中距離目標(biāo)樣本點的前K個近鄰。
def cal_cutColumn(self, n_iter):
return np.mod(n_iter, self.n_features)
def cal_cutValue(self, Xarray):
if Xarray.__len__() % 2 == 1:
#單數(shù)序列
cutValue = np.median(Xarray)
else:
#雙數(shù)序列
cutValue = Xarray[np.argsort(Xarray)[int(Xarray.__len__()/2)]]
return cutValue
#計算歐氏距離
def caldist(self, X, xi):
return np.linalg.norm((X-xi), axis=1)
#計算一堆數(shù)據(jù)集距離目標(biāo)點的距離,并返回K個最近值
def calKneighbor(self, XIndex, xi):
trainSet = self.trainSet[XIndex,:]
knnDict = {}
distArr = self.caldist(trainSet, xi)
neighborIndex = XIndex[np.argsort(distArr)[:self.K_neighbor]]
neighborDist = distArr[np.argsort(distArr)[:self.K_neighbor]]
for i, j in zip(neighborIndex, neighborDist):
knnDict[i] = j
return knnDict
<<<< 滑動查看完整代碼 >>>>接著,是構(gòu)造KD樹的代碼部分。主體部分是fit_tree(),其中的build_tree()部分遞歸生成樹的結(jié)構(gòu)。
#造樹
def build_tree(self, X, n_iter=0):
nums = X.shape[0]
#不達(dá)切分條件,則不生成樹,直接返回None
if nums < 2*self.K_neighbor:
return None
#計算切分的列
cutColumn = self.cal_cutColumn(n_iter)
Xarray = X[:,cutColumn]
#計算切分的值
cutValue = self.cal_cutValue(Xarray)
#生成當(dāng)前的樹結(jié)構(gòu)
tree = Tree(cutColumn, cutValue)
rootIndex = np.nonzero(Xarray==cutValue)[0]
leftIndex = np.nonzero(Xarray<cutValue)[0]
rightIndex = np.nonzero(Xarray>cutValue)[0]
#保存樹的結(jié)點數(shù)量
tree.nums = nums
tree.rootNums = len(rootIndex)
tree.leftNums = len(leftIndex)
tree.rightNums = len(rightIndex)
#保存樹深,并加1
tree.depth = n_iter
n_iter += 1
#遞歸添加左側(cè)樹枝結(jié)構(gòu)
X_left = X[leftIndex,:]
tree._tree_left = self.build_tree(X_left, n_iter)
#遞歸添加右側(cè)樹枝結(jié)構(gòu)
X_right = X[rightIndex,:]
tree._tree_right = self.build_tree(X_right, n_iter)
return tree
#訓(xùn)練構(gòu)造KD樹
def fit_tree(self, X, y):
self.n_samples, self.n_features = X.shape
self.trainSet = X
self.label = y
self._tree = self.build_tree(X)
return<<<< 滑動查看完整代碼 >>>>
最后,是搜索KD樹的代碼部分。transform_tree()是主體部分,search_tree()對樹進(jìn)行遞歸搜索以及結(jié)點的回退搜索。
#遞歸搜索樹
def search_tree(self, trainSetIndex, tree, xi):
trainSet = self.trainSet[trainSetIndex,:]
#搜索樹找到子結(jié)點的過程
if not (tree._tree_left or tree._tree_right):
self.neighbor = self.calKneighbor(trainSetIndex, xi)
print("樹深度為{},切分平面為第{}列特征,初始化搜索樹結(jié)束!找到{}個近鄰點".format(tree.depth, tree.cutColumn, self.K_neighbor))
return
else:
cutColumn = tree.cutColumn
cutValue = tree.cutValue
#切分平面左邊的實例
chidlLeftIndex = trainSetIndex[np.nonzero(trainSet[:,cutColumn]<cutValue)[0]]
#切分平面上的實例
rootIndex = trainSetIndex[np.nonzero(trainSet[:,cutColumn]==cutValue)[0]]
#切分平面右邊的實例
chidlRightIndex = trainSetIndex[np.nonzero(trainSet[:,cutColumn]>cutValue)[0]]
if xi[cutColumn] <= cutValue:
self.search_tree(chidlLeftIndex, tree._tree_left, xi)
#回退父結(jié)點的過程
#判斷目標(biāo)點到該切分平面的的距離,計算是否相交
length = abs(tree.cutValue - xi[cutColumn])
#不相交的話,則繼續(xù)回退
if length >= max(self.neighbor.values()):
print("樹深度為%d,切分平面為第%d列特征,和父結(jié)點的切分平面不相交!"%(tree.depth, tree.cutColumn))
return
#相交的話,先是計算分類平面上實例點的距離,再計算另外半邊的實例點的距離
else:
targetIndex = list(rootIndex) + list(chidlRightIndex) + list(self.neighbor.keys())
self.neighbor = self.calKneighbor(np.array(targetIndex), xi)
print("樹深度為%d,切分平面為第%d列特征,檢測父結(jié)點切分平面和另一側(cè)的樣本點是否有更小的!"%(tree.depth, tree.cutColumn))
return
else:
self.search_tree(chidlRightIndex, tree._tree_right, xi)
#回退父結(jié)點進(jìn)行判斷
length = abs(tree.cutValue - xi[cutColumn])
if length >= max(self.neighbor.values()):
print("樹深度為%d,切分平面為第%d列特征,和父結(jié)點的切分平面不相交!"%(tree.depth, tree.cutColumn))
return
else:
targetIndex = list(rootIndex) + list(chidlLeftIndex) + list(self.neighbor.keys())
self.neighbor = self.calKneighbor(np.array(targetIndex), xi)
print("樹深度為%d,切分平面為第%d列特征,檢測父結(jié)點切分平面和另一側(cè)的樣本點是否有更小的!"%(tree.depth, tree.cutColumn))
return
#搜索KD樹
def transform_tree(self, Xi):
self.neighbor = dict()
self.search_tree(np.arange(self.n_samples), self._tree, Xi)
return self.neighbor
<<<< 滑動查看完整代碼 >>>>
代碼寫完,我們用鳶尾花數(shù)據(jù)集來測試下,KD樹找到的k個最近鄰的樣本是否準(zhǔn)確。
首先,我們先導(dǎo)入鳶尾花數(shù)據(jù)集,隨意寫一個目標(biāo)樣本點,并線性地算出從小到大距離這個目標(biāo)樣本點的所有樣本的順序。我們print出來可以看到下標(biāo)為35的鳶尾花原數(shù)據(jù)集是距離目標(biāo)樣本最近的點,然后依次是1, 45, 34, 12, 49, 2......
#鳶尾花數(shù)據(jù)集測試
from sklearn.datasets import load_iris
X, y = load_iris(True)
#線性計算目標(biāo)集的最小距離下標(biāo)
targetX = np.array([5, 3, 1.2, 0.3])
minDistIndex = np.argsort(np.linalg.norm((X-targetX), axis=1))
<<<< 滑動查看完整代碼 >>>>

然后,我們通過自己寫的KD樹,分別取K=1, 2, 3, 5, 10來驗證下是否正確。
#K=1時
knn = KNN(K=1)
knn.fit_tree(X, y)
knn.transform_tree(targetX)
#K=2時
knn = KNN(K=2)
knn.fit_tree(X, y)
knn.transform_tree(targetX)
#K=3時
knn = KNN(K=3)
knn.fit_tree(X, y)
knn.transform_tree(targetX)
#K=5時
knn = KNN(K=5)
knn.fit_tree(X, y)
knn.transform_tree(targetX)
#K=10時
knn = KNN(K=10)
knn.fit_tree(X, y)
knn.transform_tree(targetX)
K=1時,

K=2時,
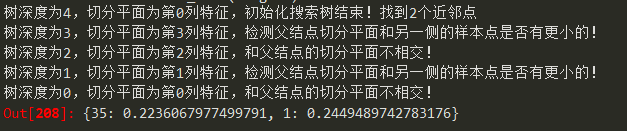
K=3時,

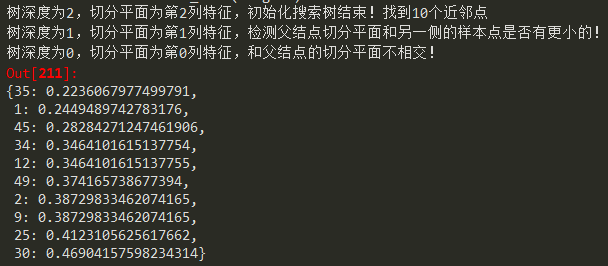
K=5時,

K=10時,
作者:TalkingData金融咨詢團(tuán)隊 張偉
轉(zhuǎn)載請聯(lián)系獲取授權(quán)
推薦閱讀:

TalkingData——用數(shù)據(jù)說話
每天一篇好文章,歡迎分享關(guān)注