一文通俗講透決策樹模型
決策樹模型因為其特征預(yù)處理簡單、易于集成學(xué)習(xí)、良好的擬合能力及解釋性，是應(yīng)用最廣泛的機器學(xué)習(xí)模型之一。
不同于線性模型【數(shù)學(xué)描述：f(W*X +b)】是通過數(shù)據(jù)樣本學(xué)習(xí)各個特征的合適權(quán)重，加權(quán)后做出決策。決策樹會選擇合適特征并先做特征劃分后，再做出決策（也就是決策邊界是非線性的，這提高了模型的非線性能力）。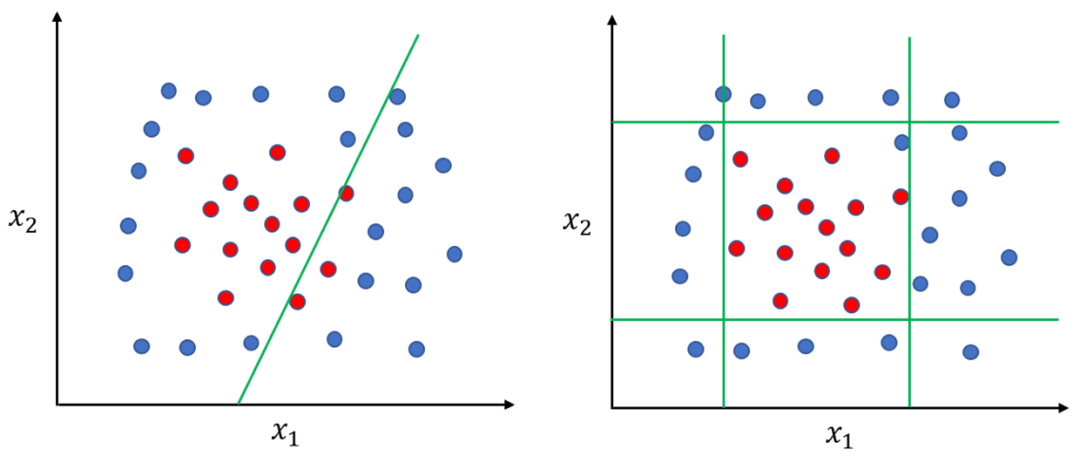
一、樹模型的概括
決策樹呈樹形結(jié)構(gòu)，更通俗來講，樹模型的數(shù)學(xué)描述就是“分段函數(shù)”。如下一個簡單判別西瓜質(zhì)量的決策樹模型示例（注：以下西瓜示例，數(shù)據(jù)隨機杜撰的，請忽略這么小的西瓜瓜~）：
學(xué)習(xí)這樣樹模型的過程，簡單來說就是從有監(jiān)督的數(shù)據(jù)經(jīng)驗中學(xué)習(xí)一個較優(yōu)的樹模型的結(jié)構(gòu)：包含了依次地選擇特征、確定特征閾值做劃分的內(nèi)部節(jié)點及最終輸出葉子節(jié)點的數(shù)值或類別結(jié)果。
1、我們首先要拿到一些有關(guān)西瓜的有監(jiān)督數(shù)據(jù)（這些西瓜樣本已有標(biāo)注高/低質(zhì)量西瓜），并嘗試選用決策樹模型來學(xué)習(xí)這個劃分西瓜的任務(wù)。如下數(shù)據(jù)樣本示例：
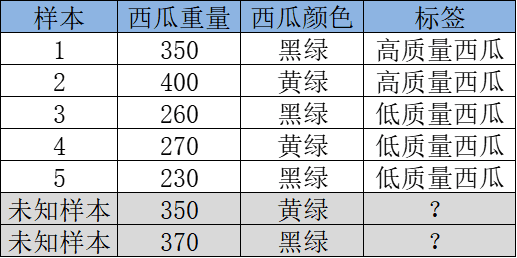
2、后面也就是，憑著已知西瓜樣本的特性/特征【如：西瓜重量、西瓜顏色】，學(xué)習(xí)如何正確地劃分這些西瓜（歸納出本質(zhì)規(guī)律）。開始學(xué)習(xí)之前，我們得確定一個樹模型在生長的目標(biāo)（學(xué)習(xí)的目標(biāo)）。簡單來說，也就是在當(dāng)前節(jié)點以什么為目標(biāo)來指導(dǎo)怎么選擇特征及分裂，而劃分得好也就是要劃分出的各組的準(zhǔn)確率（純度）都比較高。
3、然后，根據(jù)學(xué)習(xí)目標(biāo)，簡單的我們可以通過遍歷計算所有特征不同閾值的劃分效果。選擇各個的特征及嘗試特征的所有實際取值，看以哪個特征閾值劃分西瓜質(zhì)量的效果較好。這個過程也就是確定選擇特征及特征閾值劃分的優(yōu)化算法。
4、最終的，按照上面的步驟，我們逐個特征及取值試著去劃分后發(fā)現(xiàn)，根據(jù)西瓜重量的特征 以300g作為劃分出了兩組，我們以葉子節(jié)點的大多數(shù)類作為該節(jié)點的決策類別。可能發(fā)現(xiàn)<300的組 里面低質(zhì)量西瓜占比100%，>300 那組 高質(zhì)量西瓜占比99%，整體分類效果是不錯的，最終就確定下了這樣的一個決策樹模型。
二、樹模型的要素
從上述例子，我們可以將樹模型的學(xué)習(xí)可以歸到經(jīng)典機器學(xué)習(xí)的4個要素：
2.0 已知(標(biāo)簽)的數(shù)據(jù) 2.1 樹模型的結(jié)構(gòu)（分段函數(shù)結(jié)構(gòu)：特征劃分+決策結(jié)果） 2.2 學(xué)習(xí)目標(biāo) 2.3 優(yōu)化算法
樹模型通過結(jié)合這幾個要素，更快更好地劃分特征空間，得出比較準(zhǔn)確的決策。如下對這幾個要素具體解析。
2.1 樹模型的結(jié)構(gòu)
樹模型的結(jié)構(gòu)也就是個分段函數(shù)，包含了 選定特征做閾值劃分（內(nèi)部節(jié)點），以及劃分后賦值的分?jǐn)?shù)或類別決策（葉子節(jié)點）。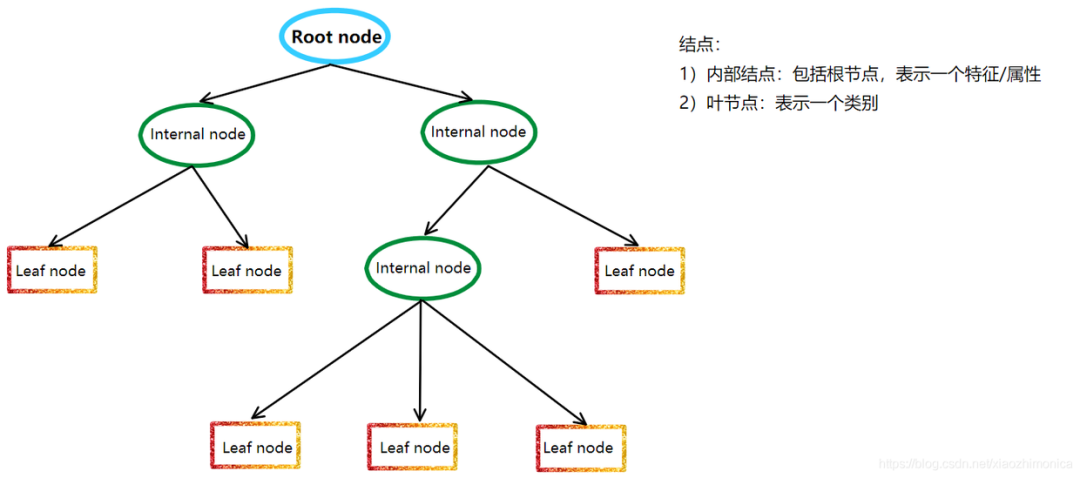
2.1.1學(xué)習(xí)樹結(jié)構(gòu)的過程
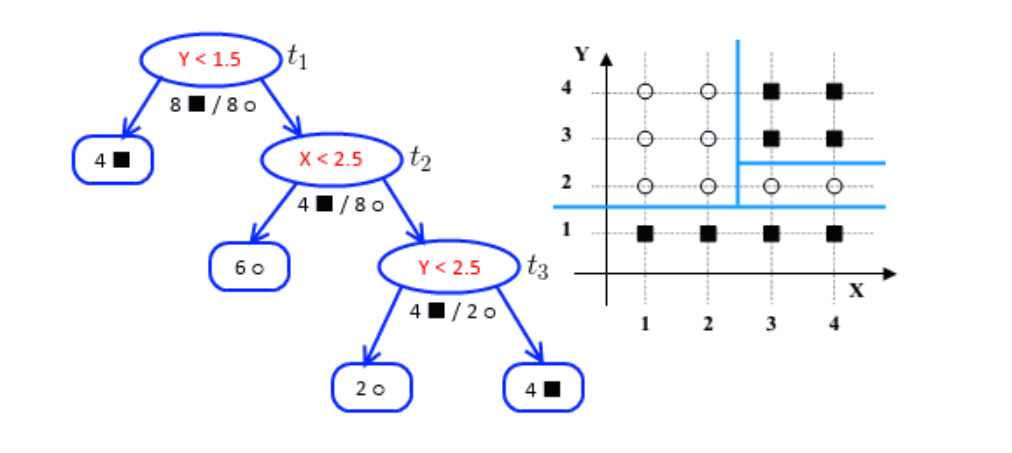
學(xué)習(xí)樹模型的關(guān)鍵在于依據(jù)某些學(xué)習(xí)目標(biāo)/指標(biāo)（如劃分準(zhǔn)確度、信息熵、Gini不純度、均方誤差的增益量）去選擇當(dāng)前最優(yōu)的特征并對樣本的特征空間做非線性準(zhǔn)確的劃分，如上面西瓜的例子選擇了一個特征做了一次劃分（一刀切），通常情況下僅僅一刀切的劃分準(zhǔn)確度是不夠的，可能還要在前面劃分的樣本基礎(chǔ)上，繼續(xù)多劃分幾次（也就多個切分條件的分段函數(shù)，如 if a>300 且特征b>10 且特征c<100， then 決策結(jié)果1；），以達(dá)到更高的準(zhǔn)確度（純度）。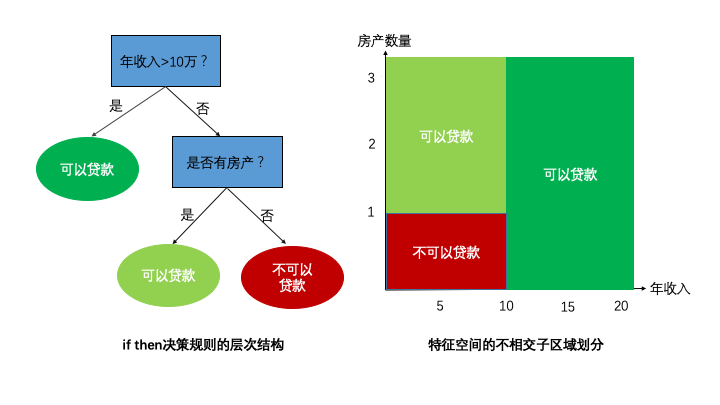
但是，隨著切分次數(shù)的變多，樹的復(fù)雜度提高也就容易過擬合，相應(yīng)每個切分出的小子特征空間的統(tǒng)計信息可能只是噪音。減少樹生長過程的過擬合的風(fēng)險，一個重要的方法就是樹的剪枝，剪枝是一種正則化：由于決策樹容易對數(shù)據(jù)產(chǎn)生過擬合，即生長出結(jié)構(gòu)過于復(fù)雜的樹模型，這時局部的特征空間會越分越“小”得到了不靠譜的“統(tǒng)計噪聲”。通過剪枝算法可以降低復(fù)雜度，減少過擬合的風(fēng)險。
決策樹剪枝的目的是極小化經(jīng)驗損失+結(jié)構(gòu)損失，基本策略有”預(yù)剪枝“和”后剪枝“兩種策略：①預(yù)剪枝：是在決策樹生成過程中，限制劃分的最大深度、葉子節(jié)點數(shù)和最小樣本數(shù)目等，以減少不必要的模型復(fù)雜度；②后剪枝：是先從訓(xùn)練集生成一棵完整的決策樹，然后用用驗證集自底向上地對非葉結(jié)點進(jìn)行考察，若將該節(jié)點對應(yīng)的子樹替換為葉子結(jié)點（剪枝）能帶來決策樹的泛化性能提升（即目標(biāo)函數(shù)損失更小，常用目標(biāo)函數(shù)如：loss = 模型經(jīng)驗損失bias+ 模型結(jié)構(gòu)損失α|T|， T為節(jié)點數(shù)目, α為系數(shù)），則將該子樹替換為葉子結(jié)點。
2.1.2 復(fù)雜樹結(jié)構(gòu)的進(jìn)階
樹模型的集成學(xué)習(xí)
實踐中可以發(fā)現(xiàn)，淺層的樹很容易欠擬合，而通過加深樹的深度，雖然可以提高訓(xùn)練集的準(zhǔn)確度，卻很容易過擬合。
這個角度來看，單個樹模型是比較弱的，且很容易根據(jù)特征選擇、深度等超參數(shù)調(diào)節(jié)各樹模型的多樣性。正因為這些特點，決策樹很適合通過結(jié)合多個的樹模型做集成學(xué)習(xí)進(jìn)一步提升模型效果。
集成學(xué)習(xí)是結(jié)合一些的基學(xué)習(xí)器共同學(xué)習(xí)，來改進(jìn)其泛化能力和魯棒性的方法，主流的有兩種集成思想：
并行方式（bagging）：獨立的訓(xùn)練一些基學(xué)習(xí)器，然后（加權(quán)）平均它們的預(yù)測結(jié)果。代表模型如：Random Forests；
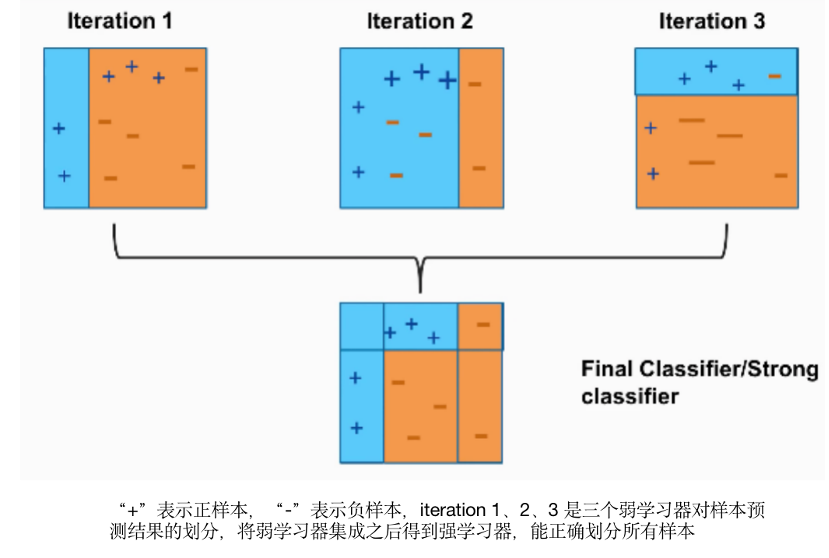
串行方式（boosting）：一個接一個的(串行)訓(xùn)練基學(xué)習(xí)器，每一個基學(xué)習(xí)器主要用來修正前面學(xué)習(xí)器的偏差。代表模型如：AdaBoost、GBDT及XGBOOST；（擴展：像基于cart回歸樹的GBDT集成方法，通過引入了損失函數(shù)的梯度去代替殘差，這個過程也類似局部的梯度下降算法）
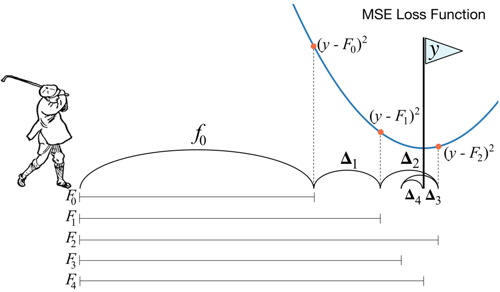
線性決策樹
樹模型天然具有非線性的特點，但與此有個缺陷，樹模型卻學(xué)習(xí)不好簡單的線性回歸！可以簡單構(gòu)想下傳統(tǒng)決策樹表達(dá) y=|2x|這樣規(guī)律，需要怎么做？如 if x=1,then 2; x =3， then 6 .....；這樣窮舉顯然不可能的。這里介紹下線性決策樹，其實原理也很簡單：把線性回歸加到?jīng)Q策樹的葉子節(jié)點里面（特征劃分完后，再用線性模型擬合做決策）。一個簡單線性樹模型用分段函數(shù)來表示如：if x >0, then 2x;代表模型有 linear decision tree， GBDT-PL等模型。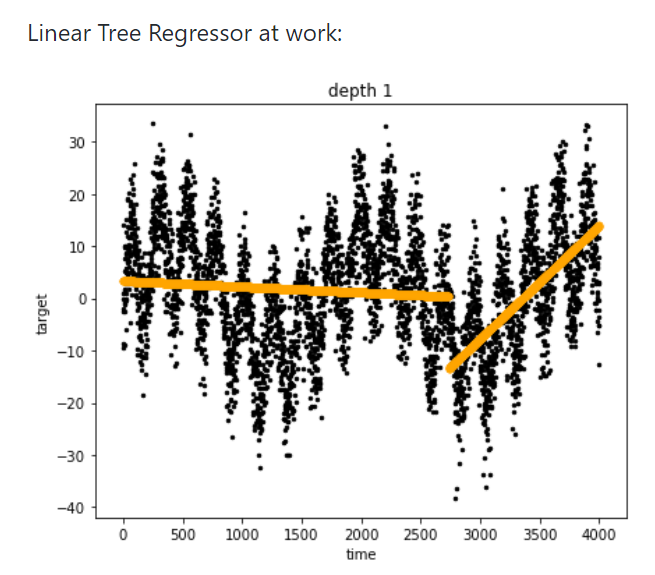
2.2 學(xué)習(xí)目標(biāo)（目標(biāo)函數(shù)）
上文有提到，樹模型的學(xué)習(xí)目標(biāo)就是讓各組的劃分的準(zhǔn)確率（純度）都比較高，減小劃分誤差損失（此處忽略了結(jié)構(gòu)損失T）。能達(dá)成劃分前后損失差異效果類似的指標(biāo)有很多：信息熵、基尼系數(shù)、MSE損失函數(shù)等等 都可以評估劃分前后的純度的增益 ，其實都是對分類誤差的一種衡量，不同指標(biāo)也對應(yīng)這不同類型的決策樹方法。
ID3決策樹的指標(biāo):信息增益（information gain） 信息增益定義為集合 D 的經(jīng)驗熵 H(D) 與特征 A 給定條件下 D 的經(jīng)驗條件熵 H(D|A) 之差，也就是信息熵減去條件信息熵，表示得知特征X的信息而使得Y的信息的不確定性減少的程度（信息增益越大，表示已知X的情況下， Y基本就確定了）。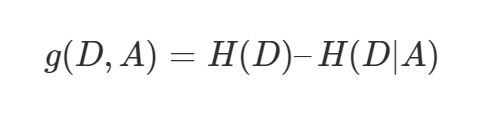 
使用信息增益做特征劃分的缺點是：信息增益偏向取值較多的特征。當(dāng)特征的取值較多時，根據(jù)此特征劃分更容易得到純度更高的子集，因此劃分之后的熵更低，由于劃分前的熵是一定的，因此信息增益更大，因此信息增益比較偏向取值較多的特征。
C4.5決策樹的指標(biāo)：信息增益比
信息增益比也就是信息增益除以信息熵，這樣可以減少偏向取值較多信息熵較大的特征。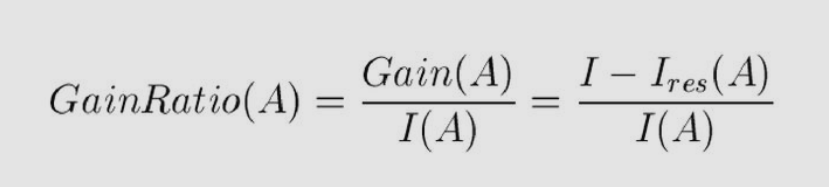
相應(yīng)的，使用信息增益比缺點是：信息增益比偏向取值較少的特征。綜上兩種指標(biāo)，可以在候選特征中找出信息增益高于平均水平的特征，然后在這些特征中再選擇信息增益率最高的特征。
Cart決策樹的指標(biāo)：基尼系數(shù)（分類樹） 或 平方誤差損失（回歸）
與信息熵一樣（信息熵 如下式）
基尼系數(shù)表征的也是事件的不確定性（不純度），也都可以看做是對分類誤差率的衡量。
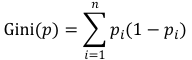
我們將熵定義式中的“-log(pi)”替換為 1-pi 也就是基尼系數(shù)，因為-log(pi)的泰勒近似展開第一項就是1-pi。基尼系數(shù)簡單來看就是熵的“平替版”，在衡量分類誤差的同時，也簡化了大量計算。
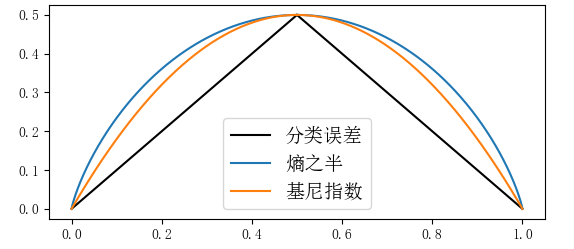
（注：由于分類誤差為分段函數(shù)=1-max(p, 1-p) ，不便于微分計算，實際中也比較少直接用）
當(dāng)Cart應(yīng)用于回歸任務(wù)，平方誤差損失也就是Cart回歸樹的生長指標(biāo)。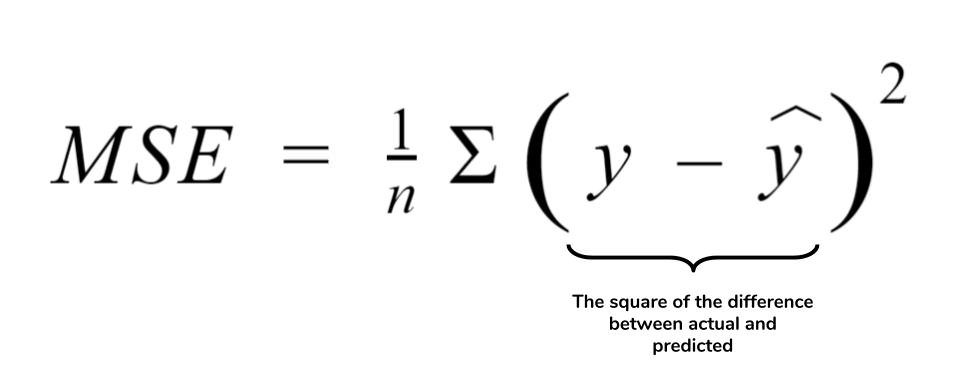
2.3 優(yōu)化算法
確認(rèn)學(xué)習(xí)目標(biāo)，而依據(jù)這個指標(biāo)去學(xué)習(xí)具體樹結(jié)構(gòu)的方法（優(yōu)化算法），基本上有幾種思路：
暴力枚舉：嘗試所有可能的特征劃分及組合，以找到目標(biāo)函數(shù)最優(yōu)的樹結(jié)構(gòu)。但在現(xiàn)實任務(wù)中這基本是不可能的。
自上而下的貪心算法：每一步（節(jié)點）都選擇現(xiàn)在最優(yōu)（信息增益、gini、平方誤差損失）的特征劃分，最終生成一顆決策樹，這也是決策樹普遍的啟發(fā)式方法，代表有：cart樹、ID3、C4.5樹等等
隨機優(yōu)化：隨機選擇特征及劃分方式，通常這種方法單樹的生長較快且復(fù)雜度較高。模型的隨機性、偏差比較大（模型的方差相對較小，不容易過擬合，但是bias較大），所以常用集成bagging的思路進(jìn)一步優(yōu)化收斂。代表有：Extremely randomized trees（極端隨機樹）、孤立森林等等.
總結(jié)
樹模型也就是基于已知數(shù)據(jù)上， 通過以學(xué)習(xí)目標(biāo)（降低各劃分節(jié)點的誤差率）為指導(dǎo)，啟發(fā)式地選擇特征去劃分特征空間，以各劃分的葉子節(jié)點做出較"優(yōu)"的決策結(jié)果。所以，樹模型有非常強的非線性能力，但是，由于是基于劃分的局部樣本做決策，過深（劃分很多次）的樹，局部樣本的統(tǒng)計信息可能失準(zhǔn)，容易過擬合。