從零開始深度學(xué)習(xí)Pytorch筆記(9)—— 計算圖與自動求導(dǎo)(下)

前文傳送門：從零開始深度學(xué)習(xí)Pytorch筆記（1）——安裝Pytorch從零開始深度學(xué)習(xí)Pytorch筆記（2）——張量的創(chuàng)建（上）從零開始深度學(xué)習(xí)Pytorch筆記（3）——張量的創(chuàng)建（下）從零開始深度學(xué)習(xí)Pytorch筆記（4）——張量的拼接與切分從零開始深度學(xué)習(xí)Pytorch筆記（5）——張量的索引與變換從零開始深度學(xué)習(xí)Pytorch筆記（6）——張量的數(shù)學(xué)運算從零開始深度學(xué)習(xí)Pytorch筆記（7）—— 使用Pytorch實現(xiàn)線性回歸從零開始深度學(xué)習(xí)Pytorch筆記（8）—— 計算圖與自動求導(dǎo)（上）

在該系列的上一篇，我們介紹了使用Pytorch的重要知識點：計算圖和自動求導(dǎo)。

本篇我們繼續(xù)學(xué)習(xí)計算圖和自動求導(dǎo)。

首先，我們在上一節(jié)的計算圖上增加復(fù)雜度，例如變成這樣的計算圖：

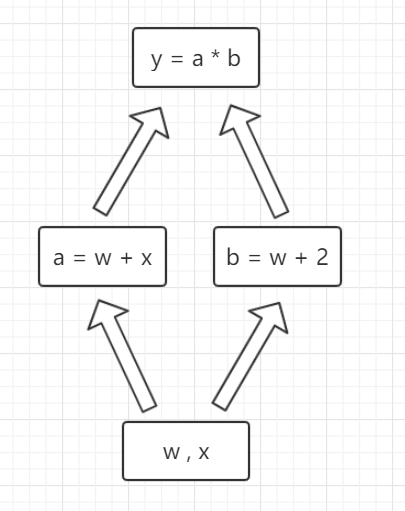
圖中為了繪制方便，把張量w和x繪制在一個框中了。

其對應(yīng)的計算圖代碼如下：

import?torch
w?=?torch.tensor([1.],requires_grad=True)
x?=?torch.tensor([2.],requires_grad=True)

a?=?torch.add(w,x)
b?=?torch.add(w,2)
y?=?torch.mul(a,b)

y.backward()#梯度反向傳播
print(w.grad)#w的梯度

需要注意的一點是，要使得某個變量支持求導(dǎo)，需要在賦值時使它的元素為浮點數(shù)值，如果例如上面代碼中的 w 和 x 張量，如果我們定義時賦值的元素不是浮點數(shù)而是整數(shù)，如下代碼：

#不用浮點數(shù)
import?torch
w?=?torch.tensor([1],requires_grad=True)
x?=?torch.tensor([2],requires_grad=True)

a?=?torch.add(w,x)
b?=?torch.add(w,2)
y?=?torch.mul(a,b)

y.backward()#梯度反向傳播
print(w.grad)#w的梯度

運行后會發(fā)現(xiàn)：

拋出的異常大概意思是：只有元素類型是浮點數(shù)的張量才能支持梯度計算。

所以這點大家要注意！

我們接著來聊聊一個新的概念，叫做葉子節(jié)點。

在pytorch的tensor類中，有個叫做 is_leaf 的屬性，可以稱之為葉子節(jié)點，如果計算圖中某個節(jié)點的 is_leaf 屬性取值為 True，則為葉子節(jié)點。如果取值是False，則不是葉子節(jié)點。

一般將用戶自己創(chuàng)建的變量叫做葉子節(jié)點，而由葉子節(jié)點計算得到的變量叫做非葉子節(jié)點，調(diào)用非葉子節(jié)點的backward方法，就會沿著非葉子節(jié)點一直回溯到葉子節(jié)點結(jié)束。

我們還是執(zhí)行一次反向傳播：

import?torch
w?=?torch.tensor([1.],requires_grad=True)
x?=?torch.tensor([2.],requires_grad=True)

a?=?torch.add(w,x)
b?=?torch.add(w,2)
y?=?torch.mul(a,b)

y.backward()#梯度反向傳播

然后查看各個節(jié)點是否葉子節(jié)點：

#查看葉子節(jié)點
print(w.is_leaf,x.is_leaf,a.is_leaf,b.is_leaf,y.is_leaf)

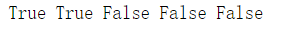
我們發(fā)現(xiàn)，其中只有我們賦值的 w 和 x 是葉子節(jié)點，而 a、b、y 是由 w 和 x 計算得到的。

我們查看一次 backward 后，每個節(jié)點的梯度值：

#查看梯度
print(w.grad,x.grad,a.grad,b.grad,y.grad)#只有葉子結(jié)點梯度存在于內(nèi)存中

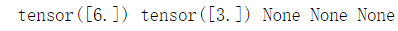
發(fā)現(xiàn)只有葉子節(jié)點的梯度值不為None，這是因為非葉子節(jié)點的梯度值并沒有被保存在內(nèi)存中。

所以葉子節(jié)點是該節(jié)點是否能保存梯度的前提。