【算法】動圖展示八大常用排序算法，一次看個夠！

本文介紹常見的八大排序算法：直接插入排序、希爾排序、選擇排序、堆排序、冒泡排序、快排、歸并排序以及計數(shù)排序

文章內容很干，也很長，不過有多種動圖圖解，希望可以給枯燥的算法學習帶來一抹亮色！

如果對于復雜度還不清楚，可以查看下面的文章

五分鐘復雜度

1冒泡排序

對于冒泡排序相信我們都比較熟悉了，其核心思想就是相鄰元素兩兩比較，把較大的元素放到后面，在一輪比較完成之后，最大的元素就位于最后一個位置了，就好像是氣泡，慢慢的浮出了水面一樣

Java 版實現(xiàn)

public?class?BubbleSort1?{
????public?static?void?BubbleSort(int[]?arr)?{
????????boolean?flag?=?true;
????????while(flag){
????????????int?temp;//定義一個臨時變量
????????????for(int?i=0;i1;i++){//冒泡趟數(shù)，n-1趟
????????????????for(int?j=0;j1;j++){
????????????????????if(arr[j+1]????????????????????????temp?=?arr[j];
????????????????????????arr[j]?=?arr[j+1];
????????????????????????arr[j+1]?=?temp;
????????????????????????flag?=?true;
????????????????????}
????????????????}
????????????????if(!flag){
????????????????????break;//若果沒有發(fā)生交換，則退出循環(huán)
????????????????}
????????????}
????????}
????}
????public?static?void?main(String[]?args)?{
????????int?arr[]?=?new?int[]{1,6,2,2,5};
????????BubbleSort.BubbleSort(arr);
????????System.out.println(Arrays.toString(arr));
????}
}

Python 版實現(xiàn)

def?bubble_sort(data,?reverse=False):
????"""
????:param?data:?list?type?data
????:param?reverse:
????:return:?list?type?data
????"""
????if?not?reverse:
????????for?i?in?range(len(data)?-?1):
????????????for?j?in?range(len(data)?-?1?-i):
????????????????if?data[j]?>?data[j+1]:
????????????????????data[j],?data[j+1]?=?data[j+1],?data[j]
????????return?data
????else:
????????for?i?in?range(len(data)?-?1):
????????????for?j?in?range(len(data)?-?1?-i):
????????????????if?data[j]?1]:
????????????????????data[j],?data[j?+?1]?=?data[j?+?1],?data[j]
????????return?data

冒泡排序算法還是比較好理解的，只需要進行兩次循環(huán)，最外層的循環(huán)代表排序元素的個數(shù)，內部循環(huán)則進行兩兩比較，時間復雜度為 O(n^2)

2快速排序

快排的思想為首先任意選取一個數(shù)據(jù)（通常選用數(shù)組的第一個數(shù)）作為關鍵數(shù)據(jù)，然后將所有比它小的數(shù)都放到它前面，所有比它大的數(shù)都放到它后面，這個過程稱為一趟快速排序，之后再遞歸排序兩邊的數(shù)據(jù)

Jave 版實現(xiàn)

public?class?QuickSort?{
????public?static?void?quickSort(int[]?arr,int?low,int?high){
????????int?i,j,temp,t;
????????if(low>high){
????????????return;
????????}
????????i=low;
????????j=high;
????????//temp就是基準位
????????temp?=?arr[low];
?
????????while?(i????????????//先看右邊，依次往左遞減
????????????while?(temp<=arr[j]&&i????????????????j--;
????????????}
????????????//再看左邊，依次往右遞增
????????????while?(temp>=arr[i]&&i????????????????i++;
????????????}
????????????//如果滿足條件則交換
????????????if?(i????????????????t?=?arr[j];
????????????????arr[j]?=?arr[i];
????????????????arr[i]?=?t;
????????????}
?
????????}
????????//最后將基準為與i和j相等位置的數(shù)字交換
?????????arr[low]?=?arr[i];
?????????arr[i]?=?temp;
????????//遞歸調用左半數(shù)組
????????quickSort(arr,?low,?j-1);
????????//遞歸調用右半數(shù)組
????????quickSort(arr,?j+1,?high);
????}
?
?
????public?static?void?main(String[]?args){
????????int[]?arr?=?{10,7,2,4,7,62,3,4,2,1,8,9,19};
????????quickSort(arr,?0,?arr.length-1);
????????for?(int?i?=?0;?i?????????????System.out.println(arr[i]);
????????}
????}
}

Python 版實現(xiàn)

def?quick_sort(data):
????if?not?data:
????????return?data
????first?=?data[0]
????left?=?quick_sort([l?for?l?in?data[1:]?if?l?????right?=?quick_sort([r?for?r?in?data[1:]?if?r?>=?first])
????return?left?+?[first]?+?right

相比冒泡排序，快速排序每次交換是跳躍式的。每次排序的時候設置一個基準點，將小于等于基準點的數(shù)全部放到基準點的左邊，將大于等于基準點的數(shù)全部放到基準點的右邊。這樣在每次交換的時候就不會像冒泡排序一樣每次只能在相鄰的數(shù)之間進行交換，交換的距離就大的多了。因此總的比較和交換次數(shù)就少了，速度自然就提高了，時間復雜度為 O（N*logN）

3直接插入排序

插入排序的思想是把一個數(shù)據(jù)插入到一個有序序列中，從而得到一個新的序列加一的有序序列，可以通過下圖來進一步加深理解

Java 版實現(xiàn)

public?static?void?InsertSort(int[]?arr)
{
????int?i,?j;
????int?n?=?arr.Length;
????int?target;
?
????//假定第一個元素被放到了正確的位置上
????//這樣，僅需遍歷1?-?n-1
????for?(i?=?1;?i?????{
????????j?=?i;
????????target?=?arr[i];
?
????????while?(j?>?0?&&?target?1])
????????{
????????????arr[j]?=?arr[j?-?1];
????????????j--;
????????}
?
????????arr[j]?=?target;
????}
}

Python 版實現(xiàn)

def?insert_sort(data,?reverse=False):
????if?not?reverse:
????????for?i?in?range(1,?len(data)):
????????????key?=?data[i]
????????????j?=?i?-?1
????????????while?j?>=?0:
????????????????if?data[j]?>?key:
????????????????????data[j+1]?=?data[j]
????????????????????data[j]?=?key
????????????????j?-=?1
????????return?data
????else:
????????for?i?in?range(1,?len(data)):
????????????key?=?data[i]
????????????j?=?i?-?1
????????????while?j?>=?0:
????????????????if?data[j]?????????????????????data[j+1]?=?data[j]
????????????????????data[j]?=?key
????????????????j?-=?1
????????return?data

由于每次遍歷有序序列時，都會有序列中所有的數(shù)據(jù)做對比，故而時間復雜度為O(n^2)

4選擇排序

選擇排序，是逐個確定元素位置的思想。同樣是 n 遍循環(huán)，第一輪時，每一個元素都與第一個元素比較，如果比第一個元素大，則與之交換，這樣一輪過后，第一個元素就是最小的了，第二輪開始每個元素與第二個位置的元素比較，如果大，則與第二位置的元素交換，以此類推，達到排序的目的

Java 版實現(xiàn)

public?static?int[]?selectionSort(int[]?array)?{
????int?len?=?array.length;
????//?如果數(shù)組長度為0或者1，都是不用排序直接返回
????if(len?==?0?||?len?==?1)?{
????????return?array;
????}
????for(int?i?=?0;?i?1;?i++)?{
????????int?minIdx?=?i;
????????for(int?j?=?i?+?1;?j?????????????//?找到最小的數(shù)
????????????if(array[minIdx]?>?array[j])?{
????????????????//?保存最小數(shù)的索引
????????????????minIdx?=?j;
????????????}
????????}
????????//?如果一輪比較下來都沒有變更最小值的索引則無需調換順序
????????if(minIdx?!=?i)?{
????????????int?tmp?=?array[i];
????????????array[i]?=?array[minIdx];
????????????array[minIdx]?=?tmp;
????????}
????}
????return?array;
}

Python 版實現(xiàn)

def?selection_sort(data,?reverse=False):
????"""
????:param?data:?list?type?data
????:param?reverse:
????:return:?list?type?data
????"""
????if?not?reverse:
????????for?i?in?range(len(data)-1):
????????????min_index?=?i
????????????for?j?in?range(i+1,?len(data)):
????????????????if?data[j]?????????????????????min_index?=?j
????????????data[i],?data[min_index]?=?data[min_index],?data[i]
????????return?data
????else:
????????for?i?in?range(len(data)?-?1):
????????????min_index?=?i
????????????for?j?in?range(i+1,?len(data)):
????????????????if?data[j]?>?data[min_index]:
????????????????????min_index?=?j
????????????data[i],?data[min_index]?=?data[min_index],?data[i]
????????return?data

選擇排序和冒泡排序還是很相似的，但是選擇排序會比冒泡排序少一次交換的過程，但是同樣是兩層循環(huán)，所有時間復雜度也是 O(n^2)

5并歸排序

可以把一個數(shù)組分成兩半，對于每一個數(shù)組當他們是有序的就可以進行一次合并操作。對于他們的兩個區(qū)間進行遞歸，一直遞歸下去劃分區(qū)間，當區(qū)間只有一個值的時候我們就可以進行合并返回上一層，讓上一層合并再返回

Java 版實現(xiàn)

public?static?int[]?sort(int[]?a,int?low,int?high){
????????int?mid?=?(low+high)/2;
????????if(low????????????sort(a,low,mid);
????????????sort(a,mid+1,high);
????????????//左右歸并
????????????merge(a,low,mid,high);
????????}
????????return?a;
????}
?????
????public?static?void?merge(int[]?a,?int?low,?int?mid,?int?high)?{
????????int[]?temp?=?new?int[high-low+1];
????????int?i=?low;
????????int?j?=?mid+1;
????????int?k=0;
????????//?把較小的數(shù)先移到新數(shù)組中
????????while(i<=mid?&&?j<=high){
????????????if(a[i]????????????????temp[k++]?=?a[i++];
????????????}else{
????????????????temp[k++]?=?a[j++];
????????????}
????????}
????????//?把左邊剩余的數(shù)移入數(shù)組?
????????while(i<=mid){
????????????temp[k++]?=?a[i++];
????????}
????????//?把右邊邊剩余的數(shù)移入數(shù)組
????????while(j<=high){
????????????temp[k++]?=?a[j++];
????????}
????????//?把新數(shù)組中的數(shù)覆蓋nums數(shù)組
????????for(int?x=0;x????????????a[x+low]?=?temp[x];
????????}
????}

Python 版實現(xiàn)

def?merge(a,?b):
????c?=?[]
????h?=?j?=?0
????while?j?and?h?????????if?a[j]?????????????c.append(a[j])
????????????j?+=?1
????????else:
????????????c.append(b[h])
????????????h?+=?1
?
????if?j?==?len(a):
????????for?i?in?b[h:]:
????????????c.append(i)
????else:
????????for?i?in?a[j:]:
????????????c.append(i)
?
????return?c
?
?
def?merge_sort(lists):
????if?len(lists)?<=?1:
????????return?lists
????middle?=?len(lists)//2
????left?=?merge_sort(lists[:middle])
????right?=?merge_sort(lists[middle:])
????return?merge(left,?right)

歸并排序采用分而治之的原理：首先將一個序列從中間位置分成兩個序列，然后再將這兩個子序列按照第一步繼續(xù)二分下去，最后直到所有子序列的長度都為1，也就是不可以再二分截止。這時候再兩兩合并成一個有序序列即可。時間復雜度 O（NlogN)

6隨機快速排序

隨機快速排序與快速排序的思路一樣，差異就是取主元之前，隨機快速排序多了一個步驟：隨機快速排序是隨機取得一個元素，并且會與最后一個元素交換位置。取得主元的下標位置實際上還是最后一個下標，快速排序是習慣取得最后一個元素作為主元

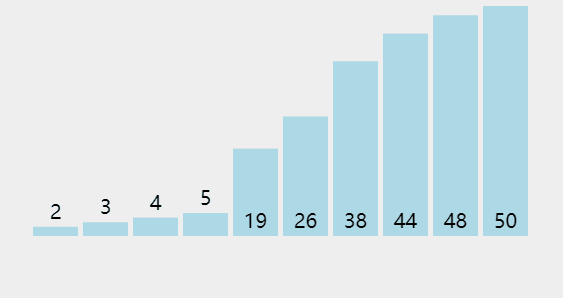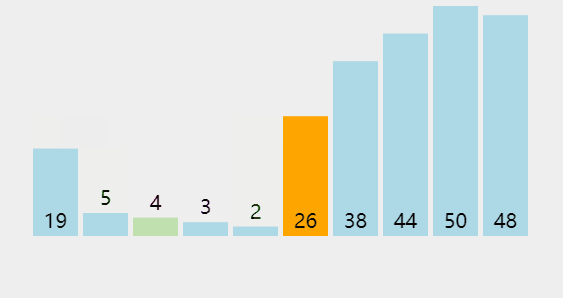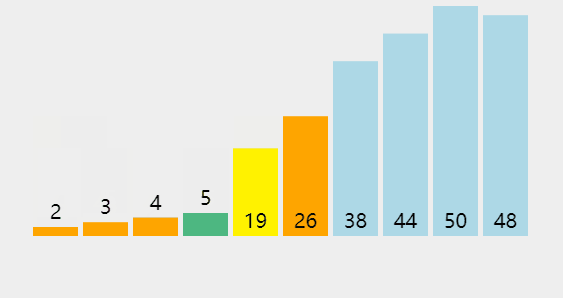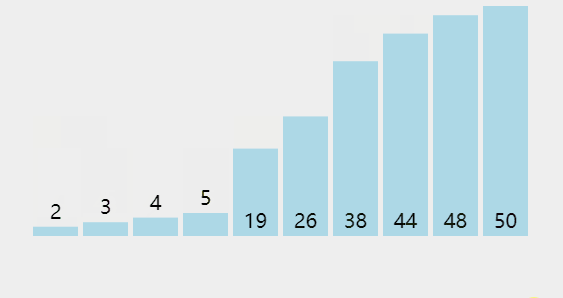
Java 版實現(xiàn)

package?quicksort;

import?java.util.Random;

public?class?RandomQuickSort?{

????public?void?Sort(int[]?a,?int?p,?int?r)?{
????????if?(p?????????????int?q?=?Partition(a,?p,?r);
????????????Sort(a,?p,?q-1);
????????????Sort(a,q+1,?r);
????????}
????}

????private?int?Partition(int[]?A,?int?p,?int?r)?{
????????/*隨機選取主元元素*/
????????Random?random?=?new?Random();
????????int?random_index?=?random.nextInt(r-p+1)+p;
????????System.out.println("random_index="+random_index);
????????int?temp?=?A[random_index];
????????A[random_index]?=?A[r];
????????A[r]?=?temp;

????????int?x?=?A[r];??//pivot?=?A[p]
????????int?i?=?p-1;
????????for?(int?j?=?p;?j?????????????if?(A[j]?<=?x)?{??//與pivot作比較
????????????????i++;
????????????????int?tmp?=?A[j];
????????????????A[j]?=?A[i];
????????????????A[i]?=?tmp;
????????????}
????????}

????????int?tmp?=?A[r];
????????A[r]?=?A[i+1];
????????A[i+1]?=?tmp;

????????return?i+1;

????}

}

Python 版實現(xiàn)

import?random
def?random_quicksort(a,left,right):
????if(left????????mid?=?random_partition(a,left,right)
????????random_quicksort(a,left,mid-1)
????????random_quicksort(a,mid+1,right)


def?random_partition(a,left,right):?
????t?=?random.randint(left,right)?????#生成[left,right]之間的一個隨機數(shù)
????a[t],a[right]?=?a[right],a[t]????
????x?=?a[right]
????i?=?left-1?????????????????????????#初始i指向一個空，保證0到i都小于等于?x
????for?j?in?range(left,right):????????#j用來尋找比x小的，找到就和i+1交換，保證i之前的都小于等于x
????????if(a[j]<=x):
????????????i?=?i+1
????????????a[i],a[j]?=?a[j],a[i]
????a[i+1],a[right]?=?a[right],a[i+1]??#0到i?都小于等于x?,所以x的最終位置就是i+1
????return?i+1

while(True):
????try:
????????s?=?input("輸入待排序數(shù)組：\n")?????????????#待排數(shù)組
????????l?=s.split()
????????a?=?[int(t)?for?t?in?l]
????????random_quicksort(a,0,len(a)-1)
????????print?("排序后：")
????????for?item?in?a:
????????????print(item,end=‘?‘)
????????print("\n")
????except:
????????break

7計數(shù)排序

首先統(tǒng)計原數(shù)組中每個值出現(xiàn)的次數(shù)

然后進行排序：遍歷Count數(shù)組，對應位置的值出現(xiàn)多少次就往原數(shù)組寫幾個這個值

當然，在對于數(shù)據(jù)比較大的時候我們可以通過相對映射，讓（該值-min）后的數(shù)組加一，最后還原回去即可

Java 版實現(xiàn)

public?static?int[]?CountingSort(int[]?a)?{
????int?b[]?=?new?int[a.length];
????int?max?=?a[0],?min?=?a[0];
????for?(int?i=1;i????????if?(a[i]?>?max)?{
????????????max?=?a[i];
????????}
????????if?(a[i]?????????min?=?a[i];
????????}
????}?
????//?k的大小是要排序的數(shù)組中，元素大小的極值差+1
????int?k?=?max?-?min?+?1;
????int?c[]?=?new?int[k];
????//統(tǒng)計A數(shù)組元素出現(xiàn)次數(shù)
????for?(int?i?=?0;?i?????????c[a[i]?-?min]?+=?1;
????}
????//更新計算C數(shù)組
????for?(int?i?=?1;?i?????????c[i]?=?c[i]?+?c[i?-?1];
????}
????//填充B數(shù)組
????for?(int?i?=?a.length?-?1;?i?>=?0;?--i)?{
????????b[--c[a[i]?-?min]]?=?a[i];
????}
????return?b;
}

Python 版實現(xiàn)

def?countSort(arr):
????max_value?=?max(arr)
????res?=?[]
????count_nums?=?[0?for?i?in?range(max_value?+?1)]
????for?num?in?arr:
????????count_nums[num]?+=?1
????for?i?in?range(len(count)):
????????if?count_nums[i]?!=?0:
#?元素i有?count_nums[i]個，添加入最終的排序數(shù)組
????????????res.extend(count_nums[i]?*?[i])
????return?res

8基數(shù)排序

基數(shù)排序核心思想是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次類推，直到最高位。有時候有些屬性是有優(yōu)先級順序的，先按低優(yōu)先級排序，再按高優(yōu)先級排序。最后的次序就是高優(yōu)先級高的在前，高優(yōu)先級相同的低優(yōu)先級高的在前

Java 版實現(xiàn)

public?class?RadixSort?{
????public?static?void?main(String[]?args)?{
????????int[]?arr?=?{63,?157,?189,?51,?101,?47,?141,?121,?157,?156,
????????????????194,?117,?98,?139,?67,?133,?181,?12,?28,?0,?109};

????????radixSort(arr);

????????System.out.println(Arrays.toString(arr));
????}

????/**
?????*?高位優(yōu)先法
?????*
?????*?@param?arr?待排序列，必須為自然數(shù)
?????*/
????private?static?void?radixSort(int[]?arr)?{
????????//待排序列最大值
????????int?max?=?arr[0];
????????int?exp;//指數(shù)

????????//計算最大值
????????for?(int?anArr?:?arr)?{
????????????if?(anArr?>?max)?{
????????????????max?=?anArr;
????????????}
????????}

????????//從個位開始，對數(shù)組進行排序
????????for?(exp?=?1;?max?/?exp?>?0;?exp?*=?10)?{
????????????//存儲待排元素的臨時數(shù)組
????????????int[]?temp?=?new?int[arr.length];
????????????//分桶個數(shù)
????????????int[]?buckets?=?new?int[10];

????????????//將數(shù)據(jù)出現(xiàn)的次數(shù)存儲在buckets中
????????????for?(int?value?:?arr)?{
????????????????//(value?/?exp)?%?10?:value的最底位(個位)
????????????????buckets[(value?/?exp)?%?10]++;
????????????}

????????????//更改buckets[i]，
????????????for?(int?i?=?1;?i?10;?i++)?{
????????????????buckets[i]?+=?buckets[i?-?1];
????????????}

????????????//將數(shù)據(jù)存儲到臨時數(shù)組temp中
????????????for?(int?i?=?arr.length?-?1;?i?>=?0;?i--)?{
????????????????temp[buckets[(arr[i]?/?exp)?%?10]?-?1]?=?arr[i];
????????????????buckets[(arr[i]?/?exp)?%?10]--;
????????????}

????????????//將有序元素temp賦給arr
????????????System.arraycopy(temp,?0,?arr,?0,?arr.length);
????????}

????}
}

Python 版實現(xiàn)

def?radixSort(arr):
????n?=?len(str(max(arr)))??#?記錄最大值的位數(shù)
????for?k?in?range(n):#n輪排序
????????#?每一輪生成10個列表
????????bucket_list=[[]?for?i?in?range(10)]#因為每一位數(shù)字都是0~9，故建立10個桶
????????for?i?in?arr:
????????????#?按第k位放入到桶中
????????????bucket_list[i//(10**k)%10].append(i)
????????#?按當前桶的順序重排列表
????????arr=[j?for?i?in?bucket_list?for?j?in?i]
????return?arr

今天我們的排序算法就介紹到這里，后面我們還會更加深入的介紹其他數(shù)據(jù)結構和算法，不要錯過哦