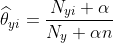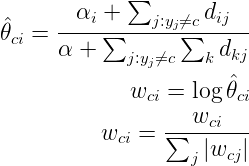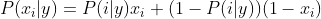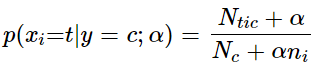大家好，我是愛(ài)生活，AI風(fēng)控的小伍哥，今天給大家?guī)?lái)的文章，關(guān)于樸素貝葉斯的，一個(gè)古老而經(jīng)典的算法，充分的理解有利于對(duì)風(fēng)控特征或者識(shí)別的開(kāi)拓新的思路。
一、從一個(gè)案例講起
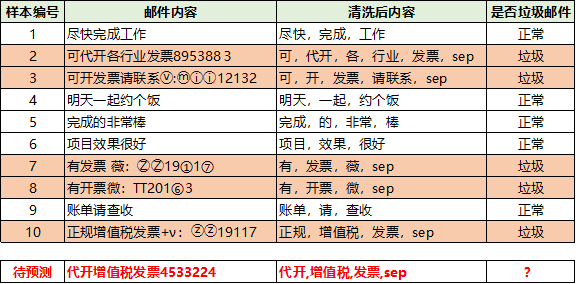
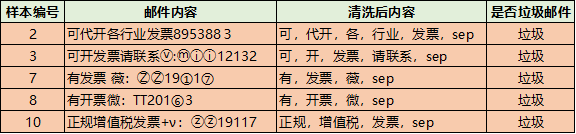
假如我們的目標(biāo)是判斷郵件是否是垃圾郵件，郵件內(nèi)容是【代開(kāi)增值稅發(fā)票4533224】，那么我們要怎么做呢？回憶下高中的數(shù)學(xué)知識(shí)，數(shù)學(xué)原理貝葉斯公式:?P(Y|X) = P(X|Y) * P(Y) / P(X)當(dāng)X條件獨(dú)立時(shí)：P(X|Y) = P(X1|Y) * P(X2|Y) * ...*P(Xn|Y)把該公式，應(yīng)用到我們的風(fēng)險(xiǎn)識(shí)別上，可以得到如下的公式到這一步，上面的 ?P(Text="代開(kāi)增值稅發(fā)票4533224") 是算不出來(lái)的，我們進(jìn)一步處理，這樣分母就自己約掉了于是，我們只要計(jì)算分子的值就可以，下面的幾個(gè)值，都是可以根據(jù)訓(xùn)練集進(jìn)行計(jì)算的就這樣，我們把公式和實(shí)際的應(yīng)用聯(lián)系起來(lái)了。并且每個(gè)指標(biāo)都是可以計(jì)算的。當(dāng)然要計(jì)算上面的概率，需要我們有歷史數(shù)據(jù)，于是我從我的郵箱里面復(fù)制了一些垃圾郵件，以及一些正常的郵件，并對(duì)數(shù)據(jù)做了一下簡(jiǎn)單的預(yù)處理處理，打上了垃圾郵件和正常郵件的標(biāo)簽，我們就可以得到歷史數(shù)據(jù)，進(jìn)行計(jì)算了。P（代開(kāi)|垃圾） ? = 1/5 ?= 0.2P（發(fā)票|垃圾） ? = 4/5 = 0.8計(jì)算垃圾郵件的概率，一共10個(gè)樣本，5個(gè)垃圾郵件，5個(gè)正常郵件垃圾郵件的分子 = 0.2*0.2*0.8*1.0*0.5 = 0.0160000但是每個(gè)都是0，我們要做下拉普拉斯變換（分子分母分別加1，嚴(yán)格的拉普拉斯并不是這樣的，這里簡(jiǎn)化計(jì)算了），采用拉普拉斯變換計(jì)算得到,具體定義見(jiàn)后文，專門解決0概率問(wèn)題：P（代開(kāi)|正常） ? = 1/（5+1） ?= 0.167P（增值稅|正常）= 1/（5+1） ?= ?0.167P（發(fā)票|正常） ? ?= 1/（5+1） = ?0.167P（sep|正常） ? ? = 1/（5+1） = ?0.167計(jì)算垃圾郵件的概率，一共10個(gè)樣本，5個(gè)垃圾郵件，5個(gè)正常郵件正常郵件的分子 = 0.167*0.167*0.167*0.167*0.5 = 0.0003889最后的結(jié)果（雖然拉普拉斯不大嚴(yán)謹(jǐn)，但是計(jì)算過(guò)程沒(méi)問(wèn)題）P（垃圾|代開(kāi),增值稅,發(fā)票,sep） = ??0.0160000/(0.0160000+0.0003889)?= 0.976271P（正常|代開(kāi),增值稅,發(fā)票,sep） = ??0.0003889/(0.0160000+0.0003889) = 0.023729我們計(jì)算下正常郵件的概率為多大，按公式直接計(jì)算，結(jié)果為0，但是直接計(jì)算，會(huì)導(dǎo)致很多樣本都為0，所以后面會(huì)引入拉普拉斯平滑。P（正常|代開(kāi),增值稅,發(fā)票,sep） = 0當(dāng)然我，我們用Python內(nèi)置的庫(kù)，就更簡(jiǎn)單了，幾行代碼就搞定了。data = ['盡快，完成，工作', '可，代開(kāi)，各，行業(yè)，發(fā)票，sep', '可，開(kāi)，發(fā)票，請(qǐng)聯(lián)系，sep',????'明天，一起，約個(gè)飯', '完成，的，非常，棒', '項(xiàng)目，效果，很好', '有，發(fā)票，薇，sep', '有，開(kāi)票，微，sep', '賬單，請(qǐng)，查收', '正規(guī)，增值稅，發(fā)票，sep']label=[0,1,1,0,0,0,1,1,0,1]vectorizer_word = TfidfVectorizer()vectorizer_word.fit(data,)train = vectorizer_word.transform(data)test = vectorizer_word.transform(['代開(kāi),增值稅,發(fā)票,sep'])from sklearn.naive_bayes import BernoulliNBclf = BernoulliNB()clf.fit(train.toarray(), label)clf.predict(test.toarray(),)clf.predict_proba(test.toarray(),)array([[0.00154805, 0.99845195]])算出來(lái)的概率也是0.99845195左右，和我們手動(dòng)計(jì)算的差不多
二、貝葉斯定理概述
貝葉斯定理由英國(guó)數(shù)學(xué)家貝葉斯 ( Thomas Bayes 1702-1761 ) 發(fā)展，用來(lái)描述兩個(gè)條件概率之間的關(guān)系，比如 P(A|B) 和 P(B|A)。主要用于文本分類。樸素貝葉斯法是基于貝葉斯定理與特征條件獨(dú)立假設(shè)的分類方法。貝葉斯定理太有用了，不管是在投資領(lǐng)域，還是機(jī)器學(xué)習(xí)，或是日常生活中高手幾乎都在用到它。
生命科學(xué)家用貝葉斯定理研究基因是如何被控制的，教育學(xué)家意識(shí)到,學(xué)生的學(xué)習(xí)過(guò)程其實(shí)就是貝葉斯法則的運(yùn)用，基金經(jīng)理用貝葉斯法則找到投資策略，谷歌用貝葉斯定理改進(jìn)搜索功能，幫助用戶過(guò)濾垃圾郵件，無(wú)人駕駛汽車接收車頂傳感器收集到的路況和交通數(shù)據(jù)運(yùn)用貝葉斯定理更新從地圖上獲得的信息，人工智能、機(jī)器翻譯中大量用到貝葉斯定理，比如肝癌的檢測(cè)、垃圾郵件的過(guò)濾。樸素貝葉斯分類（NBC）是以貝葉斯定理為基礎(chǔ)并且假設(shè)特征條件之間相互獨(dú)立的方法，先通過(guò)已給定的訓(xùn)練集，以特征詞之間獨(dú)立作為前提假設(shè)，學(xué)習(xí)從輸入到輸出的聯(lián)合概率分布，再基于學(xué)習(xí)到的模型，輸入X求出使得后驗(yàn)概率最大的輸出Y 。?設(shè)有樣本數(shù)據(jù)集D={d1,d2,...,dn}，對(duì)應(yīng)樣本數(shù)據(jù)的特征屬性集為X={x1,x2,...,xd}類變量為Y={y1,y2,...ym}?，即D可以分為ym類別。其中{x1,x2,...,xd}?相互獨(dú)立且隨機(jī)，則Y的先驗(yàn)概率P(Y)?，Y的后驗(yàn)概率P(Y|X)?，由樸素貝葉斯算法可得，后驗(yàn)概率可以由先驗(yàn)概率P(Y) ,證據(jù)P(X) ,類條件概率P(X|Y)計(jì)算出樸素貝葉斯基于各特征之間相互獨(dú)立，在給定類別為y的情況下，上式可以進(jìn)一步表示為下式：由以上兩式可以計(jì)算出后驗(yàn)概率為：由于P(X)的大小是固定不變的，因此在比較后驗(yàn)概率時(shí)，只比較上式的分子部分即可,因此可以得到一個(gè)樣本數(shù)據(jù)屬于類別yi的樸素貝葉斯計(jì)算：對(duì)于上述例題，就得到如下的表達(dá)式?
零概率問(wèn)題：即測(cè)試樣例的標(biāo)簽屬性中，出現(xiàn)了模型訓(xùn)練過(guò)程中沒(méi)有記錄的值，或者某個(gè)分類沒(méi)有記錄的值，從而出現(xiàn)該標(biāo)簽屬性值的出現(xiàn)概率?P(wi|Ci) = 0?的現(xiàn)象。因?yàn)?P(w|Ci) 等于各標(biāo)簽屬性值 P(wi|Ci) 的乘積，當(dāng)分類 Ci 中某一個(gè)標(biāo)簽屬性值的概率為 0，最后的 P(w|Ci) 結(jié)果也為 0。很顯然，這不能真實(shí)地代表該分類出現(xiàn)的概率解決方法：拉普拉斯修正，又叫拉普拉斯平滑，這是為了解決零概率問(wèn)題而引入的處理方法。其修正過(guò)程：浮點(diǎn)數(shù)溢出問(wèn)題：在計(jì)算 P(w|Ci) 時(shí)，各標(biāo)簽屬性概率的值可能很小，而很小的數(shù)再相乘，可能會(huì)導(dǎo)致浮點(diǎn)數(shù)溢出。解決方法：對(duì) P(w|Ci) 取對(duì)數(shù)，把概率相乘轉(zhuǎn)換為相加。對(duì)于離散型變量，直接統(tǒng)計(jì)頻數(shù)分布就可以了。對(duì)于連續(xù)型的變量，為了計(jì)算對(duì)應(yīng)的概率，此時(shí)又引入了一個(gè)假設(shè)，假設(shè)特征的分布為正態(tài)分布，計(jì)算樣本的均值和方差，然后通過(guò)密度函數(shù)計(jì)算取值時(shí)對(duì)應(yīng)的概率從上面的例子可以看出，樸素貝葉斯假設(shè)樣本特征相互獨(dú)立，而且連續(xù)型的特征分布符合正態(tài)分布，這樣的假設(shè)前提是比較理想化的，所以稱之為"樸素"貝葉斯，因?yàn)閷?shí)際數(shù)據(jù)并不一定會(huì)滿足這樣的要求。在scikit-learn庫(kù)，根據(jù)特征數(shù)據(jù)的先驗(yàn)分布不同，給我們提供了5種不同的樸素貝葉斯分類算法（sklearn.naive_bayes: Naive Bayes模塊），分別是伯努利樸素貝葉斯（BernoulliNB），類樸素貝葉斯（CategoricalNB），高斯樸素貝葉斯（GaussianNB）、多項(xiàng)式樸素貝葉斯（MultinomialNB）、補(bǔ)充樸素貝葉斯（ComplementNB） 。 | Naive Bayes classifier for multivariate Bernoulli models. |
| naive_bayes.CategoricalNB | Naive Bayes classifier for categorical features |
| The Complement Naive Bayes classifier described in Rennie et al. |
| Gaussian Naive Bayes (GaussianNB) |
| naive_bayes.MultinomialNB | Naive Bayes classifier for multinomial models |
這5種算法適合應(yīng)用在不同的數(shù)據(jù)場(chǎng)景下，我們應(yīng)該根據(jù)特征變量的不同選擇不同的算法，下面是一些常規(guī)的區(qū)別和介紹。高斯樸素貝葉斯，特征變量是連續(xù)變量，符合高斯分布，比如說(shuō)人的身高，物體的長(zhǎng)度。特征變量是離散變量，符合多項(xiàng)分布，在文檔分類中特征變量體現(xiàn)在一個(gè)單詞出現(xiàn)的次數(shù)，或者是單詞的 TF-IDF 值等。不支持負(fù)數(shù)，所以輸入變量特征的時(shí)候，別用StandardScaler進(jìn)行標(biāo)準(zhǔn)化數(shù)據(jù)，可以使用MinMaxScaler進(jìn)行歸一化。這個(gè)模型假設(shè)特征復(fù)合多項(xiàng)式分布，是一種非常典型的文本分類模型，模型內(nèi)部帶有平滑參數(shù)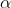
。是MultinomialNB模型的一個(gè)變種，實(shí)現(xiàn)了補(bǔ)碼樸素貝葉斯(CNB)算法。CNB是標(biāo)準(zhǔn)多項(xiàng)式樸素貝葉斯(MNB)算法的一種改進(jìn)，比較適用于不平衡的數(shù)據(jù)集，在文本分類上的結(jié)果通常比MultinomialNB模型好，具體來(lái)說(shuō)，CNB使用來(lái)自每個(gè)類的補(bǔ)數(shù)的統(tǒng)計(jì)數(shù)據(jù)來(lái)計(jì)算模型的權(quán)重。CNB的發(fā)明者的研究表明，CNB的參數(shù)估計(jì)比MNB的參數(shù)估計(jì)更穩(wěn)定。模型適用于多元伯努利分布，即每個(gè)特征都是二值變量，如果不是二值變量，該模型可以先對(duì)變量進(jìn)行二值化，在文檔分類中特征是單詞是否出現(xiàn)，如果該單詞在某文件中出現(xiàn)了即為1，否則為0。在文本分類的示例中，統(tǒng)計(jì)詞語(yǔ)是否出現(xiàn)的向量(word occurrence vectors)(而非統(tǒng)計(jì)詞語(yǔ)出現(xiàn)次數(shù)的向量(word count vectors))可以用于訓(xùn)練和使用這個(gè)分類器。BernoulliNB 可能在一些數(shù)據(jù)集上表現(xiàn)得更好，特別是那些更短的文檔。如果時(shí)間允許，建議對(duì)兩個(gè)模型都進(jìn)行評(píng)估。對(duì)分類分布的數(shù)據(jù)實(shí)施分類樸素貝葉斯算法，專用于離散數(shù)據(jù)集， 它假定由索引描述的每個(gè)特征都有其自己的分類分布。對(duì)于訓(xùn)練集中的每個(gè)特征 X，CategoricalNB估計(jì)以類y為條件的X的每個(gè)特征i的分類分布。樣本的索引集定義為J=1,…,m，m作為樣本數(shù)。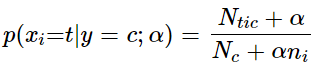
案例測(cè)試from sklearn.naive_bayes import MultinomialNB,GaussianNB,BernoulliNB,ComplementNB from sklearn.datasets import load_breast_cancerfrom sklearn.model_selection import cross_val_scoreX,y = load_breast_cancer().data,load_breast_cancer().targetnb1= GaussianNB()nb2= MultinomialNB()nb3= BernoulliNB()nb4= ComplementNB()for model in [nb1,nb2,nb3,nb4]: scores=cross_val_score(model,X,y,cv=10,scoring='accuracy')????print("Accuracy:{:.4f}".format(scores.mean()))Accuracy:0.9368Accuracy:0.8928Accuracy:0.6274Accuracy:0.8928
from sklearn.naive_bayes import MultinomialNB,GaussianNB,BernoulliNB,ComplementNB ,CategoricalNBfrom sklearn.datasets import load_irisfrom sklearn.model_selection import cross_val_scoreX,y = load_iris().data,load_iris().targetgn1 = GaussianNB()gn2 = MultinomialNB()gn3 = BernoulliNB() gn4 = ComplementNB()gn5 = CategoricalNB(alpha=1)for model in [gn1,gn2,gn3,gn4,gn5]: scores = cross_val_score(model,X,y,cv=10,scoring='accuracy') print("Accuracy:{:.4f}".format(scores.mean()))Accuracy:0.9533Accuracy:0.9533Accuracy:0.3333Accuracy:0.6667Accuracy:0.9267
進(jìn)行one-hot變化，可以發(fā)現(xiàn)BernoulliNB分類準(zhǔn)確率還是很高的from sklearn import preprocessing enc = preprocessing.OneHotEncoder() # 創(chuàng)建對(duì)象from sklearn.datasets import load_irisX,y = load_iris().data,load_iris().target
enc.fit(X) array = enc.transform(X).toarray()
from sklearn.naive_bayes import MultinomialNB,GaussianNB,BernoulliNB,ComplementNB ,CategoricalNBfrom sklearn.datasets import load_irisfrom sklearn.model_selection import cross_val_scoreX,y = load_iris().data,load_iris().targetgn1 = GaussianNB()gn2 = MultinomialNB()gn3 = BernoulliNB()gn4 = ComplementNB()for model in [gn1,gn2,gn3,gn4]: scores=cross_val_score(model,array,y,cv=10,scoring='accuracy') print("Accuracy:{:.4f}".format(scores.mean()))Accuracy:0.8933Accuracy:0.9333Accuracy:0.9333Accuracy:0.9400
長(zhǎng)按關(guān)注公眾號(hào)? ?? ? ? ??長(zhǎng)按加作者好友
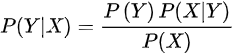
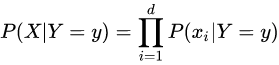
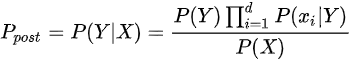
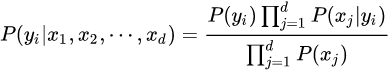
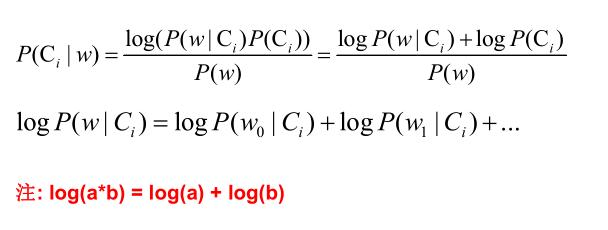
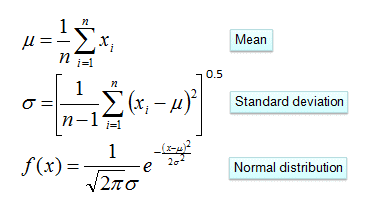
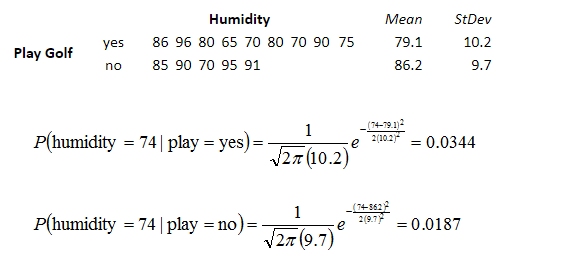
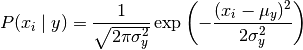
