超詳細(xì)圖解Self-Attention的那些事兒

來源:NewBeenNLP 本文約3000字,建議閱讀6分鐘
本文教你OKV矩陣輕松理解。
向量的內(nèi)積是什么,如何計(jì)算,最重要的,其幾何意義是什么?
一個(gè)矩陣
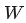 與其自身的轉(zhuǎn)置相乘,得到的結(jié)果有什么意義?
與其自身的轉(zhuǎn)置相乘,得到的結(jié)果有什么意義?
1. 鍵值對(duì)注意力
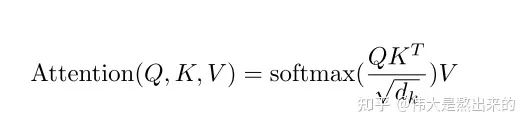
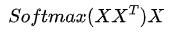
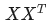 代表什么?
代表什么?
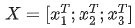 ?,其中X?為一個(gè)二維矩陣,?
?,其中X?為一個(gè)二維矩陣,?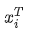 為一個(gè)行向量(其實(shí)很多教材都默認(rèn)向量是列向量,為了方便舉例請(qǐng)讀者理解筆者使用行向量)。對(duì)應(yīng)下面的圖,
為一個(gè)行向量(其實(shí)很多教材都默認(rèn)向量是列向量,為了方便舉例請(qǐng)讀者理解筆者使用行向量)。對(duì)應(yīng)下面的圖,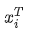 對(duì)應(yīng)"早"字embedding之后的結(jié)果,以此類推。
對(duì)應(yīng)"早"字embedding之后的結(jié)果,以此類推。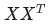 ?。我們來看看其結(jié)果究竟有什么意義
?。我們來看看其結(jié)果究竟有什么意義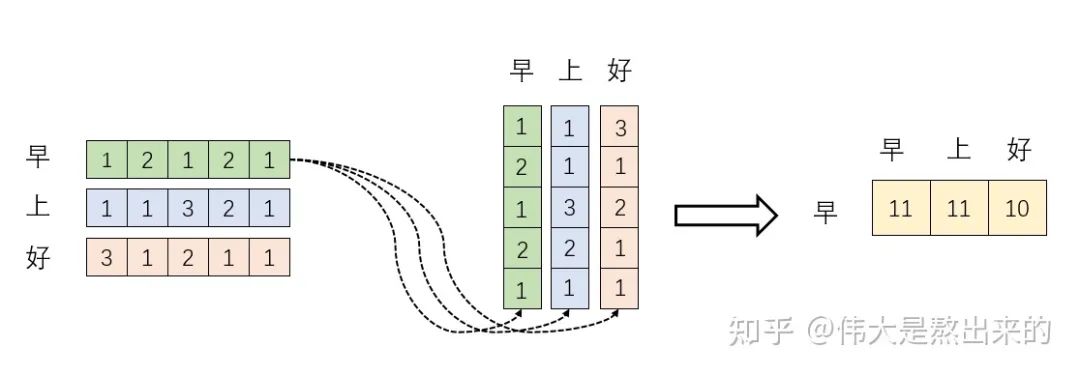
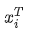 分別與自己和其他兩個(gè)行向量做內(nèi)積("早"分別與"上""好"計(jì)算內(nèi)積),得到了一個(gè)新的向量。我們回想前文提到的向量的內(nèi)積表征兩個(gè)向量的夾角,表征一個(gè)向量在另一個(gè)向量上的投影。那么新的向量向量有什么意義的?是行向量
分別與自己和其他兩個(gè)行向量做內(nèi)積("早"分別與"上""好"計(jì)算內(nèi)積),得到了一個(gè)新的向量。我們回想前文提到的向量的內(nèi)積表征兩個(gè)向量的夾角,表征一個(gè)向量在另一個(gè)向量上的投影。那么新的向量向量有什么意義的?是行向量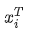 在自己和其他兩個(gè)行向量上的投影。我們思考,投影的值大有什么意思?投影的值小又如何?
在自己和其他兩個(gè)行向量上的投影。我們思考,投影的值大有什么意思?投影的值小又如何?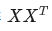 的意義是什么呢?
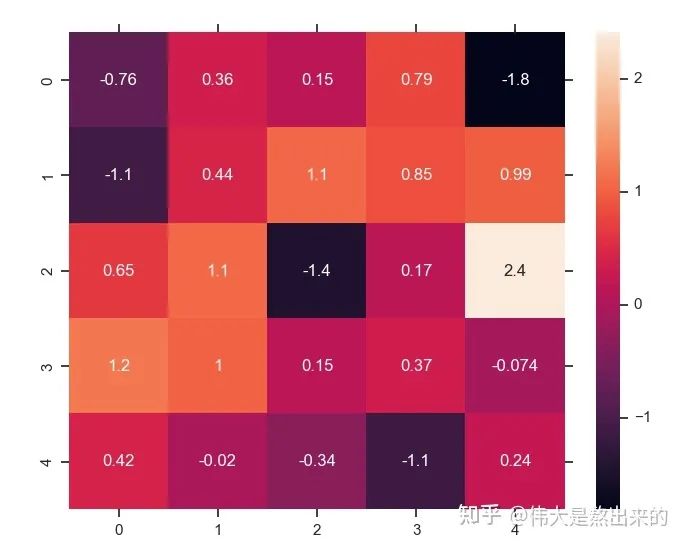
的意義是什么呢?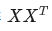 ?是一個(gè)方陣,我們以行向量的角度理解,里面保存了每個(gè)向量與自己和其他向量進(jìn)行內(nèi)積運(yùn)算的結(jié)果。
?是一個(gè)方陣,我們以行向量的角度理解,里面保存了每個(gè)向量與自己和其他向量進(jìn)行內(nèi)積運(yùn)算的結(jié)果。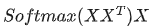 中,
中,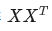 的意義。我們進(jìn)一步,Softmax的意義何在呢?請(qǐng)看下圖
的意義。我們進(jìn)一步,Softmax的意義何在呢?請(qǐng)看下圖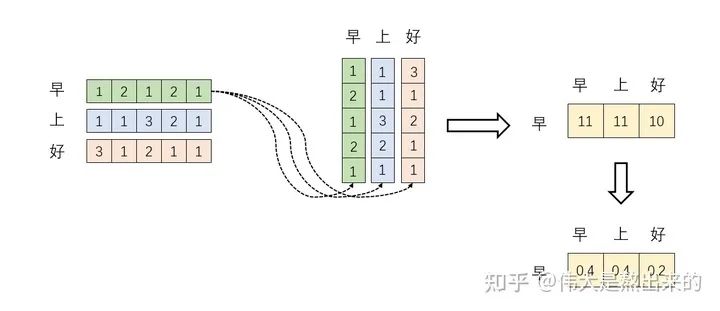
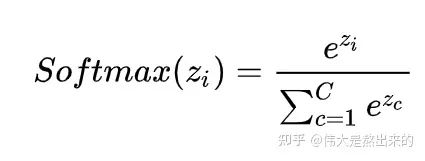
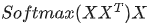 已經(jīng)理解了其中的一半。最后一個(gè) X 有什么意義?完整的公式究竟表示什么?我們繼續(xù)之前的計(jì)算,請(qǐng)看下圖
已經(jīng)理解了其中的一半。最后一個(gè) X 有什么意義?完整的公式究竟表示什么?我們繼續(xù)之前的計(jì)算,請(qǐng)看下圖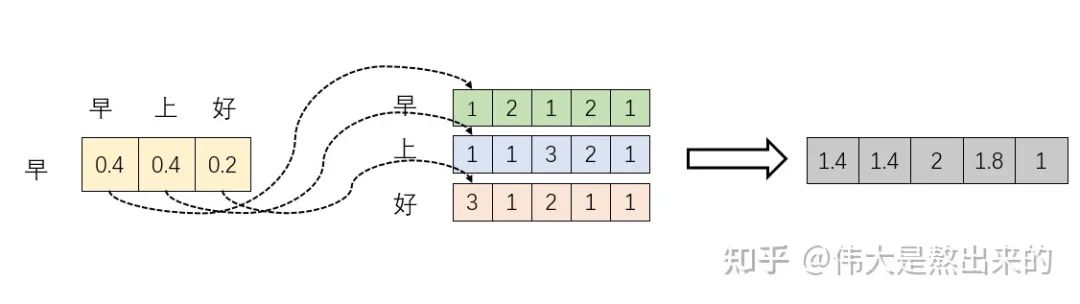
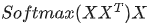 的一個(gè)行向量舉例。這一行向量與X的一個(gè)列向量相乘,表示什么?
的一個(gè)行向量舉例。這一行向量與X的一個(gè)列向量相乘,表示什么?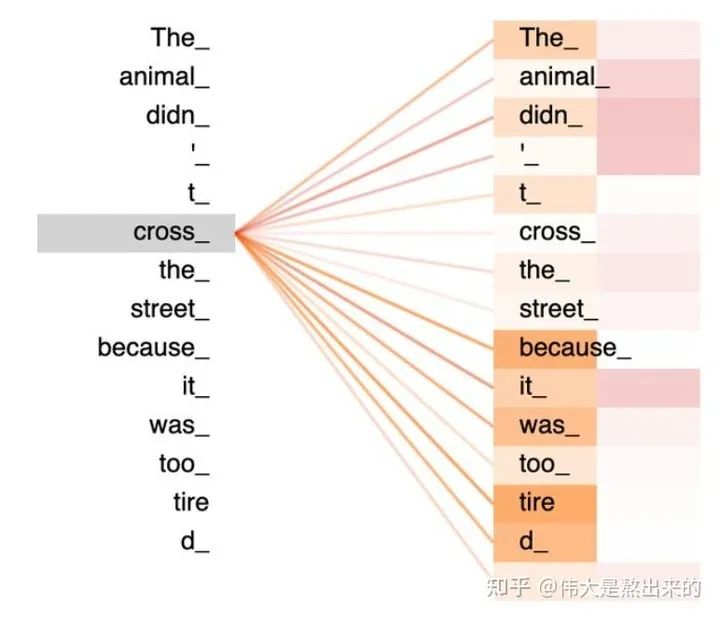
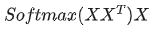 已經(jīng)有了更深刻的理解。
已經(jīng)有了更深刻的理解。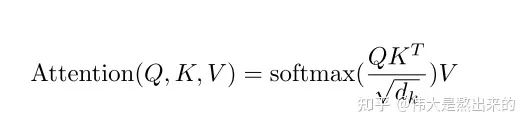
2.?Q?K?V矩陣
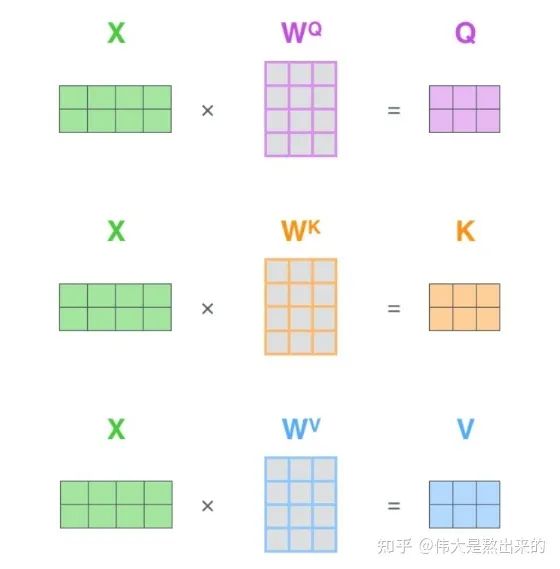
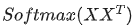 這個(gè)矩陣的意義,相信你也理解了所謂查詢向量一類字眼的含義。
這個(gè)矩陣的意義,相信你也理解了所謂查詢向量一類字眼的含義。3.?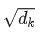 的意義
的意義
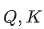 里的元素的均值為0,方差為1,那么?
里的元素的均值為0,方差為1,那么?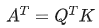 中元素的均值為0,方差為d. 當(dāng)d變得很大時(shí),A中的元素的方差也會(huì)變得很大,如果 A中的元素方差很大,那么
中元素的均值為0,方差為d. 當(dāng)d變得很大時(shí),A中的元素的方差也會(huì)變得很大,如果 A中的元素方差很大,那么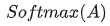 的分布會(huì)趨于陡峭(分布的方差大,分布集中在絕對(duì)值大的區(qū)域)。總結(jié)一下就是
的分布會(huì)趨于陡峭(分布的方差大,分布集中在絕對(duì)值大的區(qū)域)。總結(jié)一下就是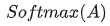 的分布會(huì)和d有關(guān)。因此 A中每一個(gè)元素除以
的分布會(huì)和d有關(guān)。因此 A中每一個(gè)元素除以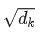 后,方差又變?yōu)?。這使得
后,方差又變?yōu)?。這使得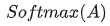 的分布“陡峭”程度與d解耦,從而使得訓(xùn)練過程中梯度值保持穩(wěn)定。
的分布“陡峭”程度與d解耦,從而使得訓(xùn)練過程中梯度值保持穩(wěn)定。# Muti-head Attention 機(jī)制的實(shí)現(xiàn)from math import sqrtimport torchimport torch.nnclass Self_Attention(nn.Module):# input : batch_size * seq_len * input_dim# q : batch_size * input_dim * dim_k# k : batch_size * input_dim * dim_k# v : batch_size * input_dim * dim_vdef __init__(self,input_dim,dim_k,dim_v):super(Self_Attention,self).__init__()self.q = nn.Linear(input_dim,dim_k)self.k = nn.Linear(input_dim,dim_k)self.v = nn.Linear(input_dim,dim_v)self._norm_fact = 1 / sqrt(dim_k)def forward(self,x):Q = self.q(x) # Q: batch_size * seq_len * dim_kK = self.k(x) # K: batch_size * seq_len * dim_kV = self.v(x) # V: batch_size * seq_len * dim_vatten = nn.Softmax(dim=-1)(torch.bmm(Q,K.permute(0,2,1))) * self._norm_fact # Q * K.T() # batch_size * seq_len * seq_lenoutput = torch.bmm(atten,V) # Q * K.T() * V # batch_size * seq_len * dim_vreturn output
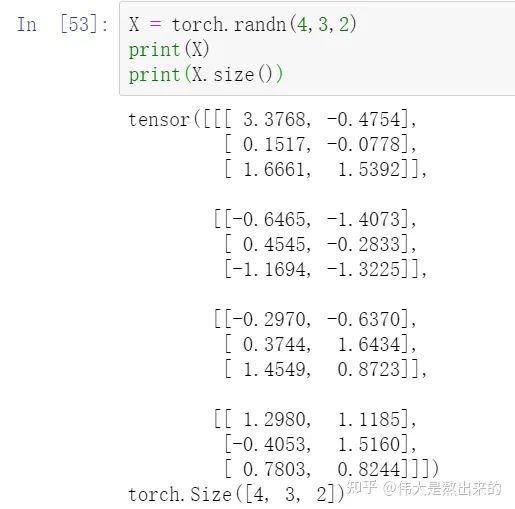

# Muti-head Attention 機(jī)制的實(shí)現(xiàn)from math import sqrtimport torchimport torch.nnclass Self_Attention_Muti_Head(nn.Module):# input : batch_size * seq_len * input_dim# q : batch_size * input_dim * dim_k# k : batch_size * input_dim * dim_k# v : batch_size * input_dim * dim_vdef __init__(self,input_dim,dim_k,dim_v,nums_head):super(Self_Attention_Muti_Head,self).__init__()assert dim_k % nums_head == 0assert dim_v % nums_head == 0self.q = nn.Linear(input_dim,dim_k)self.k = nn.Linear(input_dim,dim_k)self.v = nn.Linear(input_dim,dim_v)self.nums_head = nums_headself.dim_k = dim_kself.dim_v = dim_vself._norm_fact = 1 / sqrt(dim_k)def forward(self,x):Q = self.q(x).reshape(-1,x.shape[0],x.shape[1],self.dim_k // self.nums_head)K = self.k(x).reshape(-1,x.shape[0],x.shape[1],self.dim_k // self.nums_head)V = self.v(x).reshape(-1,x.shape[0],x.shape[1],self.dim_v // self.nums_head)print(x.shape)print(Q.size())atten = nn.Softmax(dim=-1)(torch.matmul(Q,K.permute(0,1,3,2))) # Q * K.T() # batch_size * seq_len * seq_lenoutput = torch.matmul(atten,V).reshape(x.shape[0],x.shape[1],-1) # Q * K.T() * V # batch_size * seq_len * dim_vreturn output
評(píng)論
圖片
表情
