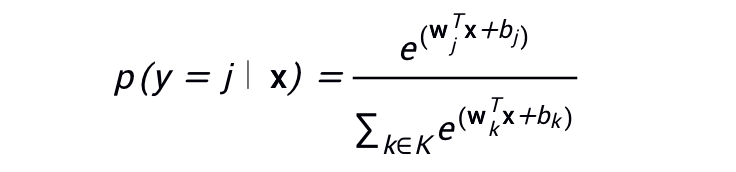神經(jīng)網(wǎng)絡(luò)知識專題總結(jié)!
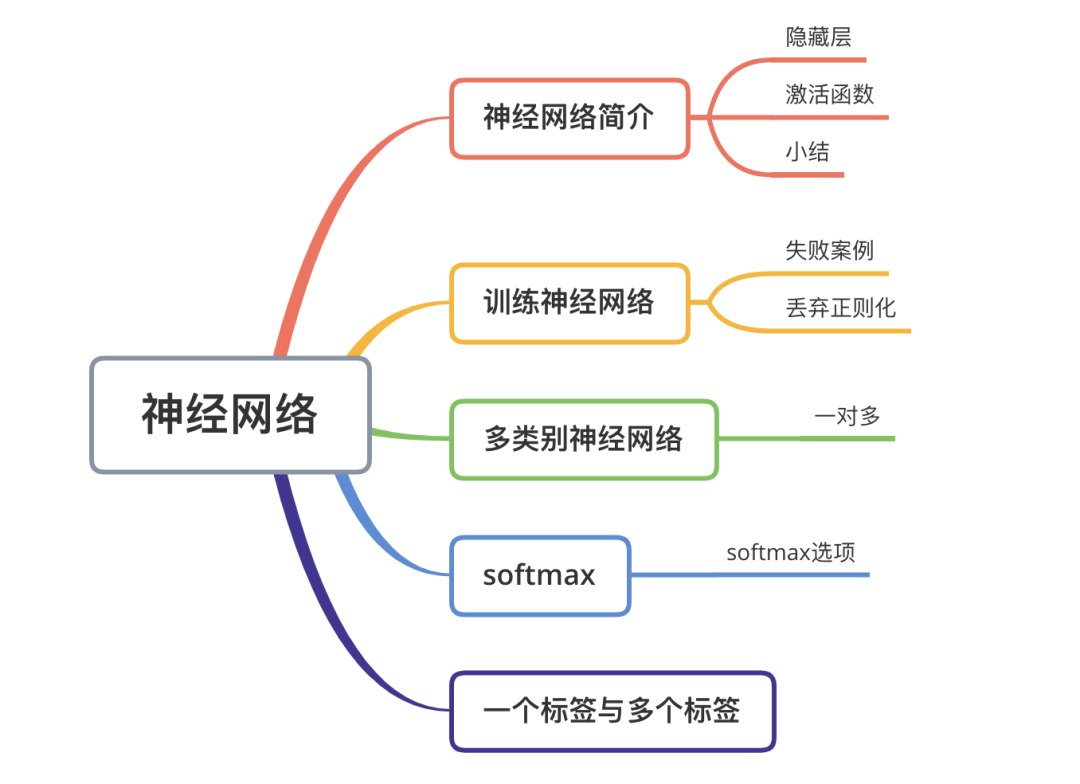
結(jié)構(gòu)總覽
一、神經(jīng)網(wǎng)絡(luò)簡介
對于非線性分類問題(如圖1所示),“非線性”意味著你無法使用形式為:
的模型準(zhǔn)確預(yù)測標(biāo)簽。也就是說,“決策面”不是直線。之前,我們了解了對非線性問題進(jìn)行建模的一種可行方法 - 特征組合。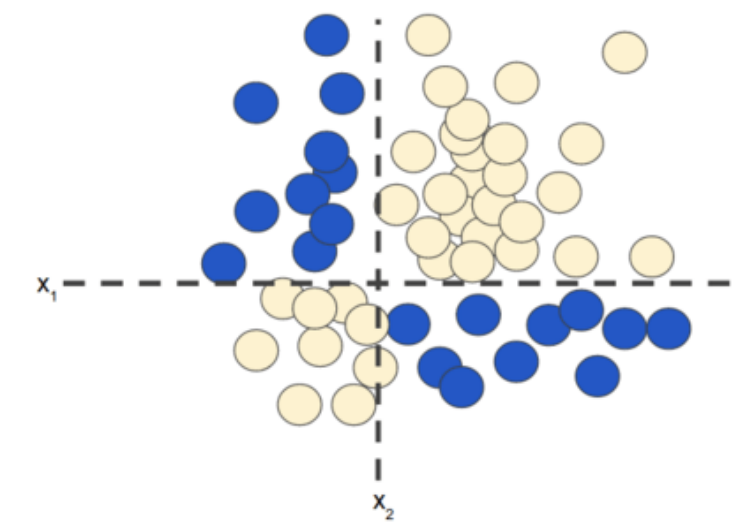
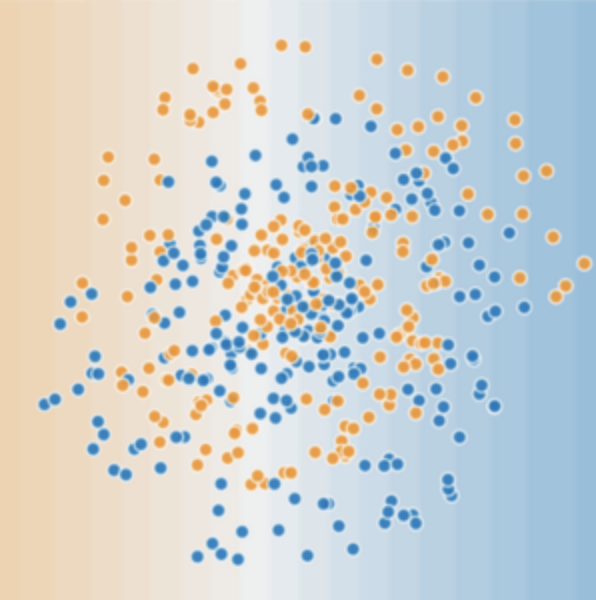
現(xiàn)在,請考慮以下數(shù)據(jù)集:
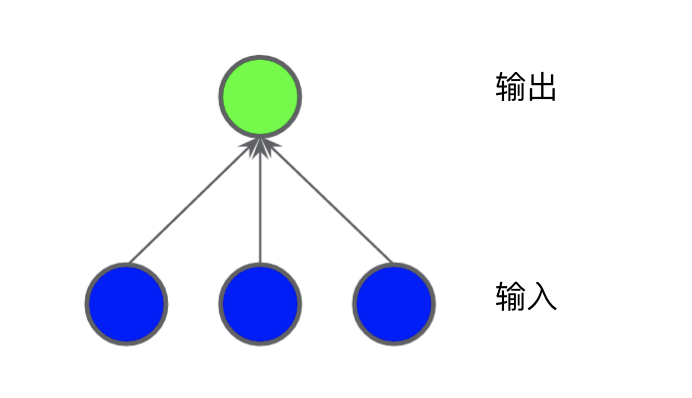
圖 2 所示的數(shù)據(jù)集問題無法用線性模型解決。為了了解神經(jīng)網(wǎng)絡(luò)可以如何幫助解決非線性問題,我們首先用圖表呈現(xiàn)一個線性模型:
每個藍(lán)色圓圈均表示一個輸入特征,綠色圓圈表示各個輸入的加權(quán)和。要提高此模型處理非線性問題的能力,我們可以如何更改它?
1.1 隱藏層
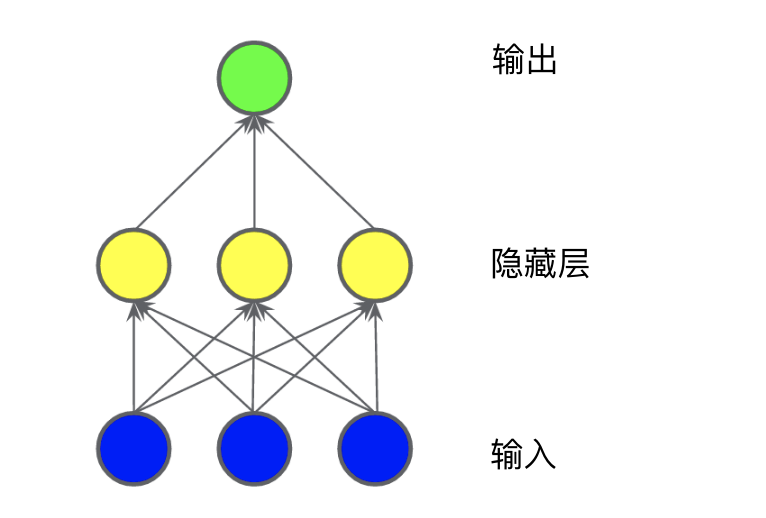
在下圖所示的模型中,我們添加了一個表示中間值的“隱藏層”。隱藏層中的每個黃色節(jié)點均是藍(lán)色輸入節(jié)點值的加權(quán)和。輸出是黃色節(jié)點的加權(quán)和。
此模型是線性的嗎?是的,其輸出仍是其輸入的線性組合。
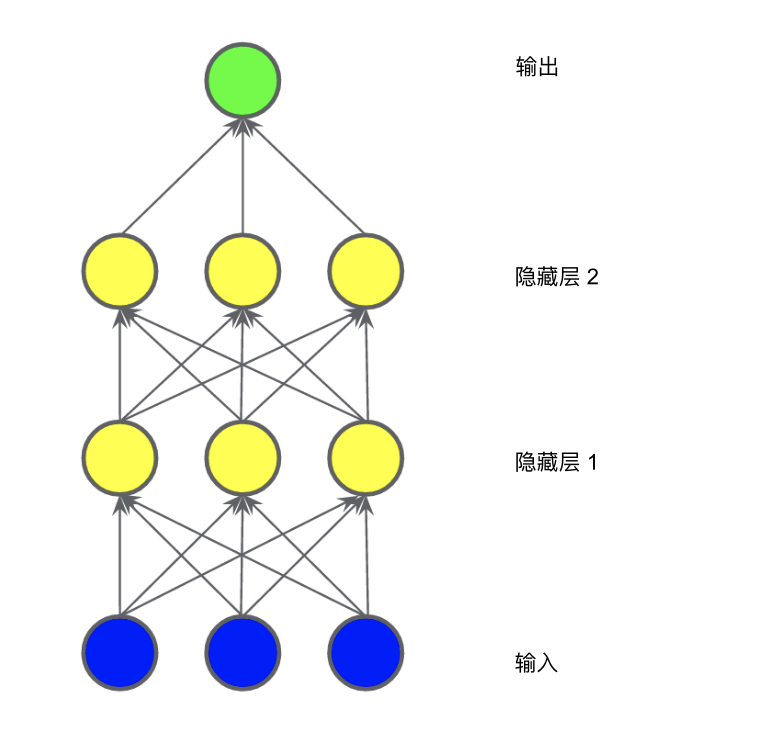
在下圖所示的模型中,我們又添加了一個表示加權(quán)和的“隱藏層”。
此模型仍是線性的嗎?是的,沒錯。當(dāng)你將輸出表示為輸入的函數(shù)并進(jìn)行簡化時,你只是獲得輸入的另一個加權(quán)和而已。該加權(quán)和無法對圖 2 中的非線性問題進(jìn)行有效建模。
1.2 激活函數(shù)
要對非線性問題進(jìn)行建模,我們可以直接引入非線性函數(shù)。我們可以用非線性函數(shù)將每個隱藏層節(jié)點像管道一樣連接起來。
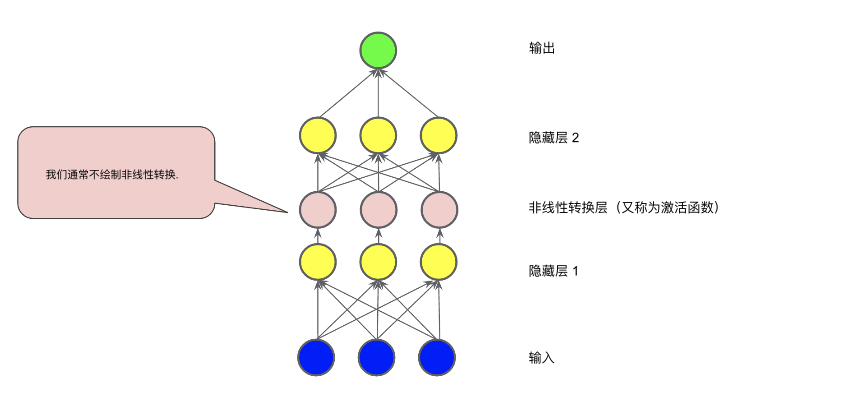
在下圖所示的模型中,在隱藏層 1 中的各個節(jié)點的值傳遞到下一層進(jìn)行加權(quán)求和之前,我們采用一個非線性函數(shù)對其進(jìn)行了轉(zhuǎn)換。這種非線性函數(shù)稱為激活函數(shù)。
現(xiàn)在,我們已經(jīng)添加了激活函數(shù),如果添加層,將會產(chǎn)生更多影響。通過在非線性上堆疊非線性,我們能夠?qū)斎牒皖A(yù)測輸出之間極其復(fù)雜的關(guān)系進(jìn)行建模。簡而言之,每一層均可通過原始輸入有效學(xué)習(xí)更復(fù)雜、更高級別的函數(shù)。如果你想更直觀地了解這一過程的工作原理,請參閱 Chris Olah 的精彩博文。
常見激活函數(shù)
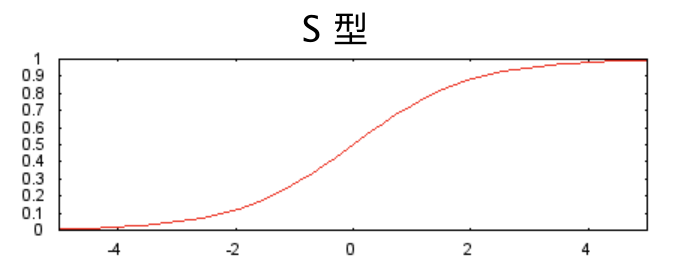
以下 S 型激活函數(shù)將加權(quán)和轉(zhuǎn)換為介于 0 和 1 之間的值。
曲線圖如下:
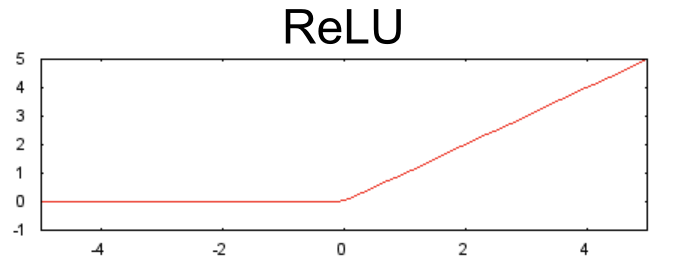
相較于 S 型函數(shù)等平滑函數(shù),以下修正線性單元激活函數(shù)(簡稱為 ReLU)的效果通常要好一點,同時還非常易于計算。
ReLU 的優(yōu)勢在于它基于實證發(fā)現(xiàn)(可能由 ReLU 驅(qū)動),擁有更實用的響應(yīng)范圍。S 型函數(shù)的響應(yīng)性在兩端相對較快地減少。
實際上,所有數(shù)學(xué)函數(shù)均可作為激活函數(shù)。假設(shè) σσ 表示我們的激活函數(shù)(ReLU、S 型函數(shù)等等)。因此,網(wǎng)絡(luò)中節(jié)點的值由以下公式指定:
TensorFlow 為各種激活函數(shù)提供開箱即用型支持。但是,我們?nèi)越ㄗh從 ReLU 著手。
1.3 小結(jié)
現(xiàn)在,我們的模型擁有了人們通常所說的“神經(jīng)網(wǎng)絡(luò)”的所有標(biāo)準(zhǔn)組件:
一組節(jié)點,類似于神經(jīng)元,位于層中。 一組權(quán)重,表示每個神經(jīng)網(wǎng)絡(luò)層與其下方的層之間的關(guān)系。下方的層可能是另一個神經(jīng)網(wǎng)絡(luò)層,也可能是其他類型的層。 一組偏差,每個節(jié)點一個偏差。 一個激活函數(shù),對層中每個節(jié)點的輸出進(jìn)行轉(zhuǎn)換。不同的層可能擁有不同的激活函數(shù)。
警告:神經(jīng)網(wǎng)絡(luò)不一定始終比特征組合好,但它確實可以提供適用于很多情形的靈活替代方案。
二、訓(xùn)練神經(jīng)網(wǎng)絡(luò)
本部分介紹了反向傳播算法的失敗案例,以及正則化神經(jīng)網(wǎng)絡(luò)的常見方法。
2.1 失敗案例
很多常見情況都會導(dǎo)致反向傳播算法出錯。
梯度消失
較低層(更接近輸入)的梯度可能會變得非常小。在深度網(wǎng)絡(luò)中,計算這些梯度時,可能涉及許多小項的乘積。
當(dāng)較低層的梯度逐漸消失到 0 時,這些層的訓(xùn)練速度會非常緩慢,甚至不再訓(xùn)練。
ReLU 激活函數(shù)有助于防止梯度消失。
梯度爆炸
如果網(wǎng)絡(luò)中的權(quán)重過大,則較低層的梯度會涉及許多大項的乘積。在這種情況下,梯度就會爆炸:梯度過大導(dǎo)致難以收斂。批標(biāo)準(zhǔn)化可以降低學(xué)習(xí)速率,因而有助于防止梯度爆炸。
ReLU 單元消失
一旦 ReLU 單元的加權(quán)和低于 0,ReLU 單元就可能會停滯。它會輸出對網(wǎng)絡(luò)輸出沒有任何貢獻(xiàn)的 0 激活,而梯度在反向傳播算法期間將無法再從中流過。由于梯度的來源被切斷,ReLU 的輸入可能無法作出足夠的改變來使加權(quán)和恢復(fù)到 0 以上。
降低學(xué)習(xí)速率有助于防止 ReLU 單元消失。
2.2 丟棄正則化
這是稱為丟棄的另一種形式的正則化,可用于神經(jīng)網(wǎng)絡(luò)。其工作原理是,在梯度下降法的每一步中隨機(jī)丟棄一些網(wǎng)絡(luò)單元。丟棄得越多,正則化效果就越強(qiáng):
0.0 = 無丟棄正則化。 1.0 = 丟棄所有內(nèi)容。模型學(xué)不到任何規(guī)律。
0.0 和 1.0 之間的值更有用。
三、多類別神經(jīng)網(wǎng)絡(luò)
3.1 一對多(OnevsAll)
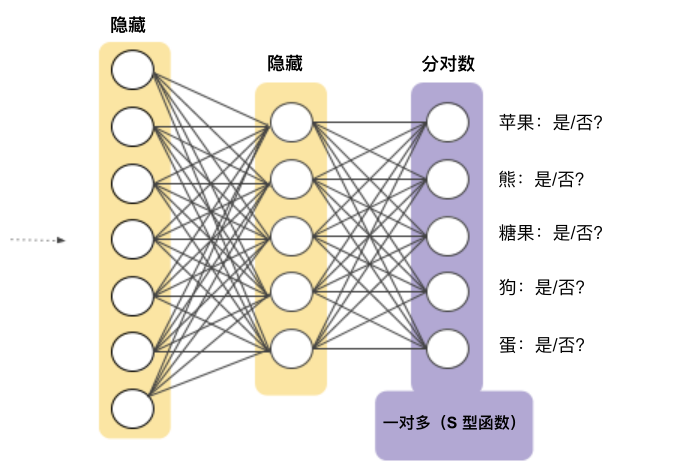
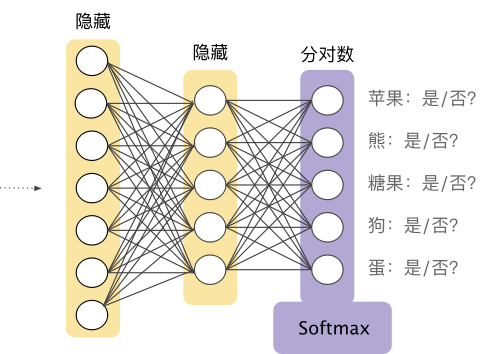
一對多提供了一種利用二元分類的方法。鑒于一個分類問題會有 N 個可行的解決方案,一對多解決方案包括 N 個單獨的二元分類器,每個可能的結(jié)果對應(yīng)一個二元分類器。在訓(xùn)練期間,模型會訓(xùn)練一系列二元分類器,使每個分類器都能回答單獨的分類問題。以一張狗狗的照片為例,可能需要訓(xùn)練五個不同的識別器,其中四個將圖片看作負(fù)樣本(不是狗狗),一個將圖片看作正樣本(是狗狗)。即:
這是一張?zhí)O果的圖片嗎?不是。 這是一張熊的圖片嗎?不是。 這是一張?zhí)枪膱D片嗎?不是。 這是一張狗狗的圖片嗎?是。 這是一張雞蛋的圖片嗎?不是。
當(dāng)類別總數(shù)較少時,這種方法比較合理,但隨著類別數(shù)量的增加,其效率會變得越來越低下。
我們可以借助深度神經(jīng)網(wǎng)絡(luò)(在該網(wǎng)絡(luò)中,每個輸出節(jié)點表示一個不同的類別)創(chuàng)建明顯更加高效的一對多模型。圖9展示了這種方法:
四、Softmax
我們已經(jīng)知道,邏輯回歸可生成介于 0 和 1.0 之間的小數(shù)。例如,某電子郵件分類器的邏輯回歸輸出值為 0.8,表明電子郵件是垃圾郵件的概率為 80%,不是垃圾郵件的概率為 20%。很明顯,一封電子郵件是垃圾郵件或非垃圾郵件的概率之和為 1.0。
Softmax 將這一想法延伸到多類別領(lǐng)域。也就是說,在多類別問題中,Softmax 會為每個類別分配一個用小數(shù)表示的概率。這些用小數(shù)表示的概率相加之和必須是 1.0。與其他方式相比,這種附加限制有助于讓訓(xùn)練過程更快速地收斂。
例如,回到我們在圖 9 中看到的圖片分析示例,Softmax 可能會得出圖片屬于某一特定類別的以下概率:
Softmax 層是緊挨著輸出層之前的神經(jīng)網(wǎng)絡(luò)層。Softmax 層必須和輸出層擁有一樣的節(jié)點數(shù)。
Softmax 方程式如下所示:
請注意,此公式本質(zhì)上是將邏輯回歸公式延伸到了多類別。
4.1 Softmax 選項
請查看以下 Softmax 變體:
完整 Softmax 是我們一直以來討論的 Softmax;也就是說,Softmax 針對每個可能的類別計算概率。 候選采樣指 Softmax 針對所有正類別標(biāo)簽計算概率,但僅針對負(fù)類別標(biāo)簽的隨機(jī)樣本計算概率。例如,如果我們想要確定某個輸入圖片是小獵犬還是尋血獵犬圖片,則不必針對每個非狗狗樣本提供概率。
類別數(shù)量較少時,完整 Softmax 代價很小,但隨著類別數(shù)量的增加,它的代價會變得極其高昂。候選采樣可以提高處理具有大量類別的問題的效率。
五、一個標(biāo)簽與多個標(biāo)簽
Softmax 假設(shè)每個樣本只是一個類別的成員。但是,一些樣本可以同時是多個類別的成員。對于此類示例:
你不能使用 Softmax。 你必須依賴多個邏輯回歸。
例如,假設(shè)你的樣本是只包含一項內(nèi)容(一塊水果)的圖片。Softmax 可以確定該內(nèi)容是梨、橙子、蘋果等的概率。如果你的樣本是包含各種各樣內(nèi)容(幾份不同種類的水果)的圖片,你必須改用多個邏輯回歸。