色婷婷色婷婷,影音先锋色五月,五月天开心激情站,日韩蜜桃久久久,亚洲第一页中文,最新热播日韩女优网站,国产激情自拍视频,国语对白久久

??新智元報(bào)道??

來(lái)源：知乎

編輯：小勻

【新智元導(dǎo)讀】數(shù)學(xué)的重要性不言而喻，那么對(duì)于從事IT行業(yè)的人來(lái)說(shuō)，像高數(shù)、線代這種基礎(chǔ)數(shù)學(xué)課程，應(yīng)該被視為重中之重嗎？

作為一名計(jì)算機(jī)專業(yè)的學(xué)生，你覺(jué)得求學(xué)期間哪門課程最重要？

你又將哪門課程作為學(xué)習(xí)的重中之重呢？

總有人推薦計(jì)算機(jī)學(xué)生把重點(diǎn)放在高數(shù)和線代?

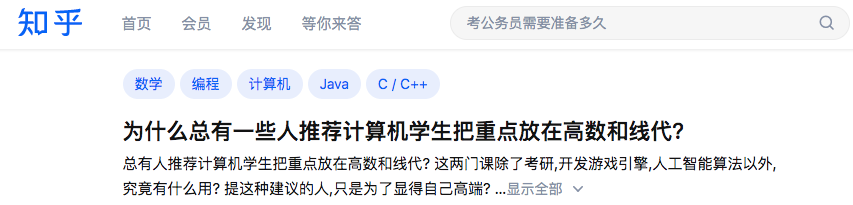
你覺(jué)得呢？

考研黨的心聲：該學(xué)還得學(xué)

眾所周知，計(jì)算機(jī)是一個(gè)非常寬泛的學(xué)科，學(xué)生畢業(yè)后所從事的領(lǐng)域也五花八門，例如有操作系統(tǒng)，編譯，數(shù)據(jù)庫(kù)，逆向工程，信息安全，甚至還有軟件工程等等。

那么，這些領(lǐng)域都需要，或者說(shuō)很需要高數(shù)與線代嗎？

想必本專業(yè)的學(xué)生，此時(shí)腦中蹦出了四個(gè)大字：離、散、數(shù)、學(xué)。

包括非ML的傳統(tǒng)算法在內(nèi)，CS的大部分方向依賴的是數(shù)理邏輯和圖論之類的數(shù)學(xué)分支，具體到大學(xué)本科課程對(duì)應(yīng)的也是離散數(shù)學(xué)，而不是高數(shù)。

但是，作為計(jì)算機(jī)本科生，這是大家放棄高數(shù)和線代的理由嗎？

或許一個(gè)更為龐大的群體：考研黨，會(huì)給出不一樣的答案。

在剛剛過(guò)去的2020年，計(jì)算機(jī)碩士繼續(xù)呈現(xiàn)「爆炸」增長(zhǎng)。以如今計(jì)算機(jī)的缺口，本科畢業(yè)生根本無(wú)法填充，再加上計(jì)算機(jī)的就業(yè)路比較寬，半路出家考研的也大有人在。所以，作為考研必考科目的高數(shù)與線代，當(dāng)然也是非學(xué)不可。

除了應(yīng)試，我們還要關(guān)注作為數(shù)學(xué)基礎(chǔ)，它們有著培養(yǎng)數(shù)學(xué)思維的作用。

數(shù)學(xué)思維對(duì)計(jì)算機(jī)行業(yè)，或者說(shuō)一切理工科都有著無(wú)與倫比的重要性。

如今各種軟件，都與數(shù)學(xué)有必然的聯(lián)系，例如在游戲、圖形軟件開發(fā)中引用了線性代數(shù)中大量的坐標(biāo)變換，矩陣運(yùn)算。而對(duì)開發(fā)游戲引擎，人工智能算法來(lái)說(shuō)，數(shù)學(xué)更是根基，不但開發(fā)引擎需要數(shù)學(xué)知識(shí)，開發(fā)游戲邏輯也需要，所需知識(shí)就基本覆蓋了大學(xué)里《高等數(shù)學(xué)》、《線性代數(shù)》、《概率與數(shù)理統(tǒng)計(jì)》等課程。

崗位上用到高數(shù)多少？

但也有人認(rèn)為，聚焦數(shù)學(xué)固然重要，但不要過(guò)分夸大高數(shù)與線代的重要性。

因?yàn)橄袢斯ぶ悄軑徫弧⒂螒蛞骈_發(fā)崗位等等，還并不能代表程序員群體的全部。

還是回到應(yīng)用更為廣泛的離散數(shù)學(xué)身上，計(jì)算機(jī)本身的存儲(chǔ)結(jié)構(gòu)是離散的。

所以很多時(shí)候，沒(méi)必要過(guò)分強(qiáng)調(diào)「基礎(chǔ)論」，因?yàn)閺挠?jì)算機(jī)系統(tǒng)的角度講，大都依賴的是離散結(jié)構(gòu)的數(shù)學(xué)，而非微分方程。

不是學(xué)習(xí)C/C++方向和考研，沒(méi)有太大的必要把學(xué)習(xí)精力重點(diǎn)放在高數(shù)和線代上面。你更應(yīng)該學(xué)好計(jì)算機(jī)網(wǎng)絡(luò)、操作系統(tǒng)、數(shù)據(jù)庫(kù)、數(shù)據(jù)結(jié)構(gòu)與算法等等計(jì)算機(jī)科學(xué)相關(guān)內(nèi)容，和編程語(yǔ)言以及用編程語(yǔ)言開發(fā)出具體的項(xiàng)目上。

羅杰·培根曾說(shuō)，「數(shù)學(xué)是科學(xué)的大門和關(guān)鍵。」

當(dāng)提到數(shù)學(xué)時(shí)，大多數(shù)人通常會(huì)想到需要數(shù)字并且專注于計(jì)算某種值：

算術(shù)
幾何
代數(shù)
結(jié)石
線性代數(shù)
傅立葉變換
常微分方程
偏微分方程等等

但是，要認(rèn)識(shí)到，數(shù)學(xué)涉及的不止是數(shù)字，它還涵蓋了廣泛的主題：

邏輯
演算法
基本定理
數(shù)學(xué)證明和模型
離散數(shù)學(xué)
計(jì)算理論
信息論
組合學(xué)
集合論
圖論
抽象代數(shù)等等

而且很明顯的是，在一個(gè)程序員不了解某些數(shù)學(xué)理論的情況下，他的編程內(nèi)容極有可能受限。

IT部門需要大量程序員來(lái)創(chuàng)建可自動(dòng)化或簡(jiǎn)化業(yè)務(wù)邏輯的應(yīng)用程序。這些是業(yè)務(wù)線應(yīng)用程序，它們?yōu)楣居脩籼峁┝烁行У赝瓿晒ぷ魉璧男畔ⅰ＿@項(xiàng)工作大部分圍繞大型數(shù)據(jù)庫(kù)進(jìn)行，并將數(shù)據(jù)集縮減為用戶所需的相關(guān)信息。

機(jī)器和尖端技術(shù)的軟件工程通常確實(shí)需要高級(jí)數(shù)學(xué)知識(shí)。在過(guò)去的20年中，已發(fā)展并成為主流的所有無(wú)線技術(shù)都嚴(yán)重依賴于信號(hào)處理算法。信號(hào)處理本身可以涵蓋波形合成和分析，壓縮，加密，前向糾錯(cuò)和調(diào)制/解調(diào)。

現(xiàn)在考慮人工智能，計(jì)算機(jī)視覺(jué)，圖像處理，自然語(yǔ)言處理，模擬，機(jī)器人技術(shù)，通用GPU編程，分布式計(jì)算，并且每年都在繼續(xù)增長(zhǎng)。除了機(jī)器人技術(shù)，智能手機(jī)也在某種程度上取決于上述技術(shù)，所有這些技術(shù)都需要具備高級(jí)數(shù)學(xué)知識(shí)才能很好地完成。

大多數(shù)網(wǎng)站不會(huì)收到大量無(wú)法通過(guò)增加硬件解決問(wèn)題的流量。但是，即使如今硬件的商品價(jià)格上漲，更多的硬件也不永遠(yuǎn)是最好的，甚至也不是簡(jiǎn)單的解決方案。

具有強(qiáng)大的批判性思維和推理能力的經(jīng)驗(yàn)豐富的開發(fā)人員，才是最重要的。例如，對(duì)于像Facebook這樣的公司來(lái)說(shuō)，隨著全球不斷發(fā)生的數(shù)億次互動(dòng)，就更需要高度專業(yè)化的算法來(lái)盡可能高效地運(yùn)營(yíng)網(wǎng)站。

最后引用一句知乎網(wǎng)友的話，讓我們回到現(xiàn)實(shí)：

參考知乎網(wǎng)友回答：

https://www.zhihu.com/question/403076697?utm_source=wechat_session&utm_medium=social&utm_oi=91028414010295500

8&utm_content=group3_supplementQuestions&utm_campaign=shareopn

知乎熱議：高數(shù)、線代應(yīng)該成為計(jì)算機(jī)專業(yè)學(xué)習(xí)的重心嗎？

??新智元報(bào)道??

【新智元導(dǎo)讀】數(shù)學(xué)的重要性不言而喻，那么對(duì)于從事IT行業(yè)的人來(lái)說(shuō)，像高數(shù)、線代這種基礎(chǔ)數(shù)學(xué)課程，應(yīng)該被視為重中之重嗎？