機(jī)器學(xué)習(xí)最強(qiáng)調(diào)參方法!高斯過(guò)程與貝葉斯優(yōu)化
機(jī)器學(xué)習(xí)模型中有大量需要事先進(jìn)行人為設(shè)定的參數(shù),比如說(shuō)神經(jīng)網(wǎng)絡(luò)訓(xùn)練的batch-size,XGBoost等集成學(xué)習(xí)模型的樹(shù)相關(guān)參數(shù),我們將這類(lèi)不是經(jīng)過(guò)模型訓(xùn)練得到的參數(shù)叫做超參數(shù)(Hyperparameter)。人為的對(duì)超參數(shù)調(diào)整的過(guò)程也就是我們熟知的調(diào)參。
機(jī)器學(xué)習(xí)中常用的調(diào)參方法包括網(wǎng)格搜索法(Grid search)和隨機(jī)搜索法(Random search)。
網(wǎng)格搜索是一項(xiàng)常用的超參數(shù)調(diào)優(yōu)方法,常用于優(yōu)化三個(gè)或者更少數(shù)量的超參數(shù),本質(zhì)是一種窮舉法。對(duì)于每個(gè)超參數(shù),使用者選擇一個(gè)較小的有限集去探索。然后,這些超參數(shù)笛卡爾積得到若干組超參數(shù)。網(wǎng)格搜索使用每組超參數(shù)訓(xùn)練模型,挑選驗(yàn)證集誤差最小的超參數(shù)作為最好的超參數(shù)。sklearn中通過(guò)GridSearchCV方法進(jìn)行網(wǎng)格搜索。
隨機(jī)搜索,顧名思義,即在指定的超參數(shù)范圍或者分布上隨機(jī)搜索和尋找最優(yōu)超參數(shù)。相較于網(wǎng)格搜索方法,給定超參數(shù)分布內(nèi)并不是所有的超參數(shù)都會(huì)進(jìn)行嘗試,而是會(huì)從給定分布中抽樣一個(gè)固定數(shù)量的參數(shù),實(shí)際僅對(duì)這些抽樣到的超參數(shù)進(jìn)行實(shí)驗(yàn)。sklearn中通過(guò)RandomizedSearchCV方法進(jìn)行隨機(jī)搜索。
除了上述兩種調(diào)參方法外,本文介紹第三種,也有可能是最好的一種調(diào)參方法,即貝葉斯優(yōu)化(Bayesian optimization)。貝葉斯優(yōu)化是一種基于高斯過(guò)程(Gaussian process)和貝葉斯定理的參數(shù)優(yōu)化方法,近年來(lái)被廣泛用于機(jī)器學(xué)習(xí)模型的超參數(shù)調(diào)優(yōu)。本文不詳細(xì)探討高斯過(guò)程和貝葉斯優(yōu)化的數(shù)學(xué)原理,僅展示高斯過(guò)程和貝葉斯優(yōu)化的基本用法和調(diào)參示例。
在展示貝葉斯優(yōu)化的用法之前,我們先簡(jiǎn)單了解一下高斯過(guò)程。高斯過(guò)程是一種觀測(cè)值出現(xiàn)在一個(gè)連續(xù)域的統(tǒng)計(jì)隨機(jī)過(guò)程,簡(jiǎn)單而言,它是一系列服從正態(tài)分布的隨機(jī)變量的聯(lián)合分布,且該聯(lián)合分布服從于多元高斯分布。
核函數(shù)是高斯過(guò)程的核心概念,決定了一個(gè)高斯過(guò)程的基本性質(zhì)。核函數(shù)在高斯過(guò)程中起生成一個(gè)協(xié)方差矩陣來(lái)衡量任意兩個(gè)點(diǎn)之間的距離,并且可以捕捉不同輸入點(diǎn)之間的關(guān)系,將這種關(guān)系反映到后續(xù)的樣本位置上,用于預(yù)測(cè)后續(xù)未知點(diǎn)的值。常用的核函數(shù)包括高斯核函數(shù)(徑向基核函數(shù))、常數(shù)核函數(shù)、線性核函數(shù)、Matern核函數(shù)和周期核函數(shù)等。
高斯核函數(shù)形式如下:
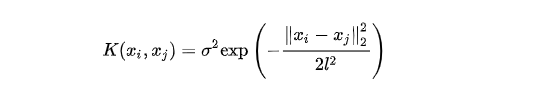
下面我們基于sklearn的高斯過(guò)程接口實(shí)現(xiàn)一個(gè)高斯過(guò)程回歸模型示例。假設(shè)目標(biāo)函數(shù)為:
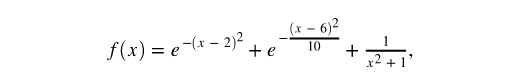
我們通過(guò)一些數(shù)據(jù)點(diǎn)來(lái)基于高斯過(guò)程回歸進(jìn)行擬合。參考代碼如下:
import numpy as npfrom sklearn.gaussian_process import GaussianProcessRegressorfrom sklearn.gaussian_process.kernels import ConstantKernel, RBF# 定義目標(biāo)函數(shù)def target(x):return np.exp(-(x - 2)**2) + np.exp(-(x - 6)**2/10) + 1/ (x**2 + 1)# 訓(xùn)練和測(cè)試數(shù)據(jù)X_train = np.array([-1, 2, 4, 5, 7]).reshape(-1, 1)y_train = target(X_train)X_test = np.linspace(-2, 10, 10000).reshape(-1, 1)# 高斯過(guò)程擬合kernel = ConstantKernel(constant_value=0.2,constant_value_bounds=(1e-4, 1e4)) *RBF(length_scale=0.5, length_scale_bounds=(1e-4, 1e4))gpr = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=2)gpr.fit(X_train, y_train)mu, cov = gpr.predict(X_test, return_cov=True)y_test = mu.ravel()uncertainty = 1.96 * np.sqrt(np.diag(cov))# 繪圖plt.figure()plt.title("l=%.1f sigma_f=%.1f" % (gpr.kernel_.k2.length_scale, gpr.kernel_.k1.constant_value))plt.fill_between(X_test.ravel(), y_test + uncertainty, y_test - uncertainty, alpha=0.1)plt.plot(X_test, y_test, label="predict")plt.scatter(X_train, y_train, label="train", c="red", marker="D")plt.legend()
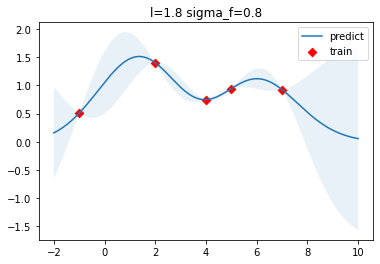
結(jié)果如下圖所示,紅色的方塊點(diǎn)是訓(xùn)練數(shù)據(jù)點(diǎn),藍(lán)色曲線為預(yù)測(cè)的函數(shù)曲線,淺藍(lán)色區(qū)域?yàn)?5%的置信區(qū)間,可以看到在訓(xùn)練數(shù)據(jù)點(diǎn)較為密集的地方,模型預(yù)測(cè)的不確定性較低,而在訓(xùn)練數(shù)據(jù)點(diǎn)比較稀疏的區(qū)域,模型預(yù)測(cè)不確定性較高。真實(shí)的目標(biāo)函數(shù),也就是前面定義的target函數(shù)圖像如下所示:
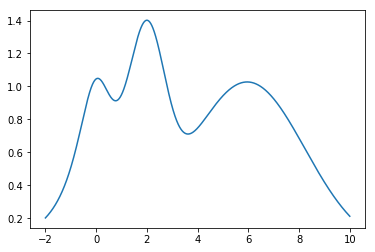
看完了高斯過(guò)程的簡(jiǎn)單示例后,我們?cè)賮?lái)學(xué)習(xí)貝葉斯優(yōu)化。貝葉斯優(yōu)化其實(shí)跟其他優(yōu)化方法一樣,都是為了為了求目標(biāo)函數(shù)取最大值時(shí)的參數(shù)值。作為一個(gè)序列優(yōu)化問(wèn)題,貝葉斯優(yōu)化需要在每一次迭代時(shí)選取一個(gè)最佳觀測(cè)值,這是貝葉斯優(yōu)化的關(guān)鍵問(wèn)題。而這個(gè)關(guān)鍵問(wèn)題正好被上述的高斯過(guò)程完美解決。所以,一般談貝葉斯優(yōu)化必要先了解高斯過(guò)程。
關(guān)于貝葉斯優(yōu)化的大量數(shù)學(xué)原理,包括采集函數(shù)、Upper Confidence Bound (UCB)和EI等概念原理,筆者打算另起一篇文章專(zhuān)門(mén)進(jìn)行闡述。貝葉斯優(yōu)化可直接借用現(xiàn)成的第三方庫(kù)BayesianOptimization來(lái)實(shí)現(xiàn)。直接pip安裝即可:
pip install bayesian-optimization我們同樣是基于前述高斯過(guò)程的目標(biāo)函數(shù),來(lái)看一下貝葉斯優(yōu)化的迭代過(guò)程。代碼示例如下所示。
from bayes_opt import BayesianOptimizationfrom bayes_opt import UtilityFunctionx = np.linspace(-2, 10, 10000).reshape(-1, 1)y = target(x)# 創(chuàng)建貝葉斯優(yōu)化器optimizer = BayesianOptimization(target, {'x': (-2, 10)}, random_state=27)# 隨機(jī)初始化兩個(gè)點(diǎn)optimizer.maximize(init_points=2, n_iter=0, kappa=5)# 定義后驗(yàn)計(jì)算函數(shù)def posterior(optimizer, x_obs, y_obs, grid):optimizer._gp.fit(x_obs, y_obs)mu, sigma = optimizer._gp.predict(grid, return_std=True)return mu, sigma
隨機(jī)初始化的前兩次迭代結(jié)果:
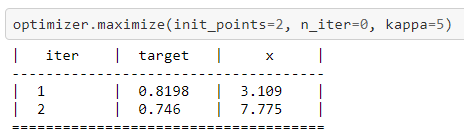
可視化繪圖效果如下:
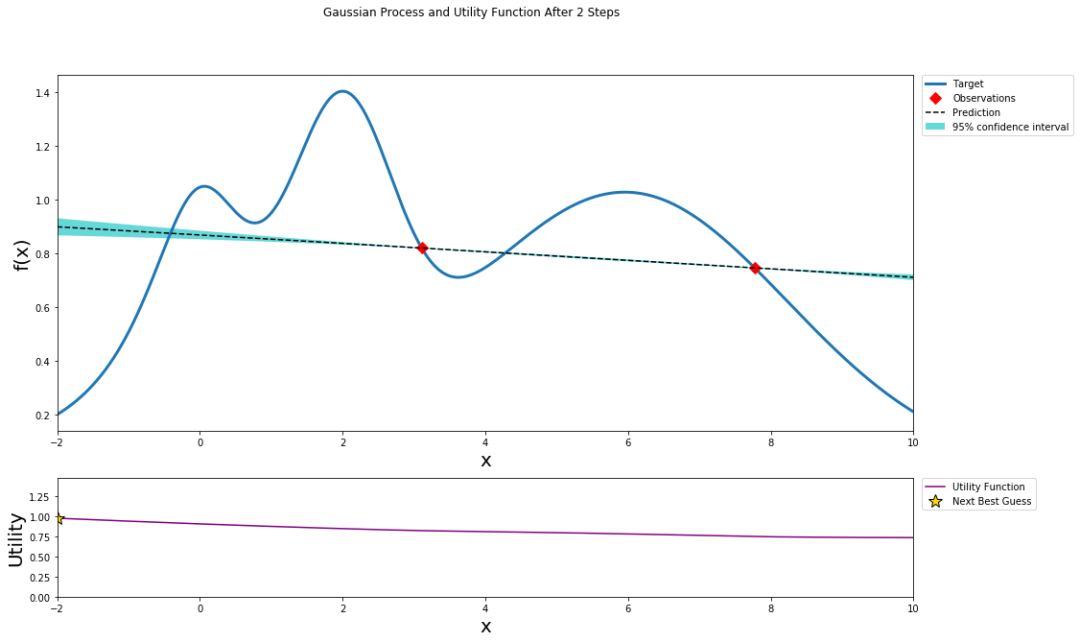
經(jīng)過(guò)9次迭代后,預(yù)測(cè)值逐漸逼近目標(biāo)函數(shù)圖像,結(jié)果如下所示:
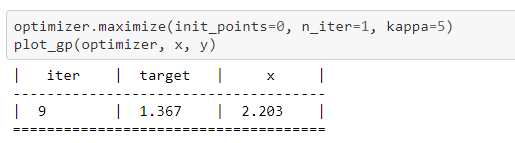
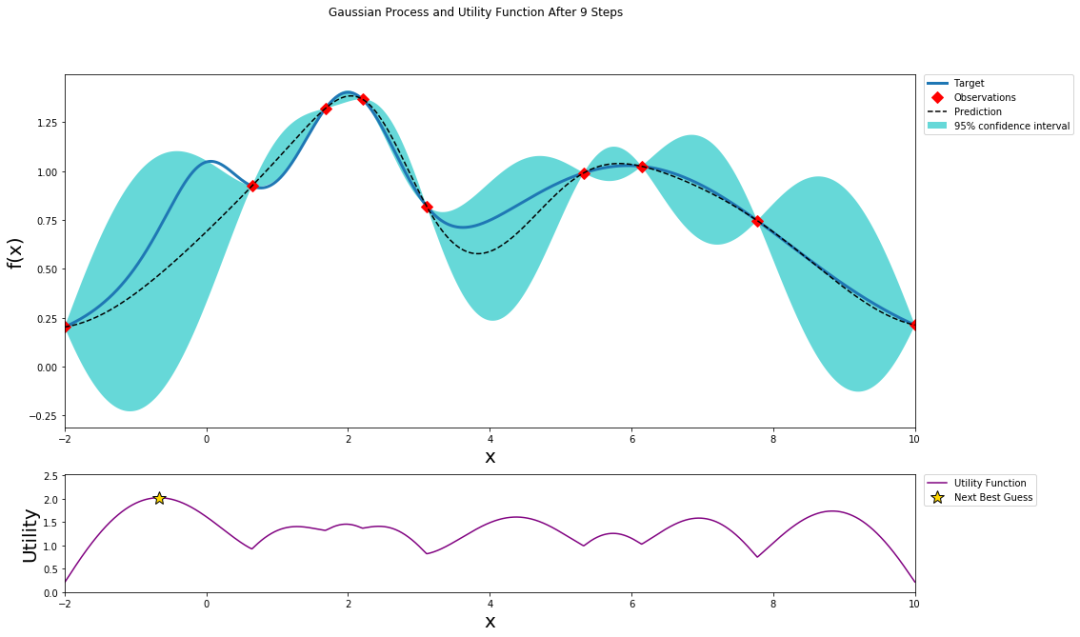
其中虛線為預(yù)測(cè)曲線,藍(lán)色為目標(biāo)函數(shù)曲線,藍(lán)色區(qū)域?yàn)?5%置信區(qū)域。下方紫色曲線為采集函數(shù)。
最后,我們以XGBoost模型為例,給出其基于貝葉斯優(yōu)化的調(diào)參范例。范例數(shù)據(jù)集為kaggle 2015航班延誤數(shù)據(jù)集,目的是預(yù)測(cè)航班是否發(fā)生延誤,是一個(gè)簡(jiǎn)單的二分類(lèi)問(wèn)題。讀取和預(yù)處理過(guò)程如下代碼所示。
import pandas as pdfrom sklearn.model_selection import train_test_splitdata = pd.read_csv("flights.csv")data = data.sample(frac=0.01, random_state=10)data = data[["MONTH","DAY","DAY_OF_WEEK","AIRLINE","FLIGHT_NUMBER","DESTINATION_AIRPORT", "ORIGIN_AIRPORT","AIR_TIME", "DEPARTURE_TIME","DISTANCE","ARRIVAL_DELAY"]]data["ARRIVAL_DELAY"] = (data["ARRIVAL_DELAY"]>10)*1cols = ["AIRLINE","FLIGHT_NUMBER","DESTINATION_AIRPORT","ORIGIN_AIRPORT"]for item in cols:data[item] = data[item].astype("category").cat.codes +1X_train, X_test, y_train, y_test = train_test_split(data.drop(["ARRIVAL_DELAY"],axis=1), data["ARRIVAL_DELAY"], random_state=10, test_size=0.3)print(X_train.shape, y_train.shape, X_test.shape, y_test.shape)

數(shù)據(jù)樣本量為39956*10,測(cè)試為17125*10。
下面以XGBoost模型為例,給出貝葉斯優(yōu)化的調(diào)參過(guò)程。如下代碼所示。
import xgboost as xgbfrom bayes_opt import BayesianOptimizationdef xgb_evaluate(min_child_weight,colsample_bytree,max_depth,subsample,gamma,alpha):params['min_child_weight'] = int(min_child_weight)params['cosample_bytree'] = max(min(colsample_bytree, 1), 0)params['max_depth'] = int(max_depth)params['subsample'] = max(min(subsample, 1), 0)params['gamma'] = max(gamma, 0)params['alpha'] = max(alpha, 0)cv_result = xgb.cv(params, dtrain, num_boost_round=num_rounds, nfold=5,seed=random_state,callbacks=[xgb.callback.early_stop(50)])return cv_result['test-auc-mean'].values[-1]num_rounds = 3000random_state = 2021num_iter = 25init_points = 5params = {'eta': 0.1,'silent': 1,'eval_metric': 'auc','verbose_eval': True,'seed': random_state}xgbBO = BayesianOptimization(xgb_evaluate, {'min_child_weight': (1, 20),'colsample_bytree': (0.1, 1),'max_depth': (5, 15),'subsample': (0.5, 1),'gamma': (0, 10),'alpha': (0, 10),})xgbBO.maximize(init_points=init_points, n_iter=num_iter)
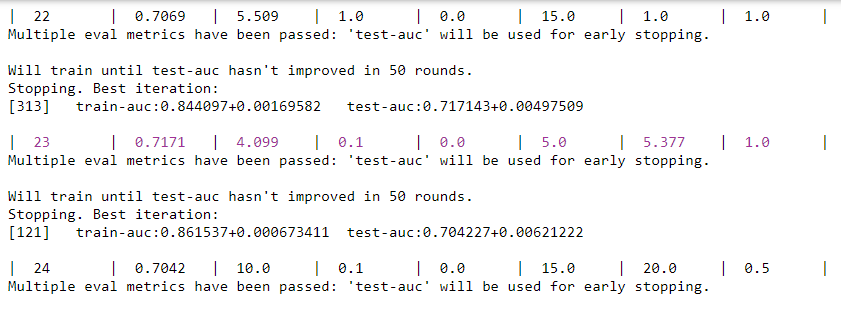
從迭代優(yōu)化結(jié)果可以看到,在第23次迭代時(shí),各超參數(shù)分別為4.099、0.1、、5、5.377和1時(shí),測(cè)試集AUC達(dá)到最優(yōu)的0.7171。
參考資料:
https://github.com/fmfn/BayesianOptimization
Rasmussen C E. Gaussian processes in machine learning[C]//Summer school on machine learning. Springer, Berlin, Heidelberg, 2003: 63-71.
https://scikit-learn.org/stable/modules/gaussian_process.html
往期精彩:
【原創(chuàng)首發(fā)】機(jī)器學(xué)習(xí)公式推導(dǎo)與代碼實(shí)現(xiàn)30講.pdf
【原創(chuàng)首發(fā)】深度學(xué)習(xí)語(yǔ)義分割理論與實(shí)戰(zhàn)指南.pdf
技術(shù)人要學(xué)會(huì)自我營(yíng)銷(xiāo)
點(diǎn)個(gè)在看
