從頻率角度理解為什么深度可以加速神經(jīng)網(wǎng)絡(luò)的訓(xùn)練

深度加速訓(xùn)練的效應(yīng)

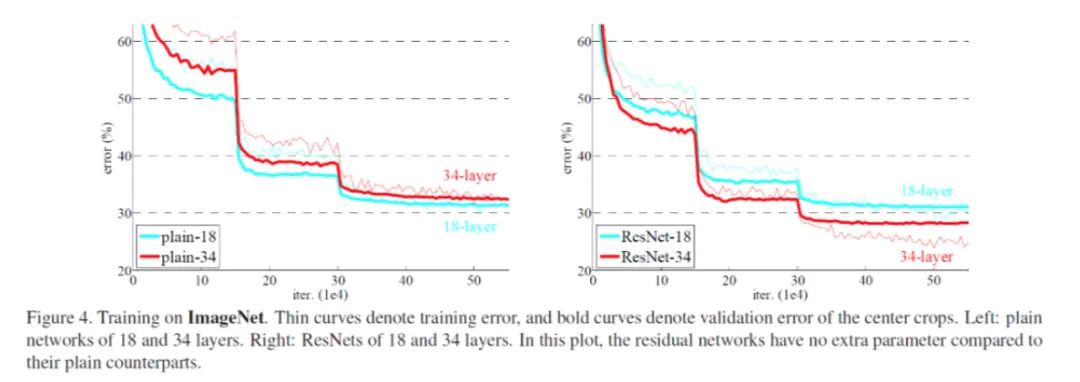
近些年來，隨著深度學(xué)習(xí)的發(fā)展，其已經(jīng)在圖像、語音、自然語言處理等各個(gè)不同的領(lǐng)域展現(xiàn)出了優(yōu)異的性能。在運(yùn)用中，人們發(fā)現(xiàn)，更深層的神經(jīng)網(wǎng)絡(luò)往往比隱藏層較少的神經(jīng)網(wǎng)絡(luò)訓(xùn)練得快，也有更好的泛化性能。雖然，隨著神經(jīng)網(wǎng)絡(luò)的加深，可能會(huì)出現(xiàn)梯度消失的問題，但是通過例如 Resnet 殘差的手段，不僅能解決梯度消失的問題，還能夠提升網(wǎng)絡(luò)的訓(xùn)練速度與泛化性能。

比如何愷明在《Deep Residual Learning for Image Recognition》的實(shí)驗(yàn)，由于加入了殘差塊，34 層的卷積神經(jīng)網(wǎng)絡(luò)的泛化性和訓(xùn)練速度都比 18 層的卷積神經(jīng)網(wǎng)絡(luò)要好。

泛化的問題往往還與數(shù)據(jù)集本身有密切的關(guān)系。因此，我們首先關(guān)注為什么加深網(wǎng)絡(luò)可以加快訓(xùn)練。為避免歧義，我們定義訓(xùn)練快慢是通過看網(wǎng)絡(luò)達(dá)到一個(gè)固定誤差所需要的訓(xùn)練步數(shù)。盡管更深的網(wǎng)絡(luò)每步需要的計(jì)算量更大，但這里我們先忽略這個(gè)因素。

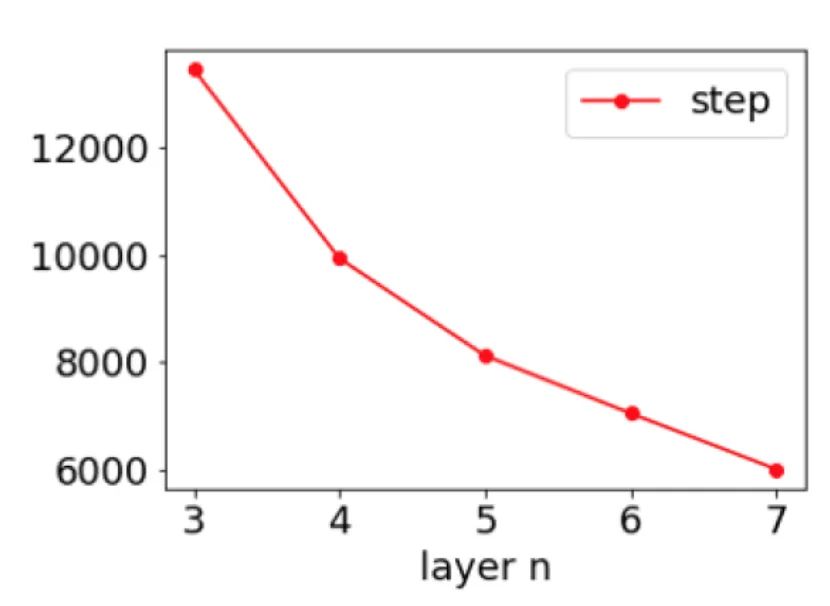
為了研究這個(gè)問題，首先我們用一個(gè)簡單的實(shí)驗(yàn)來重現(xiàn)這個(gè)現(xiàn)象。下圖是用不同層數(shù)但每層大小一致的 DNN 學(xué)習(xí)目標(biāo)函數(shù) cos(3x)+cos(5x)，訓(xùn)練到一個(gè)固定精度所需要的步數(shù)圖。我們發(fā)現(xiàn)，越深層的神經(jīng)網(wǎng)絡(luò)，需要越少的步數(shù)，就能夠完成任務(wù)。

即使是對于這么簡單的任務(wù)，幾乎沒有文章能夠通過數(shù)學(xué)理論來解釋這樣的問題；盡管有一些工作開始分析深度線性網(wǎng)絡(luò)，但仍然幾乎沒有文章能夠從一個(gè)比較清晰的視角，通過實(shí)驗(yàn)或理論，來解釋這樣一個(gè)非線性神經(jīng)網(wǎng)絡(luò)的現(xiàn)象。

因此，即使提供一個(gè)可能的理解視角，也是十分必要的。我們工作提出了一個(gè)深度頻率原則來解釋深度帶來的加速效應(yīng)。在這之前，我們首先來看一下什么叫頻率原則。

頻率原則（Frequency Principle）

頻率原則可以用一句話概括：深度學(xué)習(xí)傾向于優(yōu)先擬合目標(biāo)函數(shù)的低頻部分。

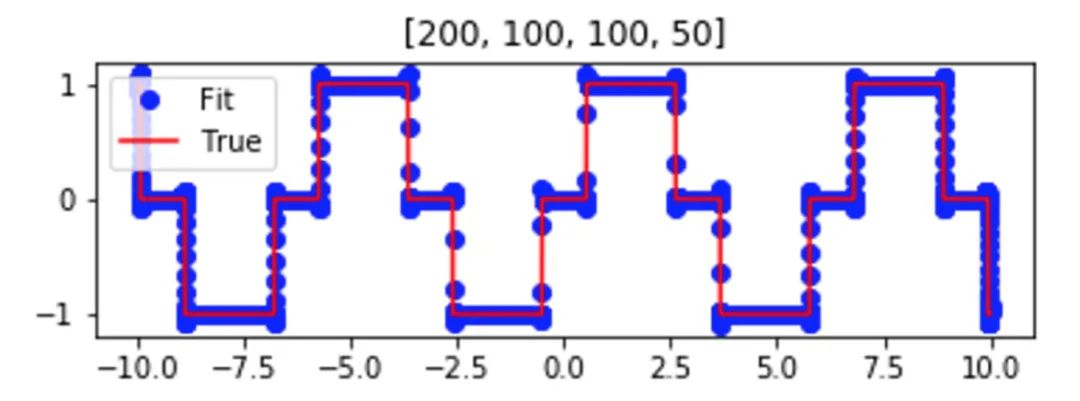
我們先用一個(gè)簡單的例子來理解 F-Principle。用一個(gè)深度神經(jīng)網(wǎng)絡(luò)（DNN）去擬合如下的紅色實(shí)線函數(shù)。訓(xùn)練完成后，函數(shù)能被深度網(wǎng)絡(luò)（藍(lán)色點(diǎn)）很好地?cái)M合。

我們想要從頻域的角度，觀察 DNN 的訓(xùn)練過程。如下圖動(dòng)畫所示，紅色為目標(biāo)函數(shù)的 FT（傅里葉變換），藍(lán)色為網(wǎng)絡(luò)輸出的FT，每一幀表示一個(gè)訓(xùn)練步，橫坐標(biāo)是頻率，縱坐標(biāo)是振幅。我們發(fā)現(xiàn)，隨著訓(xùn)練的進(jìn)行，DNN 表示的函數(shù)在頻域空間顯現(xiàn)出了清晰的規(guī)律，即頻率從低到高依次收斂。

深度頻率原則

接下來，我們將從頻率視角來看深度的影響。對于隱藏層 hi，它的輸入是它前一層的輸出。在神經(jīng)網(wǎng)絡(luò)優(yōu)化過程中，梯度是反向傳播的，也就是說，當(dāng)我們在更新隱藏層 hi 的參數(shù)時(shí)，誤差的信號是從真實(shí)標(biāo)簽和神經(jīng)網(wǎng)絡(luò)輸出的差異開始向前傳播的。

因此，對于子網(wǎng)絡(luò)（從隱藏層 hi 到輸出層），它的等效目標(biāo)函數(shù)是由隱藏層 hi 的前一層的輸出和真實(shí)的標(biāo)簽構(gòu)成。基于此，我們在分析階段將整個(gè)多層的神經(jīng)網(wǎng)絡(luò)分成兩個(gè)部分，pre-condition component 和 learning component，并將著重分析 learning component 的等效目標(biāo)函數(shù)在不同條件下的表現(xiàn)。注意，訓(xùn)練時(shí)，我們?nèi)匀幌裢Ｒ粯樱?xùn)練所有的參數(shù)。

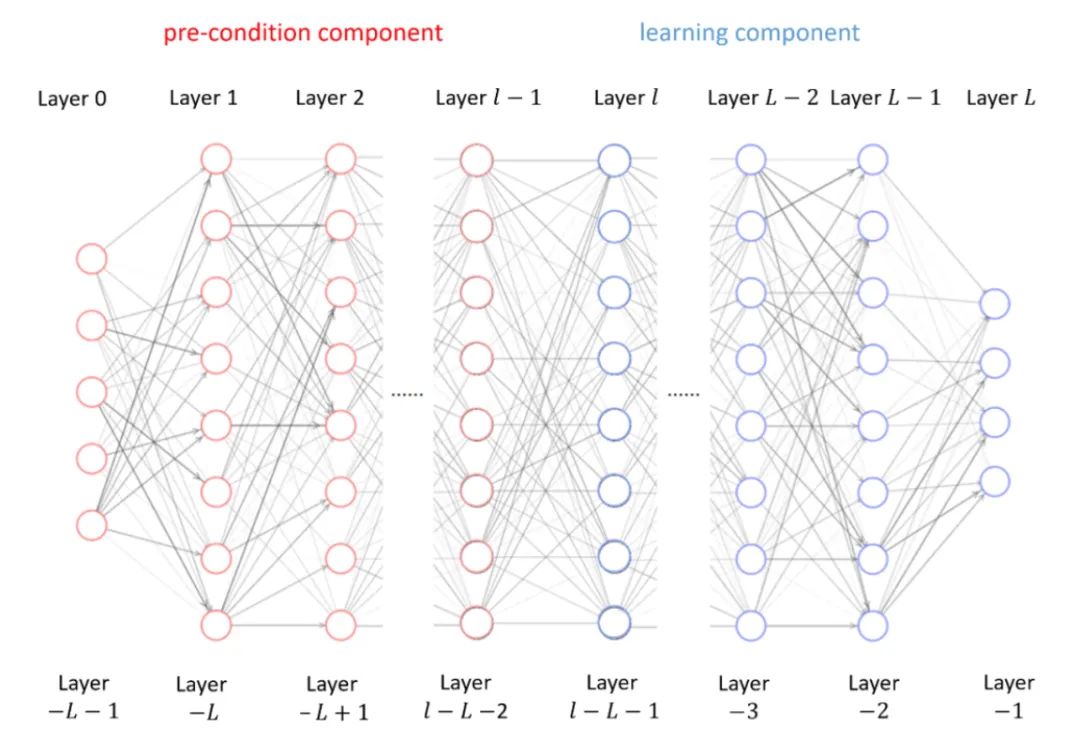
假設(shè)兩個(gè)不同的神經(jīng)網(wǎng)絡(luò)有相同的 learning component，即它們的最后若干層是相同的。若其中一個(gè) learning component 的等效目標(biāo)函數(shù)更加低頻，那這個(gè)神經(jīng)網(wǎng)絡(luò)的 learning component會(huì)學(xué)得更快。

顯然，learning component 學(xué)得更快，自然整個(gè)網(wǎng)絡(luò)也就學(xué)得更快。特別地，當(dāng) learning component 學(xué)好的時(shí)候，整個(gè)神經(jīng)網(wǎng)絡(luò)也就學(xué)好了。因此，這給了我們充分的理由相信，通過研究 learning component 的性質(zhì)，從這個(gè)角度出發(fā)，能夠?qū)Χ鄬由窠?jīng)網(wǎng)絡(luò)的本質(zhì)窺探一二。

現(xiàn)在我們需要做的就是找到一個(gè)可以刻畫高維函數(shù)頻率分布的量，再利用 F-principle 低頻先收斂的特性，我們就可以研究深度帶來的效應(yīng)了。因此，我們定義了 Ratio Density Function (RDF)。

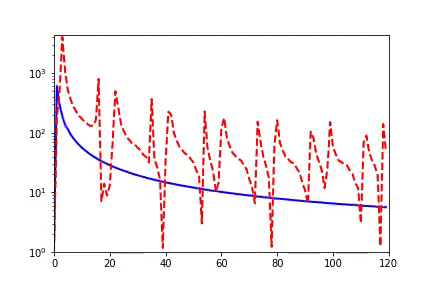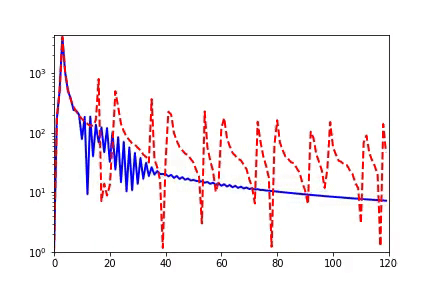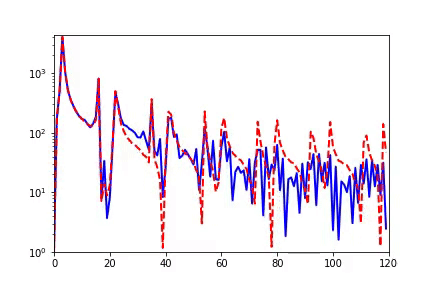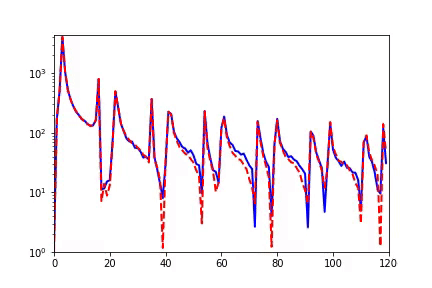
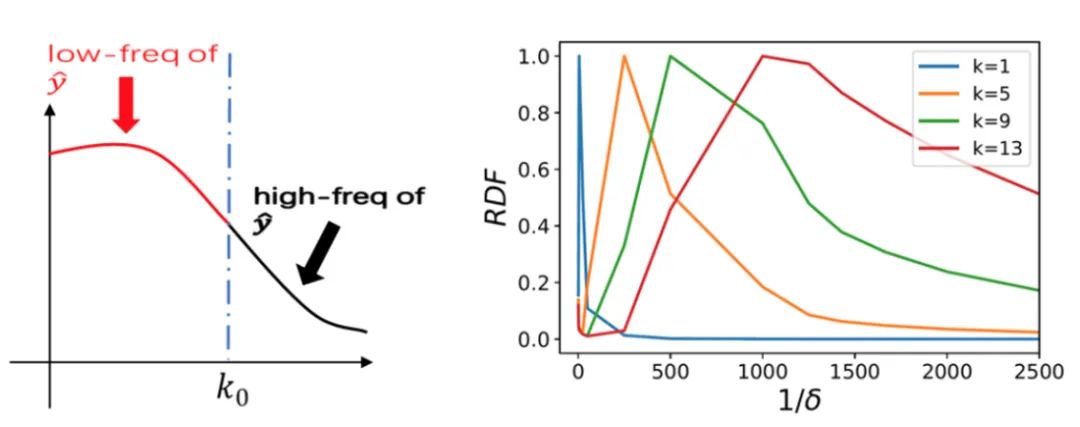
本質(zhì)上，我們首先通過在傅立葉空間畫半徑為 r 的球，定義目標(biāo)函數(shù)在 r 球內(nèi)的能量（L2 積分）占整個(gè)函數(shù)的能量比（通過高斯濾波獲得），即低頻能量比（Low frequency ratio，LFR）。這類似于概率的累積分布函數(shù)。下左圖，就是以 k?為半徑，函數(shù)的 低頻部分與高頻部分。

然后我們對 LFR 在 r 方向上求導(dǎo)數(shù)得到 RDF，這可以解釋為函數(shù)在每個(gè)頻率上的能量密度。下右圖即是，sin（kπx）的 RDF，1/δ 就是半徑 r，并對峰值做了歸一化。不難看出，高頻函數(shù)的峰值在 r 較大的位置，低頻函數(shù)的峰值在 r 較小的位置。因此，RDF 適合用來刻畫高維函數(shù)的頻率分布。

最后，我們需要研究 learning component 的等效目標(biāo)函數(shù)的 RDF。如果 learning component 的等效目標(biāo)函數(shù)的 RDF 趨近于低頻，那么通過 F-principle，我們就知道其收斂得會(huì)比較快；相反，若其趨近于高頻，則其收斂得就會(huì)比較慢。

實(shí)驗(yàn)上，我們先做了關(guān)于 Resnet18 的實(shí)驗(yàn)，保持全連接層不變，改變 Resnet 卷積模塊的個(gè)數(shù)，定義最后三層為 learning component。

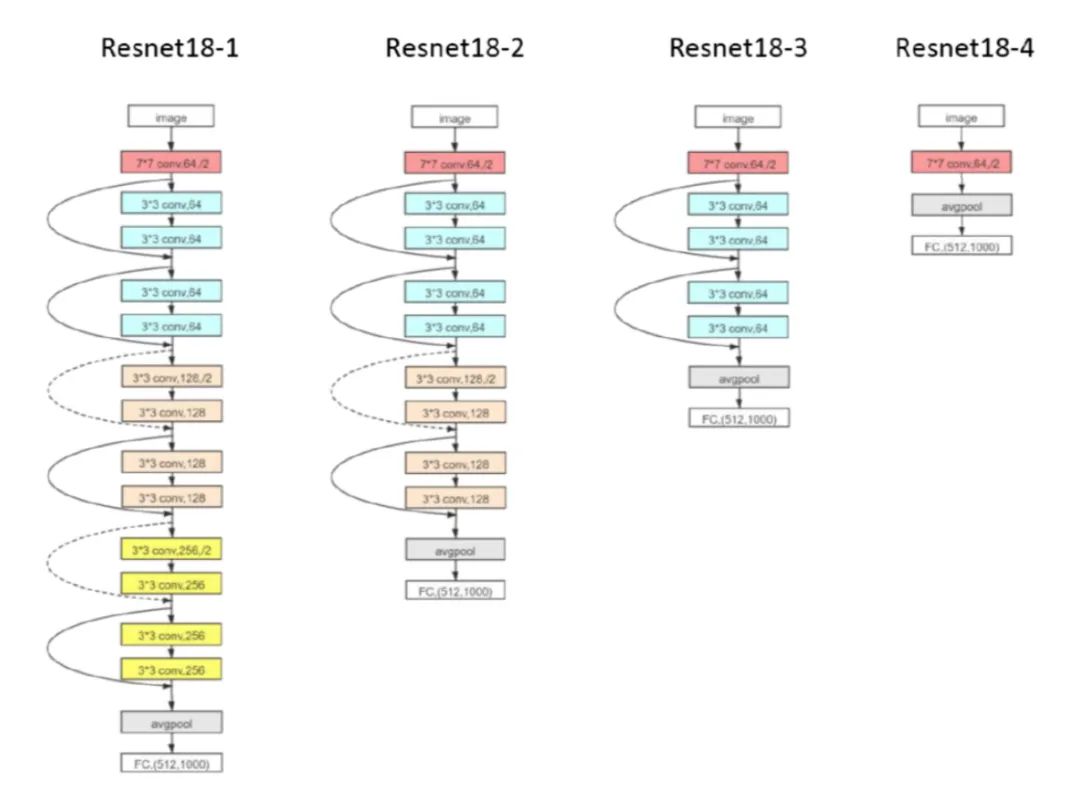
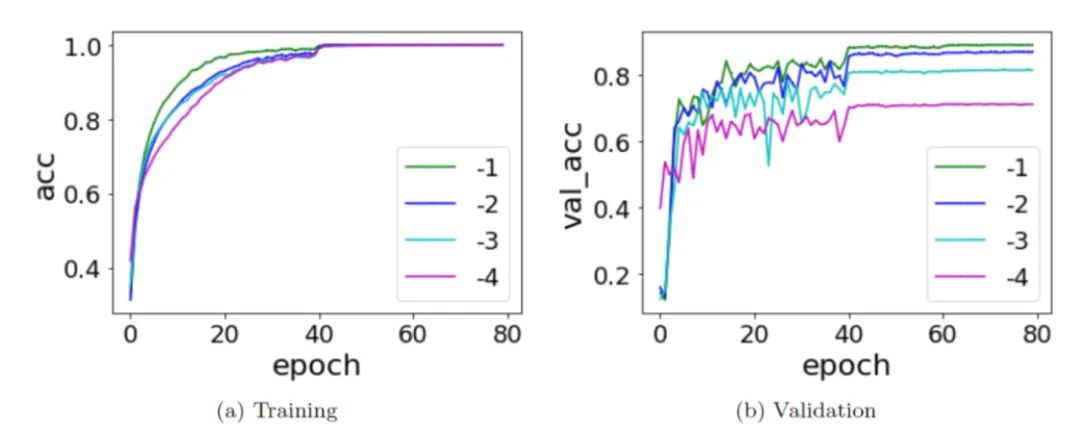
整個(gè)訓(xùn)練和往常一樣，訓(xùn)練所有的參數(shù)。在下圖中，-1、-2、-3、-4 的殘差塊依次減少，不難發(fā)現(xiàn)，擁有更多殘差塊的網(wǎng)絡(luò)不僅收斂速度更快，同時(shí)泛化性能也更好。

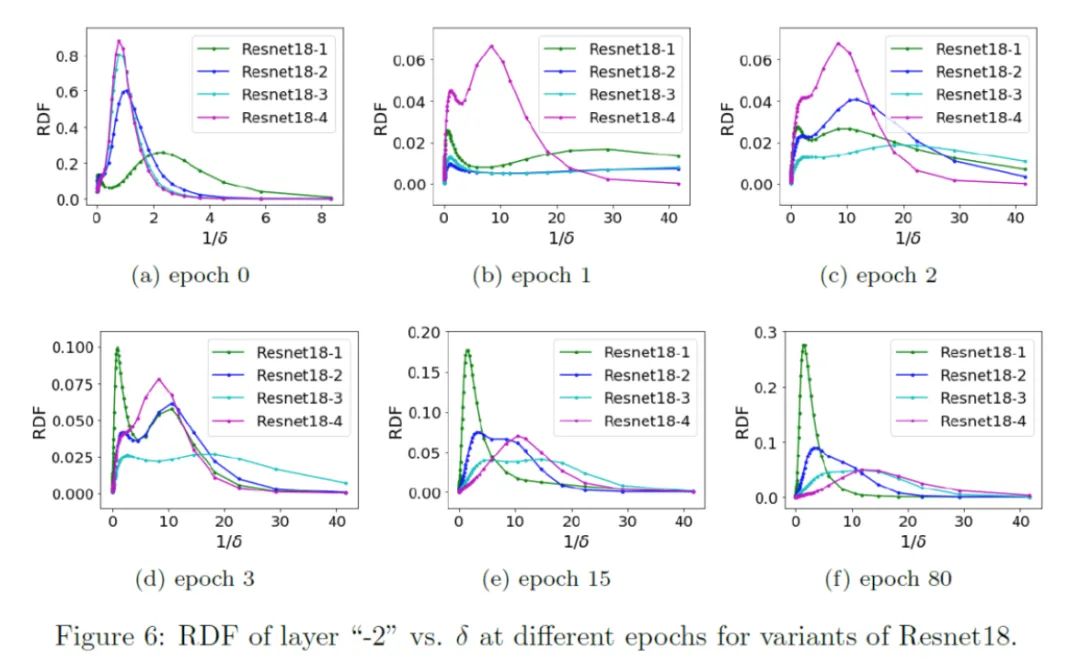
觀察其 learning component 的等效目標(biāo)函數(shù)的 RDF，我們發(fā)現(xiàn)，擁有更多隱藏層（也就是網(wǎng)絡(luò)更深）的神經(jīng)網(wǎng)絡(luò)其 learning component 相比淺網(wǎng)絡(luò)會(huì)更趨于低頻，并最后保持在更加低頻處。我們得到了 Deep Frequency Principle——更深層神經(jīng)網(wǎng)絡(luò)的有效目標(biāo)函數(shù)在訓(xùn)練的過程中會(huì)更趨近于低頻。

再基于 F-principle——低頻先收斂，我們就能夠得到更深層的神經(jīng)網(wǎng)絡(luò)收斂得更快的結(jié)果。盡管頻率是一個(gè)相對可以定量和容易分析的量，但當(dāng)前實(shí)驗(yàn)跨越了多個(gè)不同結(jié)構(gòu)的網(wǎng)絡(luò)，也會(huì)給未來理論分析造成困難。因此，我們后面研究單個(gè)神經(jīng)網(wǎng)絡(luò)中的 Deep Frequency Principle。

于是，我們探究同一個(gè)深度神經(jīng)網(wǎng)絡(luò)內(nèi)不同隱藏層的等效目標(biāo)函數(shù)的 RDF，即改變 pre-condition 和 learning component 的層數(shù)（但保持網(wǎng)絡(luò)的結(jié)構(gòu)和總層數(shù)不變）。這個(gè)實(shí)驗(yàn)是在 MNIST 上的，深度神經(jīng)網(wǎng)絡(luò)（DNN），并取了 5 個(gè)相同大小的隱藏層。

在下圖中，我們發(fā)現(xiàn)，雖然初始時(shí)神經(jīng)網(wǎng)絡(luò)更深層的等效目標(biāo)函數(shù)的 RDF 聚集于較高頻處，但隨著訓(xùn)練，更深層的 RDF 會(huì)快速地趨于更低頻的地方，并保持在低頻處。這也是 Deep Frequency Principle——更深層的神經(jīng)網(wǎng)絡(luò)的有效目標(biāo)函數(shù)會(huì)在訓(xùn)練的過程中會(huì)更趨近于低頻。

在該工作中，基于傅里葉分析以及對 F-principle 的理解，我們給出了一個(gè)新的角度來處理和看待多層、深層的前饋神經(jīng)網(wǎng)絡(luò)，即通過分成 pre-condition component 和 learning component 兩個(gè)部分，研究 learning component 的等效目標(biāo)函數(shù)的 RDF，得到 Deep frequency principle，并最終提供了一種可能的角度來解釋為何多層的網(wǎng)絡(luò)能夠訓(xùn)練得更快！相信這個(gè)工作會(huì)為未來的理論分析提供重要的實(shí)驗(yàn)基礎(chǔ)。

關(guān)于作者：

周瀚旭，許志欽 上海交通大學(xué)

聯(lián)系：[email protected]

https://ins.sjtu.edu.cn/people/xuzhiqin/

參考文獻(xiàn)

[1]?Deep frequency principle towards understanding why deeper learning is faster.? Zhi-Qin John Xu and Hanxu Zhou, arXiv: 2007.14313. (to apear in AAAI-2021)
[2]?Zhi-Qin John Xu; Yaoyu Zhang; Tao Luo; Yanyang Xiao, Zheng Ma , ‘Frequency principle: Fourier analysis sheds light on deep neural networks’, arXiv:1901.06523. (2020, CiCP)[3]?Zhi-Qin John Xu; Yaoyu Zhang; Yanyang Xiao, Training behavior of deep neural network in frequency domain, arXiv preprint arXiv: 1807.01251.?International Conference on Neural Information Processing.