AI | 聊聊決策樹模型
目前決策樹領(lǐng)域,已由原本單一的決策樹模型演變成了級(jí)聯(lián)學(xué)習(xí)樹、隨機(jī)森林模型的天下。
主要使用的就是Boosting和Bagging的思想。
Boosting和Bagging方法本質(zhì)上都是組合學(xué)習(xí),增強(qiáng)了樹模型的準(zhǔn)確率和魯棒性
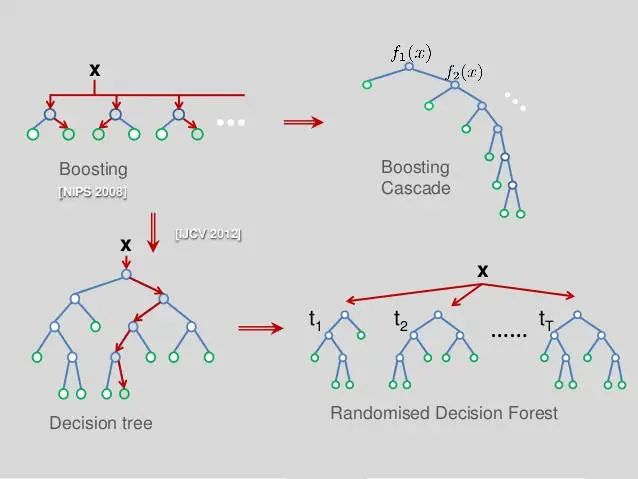
如上圖所示:
Boosting側(cè)重于縱向組合,代表模型為Xgboost
Bagging側(cè)重于橫向組合,代表模型為Random Forest
姑且我們就叫這些樹模型統(tǒng)一為集成決策樹模型吧
但是不管樹模型如何組合,它的本質(zhì)沒有變,最基礎(chǔ)的單元還是cart決策樹
(你也可以說還有C4.5等,不過我覺得這不是重點(diǎn),它們已經(jīng)不是最優(yōu)的基礎(chǔ)單元,該退出歷史舞臺(tái)了)
相比深度學(xué)習(xí)算法
實(shí)現(xiàn)相對簡單,效率更高,訓(xùn)練速度快,訓(xùn)練周期短,能更充分的利用機(jī)器資源
為什么說決策樹模型的效率要高于神經(jīng)網(wǎng)絡(luò)模型?
如上圖所示,就是一個(gè)典型的深度學(xué)習(xí)模型
1.從節(jié)點(diǎn)的計(jì)算量:
神經(jīng)網(wǎng)絡(luò)模型中全連接層節(jié)點(diǎn)的數(shù)量都是預(yù)估的
而決策樹模型的節(jié)點(diǎn)則是根據(jù)信息熵或者基尼系數(shù)生成的,所以在計(jì)算規(guī)模上決策樹模型就會(huì)明顯小于神經(jīng)網(wǎng)絡(luò)模型
2.從訓(xùn)練原理上:
神經(jīng)網(wǎng)絡(luò)模型首先會(huì)將輸入的數(shù)據(jù)進(jìn)行一次激活函數(shù)的洗禮,然后再不斷調(diào)整各節(jié)點(diǎn)的權(quán)重(也即學(xué)習(xí)率),通過多次計(jì)算輸出的殘差得到梯度反過來去影響節(jié)點(diǎn)的權(quán)重,這種節(jié)點(diǎn)整體權(quán)重的變化,相比決策樹模型計(jì)算代價(jià)也高了n個(gè)數(shù)量級(jí)
所以,神經(jīng)網(wǎng)絡(luò)模型所需要的計(jì)算資源相比決策樹來說就非常大了
相比其他傳統(tǒng)機(jī)器學(xué)習(xí)算法
再來看看另一個(gè)引人注目的機(jī)器學(xué)習(xí)算法:支持向量機(jī) SVM
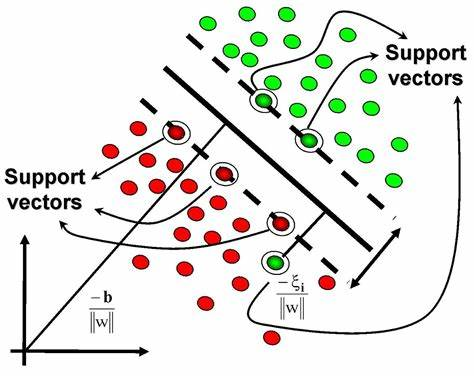
相比SVM,決策樹模型的普適性更強(qiáng),為什么?
因?yàn)镾VM更側(cè)重于對可分割數(shù)據(jù)的分割超平面的尋找和確定,現(xiàn)實(shí)中各種數(shù)據(jù)混雜噪音,是否恰好就有這樣的超平面還兩說,如果沒有這樣的超平面,支持向量點(diǎn)的尋找就變得異常困難,尤其是數(shù)據(jù)量變大的情況下,支持向量機(jī)的計(jì)算大概率會(huì)走向崩潰
小結(jié)
我們不妨做這樣的假設(shè)對比:
如果把所有機(jī)器學(xué)習(xí)模型看作是核機(jī)器
那么集成決策樹模型核函數(shù)可以用數(shù)學(xué)公式簡化為:
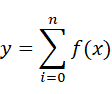
神經(jīng)網(wǎng)絡(luò)模型核函數(shù)可以簡化為:
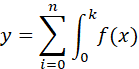
其他傳統(tǒng)機(jī)器學(xué)習(xí)模型的核函數(shù)可以簡化為:
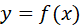
所以,這樣可以一目了然的發(fā)現(xiàn),集成決策樹模型相比神經(jīng)網(wǎng)絡(luò)計(jì)算規(guī)模小,效率高,相比其他傳統(tǒng)機(jī)器學(xué)習(xí)模型,模型復(fù)雜度又恰到好處,模型的表達(dá)能力強(qiáng)于一般模型
聊了這么多決策樹模型的優(yōu)勢,我們再來看看決策樹模型有哪些弊端?
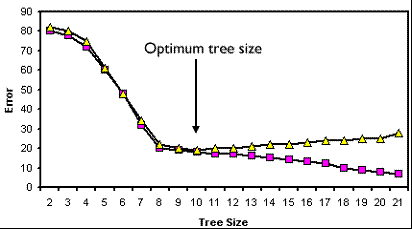
決策樹的規(guī)模預(yù)判
我們在使用XGBoost設(shè)計(jì)和訓(xùn)練一個(gè)集成決策樹模型時(shí),通常會(huì)對下列參數(shù)給出一個(gè)經(jīng)驗(yàn)數(shù)值:
num_parallel_tree
num_boost_round
max_depth
但其實(shí)我們心里也沒譜,不知道以上參數(shù)是否真的恰當(dāng),只能使用GridSearch等參數(shù)搜索工具逐步定位到最優(yōu)參數(shù)范圍
以上參數(shù)代表的含義不難理解:并行樹的數(shù)量、boost次數(shù)、樹最大深度
決策樹的訓(xùn)練過程
我們知道決策樹在進(jìn)行節(jié)點(diǎn)分裂前時(shí),會(huì)遍歷訓(xùn)練集計(jì)算一個(gè)最優(yōu)分裂點(diǎn),這就要求決策樹模型必須遍歷完所有訓(xùn)練集,盡管這個(gè)操作可以不必完全在內(nèi)存中完成(例如XGBoost的大規(guī)模訓(xùn)練解決方案),但是當(dāng)面對日益增長的海量數(shù)據(jù)時(shí),這種必須遍歷完所有數(shù)據(jù)的缺陷也彰顯出來
同時(shí),我們也會(huì)清楚的了解,目前的決策樹的最優(yōu)權(quán)重都是基于目前的訓(xùn)練集的,一旦目標(biāo)數(shù)據(jù)集發(fā)生了變化,這樣的樹模型就不再適用(想想是不是距離智能還很遙遠(yuǎn)?)
決策樹的遷移學(xué)習(xí)
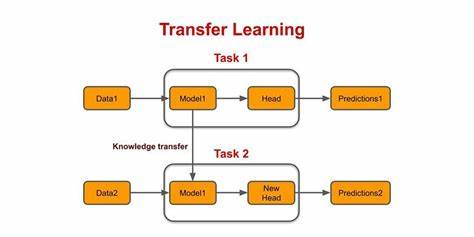
我們知道神經(jīng)網(wǎng)絡(luò)是具備遷移學(xué)習(xí)能力的,而決策樹模型則不具備這些優(yōu)點(diǎn),單獨(dú)將決策樹的某些層拿出來,硬塞到一個(gè)新的數(shù)據(jù)集下,非但起不到加速訓(xùn)練的效果,反而破壞了模型的整體性,導(dǎo)致模型效果變差,所以決策樹模型幾乎無法進(jìn)行遷移,只能集成學(xué)習(xí)
當(dāng)然,對于以上問題,業(yè)界的AI專家們也沒有閑著,想盡一切辦法去讓模型變得更智能和強(qiáng)大
決策樹的規(guī)模預(yù)判問題
首先我們來看第一個(gè)問題,決策樹規(guī)模的預(yù)判
我們在做決策樹模型的設(shè)計(jì)時(shí),往往會(huì)面臨參數(shù)初始化的問題,很多人往往憑經(jīng)驗(yàn)給出一組數(shù)值后,再反復(fù)嘗試對比各參數(shù)從而找到一組合適的數(shù)值。
但該組參數(shù)是否是最優(yōu)的也無從驗(yàn)證,只能是通過對照比較得到效果是已知最好的
目前有兩種策略解決該問題:
1.將決策樹看作組合優(yōu)化問題,使用SAT求解器求解
這里有一篇2020年的代表論文:Efficient Inference of Optimal Decision Trees
論文地址:http://florent.avellaneda.free.fr/dl/AAAI20.pdf
該論文的主要思想在于:分割訓(xùn)練集,并簡化決策樹的分層問題,使得求解的規(guī)模變小,能夠應(yīng)對更大規(guī)模的數(shù)據(jù)集
分而治之的思想在運(yùn)籌問題求解中簡直是萬金油,因此該論文發(fā)表在了AAAI上
筆者也對其作了復(fù)現(xiàn),論文中的開源代碼地址:
https://github.com/FlorentAvellaneda/InferDT
筆者復(fù)現(xiàn)的版本(支持CentOS7):
https://github.com/showkeyjar/InferDT
結(jié)果發(fā)現(xiàn),在處理1-4k個(gè)數(shù)量級(jí)的數(shù)據(jù)樣本時(shí),InferDT還能游刃有余
一旦數(shù)據(jù)量超過了5k,InferDT運(yùn)行的開始變得吃力,最終直接導(dǎo)致崩潰
這也是我們發(fā)現(xiàn)InferDT的示例中并沒有超過1w數(shù)據(jù)量的樣本
所以該論文方法雖然是一種顯著的進(jìn)步,但還不能應(yīng)用到實(shí)際場景中
2.使用分支定界法搜索,然后緩存搜索結(jié)果
同樣有一代表論文:Learning Optimal Decision Trees Using Caching Branch-and-Bound Search
論文地址:
https://dial.uclouvain.be/pr/boreal/fr/object/boreal%3A223390/datastream/PDF_01/view
該論文的主要思想在于:將復(fù)雜難以求解的組合優(yōu)化問題分解為分段(分支定界)的組合優(yōu)化問題,并緩存了計(jì)算結(jié)果,避免重復(fù)的從頭計(jì)算,加快計(jì)算速度
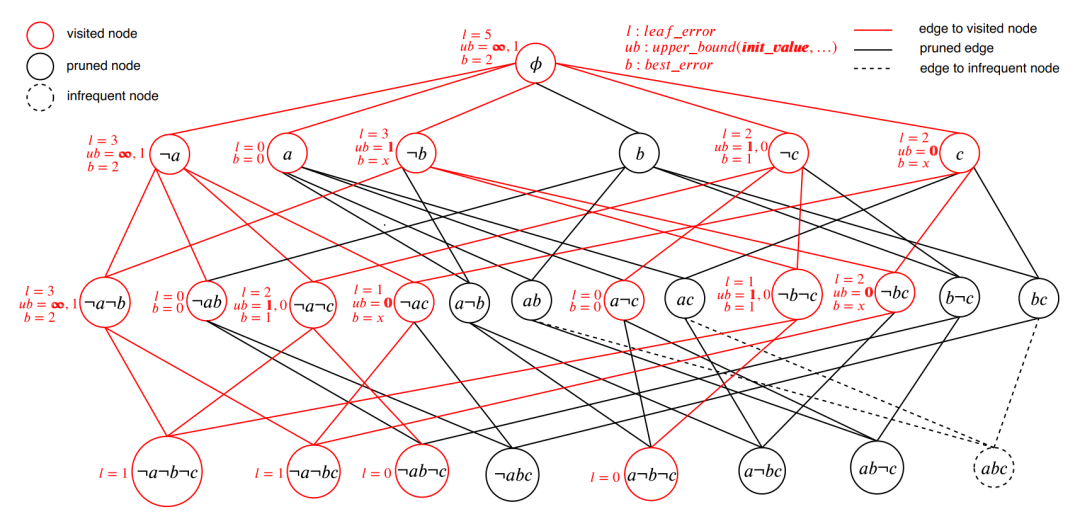
并由此設(shè)計(jì)出DL8.5算法,并兼容了sklearn
本質(zhì)上也是一種分而治之的思想,和方法1有異曲同工之妙
如果大家有興趣,也可以仔細(xì)研究研究這兩篇論文
決策樹的訓(xùn)練問題
目前業(yè)界大神們一直在想辦法克服決策樹訓(xùn)練過程中的一些缺陷
神經(jīng)網(wǎng)絡(luò)的解決方案:
這其中最優(yōu)代表性的作品,就屬2019年誕生的 tabnet :
https://github.com/dreamquark-ai/tabnet
論文地址:https://arxiv.org/pdf/1908.07442v5
tabnet號(hào)稱自己是 xgboost + 神經(jīng)網(wǎng)絡(luò)的組合體,即具備神經(jīng)網(wǎng)絡(luò)反向傳播的特點(diǎn),又具備了集成決策樹的高效和準(zhǔn)確
那么tabnet如何解決決策樹訓(xùn)練時(shí)必須遍歷整個(gè)訓(xùn)練集的問題呢?
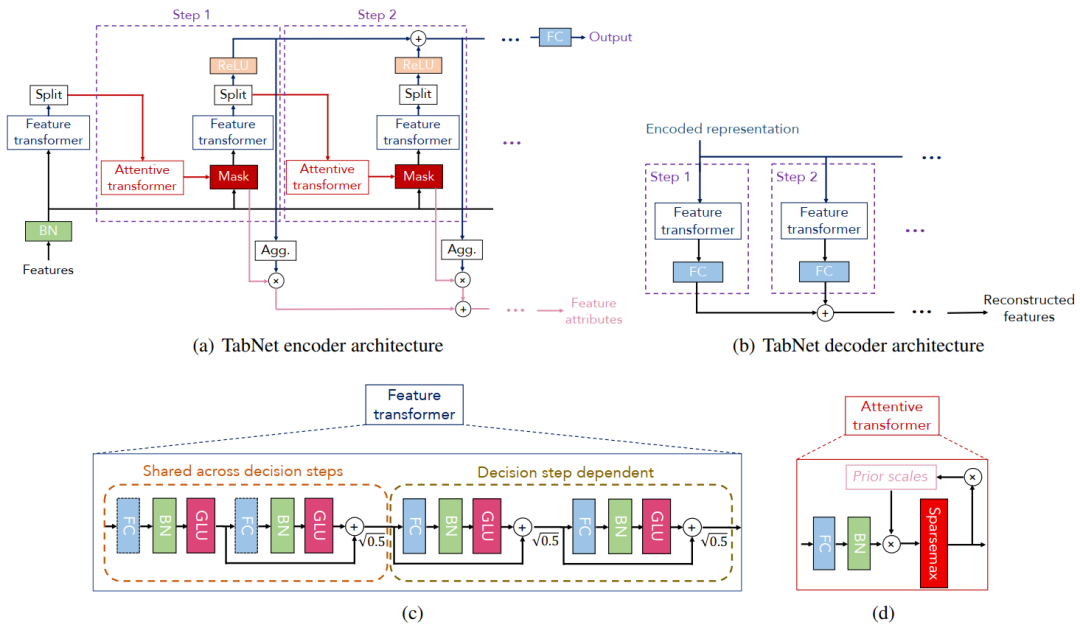
看到上圖中tabnet的網(wǎng)絡(luò)結(jié)構(gòu),是不是感覺和LSTM很類似?
我認(rèn)為實(shí)際上可以把tabnet看作一種LSTM的變體,也使用到了transformer單元,而transformer技術(shù)也是2020年度最熱門的一種深度學(xué)習(xí)技術(shù),本質(zhì)上是對輸入數(shù)據(jù)的“主成分”自動(dòng)分析和提取的過程
所以tabnet試圖通過神經(jīng)網(wǎng)絡(luò)模擬決策樹尋找分裂點(diǎn)的過程,從而讓神經(jīng)網(wǎng)絡(luò)具備較好的可解釋性
另外還有一個(gè)筆者注意到的項(xiàng)目QuantumForest:
https://github.com/closest-git/QuantumForest
論文地址:https://arxiv.org/pdf/2010.02921v1
QuantumForest針對決策樹訓(xùn)練過程中信息熵和基尼系數(shù)的計(jì)算進(jìn)行了改造,改變了一種思維方式,使用神經(jīng)網(wǎng)絡(luò)使得樹模型具有了可微性(differentiability)
筆者理解是決策樹的輸出結(jié)果是離散的,不具備可微性,通過神經(jīng)網(wǎng)絡(luò)將樹模型分裂點(diǎn)的信息熵變更為量子狀態(tài),使得決策樹具備了連續(xù)可微的條件
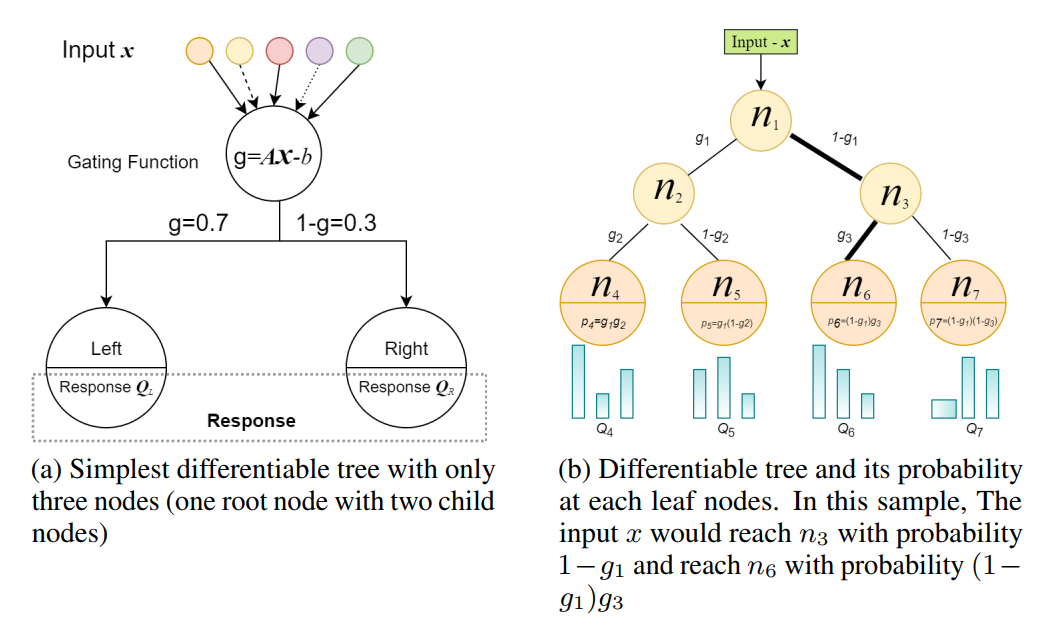
如圖所示,傳統(tǒng)的決策樹模型在分裂節(jié)點(diǎn)時(shí),得到的是一個(gè)確定的信息增益,而在QF里得到則
是一個(gè)浮點(diǎn)數(shù)(量子態(tài)概率)
QF項(xiàng)目的思想還是挺不錯(cuò)的,不過作者好像很懶,開源出來的作品工業(yè)化程度并不高,需要自己去解決易用性問題
決策樹的遷移問題
也有大神在決策樹的遷移領(lǐng)域放大招:
有對應(yīng)的開源項(xiàng)目:https://github.com/atiqm/Transfer_DT
不過竟然沒人關(guān)注,貌似沒搞起來,有興趣的同學(xué)也可以研究下,不妨也給筆者分享一下你的奇思妙想,期待你的創(chuàng)意
總之決策樹模型領(lǐng)域是一個(gè)正在茁壯成長而又活力四射的領(lǐng)域,不斷有人在為其發(fā)展添磚加瓦,而決策樹+集成學(xué)習(xí)+神經(jīng)網(wǎng)絡(luò)正逐漸向我們走來,相信未來的決策樹算法會(huì)更加強(qiáng)大而高效。真正的可解釋性人工智能也會(huì)不斷突破現(xiàn)有的技術(shù)障礙和缺陷,變得更加完美。希望我們能共同挖掘和分享出決策樹的無窮魅力,謝謝閱讀!
---------------------------End---------------------------
10000+人已加入矩陣司南
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
非常感謝對我們的支持! 
