原理+代碼|深入淺出Python隨機森林預(yù)測實戰(zhàn)
本文是Python商業(yè)數(shù)據(jù)挖掘?qū)崙?zhàn)的第3篇
3?- 隨機森林預(yù)測寬帶客戶離網(wǎng)
前言
組合算法也叫集成學(xué)習(xí),在金融行業(yè)或非圖像識別領(lǐng)域,效果有時甚至比深度學(xué)習(xí)還要好。能夠理解基本原理并將代碼用于實際的業(yè)務(wù)案例是本文的目標(biāo),本文將詳細(xì)介紹如何利用Python實現(xiàn)集成學(xué)習(xí)中隨機森林這個經(jīng)典的方法來預(yù)測寬帶客戶的流失,主要將分為兩個部分:
詳細(xì)原理介紹
Python代碼實戰(zhàn)
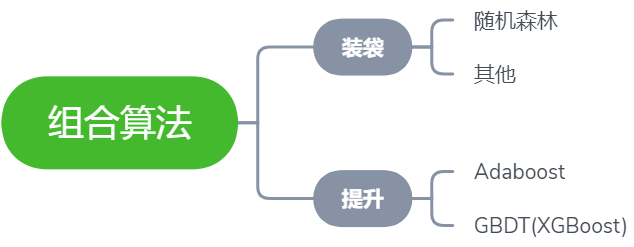
集成學(xué)習(xí)
本文的主角是隨機森林,所以我們將以隨機森林所屬的分支 —— 裝袋法 入手,深入淺出該集成學(xué)習(xí)方法的原理步驟。裝袋法流程如下
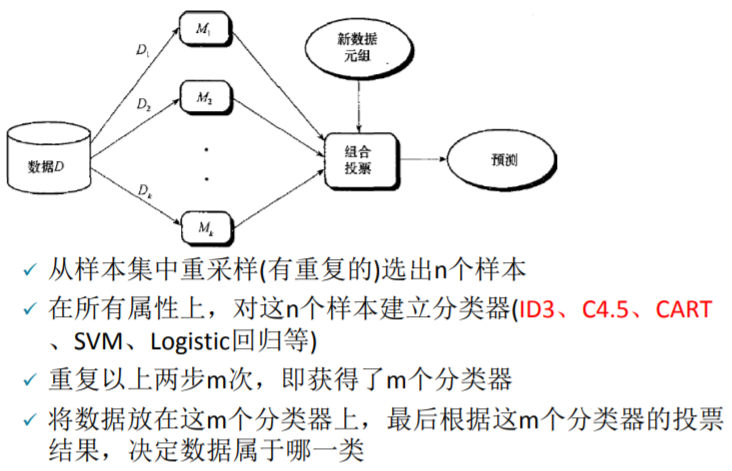
乍一看圖中的步驟可能有些復(fù)雜,現(xiàn)在來逐步拆解。裝袋法中的裝袋二字是精髓,顧名思義即將多個模型裝入同一個袋子后,讓這個袋子作為一個新的模型來實現(xiàn)預(yù)測需求,僅此而已。換句話說,即把多個模型組合起來形成一個新的大模型,這個大模型最終給出的預(yù)測結(jié)果是由這多個小模型綜合決定的,決定方式為少數(shù)服從多數(shù)。

假設(shè)有10萬條原始數(shù)據(jù),用這些數(shù)據(jù)來做十棵決策樹(當(dāng)然也可以是其他模型),最后這10棵樹將被裝進(jìn)了同一個袋子中。這時候取其中一條數(shù)據(jù)放入這個袋子,便會得出10個預(yù)測值(每棵樹各一個),假如其中三棵樹給出的預(yù)測值為0,剩余的七棵給出的為1,那我們便可知道這個袋子對這個數(shù)據(jù)的預(yù)測結(jié)果為 0 的概率是 3/10。

為了更深入的理解裝袋法,下面將回答三個與裝袋法有關(guān)的常見問題:
問:袋子中的每個模型使用的樣本量范圍應(yīng)為多少合適?
答:如果是上面的例子,袋子里面有十棵樹,源數(shù)據(jù)總量為 10萬 條,則每棵樹取用的樣本量的最小值為最少是1w個(10w/10棵 = 1w/棵),因為至少要保證不能浪費樣本,但每棵樹最多可取用多少樣本呢?其實在樣本量已知,同一袋子中模型個數(shù)為n的情況下,樣本的選擇比例為1/n ~ 0.8最好。每個小模型取用 100% 的樣本是絕對沒有意義的,那就跟沒抽是一樣的,這樣也就沒有體現(xiàn)出裝袋,只有每個模型用到的數(shù)據(jù)都有一定的不同,組合起來后每個的投票(預(yù)測結(jié)果)也才有意義。

問:袋中模型們之間的相關(guān)性會影響最后的決策結(jié)果嗎?
答:裝袋法思路最重要的一點:袋子中每個模型之間不能相關(guān),越不相關(guān)越好,這里的不相關(guān)主要體現(xiàn)在用于訓(xùn)練每個模型的樣本不一樣。其次,每個模型的精度越高越好,這樣它的投票才更有價值。
PS:訓(xùn)練模型的樣本不一樣這一點可以理解為總統(tǒng)選舉,抽 10 波選民來投票,這 10 波選民的差異性越大越好,這樣一來,只有在選民千差萬別的情況下你依然脫穎而出,才足以說明你的實力,如果這10波選民中每一波之間的差異性都很小,比如都是本來就偏袒于總統(tǒng)候選人,那投票結(jié)果的說服力就會大減。

問:上面所說的模型精度高是不是哪怕模型很復(fù)雜也可以,如果每個模型的精度高但都過度擬合怎么辦?
答:在裝袋法中,模型是越精確越好,哪怕是過度擬合的也沒有關(guān)系。因為一個模型要想在訓(xùn)練集上做到越精確越好,而精確程度與模型的復(fù)雜度大多是成正比的,所以出現(xiàn)過擬合的情況也是正常且情有可原的。復(fù)雜和過度擬合只是對袋子中每個模型而言,因為最后都會被加權(quán),所以整個袋子(整體)并不會出現(xiàn)過度擬合的情況。
隨機森林
隨機森林的實現(xiàn)步驟如下:
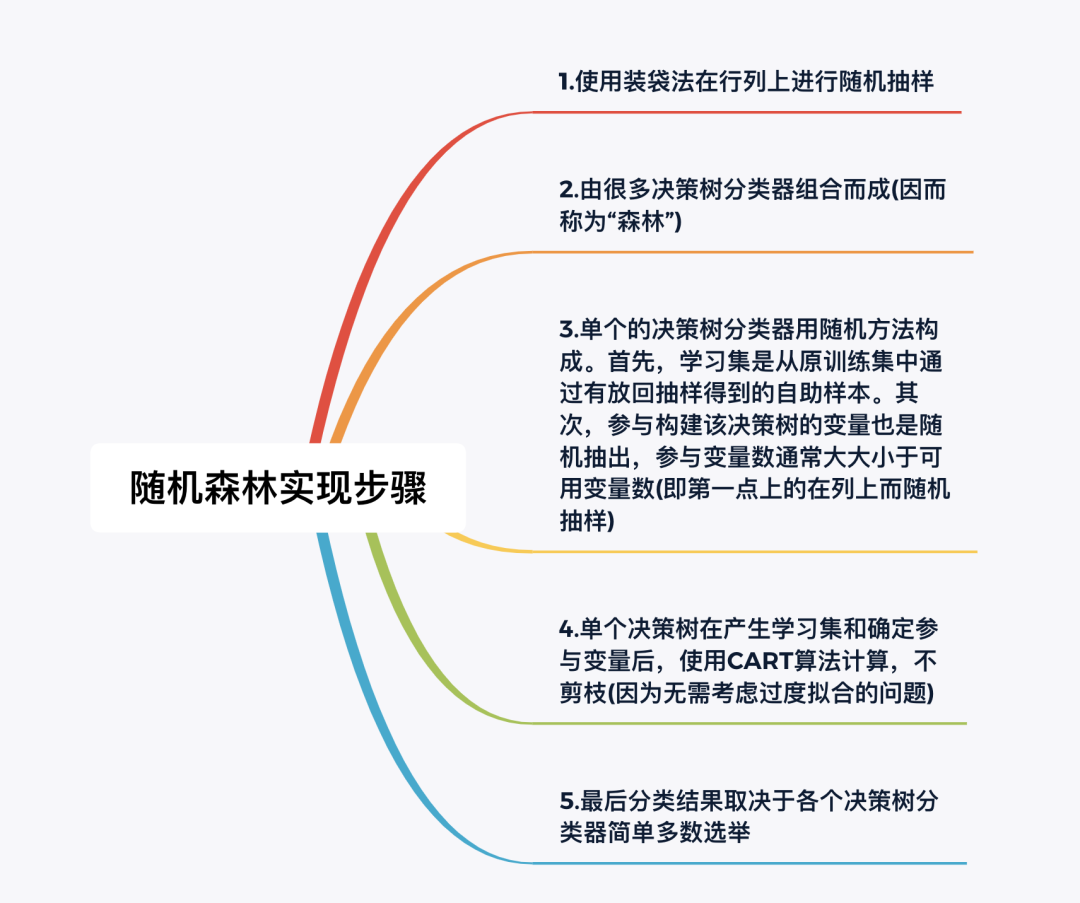

有關(guān)隨機森林算法,本文說明以下幾個問題
問:為什么在列上也要隨機抽樣?
答:在引入筆者最最喜歡的一個比喻之前,先來看一個實際的業(yè)務(wù)場景,來自某城市商業(yè)銀行。我們有一大個電子表格存著大量的歷史數(shù)據(jù),大概50多個變量(50多列),變量們來自幾個不同的公司如人行,電信等(同一個客戶在不同公司),最后希望預(yù)測的是該客戶是否會違約。電子表格組成如下:
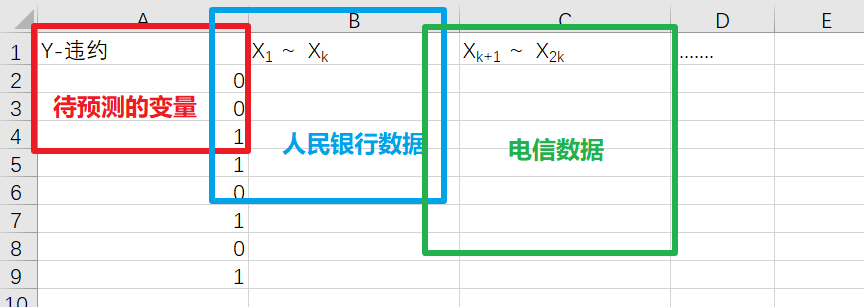
而根據(jù)基礎(chǔ)的業(yè)務(wù)知識可知,與銀行有關(guān)的數(shù)據(jù)中往往會存在許多缺失值,以上圖為例,通常情況下只有待預(yù)測的變量這一列的數(shù)據(jù)是齊全的,畢竟客戶們是否違約這個行為的歷史數(shù)據(jù)很容易查找,但藍(lán)框和綠框這兩部分的缺失值往往較多,而且較隨意,具體隨意程度參見下圖:
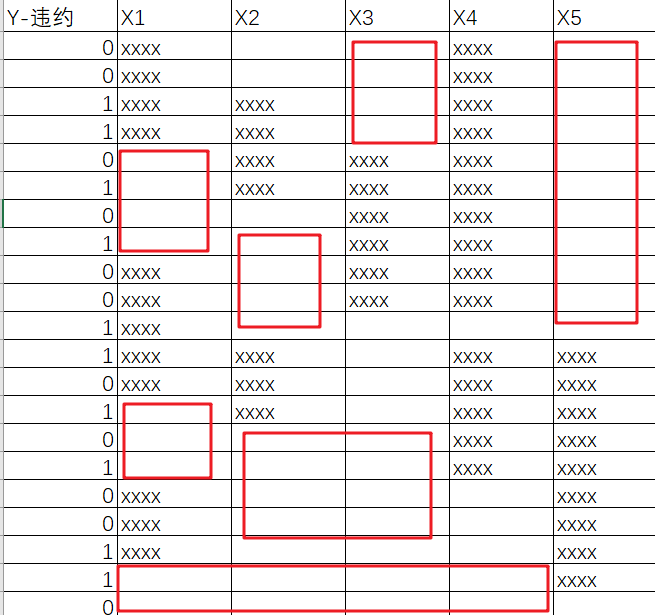
紅框表示數(shù)據(jù)缺失,這里只展示了部分行和部分列數(shù)據(jù),如果這份數(shù)據(jù)表的規(guī)模為 4萬行 * 50列,那這數(shù)據(jù)缺失的分布得有多隨意啊 ???所以,到底該如何充分利用這殘次不齊的數(shù)據(jù)就成了呈待解決的關(guān)鍵問題。這時候就可以祭出超級生動形象的 “島嶼 - 湖泊 - 椰子樹”比喻了:
整個表格看成一座巨大的島嶼,島嶼的長和寬分別對應(yīng)電子表格橫軸長和縱軸的長度
表中缺失的數(shù)據(jù)段看成一個個分布隨意的小湖泊,有數(shù)據(jù)的地方看成陸地
整個小島地底埋藏著巨大的價值(數(shù)據(jù)價值),通過在隨意的種樹(用裝袋法在行列上進(jìn)行隨機抽樣)來吸取地底的養(yǎng)分,畢竟湖泊上種不了樹,所以只要足夠隨機,就總能充分的利用陸地。
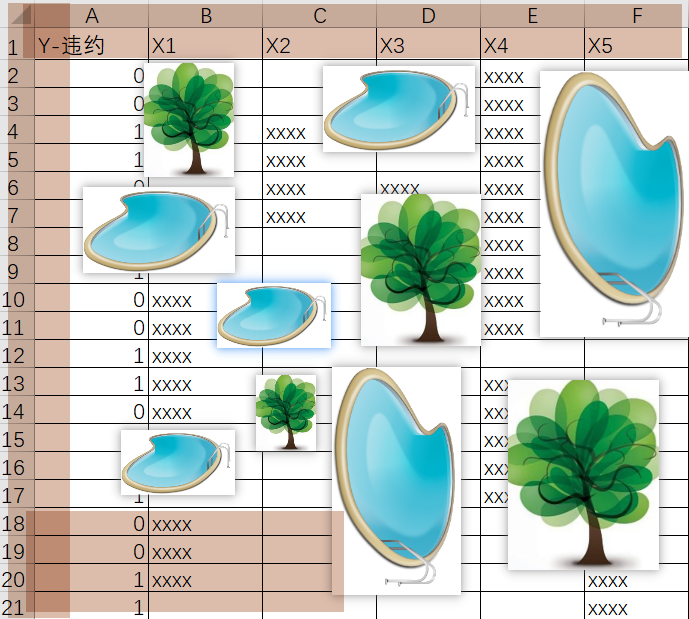
正因為是行列都隨機,才能夠做到真正的把整個數(shù)據(jù)表隨機切分成多份,每個模型使用一份,只要模型的數(shù)量足夠,總有模型能夠在最大程度上獲取數(shù)據(jù)集的價值。而且因變量的分類往往又是極不平衡的,可以參考原理+代碼|手把手教你使用Python實戰(zhàn)反欺詐模型。至于如何將這些種好的樹的信息又再收集,便可以將陸地上比較近的幾棵樹上面再弄一個收集器,把這幾棵樹從陸地上收集到的養(yǎng)分再遞進(jìn)一層匯總,最終實現(xiàn)陸地養(yǎng)分匯總于樹木,樹木養(yǎng)分匯總于收集器,收集器養(yǎng)分匯總于更上層的另一個收集器,最終實現(xiàn)整片數(shù)據(jù)海洋中多個島嶼的信息匯總,這便是周志華團(tuán)隊和螞蟻金服的合作的用分布式深度隨機森林算法檢測套現(xiàn)欺詐。
隨機森林第一步之后的操作完全可以參照集成學(xué)習(xí)——裝袋法中提及的步驟。

問:既然每個模型給出的預(yù)測結(jié)果最后都會被加權(quán),所以隨機森林中每棵決策樹的權(quán)重是多少?
答:隨機森林中每棵決策樹的權(quán)重都是一樣的,如果這個袋子中有 10 棵決策樹(或者其他模型),那每棵樹給出的預(yù)測結(jié)果的權(quán)重便是 1/10,這是隨機森林的特性。如果權(quán)重不一樣的話,便是后續(xù)推文會提及的Adaboost等集成學(xué)習(xí)中的提升分支了。

問:裝袋法中袋子中的模型越多越好嗎?袋中用來訓(xùn)練每個模型的源數(shù)據(jù)比例也是越多越好嗎?
答:袋子中模型多一點好,袋中用來訓(xùn)練每個模型的源數(shù)據(jù)比例小一點好,但這并不代表越多越好與越小越好,還得結(jié)合數(shù)據(jù)集特性和一些深層次的模型算法知識。
裝袋法的優(yōu)勢如下:
準(zhǔn)確率明顯高于組合中任何單個分類器
對于較大的噪音,表現(xiàn)不至于很差,并且具有魯棒性
不容易過度擬合
隨機森林算法的優(yōu)點:
準(zhǔn)確率有時可以和神經(jīng)網(wǎng)絡(luò)媳美,比邏輯回歸高
對錯誤和離群點更加魯棒性
決策樹容易過度擬合的問題會隨著森林的規(guī)模而削弱
大數(shù)據(jù)情況下速度快(分布式),性能好
Python實戰(zhàn)
數(shù)據(jù)探索
本次實戰(zhàn)目標(biāo)為演示隨機森林的用法和調(diào)優(yōu)方法。因為集成學(xué)習(xí)與神經(jīng)網(wǎng)絡(luò)一樣,都屬于解釋性較差的黑盒模型,所以我們無需過分探究數(shù)據(jù)集中每個變量的具體含義,只需關(guān)注最后一個變量broadband即可,爭取通過如年齡,使用時長,支付情況以及流量和通話情況等變量對寬帶客戶是否會續(xù)費做出一個較準(zhǔn)確的預(yù)測。
import?pandas?as?pd
import?numpy?as?np
df?=?pd.read_csv('broadband.csv')?#?寬帶客戶數(shù)據(jù)
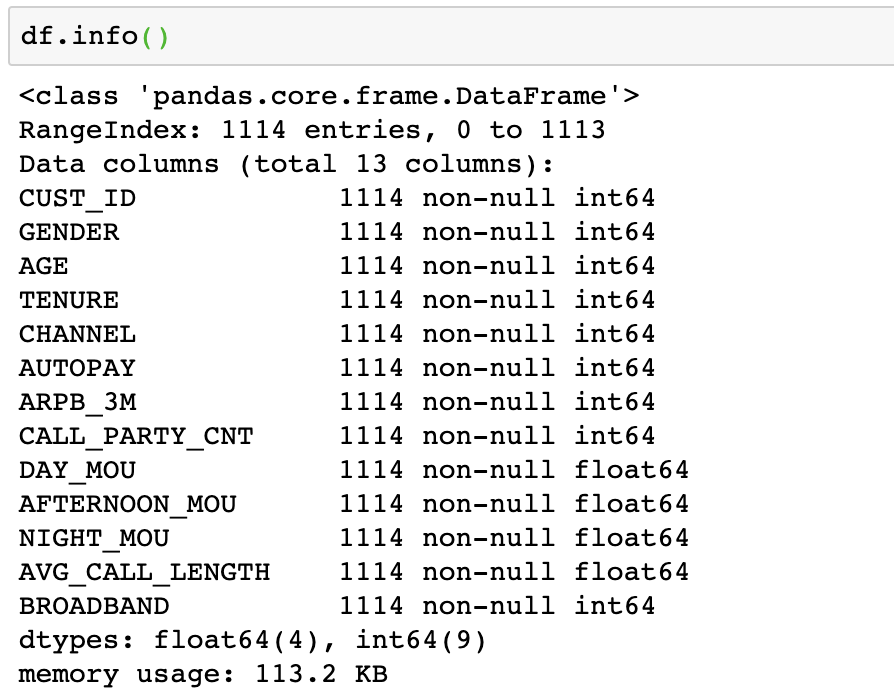
df.head();?df.info()
參數(shù)說明
本代碼文件只為演示隨機森林的用法和調(diào)優(yōu)方法,所以數(shù)據(jù)參數(shù)我們只需關(guān)注最后一個broadband 即可0-離開,1-留存。其他自變量意思可不做探究,畢竟真實工作中的數(shù)據(jù)集也完全不一樣,首先將列名全部小寫
df.rename(str.lower,?axis='columns',?inplace=True)現(xiàn)在查看因變量broadband分布情況,看是否存在不平衡
from?collections?import?Counter
print('Broadband:?',?Counter(df['broadband']))?
## Broadband:? Counter({0: 908, 1: 206})?比較不平衡。
##?根據(jù)原理部分,可知隨機森林是處理數(shù)據(jù)不平衡問題的利器接著拆分測試集與訓(xùn)練集,客戶id沒有用,故丟棄cust_id,
y?=?df['broadband']?
X?=?df.iloc[:,?1:-1]?
from?sklearn.model_selection?import?train_test_split
X_train,?X_test,?y_train,?y_test?=?train_test_split(X,?y,?
????????????????????????????????????test_size=0.4,?random_state=12345)決策樹建模
我們先進(jìn)行完整的決策樹建模來和隨機森林進(jìn)行對比
import?sklearn.tree?as?tree
#?直接使用交叉網(wǎng)格搜索來優(yōu)化決策樹模型,邊訓(xùn)練邊優(yōu)化
from?sklearn.model_selection?import?GridSearchCV
#?網(wǎng)格搜索的參數(shù):正常決策樹建模中的參數(shù)?-?評估指標(biāo),樹的深度,
?##?最小拆分的葉子樣本數(shù)與樹的深度
param_grid?=?{'criterion':?['entropy',?'gini'],
?????????????'max_depth':?[2,?3,?4,?5,?6,?7,?8],
?????????????'min_samples_split':?[4,?8,?12,?16,?20,?24,?28]}?
????????????????#?通常來說,十幾層的樹已經(jīng)是比較深了
clf?=?tree.DecisionTreeClassifier()??#?定義一棵樹
clfcv?=?GridSearchCV(estimator=clf,?param_grid=param_grid,?
????????????????????????????scoring='roc_auc',?cv=4)?
????????#?傳入模型,網(wǎng)格搜索的參數(shù),評估指標(biāo),cv交叉驗證的次數(shù)
??????##?這里也只是定義,還沒有開始訓(xùn)練模型
??????
clfcv.fit(X=X_train,?y=y_train)
#?使用模型來對測試集進(jìn)行預(yù)測
test_est?=?clfcv.predict(X_test)
#?模型評估
import?sklearn.metrics?as?metrics
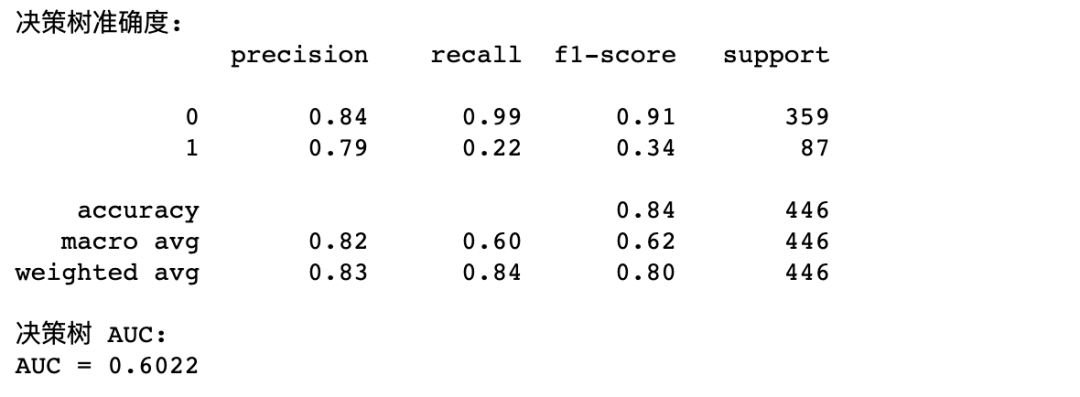
print("決策樹準(zhǔn)確度:")
print(metrics.classification_report(y_test,test_est))?
????????#?該矩陣表格其實作用不大
print("決策樹?AUC:")
fpr_test,?tpr_test,?th_test?=?metrics.roc_curve(y_test,?test_est)
print('AUC?=?%.4f'?%metrics.auc(fpr_test,?tpr_test))
AUC 大于0.5是最基本的要求,可見模型精度還是比較糟糕的,決策樹的調(diào)優(yōu)技巧就不再過多展開,我們將在隨機森林調(diào)優(yōu)部分展示
隨機森林建模
隨機森林建模一樣是使用網(wǎng)格搜索,有關(guān)Python實現(xiàn)隨機森林建模的詳細(xì)參數(shù)解釋可以看代碼的注釋
param_grid?=?{
????'criterion':['entropy','gini'],
????'max_depth':[5,?6,?7,?8],????#?深度:這里是森林中每棵決策樹的深度
????'n_estimators':[11,13,15],??#?決策樹個數(shù)-隨機森林特有參數(shù)
????'max_features':[0.3,0.4,0.5],
?????#?每棵決策樹使用的變量占比-隨機森林特有參數(shù)(結(jié)合原理)
????'min_samples_split':[4,8,12,16]??#?葉子的最小拆分樣本量
}
import?sklearn.ensemble?as?ensemble?#?ensemble?learning:?集成學(xué)習(xí)
rfc?=?ensemble.RandomForestClassifier()
rfc_cv?=?GridSearchCV(estimator=rfc,?param_grid=param_grid,
??????????????????????scoring='roc_auc',?cv=4)
rfc_cv.fit(X_train,?y_train)
#?使用隨機森林對測試集進(jìn)行預(yù)測
test_est?=?rfc_cv.predict(X_test)
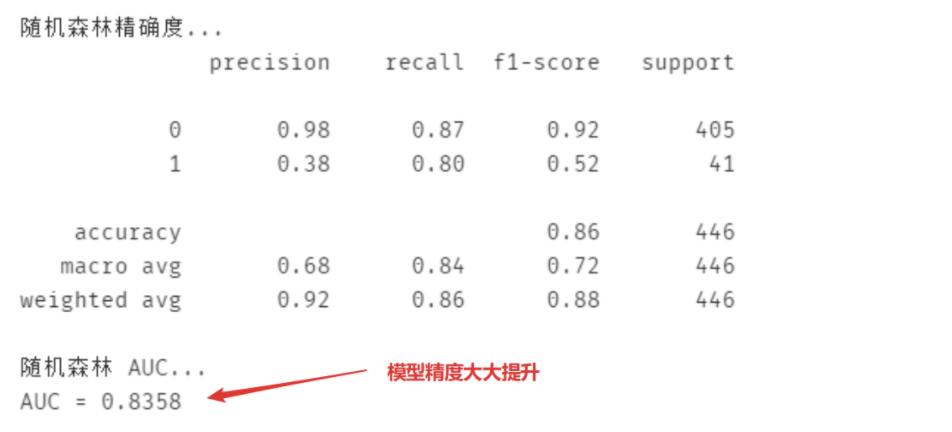
print('隨機森林精確度...')
print(metrics.classification_report(test_est,?y_test))
print('隨機森林?AUC...')
fpr_test,?tpr_test,?th_test?=?metrics.roc_curve(test_est,?y_test)
?????#?構(gòu)造?roc?曲線
print('AUC?=?%.4f'?%metrics.auc(fpr_test,?tpr_test))可以看到,模型的精度大大提升
為什么要打印梯度優(yōu)化給出的最佳參數(shù)?打印梯度優(yōu)化結(jié)果的最佳參數(shù)的目的是為了判斷這個分類模型的各種參數(shù)是否在決策邊界上,簡言之,我們不希望決策邊界限制了這個模型的效果。(通常這時候會先把復(fù)雜度放一邊)

不難發(fā)現(xiàn),參數(shù)max_depth, min_samples_split, 和n_estimators 這三個參數(shù)的范圍設(shè)置可能有限制模型精度的可能,所以需要適當(dāng)調(diào)整
"""
{'criterion':?'gini',
?'max_depth':?8,??在最大值邊界上,所以這個參數(shù)的最大值范圍應(yīng)該再調(diào)大
?'max_features':?0.5,??也在最大值邊界上,說明這個參數(shù)的最小值范圍應(yīng)該再調(diào)大
?'min_samples_split':?4,?同理,在最小邊界上,可考慮把范圍調(diào)小
?'n_estimators':?15?同理,在最大邊界上,可以適當(dāng)調(diào)大范圍
?"""
?#?調(diào)整結(jié)果
?param_grid?=?{
????'criterion':['entropy','gini'],
????'max_depth':[7,?8,?10,?12],?
????#?前面的?5,6?也可以適當(dāng)?shù)娜サ簦凑呀?jīng)沒有用了
????'n_estimators':[11,?13,?15,?17,?19],??#決策樹個數(shù)-隨機森林特有參數(shù)
????'max_features':[0.4,?0.5,?0.6,?0.7],
?????#每棵決策樹使用的變量占比-隨機森林特有參數(shù)
????'min_samples_split':[2,?3,?4,?8,?12,?16]??#?葉子的最小拆分樣本量現(xiàn)在來查看再次建模的結(jié)果

此時都在決策邊界內(nèi)了,但其實調(diào)整參數(shù)是門技術(shù)活,并不只是通過決策邊界這一單一指標(biāo)來調(diào)整,后續(xù)推文會陸續(xù)更新。
小結(jié)
最后總結(jié)一下:隨機森林是集成學(xué)習(xí)中非常經(jīng)典的一種方法,基礎(chǔ)原理簡單,實現(xiàn)優(yōu)雅,可即學(xué)即用。而且隨機森林應(yīng)用十分廣泛,并不只是局限于常見的金融領(lǐng)域,只要數(shù)據(jù)不平衡或者隨機缺失嚴(yán)重,都值得嘗試。如果你也對本文使用的數(shù)據(jù)和代碼感興趣,可以在后臺回復(fù)0726獲取,我們下個案例見。
python爬蟲人工智能大數(shù)據(jù)公眾號

