聚類(lèi)是一種機(jī)器學(xué)習(xí)技術(shù),它涉及到數(shù)據(jù)點(diǎn)的分組。給定一組數(shù)據(jù)點(diǎn),我們可以使用聚類(lèi)算法將每個(gè)數(shù)據(jù)點(diǎn)劃分為一個(gè)特定的組。理論上,同一組中的數(shù)據(jù)點(diǎn)應(yīng)該具有相似的屬性和/或特征,而不同組中的數(shù)據(jù)點(diǎn)應(yīng)該具有高度不同的屬性和/或特征。聚類(lèi)是一種無(wú)監(jiān)督學(xué)習(xí)的方法,是許多領(lǐng)域中常用的統(tǒng)計(jì)數(shù)據(jù)分析技術(shù)。
在數(shù)據(jù)科學(xué)中,我們可以使用聚類(lèi)分析從我們的數(shù)據(jù)中獲得一些有價(jià)值的見(jiàn)解。在這篇文章中,我們將研究5種流行的聚類(lèi)算法以及它們的優(yōu)缺點(diǎn)。
K-MEANS聚類(lèi)算法
K-Means聚類(lèi)算法可能是大家最熟悉的聚類(lèi)算法。它出現(xiàn)在很多介紹性的數(shù)據(jù)科學(xué)和機(jī)器學(xué)習(xí)課程中。在代碼中很容易理解和實(shí)現(xiàn)!請(qǐng)看下面的圖表。
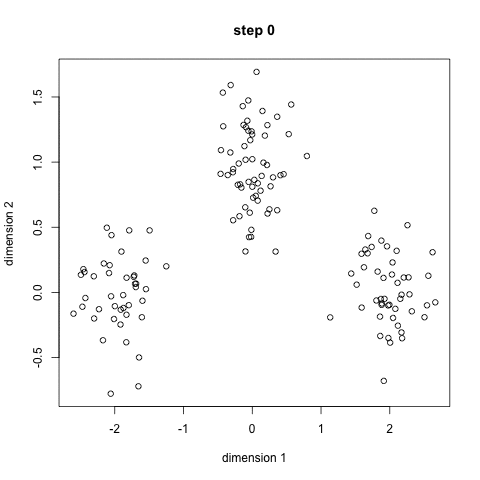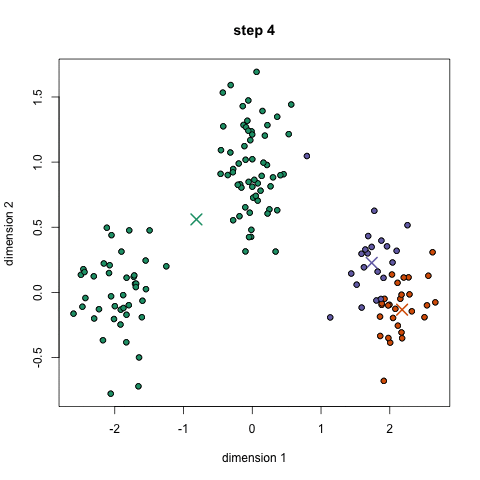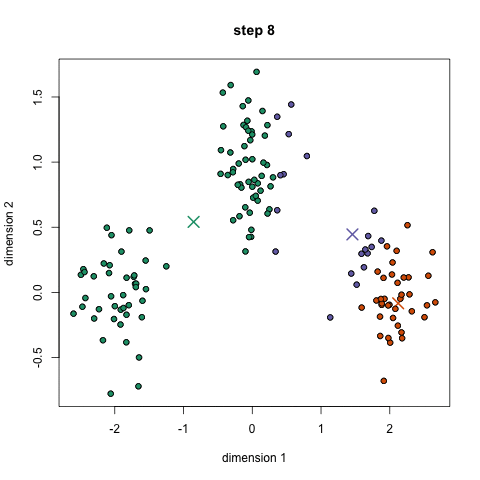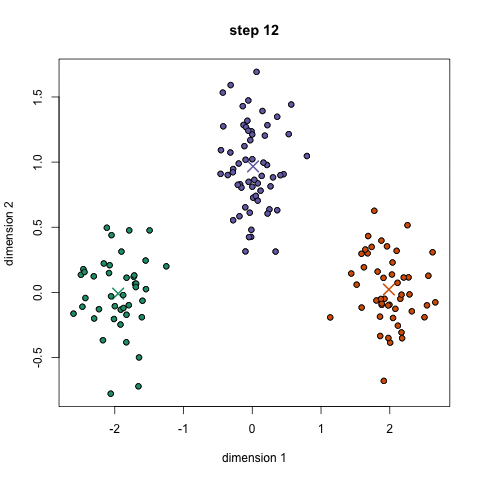
K-Means聚類(lèi)
1.首先,我們選擇一些類(lèi)/組來(lái)使用并隨機(jī)地初始化它們各自的中心點(diǎn)。要想知道要使用的類(lèi)的數(shù)量,最好快速地查看一下數(shù)據(jù),并嘗試識(shí)別任何不同的分組。中心點(diǎn)是與每個(gè)數(shù)據(jù)點(diǎn)向量相同長(zhǎng)度的向量,在上面的圖形中是“X”。
2.每個(gè)數(shù)據(jù)點(diǎn)通過(guò)計(jì)算點(diǎn)和每個(gè)組中心之間的距離進(jìn)行分類(lèi),然后將這個(gè)點(diǎn)分類(lèi)為最接近它的組。
3.基于這些分類(lèi)點(diǎn),我們通過(guò)取組中所有向量的均值來(lái)重新計(jì)算組中心。
4.對(duì)一組迭代重復(fù)這些步驟。你還可以選擇隨機(jī)初始化組中心幾次,然后選擇那些看起來(lái)對(duì)它提供了最好結(jié)果的來(lái)運(yùn)行。
K-Means聚類(lèi)算法的優(yōu)勢(shì)在于它的速度非常快,因?yàn)槲覀兯龅闹皇怯?jì)算點(diǎn)和群中心之間的距離;它有一個(gè)線性復(fù)雜度O(n)。
另一方面,K-Means也有幾個(gè)缺點(diǎn)。首先,你必須選擇有多少組/類(lèi)。這并不是不重要的事,理想情況下,我們希望它能幫我們解決這些問(wèn)題,因?yàn)樗年P(guān)鍵在于從數(shù)據(jù)中獲得一些啟示。K-Means也從隨機(jī)選擇的聚類(lèi)中心開(kāi)始,因此在不同的算法運(yùn)行中可能產(chǎn)生不同的聚類(lèi)結(jié)果。因此,結(jié)果可能是不可重復(fù)的,并且缺乏一致性。其他聚類(lèi)方法更加一致。
K-Medians是另一種與K-Means有關(guān)的聚類(lèi)算法,除了使用均值的中間值來(lái)重新計(jì)算組中心點(diǎn)以外,這種方法對(duì)離群值的敏感度較低(因?yàn)槭褂弥兄担珜?duì)于較大的數(shù)據(jù)集來(lái)說(shuō),它要慢得多,因?yàn)樵谟?jì)算中值向量時(shí),每次迭代都需要進(jìn)行排序。
均值偏移聚類(lèi)算法
均值偏移(Mean shift)聚類(lèi)算法是一種基于滑動(dòng)窗口(sliding-window)的算法,它試圖找到密集的數(shù)據(jù)點(diǎn)。而且,它還是一種基于中心的算法,它的目標(biāo)是定位每一組群/類(lèi)的中心點(diǎn),通過(guò)更新中心點(diǎn)的候選點(diǎn)來(lái)實(shí)現(xiàn)滑動(dòng)窗口中的點(diǎn)的平均值。這些候選窗口在后期處理階段被過(guò)濾,以消除幾乎重復(fù)的部分,形成最后一組中心點(diǎn)及其對(duì)應(yīng)的組。請(qǐng)看下面的圖表。
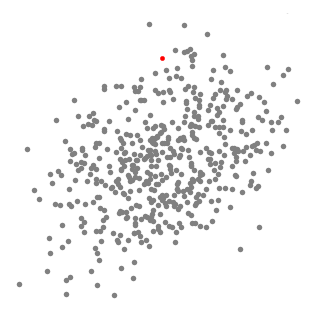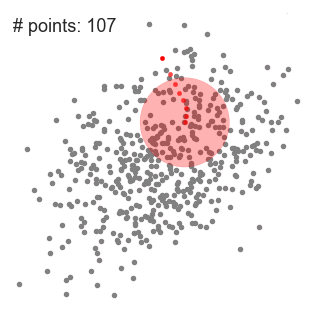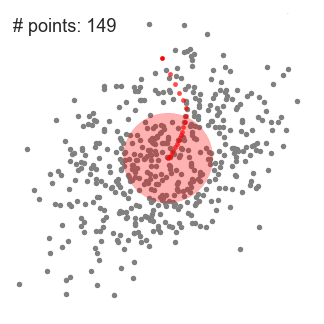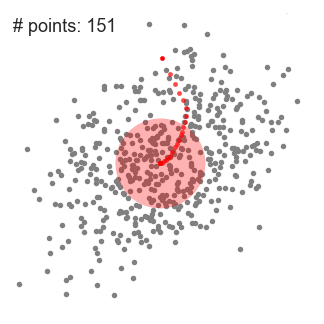
單滑動(dòng)窗口的均值偏移聚類(lèi)
1.為了解釋這一變化,我們將考慮二維空間中的一組點(diǎn)(就像上面的例子)。我們從一個(gè)以點(diǎn)C(隨機(jī)選擇)為中心的圓形滑窗開(kāi)始,以半徑r為內(nèi)核。均值偏移是一種爬山算法(hill climbing algorithm),它需要在每個(gè)步驟中反復(fù)地將這個(gè)內(nèi)核移動(dòng)到一個(gè)更高的密度區(qū)域,直到收斂。
2.在每一次迭代中,滑動(dòng)窗口會(huì)移向密度較高的區(qū)域,將中心點(diǎn)移動(dòng)到窗口內(nèi)的點(diǎn)的平均值(因此得名)。滑動(dòng)窗口中的密度與它內(nèi)部的點(diǎn)的數(shù)量成比例。自然地,通過(guò)移向窗口中點(diǎn)的平均值,它將逐漸向更高的點(diǎn)密度方向移動(dòng)。
3.我們繼續(xù)根據(jù)均值移動(dòng)滑動(dòng)窗口,直到?jīng)]有方向移動(dòng)可以容納內(nèi)核中的更多點(diǎn)。看看上面的圖表;我們一直在移動(dòng)這個(gè)圓,直到我們不再增加密度(也就是窗口中的點(diǎn)數(shù))。
4.步驟1到3的過(guò)程是用許多滑動(dòng)窗口完成的,直到所有的點(diǎn)都位于一個(gè)窗口內(nèi)。當(dāng)多個(gè)滑動(dòng)窗口重疊的時(shí)候,包含最多點(diǎn)的窗口會(huì)被保留。然后,數(shù)據(jù)點(diǎn)根據(jù)它們所在的滑動(dòng)窗口聚類(lèi)。
下面展示了從端到端所有滑動(dòng)窗口的整個(gè)過(guò)程的演示。每個(gè)黑點(diǎn)代表一個(gè)滑動(dòng)窗口的質(zhì)心,每個(gè)灰色點(diǎn)都是一個(gè)數(shù)據(jù)點(diǎn)。

均值偏移聚類(lèi)的整個(gè)過(guò)程
與K-Means聚類(lèi)相比,均值偏移不需要選擇聚類(lèi)的數(shù)量,因?yàn)樗鼤?huì)自動(dòng)地發(fā)現(xiàn)這一點(diǎn)。這是一個(gè)巨大的優(yōu)勢(shì)。聚類(lèi)中心收斂于最大密度點(diǎn)的事實(shí)也是非常可取的,因?yàn)樗浅V庇^地理解并適合于一種自然數(shù)據(jù)驅(qū)動(dòng)。缺點(diǎn)是選擇窗口大小/半徑r是非常關(guān)鍵的,所以不能疏忽。
DBSCAN聚類(lèi)算法
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一個(gè)比較有代表性的基于密度的聚類(lèi)算法,類(lèi)似于均值轉(zhuǎn)移聚類(lèi)算法,但它有幾個(gè)顯著的優(yōu)點(diǎn)。
DBSCAN笑臉聚類(lèi)
1.DBSCAN以一個(gè)從未訪問(wèn)過(guò)的任意起始數(shù)據(jù)點(diǎn)開(kāi)始。這個(gè)點(diǎn)的鄰域是用距離ε(所有在ε距離的點(diǎn)都是鄰點(diǎn))來(lái)提取的。
2.如果在這個(gè)鄰域中有足夠數(shù)量的點(diǎn)(根據(jù) minPoints),那么聚類(lèi)過(guò)程就開(kāi)始了,并且當(dāng)前的數(shù)據(jù)點(diǎn)成為新聚類(lèi)中的第一個(gè)點(diǎn)。否則,該點(diǎn)將被標(biāo)記為噪聲(稍后這個(gè)噪聲點(diǎn)可能會(huì)成為聚類(lèi)的一部分)。在這兩種情況下,這一點(diǎn)都被標(biāo)記為“訪問(wèn)(visited)”。
3.對(duì)于新聚類(lèi)中的第一個(gè)點(diǎn),其ε距離附近的點(diǎn)也會(huì)成為同一聚類(lèi)的一部分。這一過(guò)程使在ε鄰近的所有點(diǎn)都屬于同一個(gè)聚類(lèi),然后重復(fù)所有剛剛添加到聚類(lèi)組的新點(diǎn)。
4.步驟2和步驟3的過(guò)程將重復(fù),直到聚類(lèi)中的所有點(diǎn)都被確定,就是說(shuō)在聚類(lèi)附近的所有點(diǎn)都已被訪問(wèn)和標(biāo)記。
5.一旦我們完成了當(dāng)前的聚類(lèi),就會(huì)檢索并處理一個(gè)新的未訪問(wèn)點(diǎn),這將導(dǎo)致進(jìn)一步的聚類(lèi)或噪聲的發(fā)現(xiàn)。這個(gè)過(guò)程不斷地重復(fù),直到所有的點(diǎn)被標(biāo)記為訪問(wèn)。因?yàn)樵谒械狞c(diǎn)都被訪問(wèn)過(guò)之后,每一個(gè)點(diǎn)都被標(biāo)記為屬于一個(gè)聚類(lèi)或者是噪音。
DBSCAN比其他聚類(lèi)算法有一些優(yōu)勢(shì)。首先,它不需要一個(gè)預(yù)設(shè)定的聚類(lèi)數(shù)量。它還將異常值識(shí)別為噪聲,而不像均值偏移聚類(lèi)算法,即使數(shù)據(jù)點(diǎn)非常不同,它也會(huì)將它們放入一個(gè)聚類(lèi)中。此外,它還能很好地找到任意大小和任意形狀的聚類(lèi)。
DBSCAN的主要缺點(diǎn)是,當(dāng)聚類(lèi)具有不同的密度時(shí),它的性能不像其他聚類(lèi)算法那樣好。這是因?yàn)楫?dāng)密度變化時(shí),距離閾值ε和識(shí)別鄰近點(diǎn)的minPoints的設(shè)置會(huì)隨著聚類(lèi)的不同而變化。這種缺點(diǎn)也會(huì)出現(xiàn)在非常高維的數(shù)據(jù)中,因?yàn)榫嚯x閾值ε變得難以估計(jì)。
使用高斯混合模型(GMM)的期望最大化(EM)聚類(lèi)
K-Means的一個(gè)主要缺點(diǎn)是它對(duì)聚類(lèi)中心的平均值的使用很簡(jiǎn)單幼稚。我們可以通過(guò)看下面的圖片來(lái)了解為什么這不是最好的方法。在左邊看起來(lái)很明顯的是,有兩個(gè)圓形的聚類(lèi),不同的半徑以相同的平均值為中心。K-Means無(wú)法處理,因?yàn)榫垲?lèi)的均值非常接近。在聚類(lèi)不是循環(huán)的情況下,K-Means也會(huì)失敗,這也是使用均值作為聚類(lèi)中心的結(jié)果。

K-Means的兩個(gè)失敗案例
高斯混合模型(GMMs)比K-Means更具靈活性。使用高斯混合模型,我們可以假設(shè)數(shù)據(jù)點(diǎn)是高斯分布的;比起說(shuō)它們是循環(huán)的,這是一個(gè)不那么嚴(yán)格的假設(shè)。這樣,我們就有兩個(gè)參數(shù)來(lái)描述聚類(lèi)的形狀:平均值和標(biāo)準(zhǔn)差!以二維的例子為例,這意味著聚類(lèi)可以采用任何形式的橢圓形狀(因?yàn)樵趚和y方向上都有標(biāo)準(zhǔn)差)。因此,每個(gè)高斯分布可歸屬于一個(gè)單獨(dú)的聚類(lèi)。
為了找到每個(gè)聚類(lèi)的高斯分布的參數(shù)(例如平均值和標(biāo)準(zhǔn)差)我們將使用一種叫做期望最大化(EM)的優(yōu)化算法。看看下面的圖表,就可以看到高斯混合模型是被擬合到聚類(lèi)上的。然后,我們可以繼續(xù)進(jìn)行期望的過(guò)程——使用高斯混合模型實(shí)現(xiàn)最大化聚類(lèi)。
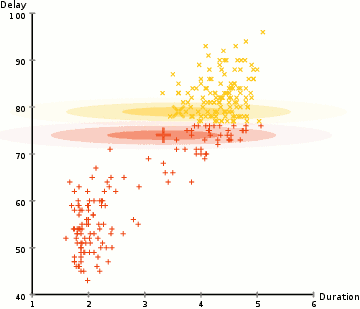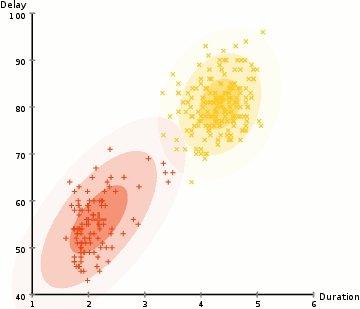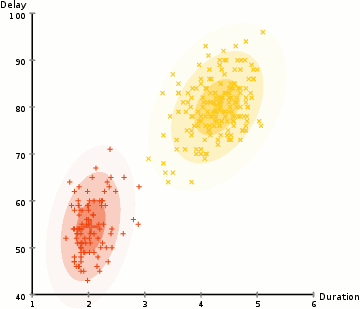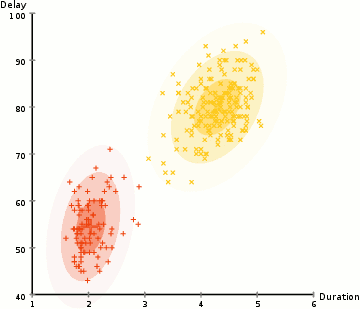
使用高斯混合模型來(lái)期望最大化聚類(lèi)
1.我們首先選擇聚類(lèi)的數(shù)量(如K-Means所做的那樣),然后隨機(jī)初始化每個(gè)聚類(lèi)的高斯分布參數(shù)。通過(guò)快速查看數(shù)據(jù),可以嘗試為初始參數(shù)提供良好的猜測(cè)。注意,在上面的圖表中可以看到,這并不是100%的必要,因?yàn)楦咚归_(kāi)始時(shí)的表現(xiàn)非常不好,但是很快就被優(yōu)化了。
2.給定每個(gè)聚類(lèi)的高斯分布,計(jì)算每個(gè)數(shù)據(jù)點(diǎn)屬于特定聚類(lèi)的概率。一個(gè)點(diǎn)離高斯中心越近,它就越有可能屬于那個(gè)聚類(lèi)。這應(yīng)該是很直觀的,因?yàn)橛幸粋€(gè)高斯分布,我們假設(shè)大部分的數(shù)據(jù)都離聚類(lèi)中心很近。
3.基于這些概率,我們?yōu)楦咚狗植加?jì)算一組新的參數(shù),這樣我們就能最大程度地利用聚類(lèi)中的數(shù)據(jù)點(diǎn)的概率。我們使用數(shù)據(jù)點(diǎn)位置的加權(quán)和來(lái)計(jì)算這些新參數(shù),權(quán)重是屬于該特定聚類(lèi)的數(shù)據(jù)點(diǎn)的概率。為了解釋這一點(diǎn),我們可以看一下上面的圖,特別是黃色的聚類(lèi)作為例子。分布在第一次迭代中是隨機(jī)的,但是我們可以看到大多數(shù)的黃色點(diǎn)都在這個(gè)分布的右邊。當(dāng)我們計(jì)算一個(gè)由概率加權(quán)的和,即使在中心附近有一些點(diǎn),它們中的大部分都在右邊。因此,自然分布的均值更接近于這些點(diǎn)。我們還可以看到,大多數(shù)點(diǎn)都是“從右上角到左下角”。因此,標(biāo)準(zhǔn)差的變化是為了創(chuàng)造一個(gè)更符合這些點(diǎn)的橢圓,從而使概率的總和最大化。
步驟2和3被迭代地重復(fù),直到收斂,在那里,分布不會(huì)從迭代到迭代這個(gè)過(guò)程中變化很多。
使用高斯混合模型有兩個(gè)關(guān)鍵的優(yōu)勢(shì)。首先,高斯混合模型在聚類(lèi)協(xié)方差方面比K-Means要靈活得多;根據(jù)標(biāo)準(zhǔn)差參數(shù),聚類(lèi)可以采用任何橢圓形狀,而不是局限于圓形。K-Means實(shí)際上是高斯混合模型的一個(gè)特例,每個(gè)聚類(lèi)在所有維度上的協(xié)方差都接近0。其次,根據(jù)高斯混合模型的使用概率,每個(gè)數(shù)據(jù)點(diǎn)可以有多個(gè)聚類(lèi)。因此,如果一個(gè)數(shù)據(jù)點(diǎn)位于兩個(gè)重疊的聚類(lèi)的中間,通過(guò)說(shuō)X%屬于1類(lèi),而y%屬于2類(lèi),我們可以簡(jiǎn)單地定義它的類(lèi)。
層次聚類(lèi)算法
層次聚類(lèi)算法實(shí)際上分為兩類(lèi):自上而下或自下而上。自下而上的算法在一開(kāi)始就將每個(gè)數(shù)據(jù)點(diǎn)視為一個(gè)單一的聚類(lèi),然后依次合并(或聚集)類(lèi),直到所有類(lèi)合并成一個(gè)包含所有數(shù)據(jù)點(diǎn)的單一聚類(lèi)。因此,自下而上的層次聚類(lèi)稱(chēng)為合成聚類(lèi)或HAC。聚類(lèi)的層次結(jié)構(gòu)用一棵樹(shù)(或樹(shù)狀圖)表示。樹(shù)的根是收集所有樣本的唯一聚類(lèi),而葉子是只有一個(gè)樣本的聚類(lèi)。在繼續(xù)學(xué)習(xí)算法步驟之前,先查看下面的圖表。
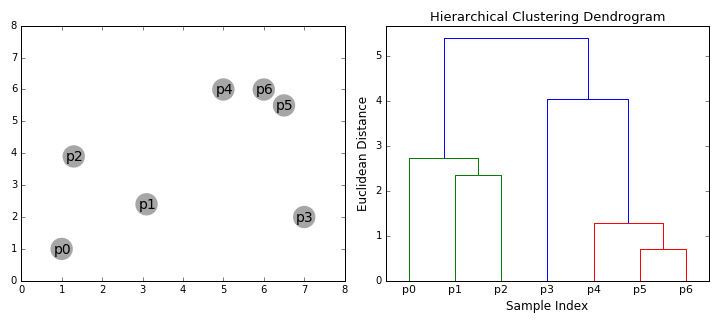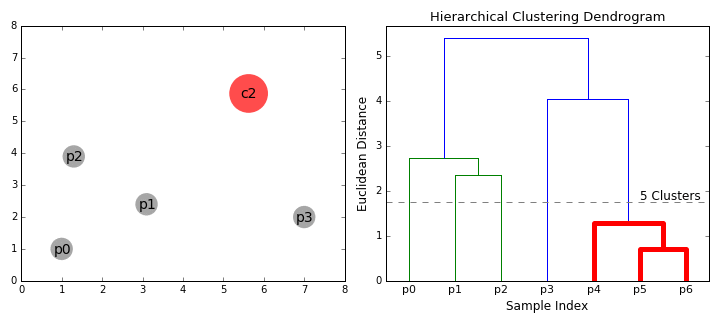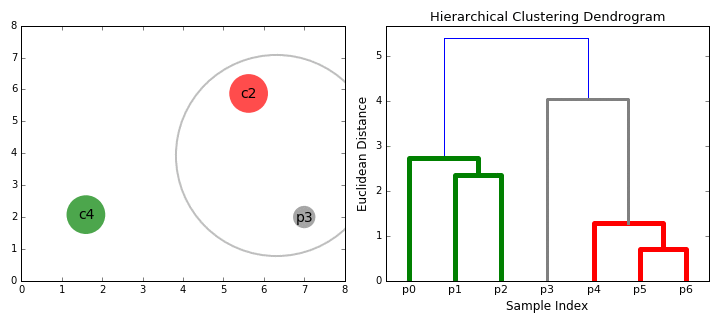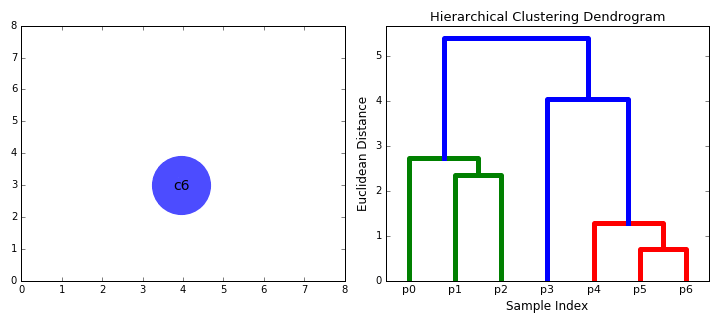
合成聚類(lèi)
1.我們首先將每個(gè)數(shù)據(jù)點(diǎn)作為一個(gè)單獨(dú)的聚類(lèi)進(jìn)行處理。如果我們的數(shù)據(jù)集有X個(gè)數(shù)據(jù)點(diǎn),那么我們就有了X個(gè)聚類(lèi)。然后我們選擇一個(gè)度量?jī)蓚€(gè)聚類(lèi)之間距離的距離度量。作為一個(gè)示例,我們將使用平均連接(average linkage)聚類(lèi),它定義了兩個(gè)聚類(lèi)之間的距離,即第一個(gè)聚類(lèi)中的數(shù)據(jù)點(diǎn)和第二個(gè)聚類(lèi)中的數(shù)據(jù)點(diǎn)之間的平均距離。
2.在每次迭代中,我們將兩個(gè)聚類(lèi)合并為一個(gè)。將兩個(gè)聚類(lèi)合并為具有最小平均連接的組。比如說(shuō)根據(jù)我們選擇的距離度量,這兩個(gè)聚類(lèi)之間的距離最小,因此是最相似的,應(yīng)該組合在一起。
3.重復(fù)步驟2直到我們到達(dá)樹(shù)的根。我們只有一個(gè)包含所有數(shù)據(jù)點(diǎn)的聚類(lèi)。通過(guò)這種方式,我們可以選擇最終需要多少個(gè)聚類(lèi),只需選擇何時(shí)停止合并聚類(lèi),也就是我們停止建造這棵樹(shù)的時(shí)候!
層次聚類(lèi)算法不要求我們指定聚類(lèi)的數(shù)量,我們甚至可以選擇哪個(gè)聚類(lèi)看起來(lái)最好。此外,該算法對(duì)距離度量的選擇不敏感;它們的工作方式都很好,而對(duì)于其他聚類(lèi)算法,距離度量的選擇是至關(guān)重要的。層次聚類(lèi)方法的一個(gè)特別好的用例是,當(dāng)?shù)讓訑?shù)據(jù)具有層次結(jié)構(gòu)時(shí),你可以恢復(fù)層次結(jié)構(gòu);而其他的聚類(lèi)算法無(wú)法做到這一點(diǎn)。層次聚類(lèi)的優(yōu)點(diǎn)是以低效率為代價(jià)的,因?yàn)樗哂蠴(n3)的時(shí)間復(fù)雜度,與K-Means和高斯混合模型的線性復(fù)雜度不同。
 下載APP
下載APP