【機器學(xué)習(xí)】用 Hyperopt 和 Plotly 可視化超參數(shù)優(yōu)化
來源:@公眾號:數(shù)據(jù)STUDIO
在這篇文章中,云朵君將演示如何創(chuàng)建超參數(shù)設(shè)置的有效交互式可視化,使我們能夠了解在超參數(shù)優(yōu)化期間嘗試的超參數(shù)設(shè)置之間的關(guān)系。本文的第 1 部分將使用 hyperopt 設(shè)置一個簡單的超參數(shù)優(yōu)化示例。在第 2 部分中,我們將展示如何使用Plotly創(chuàng)建由第 1 部分中的超參數(shù)優(yōu)化生成的數(shù)據(jù)的交互式可視化。
hyperopt就是其中一個廣泛使用的超參數(shù)優(yōu)化框架包,它允許數(shù)據(jù)科學(xué)家通過定義目標(biāo)函數(shù)和聲明搜索空間來利用幾種強大的算法進行超參數(shù)優(yōu)化。然而,依靠這些工具可以將超參數(shù)選擇變成一個“黑匣子”,這也導(dǎo)致了很難解釋為什么一組特定的超參數(shù)最適合一個特定問題的特定模型。克服這些算法的“黑匣子”性質(zhì)的一種方法,是可視化在超參數(shù)優(yōu)化期間嘗試過的超參數(shù)設(shè)置的歷史,以幫助識別運行良好的超參數(shù)設(shè)置的潛在趨勢。

寫在前面
這篇文章假設(shè)讀者熟悉超參數(shù)優(yōu)化的概念。此外,盡管我們將創(chuàng)建一個示例超參數(shù)優(yōu)化來生成可視化所需要的數(shù)據(jù),但我們不會詳細介紹此優(yōu)化,因為本文的目的不是成為有關(guān) hyperopt 的教程;這里有個不錯的hyperopt 文檔英文教程[1]。
為簡潔起見,代碼示例將假設(shè)所有必要的導(dǎo)入都已運行。作為參考,這里是代碼示例所需的完整導(dǎo)入集:
from?functools?import?partial
from?pprint?import?pprint
import?numpy?as?np
import?pandas?as?pd
from?hyperopt?import?fmin,?hp,?space_eval,?tpe,?STATUS_OK,?Trials
from?hyperopt.pyll?import?scope,?stochastic
from?plotly?import?express?as?px
from?plotly?import?graph_objects?as?go
from?plotly?import?offline?as?pyo
from?sklearn.datasets?import?load_boston
from?sklearn.ensemble?import?GradientBoostingRegressor,?RandomForestRegressor
from?sklearn.metrics?import?make_scorer,?mean_squared_error
from?sklearn.model_selection?import?cross_val_score,?KFold
from?sklearn.utils?import?check_random_state
pyo.init_notebook_mode()
使用 hyperopt 超參數(shù)優(yōu)化示例
在我們使用 Plotly 進行可視化之前,我們需要從 hyperopt 生成一些超參數(shù)優(yōu)化數(shù)據(jù)供我們可視化。我們需要遵循四個關(guān)鍵步驟來使用 hyperopt 設(shè)置超參數(shù)優(yōu)化:
選擇和加載數(shù)據(jù)集 聲明超參數(shù)搜索空間 定義目標(biāo)函數(shù) 運行超參數(shù)優(yōu)化
我們將提供每個步驟的簡要描述以及示例代碼,但我們不會詳細說明具體選擇的合理性,因為這種超參數(shù)優(yōu)化的目標(biāo)只是為我們生成可視化數(shù)據(jù)。
選擇和加載數(shù)據(jù)集
我們將使用UCI[2]波士頓數(shù)據(jù)集作為我們的超參數(shù)優(yōu)化的示例數(shù)據(jù)集。UCI 波士頓數(shù)據(jù)集的特征是各種社區(qū)特征,目標(biāo)是該社區(qū)房屋的中值。Scikit-learn 提供了一個方便的包裝函數(shù),名為load_boston。我們將使用此函數(shù)將數(shù)據(jù)集加載到 Pandas 數(shù)據(jù)框中,如下所示:
MEDIAN_HOME_VALUE?=?"median_home_value"
#?使用?sklearn?的輔助函數(shù)加載波士頓數(shù)據(jù)集
boston_dataset?=?load_boston()
#?將數(shù)據(jù)轉(zhuǎn)換為?Pandas?數(shù)據(jù)框
data?=?np.concatenate(
????[boston_dataset["data"],?boston_dataset["target"][...,?np.newaxis]],
????axis=1,
)
features,?target?=?boston_dataset["feature_names"],?MEDIAN_HOME_VALUE
columns?=?np.concatenate([features,?[target]])
boston_dataset_df?=?pd.DataFrame(data,?columns=columns)
boston_dataset_df
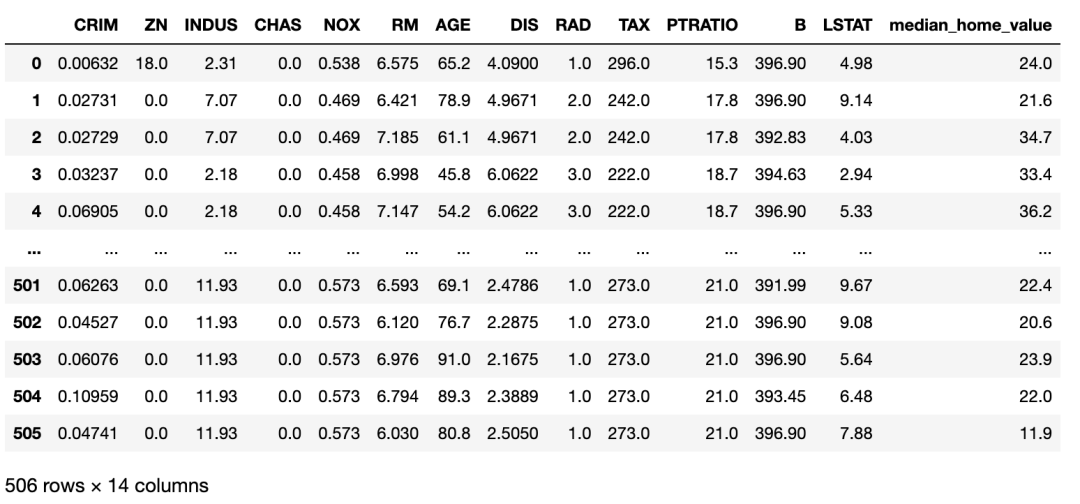
定義超參數(shù)搜索空間
由于該數(shù)據(jù)集的目標(biāo)是連續(xù)的,我們將要比較幾個不同的回歸模型。我們將設(shè)置超參數(shù)優(yōu)化來比較兩種類型的模型:隨機森林回歸器和梯度提升回歸器(可以閱讀文檔戳??集成算法 | 隨機森林回歸模型)。隨機森林回歸器將允許 hyperopt 調(diào)整樹的數(shù)量和每棵樹的最大深度。除了樹的數(shù)量和每棵樹的最大深度之外,梯度提升回歸器將允許 hyperopt 調(diào)整學(xué)習(xí)率。以下字典以 hyperopt 預(yù)期的格式聲明此超參數(shù)搜索空間:
#?定義常量字符串,我們將在下面的“search space”字典中用作鍵。
#?注意,我在整個過程中使用的約定是,
#?用一個匹配該字符串的變量來表示字符串中的字符,只是變量中的字符是大寫的。
#?這種約定允許我們在代碼中遇到這些變量時很容易解釋它們的含義。
#?例如,我們知道變量' MODEL '包含字符串" MODEL "。
#?用變量表示字符串的這種模式允許我在代碼中重復(fù)使用同一個字符串時避免鍵入錯誤,
#?因為在變量名中鍵入錯誤將被檢查器捕獲為錯誤。
GRADIENT_BOOSTING_REGRESSOR?=?"gradient_boosting_regressor"
KWARGS?=?"kwargs"
LEARNING_RATE?=?"learning_rate"
LINEAR_REGRESSION?=?"linear_regression"
MAX_DEPTH?=?"max_depth"
MODEL?=?"model"
MODEL_CHOICE?=?"model_choice"
NORMALIZE?=?"normalize"
N_ESTIMATORS?=?"n_estimators"
RANDOM_FOREST_REGRESSOR?=?"random_forest_regressor"
RANDOM_STATE?=?"random_state"
#?聲明隨機森林回歸模型的搜索空間。
random_forest_regressor?=?{
????MODEL:?RANDOM_FOREST_REGRESSOR,
???#?我將模型參數(shù)定義為一個單獨的字典,以便我們可以將參數(shù)輸入
???#?帶有字典解包的模型的`__init__`。參見?`sample_to_model`?函數(shù)
???#?與目標(biāo)函數(shù)一起定義以查看此操作
????KWARGS:?{
????????N_ESTIMATORS:?scope.int(
????????????hp.quniform(f"{RANDOM_FOREST_REGRESSOR}__{N_ESTIMATORS}",?50,?150,?1)
????????),
????????MAX_DEPTH:?scope.int(
????????????hp.quniform(f"{RANDOM_FOREST_REGRESSOR}__{MAX_DEPTH}",?2,?12,?1)
????????),
????????RANDOM_STATE:?0,
????},
}
#?聲明梯度提升回歸模型的搜索空間,
#?結(jié)構(gòu)與隨機森林回歸搜索空間相同。
gradient_boosting_regressor?=?{
????MODEL:?GRADIENT_BOOSTING_REGRESSOR,
????KWARGS:?{
????????LEARNING_RATE:?scope.float(
????????????hp.uniform(f"{GRADIENT_BOOSTING_REGRESSOR}__{LEARNING_RATE}",?0.01,?0.15,)
????????),??#?lower?learning?rate
????????N_ESTIMATORS:?scope.int(
????????????hp.quniform(f"{GRADIENT_BOOSTING_REGRESSOR}__{N_ESTIMATORS}",?50,?150,?1)
????????),
????????MAX_DEPTH:?scope.int(
????????????hp.quniform(f"{GRADIENT_BOOSTING_REGRESSOR}__{MAX_DEPTH}",?2,?12,?1)
????????),
????????RANDOM_STATE:?0,
????},
}
#?將兩個模型搜索空間與兩個模型之間的頂級“choice”結(jié)合起來,得到最終的搜索空間。
space?=?{
????MODEL_CHOICE:?hp.choice(
????????MODEL_CHOICE,?[random_forest_regressor,?gradient_boosting_regressor,],
????)
}
定義目標(biāo)函數(shù)
對于目標(biāo)函數(shù),我們將通過十折交叉驗證計算數(shù)據(jù)集每個實例的均方誤差。我們將打印折疊的平均均方誤差作為損失。下面的代碼定義了這個目標(biāo):
#?定義幾個額外的變量來表示字符串。注意,這段代碼期望我們能夠
#?訪問之前在"search space"代碼片段中定義的所有變量。
LOSS?=?"loss"
STATUS?=?"status"
#?從字符串名稱映射到模型類定義對象,我們將使用該對象
#?從hyperopt搜索空間生成的樣本創(chuàng)建模型的初始化版本。
MODELS?=?{
????GRADIENT_BOOSTING_REGRESSOR:?GradientBoostingRegressor,
????RANDOM_FOREST_REGRESSOR:?RandomForestRegressor,
}
#?創(chuàng)建一個我們將在目標(biāo)中使用的評分函數(shù)
mse_scorer?=?make_scorer(mean_squared_error)
#?從hyperopt生成的示例轉(zhuǎn)換為初始化模型的輔助函數(shù)。
#?注意,因為我們在搜索空間聲明中將模型類型和模型關(guān)鍵字-參數(shù)分割成單獨的鍵-值對,#?所以我們能夠使用字典解包來創(chuàng)建模型的初始化版本。
def?sample_to_model(sample):
????kwargs?=?sample[MODEL_CHOICE][KWARGS]
????return?MODELS[sample[MODEL_CHOICE][MODEL]](**kwargs?"sample[MODEL_CHOICE][MODEL]")
#?定義hyperopt的目標(biāo)函數(shù)。我們將使用?`functools.partial`?修復(fù)`dataset`, `features`, 和?`target`?參數(shù)。
#?來創(chuàng)建這個函數(shù)的那個版本,?并將其作為參數(shù)提供給?`fmin`
def?objective(sample,?dataset_df,?features,?target):
????model?=?sample_to_model(sample)
????rng?=?check_random_state(0)
#?處理隨機洗牌時創(chuàng)建折疊。在現(xiàn)實中,
#?我們可能需要比上述生成的固定“RandomState”實例更好的策略來管理隨機性。
????cv?=?KFold(n_splits=10,?random_state=rng,?shuffle=True)
#?計算每一次的平均均方誤差。由于`n_splits`?是10,`mse`?將是一個大小為10的數(shù)組,
#?每個元素表示一次折疊的平均平均平方誤差。
????mse?=?cross_val_score(
????????model,
????????dataset_df.loc[:,?features],
????????dataset_df.loc[:,?target],
????????scoring=mse_scorer,
????????cv=cv,
????)
????#?返回所有折疊的均方誤差的平均值。
????return?{LOSS:?np.mean(mse),?STATUS:?STATUS_OK}
運行超參數(shù)優(yōu)化
我們將通過調(diào)用fmin函數(shù)運行一千次試驗的超參數(shù)優(yōu)化。重要的是,我們將提供一個Trials對象的實例,hyperopt 將在其中記錄超參數(shù)優(yōu)化的每次迭代的超參數(shù)設(shè)置。我們將從這個Trials實例中提取可視化數(shù)據(jù)。運行以下代碼執(zhí)行超參數(shù)優(yōu)化:
#?我們自定義的目標(biāo)函數(shù)是通用的數(shù)據(jù)集,
#?我們需要使用`partial`?從`functools`?模塊來"fix"這個`dataset_df`,?`features`,?和?`target`?的參數(shù)值,
#?希望在這個例子中,我們有一個目標(biāo)函數(shù)只接受一個參數(shù)假設(shè)的“hyperopt”界面。
boston_objective?=?partial(
????objective,?dataset_df=boston_dataset_df,?features=features,?target=MEDIAN_HOME_VALUE
)
#?`hyperopt`?跟蹤這個`Trials`對象的每次迭代的結(jié)果。
#?我們將從這個對象中收集用于可視化的數(shù)據(jù)。
trials?=?Trials()
rng?=?check_random_state(0)??#?reproducibility!
#?`fmin`搜索“minimize”我們的對象的超參數(shù),均方誤差,并返回超參數(shù)的“best”集。
best?=?fmin(boston_objective,?space,?tpe.suggest,?1000,?trials=trials,?rstate=rng)
超參數(shù)優(yōu)化可視化
Hyperopt 記錄在超參數(shù)優(yōu)化期間嘗試的超參數(shù)設(shè)置的歷史記錄在我們作為參數(shù)提供給調(diào)用 fmin 的 Trials 對象的實例中。優(yōu)化完成后,我們可以檢查trials變量以查看 hyperopt 為前五個試驗選擇了哪些設(shè)置,如下所示:
pprint([t?for?t?in?trials][:5])[{'book_time': datetime.datetime(2020, 11, 4, 0, 51, 42, 199000),
'exp_key': None,
'misc': {'cmd': ('domain_attachment', 'FMinIter_Domain'),
'idxs': {'gradient_boosting_regressor__learning_rate': [],
'gradient_boosting_regressor__max_depth': [],
'gradient_boosting_regressor__n_estimators': [],
'model_choice': [0],
'random_forest_regressor__max_depth': [0],
'random_forest_regressor__n_estimators': [0]},
'tid': 0,
'vals': {'gradient_boosting_regressor__learning_rate': [],
'gradient_boosting_regressor__max_depth': [],
'gradient_boosting_regressor__n_estimators': [],
'model_choice': [0],
'random_forest_regressor__max_depth': [5.0],
'random_forest_regressor__n_estimators': [90.0]},
'workdir': None},
'owner': None,
'refresh_time': datetime.datetime(2020, 11, 4, 0, 51, 46, 83000),
'result': {'loss': 16.359897953574603, 'status': 'ok'},
'spec': None,
'state': 2,
'tid': 0,
'version': 0},
{'book_time': datetime.datetime(2020, 11, 4, 0, 51, 46, 92000),
'exp_key': None,
'misc': {'cmd': ('domain_attachment', 'FMinIter_Domain'),
'idxs': {'gradient_boosting_regressor__learning_rate': [1],
'gradient_boosting_regressor__max_depth': [1],
'gradient_boosting_regressor__n_estimators': [1],
'model_choice': [1],
'random_forest_regressor__max_depth': [],
'random_forest_regressor__n_estimators': []},
'tid': 1,
'vals': {'gradient_boosting_regressor__learning_rate': [0.03819110609989756],
'gradient_boosting_regressor__max_depth': [8.0],
'gradient_boosting_regressor__n_estimators': [137.0],
'model_choice': [1],
'random_forest_regressor__max_depth': [],
'random_forest_regressor__n_estimators': []},
'workdir': None},
'owner': None,
'refresh_time': datetime.datetime(2020, 11, 4, 0, 51, 52, 70000),
'result': {'loss': 18.045981512632412, 'status': 'ok'},
'spec': None,
'state': 2,
'tid': 1,
'version': 0},
{'book_time': datetime.datetime(2020, 11, 4, 0, 51, 52, 81000),
'exp_key': None,
'misc': {'cmd': ('domain_attachment', 'FMinIter_Domain'),
'idxs': {'gradient_boosting_regressor__learning_rate': [2],
'gradient_boosting_regressor__max_depth': [2],
'gradient_boosting_regressor__n_estimators': [2],
'model_choice': [2],
'random_forest_regressor__max_depth': [],
'random_forest_regressor__n_estimators': []},
'tid': 2,
'vals': {'gradient_boosting_regressor__learning_rate': [0.08587985607913044],
'gradient_boosting_regressor__max_depth': [12.0],
'gradient_boosting_regressor__n_estimators': [95.0],
'model_choice': [1],
'random_forest_regressor__max_depth': [],
'random_forest_regressor__n_estimators': []},
'workdir': None},
'owner': None,
'refresh_time': datetime.datetime(2020, 11, 4, 0, 51, 57, 519000),
'result': {'loss': 21.235091223167437, 'status': 'ok'},
'spec': None,
'state': 2,
'tid': 2,
'version': 0},
{'book_time': datetime.datetime(2020, 11, 4, 0, 51, 57, 528000),
'exp_key': None,
'misc': {'cmd': ('domain_attachment', 'FMinIter_Domain'),
'idxs': {'gradient_boosting_regressor__learning_rate': [],
'gradient_boosting_regressor__max_depth': [],
'gradient_boosting_regressor__n_estimators': [],
'model_choice': [3],
'random_forest_regressor__max_depth': [3],
'random_forest_regressor__n_estimators': [3]},
'tid': 3,
'vals': {'gradient_boosting_regressor__learning_rate': [],
'gradient_boosting_regressor__max_depth': [],
'gradient_boosting_regressor__n_estimators': [],
'model_choice': [0],
'random_forest_regressor__max_depth': [2.0],
'random_forest_regressor__n_estimators': [93.0]},
'workdir': None},
'owner': None,
'refresh_time': datetime.datetime(2020, 11, 4, 0, 52, 0, 661000),
'result': {'loss': 23.582397665666413, 'status': 'ok'},
'spec': None,
'state': 2,
'tid': 3,
'version': 0},
{'book_time': datetime.datetime(2020, 11, 4, 0, 52, 0, 670000),
'exp_key': None,
'misc': {'cmd': ('domain_attachment', 'FMinIter_Domain'),
'idxs': {'gradient_boosting_regressor__learning_rate': [4],
'gradient_boosting_regressor__max_depth': [4],
'gradient_boosting_regressor__n_estimators': [4],
'model_choice': [4],
'random_forest_regressor__max_depth': [],
'random_forest_regressor__n_estimators': []},
'tid': 4,
'vals': {'gradient_boosting_regressor__learning_rate': [0.0638511443414372],
'gradient_boosting_regressor__max_depth': [5.0],
'gradient_boosting_regressor__n_estimators': [72.0],
'model_choice': [1],
'random_forest_regressor__max_depth': [],
'random_forest_regressor__n_estimators': []},
'workdir': None},
'owner': None,
'refresh_time': datetime.datetime(2020, 11, 4, 0, 52, 2, 875000),
'result': {'loss': 15.253327611719737, 'status': 'ok'},
'spec': None,
'state': 2,
'tid': 4,
'version': 0}]上下滑動查看更多
如你所見,“trials”對象本質(zhì)上是一個字典列表,其中每個字典都包含有關(guān)超參數(shù)優(yōu)化的一次迭代的詳細數(shù)據(jù)。這不是一種特別容易操作的格式,因此我們將數(shù)據(jù)的相關(guān)位轉(zhuǎn)換為“Pandas”數(shù)據(jù)幀,其中數(shù)據(jù)幀的每一行都包含一次試驗的信息:
#?這是一個簡單的輔助函數(shù),當(dāng)一個特定的超參數(shù)與一個特定的試驗無關(guān)時,
#?允許我們填充`np.nan`。
def?unpack(x):
????if?x:
????????return?x[0]
????return?np.nan
#?我們將首先將每個試驗轉(zhuǎn)換為一個系列,然后將這些系列堆疊在一起作為一個數(shù)據(jù)框架。
trials_df?=?pd.DataFrame([pd.Series(t["misc"]["vals"]).apply(unpack)?for?t?in?trials])
#?然后,我們將添加其他相關(guān)的信息到正確的行,并執(zhí)行一些方便的映射
trials_df["loss"]?=?[t["result"]["loss"]?for?t?in?trials]
trials_df["trial_number"]?=?trials_df.index
trials_df[MODEL_CHOICE]?=?trials_df[MODEL_CHOICE].apply(
????lambda?x:?RANDOM_FOREST_REGRESSOR?if?x?==?0?else?GRADIENT_BOOSTING_REGRESSOR
我們再看一下這種新格式的前五個試驗:

這比我們之前的字典列表更易于管理。
使用 Plotly Express 繪制試驗數(shù)量與損失
可視化試驗迭代的一種有用方法是繪制試驗次數(shù)與損失的關(guān)系圖,以查看超參數(shù)優(yōu)化是否如我們預(yù)期的那樣隨時間收斂。使用 Plotly 的高級Express[3]界面使這變得容易;我們只需在我們的數(shù)據(jù)幀上調(diào)用scatter方法并指出我們想要使用哪些列作為 x 和 y 值:
#?px是“express”的別名,它是按照導(dǎo)入“express”的約定通過運行
#?“from plotly import express as px”創(chuàng)建的。
fig?=?px.scatter(trials_df,?x="trial_number",?y="loss")
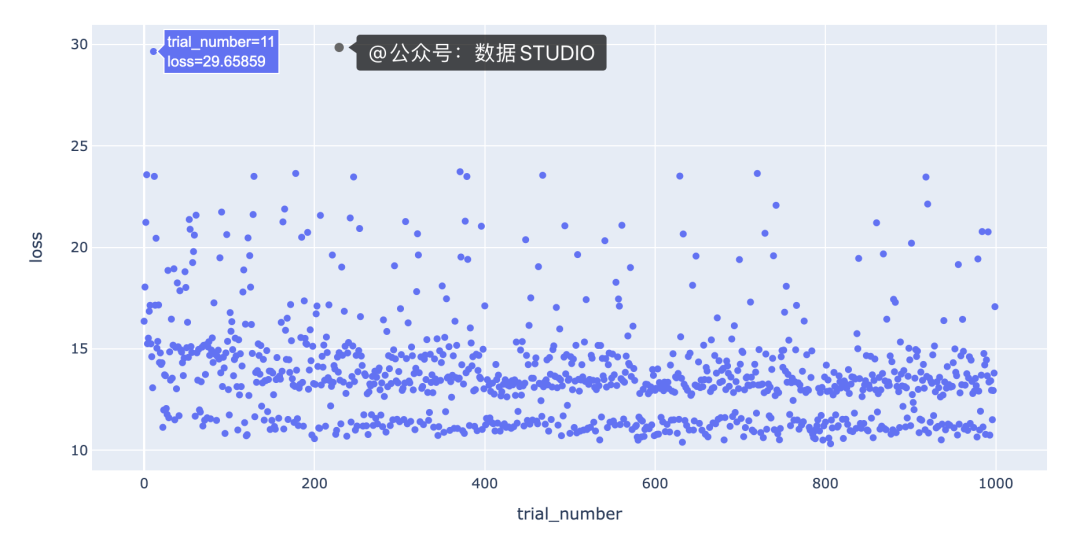
該圖的一個有趣特征是,底行具有“損失”值在 10 到 12 之間的點與其余點之間存在明顯的分隔。我們需要更多信息來了解導(dǎo)致這種分離的原因。一種假設(shè)是分離是由不同的模型類型引起的;例如,底行的點可能都是梯度提升回歸模型,其余的點可能都是隨機森林回歸模型。
我們對每種模型類型的點進行不同的著色,以查看是否是這種情況,方法是color在方法調(diào)用中添加一個參數(shù),scatter如下所示:
fig?=?px.scatter(trials_df,?
?????????????????x="trial_number",?
?????????????????y="loss",
?????????????????color=MODEL_CHOICE)
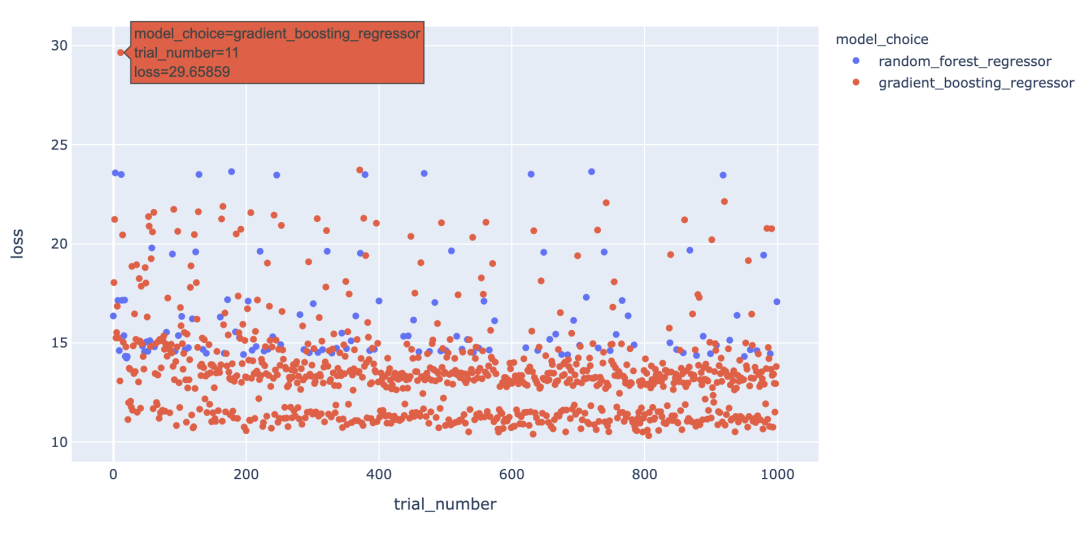
有趣的是,我們看到模型類型并不能完全解釋底行點與其余點之間的差距,因為梯度提升回歸模型也出現(xiàn)在其余點中。
我們可以通過創(chuàng)建交互式可視化來為可視化中的信息添加更多深度,這樣當(dāng)我們將鼠標(biāo)懸停在每個點上時,我們可以看到導(dǎo)致該點丟失的一組超參數(shù)。起初,看起來我們應(yīng)該能夠通過簡單地為hover_datascatter 方法的參數(shù)包含一個值來實現(xiàn)這一點。但是,由于我們只想為每個點包含與每種模型類型相關(guān)的超參數(shù),因此我們需要在update_trace調(diào)用 scatter 之后調(diào)用該方法以添加懸停數(shù)據(jù),因為這允許我們過濾為每個點顯示哪些超參數(shù)觀點。看起來是這樣的
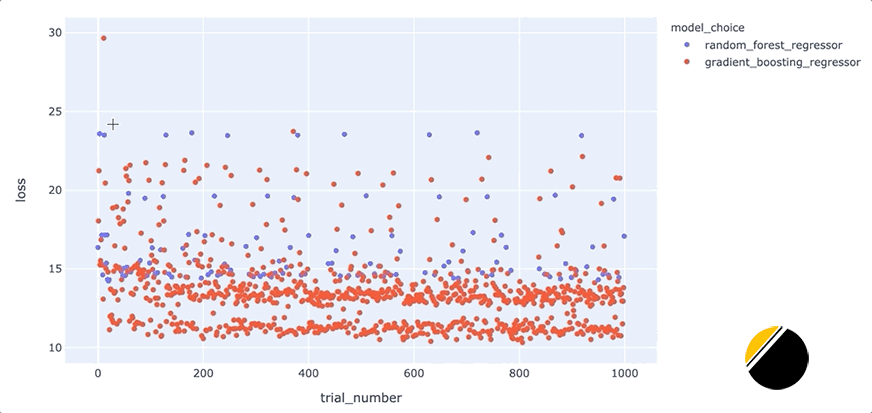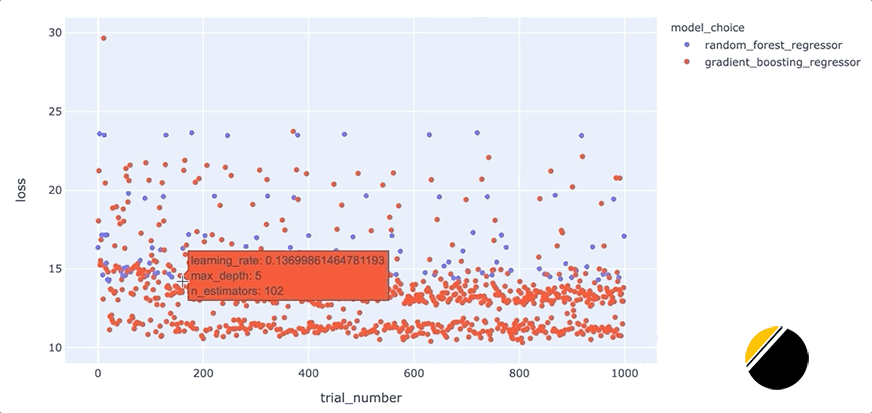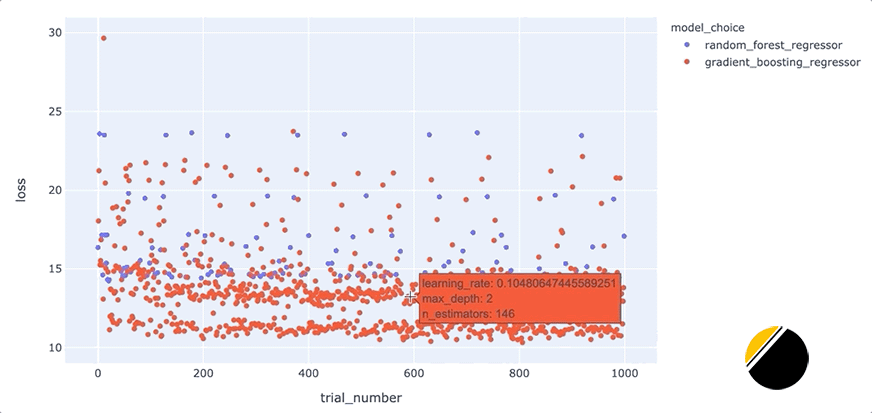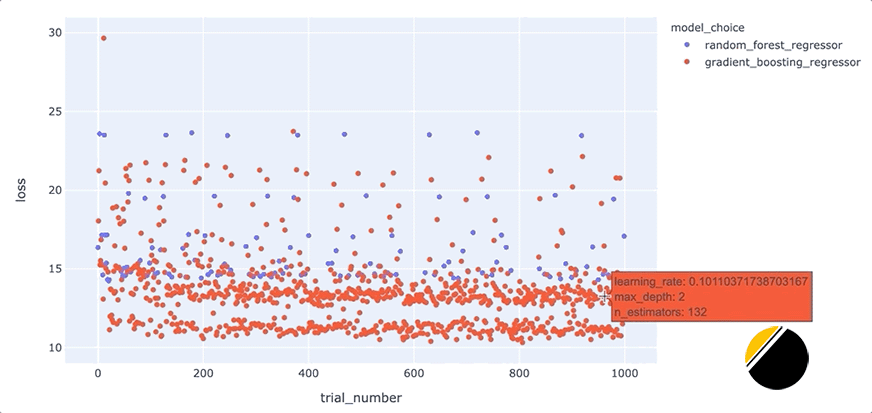
我們可以通過這些額外的細節(jié)來說明什么?將鼠標(biāo)懸停在與底行中最佳模型相對應(yīng)的點上,可以發(fā)現(xiàn)max_depth每個點的參數(shù)設(shè)置為3。
此外,將鼠標(biāo)懸停在該行之外的點上會顯示參數(shù)max_depth設(shè)置為3以外的值,例如2、4或5。這表明在我們的數(shù)據(jù)集中,參數(shù)max_depth可能有一些特殊之處。例如,這可能表明模型性能主要由三個特征驅(qū)動。我們將希望進一步研究為什么max_depth=3對我們的數(shù)據(jù)集如此有效,并且我們可能希望為我們構(gòu)建和部署的最終模型將max_depth設(shè)置為3。
在特征之間創(chuàng)建等高線圖
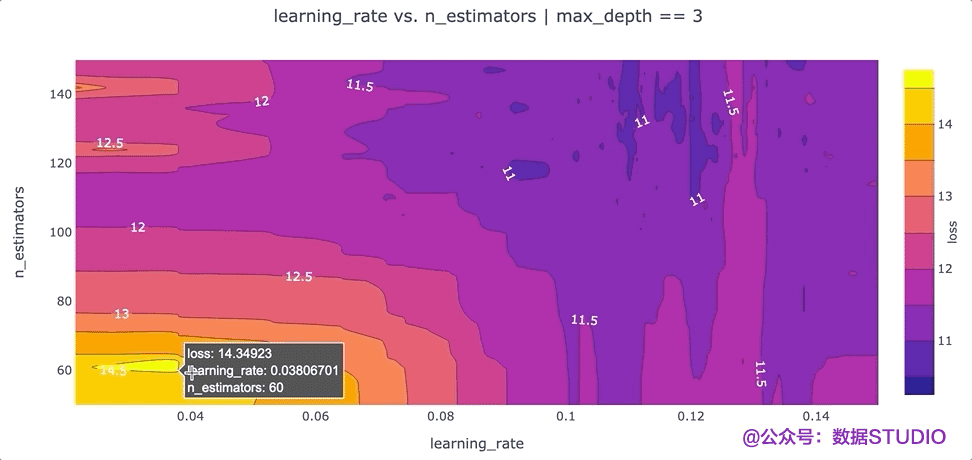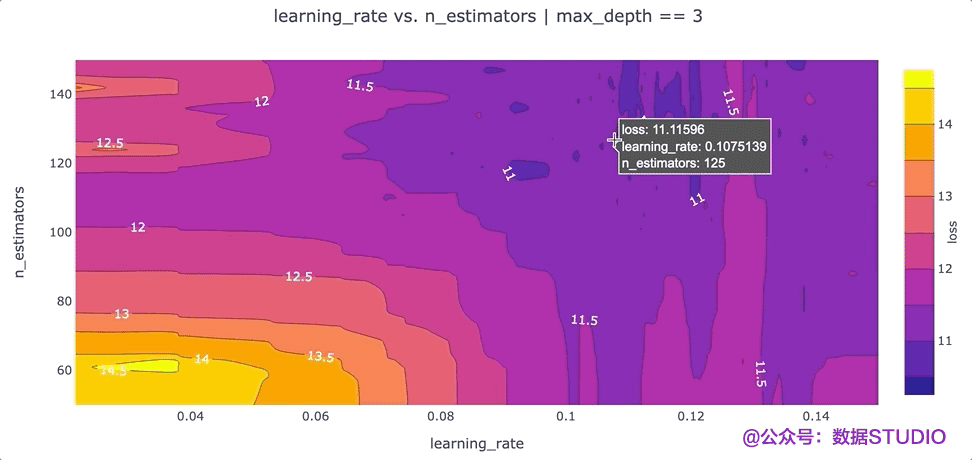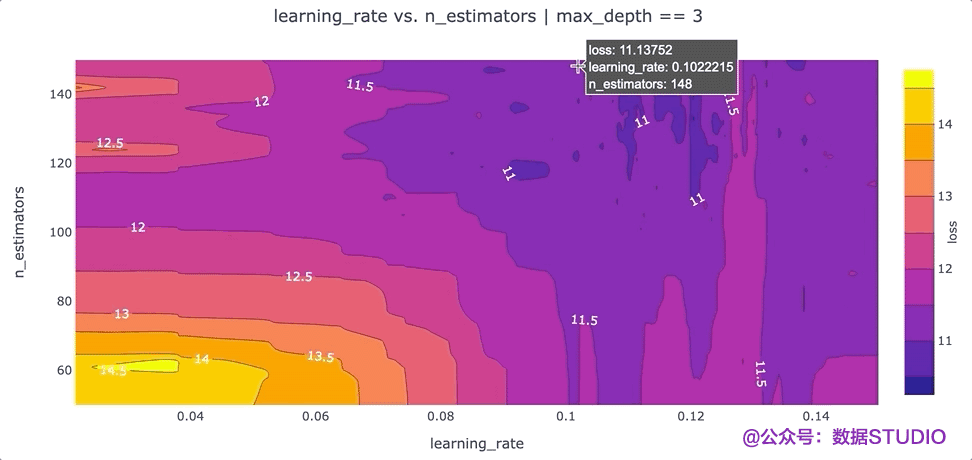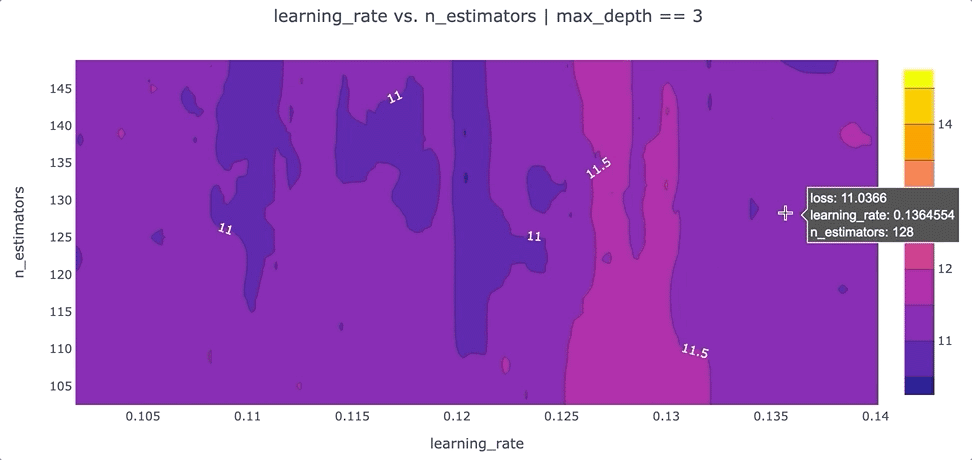
另一個可以提高我們對超參數(shù)設(shè)置直覺的可視化是根據(jù)超參數(shù)的“損失”值的等高線圖。等高線圖特別強大,因為它們揭示了不同超參數(shù)設(shè)置之間的交互如何影響損失。通常,我們希望為每對超參數(shù)生成一個單獨的等高線圖。在這種情況下,為了簡單起見,我們max_depth將超參數(shù)的值固定為 3,并繪制該數(shù)據(jù)切片的learning_ratevs.n_estimatorsloss 等值線。我們可以通過運行以下命令使用 Plotly 創(chuàng)建這個等高線圖:
#?plotly?express不支持輪廓圖,
#?所以我們將使用'graph_objects'來代替。
#?`go.Contour`自動為我們的損失插入“z”值。
fig?=?go.Figure(
????data=go.Contour(
????????z=trials_df.loc[max_depth_filter,?"loss"],
????????x=trials_df.loc[max_depth_filter,?"gradient_boosting_regressor__learning_rate"],
????????y=trials_df.loc[max_depth_filter,?"gradient_boosting_regressor__n_estimators"],
????????contours=dict(
????????????showlabels=True,??#?顯示輪廓上的標(biāo)簽
????????????labelfont=dict(size=12,?color="white",),??
????????????#?標(biāo)簽字體屬性
????????),
????????colorbar=dict(title="loss",?titleside="right",),
????????hovertemplate="loss:?%{z}
learning_rate:?%{x}
n_estimators:?%{y}
????)
)
fig.update_layout(
????xaxis_title="learning_rate",
????yaxis_title="n_estimators",
????title={
????????"text":?"learning_rate?vs.?n_estimators?|?max_depth?==?3",
????????"xanchor":?"center",
????????"yanchor":?"top",
????????"x":?0.5,
????},
)
該圖的一個要點是,我們可能希望嘗試增加最大值n_estimators超參數(shù),因為損失最低的區(qū)域出現(xiàn)在該圖的頂部。
寫在最后
在這篇文章中,我們介紹了如何將試驗對象中包含的數(shù)據(jù)轉(zhuǎn)換為 Pandas 數(shù)據(jù)框,以便我們可以輕松分析超參數(shù)設(shè)置的歷史。一旦我們在數(shù)據(jù)框中獲得了數(shù)據(jù),我們就可以輕松地創(chuàng)建可視化,讓我們更好地了解為什么一組特定的超參數(shù)設(shè)置是最好的。特別是,我們已經(jīng)證明,通過使用 Plotly 創(chuàng)建簡單的交互式可視化來增加可視化的深度,可以揭示一些非常適合我們的問題的超參數(shù)設(shè)置的有趣趨勢。此外,我們已經(jīng)展示了等高線圖對于指示我們可能想要對超參數(shù)搜索空間進行的調(diào)整很有用。
原文鏈接: https://medium.com/doma/visualizing-hyperparameter-optimization-with-hyperopt-and-plotly-states-title 來源:@公眾號:數(shù)據(jù)STUDIO
參考資料
hyperopt 文檔英文教程:https://github.com/hyperopt/hyperopt/wiki/FMin#22-a-search-space-example-scikit-learn
[2]UCI:https://gitee.com/yunduodatastudio/picture/blob/master/data/ICU.png
[3]Express:https://plotly.com/python/plotly-express/
推薦閱讀
