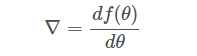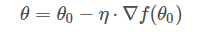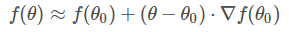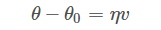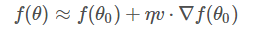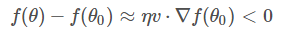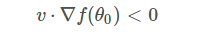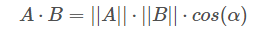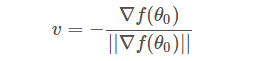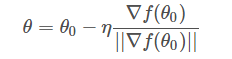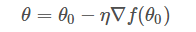梯度下降算法的公式非常簡(jiǎn)單，”沿著梯度的反方向（坡度最陡）“是我們?nèi)粘＝?jīng)驗(yàn)得到的，其本質(zhì)的原因到底是什么呢？為什么局部下降最快的方向就是梯度的負(fù)方向呢？也許很多朋友還不太清楚。沒(méi)關(guān)系，接下來(lái)我將以通俗的語(yǔ)言來(lái)詳細(xì)解釋梯度下降算法公式的數(shù)學(xué)推導(dǎo)過(guò)程。

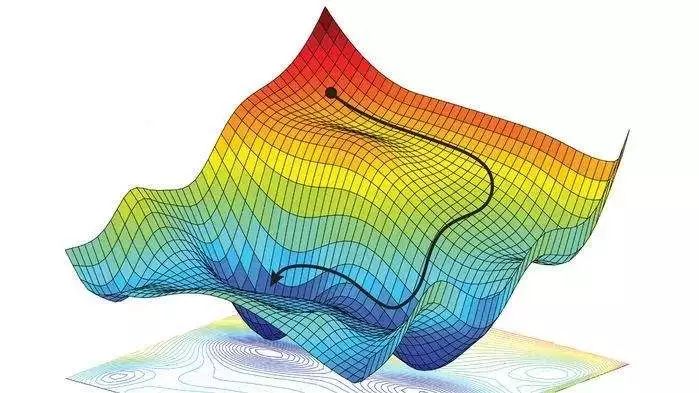
假設(shè)我們位于黃山的某個(gè)山腰處，山勢(shì)連綿不絕，不知道怎么下山。于是決定走一步算一步，也就是每次沿著當(dāng)前位置最陡峭最易下山的方向前進(jìn)一小步，然后繼續(xù)沿下一個(gè)位置最陡方向前進(jìn)一小步。這樣一步一步走下去，一直走到覺(jué)得我們已經(jīng)到了山腳。這里的下山最陡的方向就是梯度的負(fù)方向。

首先理解什么是梯度？通俗來(lái)說(shuō)，梯度就是表示某一函數(shù)在該點(diǎn)處的方向?qū)?shù)沿著該方向取得最大值，即函數(shù)在當(dāng)前位置的導(dǎo)數(shù)。

上式中，θ?是自變量，f(θ)?是關(guān)于?θ?的函數(shù)，θ?表示梯度。

如果函數(shù)?f(θ)?是凸函數(shù)，那么就可以使用梯度下降算法進(jìn)行優(yōu)化。梯度下降算法的公式我們已經(jīng)很熟悉了：

其中，θo?是自變量參數(shù)，即下山位置坐標(biāo)，η?是學(xué)習(xí)因子，即下山每次前進(jìn)的一小步（步進(jìn)長(zhǎng)度），θ?是更新后的?θo，即下山移動(dòng)一小步之后的位置。

這里需要一點(diǎn)數(shù)學(xué)基礎(chǔ)，對(duì)泰勒展開(kāi)式有些了解。簡(jiǎn)單地來(lái)說(shuō)，一階泰勒展開(kāi)式利用的就是函數(shù)的局部線性近似這個(gè)概念。我們以一階泰勒展開(kāi)式為例：

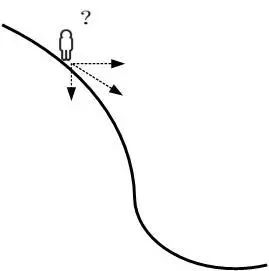
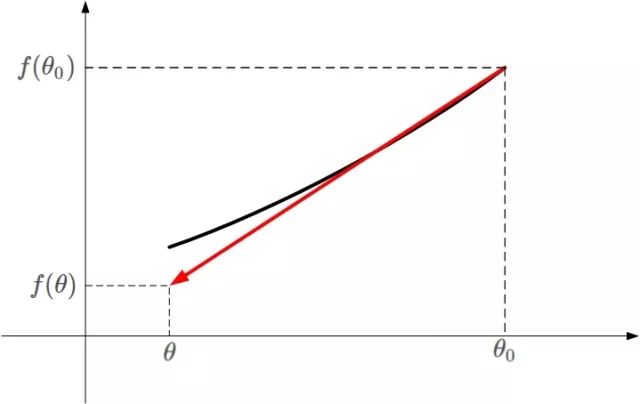
不懂上面的公式？沒(méi)有關(guān)系。我用下面這張圖來(lái)解釋。

凸函數(shù)?f(θ)?的某一小段 [θo,θ] 由上圖黑色曲線表示，可以利用線性近似的思想求出?f(θ)?的值，如上圖紅色直線。該直線的斜率等于?f(θ)?在?θo?處的導(dǎo)數(shù)。則根據(jù)直線方程，很容易得到?f(θ)?的近似表達(dá)式為：

這就是一階泰勒展開(kāi)式的推導(dǎo)過(guò)程，主要利用的數(shù)學(xué)思想就是曲線函數(shù)的線性擬合近似。

知道了一階泰勒展開(kāi)式之后，接下來(lái)就是重點(diǎn)了！我們來(lái)看一下梯度下降算法是如何推導(dǎo)的。

先寫(xiě)出一階泰勒展開(kāi)式的表達(dá)式：

其中，θ?θo?是微小矢量，它的大小就是我們之前講的步進(jìn)長(zhǎng)度?η，類比于下山過(guò)程中每次前進(jìn)的一小步，η?為標(biāo)量，而?θ?θo?的單位向量用?v?表示。則?θ?θo?可表示為：

特別需要注意的是，θ?θo?不能太大，因?yàn)樘蟮脑挘€性近似就不夠準(zhǔn)確，一階泰勒近似也不成立了。替換之后，f(θ)?的表達(dá)式為：

重點(diǎn)來(lái)了，局部下降的目的是希望每次?θ?更新，都能讓函數(shù)值?f(θ)?變小。也就是說(shuō)，上式中，我們希望?f(θ)。則有：

因?yàn)?η?為標(biāo)量，且一般設(shè)定為正值，所以可以忽略，不等式變成了：

上面這個(gè)不等式非常重要！v?和??f(θo)?都是向量，?f(θo)?是當(dāng)前位置的梯度方向，v?表示下一步前進(jìn)的單位向量，是需要我們求解的，有了它，就能根據(jù)?vθ?θo=ηv?確定?θ?值了。

想要兩個(gè)向量的乘積小于零，我們先來(lái)看一下兩個(gè)向量乘積包含哪幾種情況：

A?和?B?均為向量，α?為兩個(gè)向量之間的夾角。A?和?B?的乘積為：

||A|| 和 ||B|| 均為標(biāo)量，在 ||A|| 和 ||B|| 確定的情況下，只要 cos(α)=?1，即?A?和?B?完全反向，就能讓?A?和?B?的向量乘積最小（負(fù)最大值）。

顧名思義，當(dāng)?v?與??f(θo)?互為反向，即?v?為當(dāng)前梯度方向的負(fù)方向的時(shí)候，能讓?v??f(θo)?最大程度地小，也就保證了?v?的方向是局部下降最快的方向。

知道 v 是??f(θo)?的反方向后，可直接得到：

之所以要除以??f(θo)?的模 ||?f(θo)||，是因?yàn)?v?是單位向量。

求出最優(yōu)解?v?之后，帶入到?θ?θo=ηv?中，得：

一般地，因?yàn)?||?f(θo)|| 是標(biāo)量，可以并入到步進(jìn)因子?η?中，即簡(jiǎn)化為：

這樣，我們就推導(dǎo)得到了梯度下降算法中?θ?的更新表達(dá)式。

我們通過(guò)一階泰勒展開(kāi)式，利用線性近似和向量相乘最小化的思想搞懂了梯度下降算法的數(shù)學(xué)原理。也許你之前很熟悉梯度下降算法，但也許對(duì)它的推導(dǎo)過(guò)程并不清楚。看了本文，你是否有所收獲呢？

交流群

歡迎加入公眾號(hào)讀者群一起和同行交流，目前有SLAM、三維視覺(jué)、傳感器、自動(dòng)駕駛、計(jì)算攝影、檢測(cè)、分割、識(shí)別、醫(yī)學(xué)影像、GAN、算法競(jìng)賽等微信群（以后會(huì)逐漸細(xì)分），請(qǐng)掃描下面微信號(hào)加群，備注：”昵稱+學(xué)校/公司+研究方向“，例如：”張三?+?上海交大?+?視覺(jué)SLAM“。請(qǐng)按照格式備注，否則不予通過(guò)。添加成功后會(huì)根據(jù)研究方向邀請(qǐng)進(jìn)入相關(guān)微信群。請(qǐng)勿在群內(nèi)發(fā)送廣告，否則會(huì)請(qǐng)出群，謝謝理解~