5分鐘完全讀懂關聯(lián)規(guī)則挖掘算法
關聯(lián)規(guī)則簡介
關聯(lián)規(guī)則挖掘可以讓我們從數據集中發(fā)現(xiàn)項與項之間的關系,它在我們的生活中有很多應用場景,“購物籃分析”就是一個常見的場景,這個場景可以從消費者交易記錄中發(fā)掘商品與商品之間的關聯(lián)關系,進而通過商品捆綁銷售或者相關推薦的方式帶來更多的銷售量。
搞懂關聯(lián)規(guī)則中的幾個重要概念:支持度、置信度、提升度
Apriori 算法的工作原理
在實際工作中,我們該如何進行關聯(lián)規(guī)則挖掘
關聯(lián)規(guī)則中重要的概念
我舉一個超市購物的例子,下面是幾名客戶購買的商品列表:
| 訂單編號 | 購買商品 |
|---|---|
| 1 | 牛奶、面包、尿布 |
| 2 | 可樂、面包、尿布、啤酒 |
| 3 | 牛奶、尿布、啤酒、雞蛋 |
| 4 | 面包、牛奶、尿布、啤酒 |
| 5 | 面包、牛奶、尿布、可樂 |
支持度
支持度是個百分比,它指的是某個商品組合出現(xiàn)的次數與總次數之間的比例。支持度越高,代表這個組合出現(xiàn)的頻率越大。
我們看啤酒出現(xiàn)了3次,那么5筆訂單中啤酒的支持度是3/5=0.6。同理,尿布出現(xiàn)了5次,那么尿布的支持度是5/5=1。尿布和啤酒同時出現(xiàn)的支持度是3/6=0.6。
置信度
它指的就是當你購買了商品 A,會有多大的概率購買商品 B。
我們可以看上面的商品,購買尿布的同時又購買啤酒的訂單數是3,購買啤酒的訂單數是3,那么(尿布->啤酒)置信度= 3/3=1。
再看購買了啤酒同時購買尿布的訂單數是3,購買尿布的訂單數是5,那么(啤酒->尿布)置信度=3/5=0.6。
提升度
提升度代表的是“商品 A 的出現(xiàn),對商品 B 的出現(xiàn)概率提升的”程度。所以我們在做商品推薦的時候,重點考慮的是提升度。
我們來看提升度公式: 那么我們來計算下尿布對啤酒的提升度是多少:?
那么我們來計算下尿布對啤酒的提升度是多少:?



怎么解讀1.67這個數值呢?
提升度 (A→B)>1:代表有提升
提升度 (A→B)=1:代表有沒有提升,也沒有下降
提升度 (A→B)<1:代表有下降。
其實看上面提升度的公式,我們就可以理解,也就是AB同時出現(xiàn)的次數越多,單獨出現(xiàn)B的次數越少,那么支持度也就越大也就是B的出現(xiàn)總是伴隨著A的出現(xiàn),那么A對B出現(xiàn)的概率就越有提升!
Apriori 的工作原理
我們一起來看下經典的關聯(lián)規(guī)則 Apriori 算法是如何工作的。
Apriori 算法其實就是查找頻繁項集 (frequent itemset) 的過程,所以我們需要先了解是頻繁項集。
頻繁項集就是支持度大于等于最小支持度閾值的項集,所以小于最小值支持度的項目就是非頻繁項集,而大于等于最小支持度的項集就是頻繁項集。
下面我們來舉個栗子:
假設我隨機指定最小支持度是0.2。首先,我們先計算單個商品的支持度:
| 購買商品 | 支持度 |
|---|---|
| 牛奶 | 4/5 |
| 面包 | 4/5 |
| 尿布 | 5/5 |
| 可樂 | 2/5 |
| 啤酒 | 3/5 |
| 雞蛋 | 1/5 |
因為最小支持度是 0.2,所以你能看到商品 雞蛋 是不符合最小支持度的,不屬于頻繁項集,于是經過篩選商品的頻繁項集如下:
| 購買商品 | 支持度 |
|---|---|
| 牛奶 | 4/5 |
| 面包 | 4/5 |
| 尿布 | 5/5 |
| 可樂 | 2/5 |
| 啤酒 | 3/5 |
在這個基礎上,我們將商品兩兩組合,得到兩個商品的支持度:
| 購買商品 | 支持度 |
|---|---|
| 牛奶、面包 | 3/5 |
| 牛奶、尿布 | 4/5 |
| 牛奶、可樂 | 1/5 |
| 牛奶、啤酒 | 2/5 |
| 面包、尿布 | 4/5 |
| 面包、可樂 | 2/5 |
| 面包、啤酒 | 2/5 |
| 尿布、可樂 | 2/5 |
| 尿布、啤酒 | 3/5 |
| 可樂、啤酒 | 1/5 |
篩選大于最小支持度(0.2)的數據后
| 購買商品 | 支持度 |
|---|---|
| 牛奶、面包 | 3/5 |
| 牛奶、尿布 | 4/5 |
| 牛奶、啤酒 | 2/5 |
| 面包、尿布 | 4/5 |
| 面包、可樂 | 2/5 |
| 面包、啤酒 | 2/5 |
| 尿布、可樂 | 2/5 |
| 尿布、啤酒 | 3/5 |
在這個基礎上,我們再將商品三個組合,得到三個商品的支持度:
| 購買商品 | 支持度 |
|---|---|
| 牛奶、面包、尿布 | 3/5 |
| 牛奶、面包、可樂 | 1/5 |
| 牛奶、面包、啤酒 | 1/5 |
| 面包、尿布、可樂 | 1/5 |
| 面包、尿布、啤酒 | 2/5 |
| 尿布、可樂、啤酒 | 1/5 |
篩選大于最小支持度(0.2)的數據后
| 購買商品 | 支持度 |
|---|---|
| 牛奶、面包、尿布 | 3/5 |
| 面包、尿布、啤酒 | 2/5 |
在這個基礎上,我們將商品四個組合,得到四個商品的支持度:
| 購買商品 | 支持度 |
|---|---|
| 牛奶、面包、尿布、可樂 | 1/5 |
| 牛奶、面包、尿布、啤酒 | 1/5 |
| 面包、尿布、可樂、啤酒 | 1/5 |
再次篩選大于最小支持度(0.2)數據的話,就全刪除了,那么,此時算法結束,上一次的結果就是我們要找的頻繁項,也就是{牛奶、面包、尿布}、{面包、尿布、啤酒}。
我們來總結一下上述Apriori算法過程:
K=1,計算 K 項集的支持度
篩選掉小于最小支持度的項集
如果項集為空,則對應 K-1 項集的結果為最終結果
否則 K=K+1,重復 1-3 步
我們可以看到 Apriori 在計算的過程中有以下幾個缺點:
可能產生大量的候選集。因為采用排列組合的方式,把可能的項集都組合出來了
每次計算都需要重新掃描數據集,來計算每個項集的支持度
這就好比我們數據庫中的“全表掃描”查詢一樣,非常浪費IO和時間。在數據庫中我們都知道使用索引來快速檢索數據,那Apriori 能優(yōu)化嗎?
Apriori 的改進算法:FP-Growth 算法
FP-growth算法是基于Apriori原理的,通過將數據集存儲在FP樹上發(fā)現(xiàn)頻繁項集,但不能發(fā)現(xiàn)數據之間的關聯(lián)規(guī)則。FP-growth算法只需要對數據庫進行兩次掃描,而Apriori算法在求每個潛在的頻繁項集時都需要掃描一次數據集,所以說Apriori算法是高效的。其中算法發(fā)現(xiàn)頻繁項集的過程是:(1)構建FP樹;(2)從FP樹中挖掘頻繁項集。
創(chuàng)建項頭表
概念知識不在這湊字數了,我們直接來干貨!假設我們從以下數據中來挖掘頻繁項。
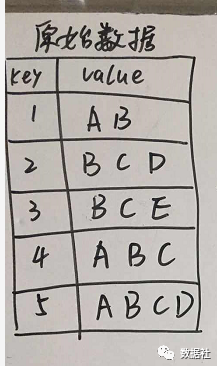
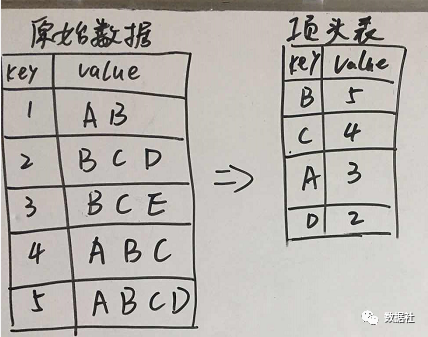
首先創(chuàng)建,項頭表,這一步的流程是先掃描一遍數據集,對于滿足最小支持度的單個項按照支持度從高到低進行排序,這個過程中刪除了不滿足最小支持度的項(假設最小支持度是0.2)。
構建FP樹
整個流程是需要再次掃描數據集,對于每一條數據,按照支持度從高到低的順序進行創(chuàng)建節(jié)點(也就是第一步中項頭表中的排序結果),節(jié)點如果存在就將計數 count+1,如果不存在就進行創(chuàng)建。同時在創(chuàng)建的過程中,需要更新項頭表的鏈表。
先把原始數據按照支持度排序,那么原始數據變化如下:
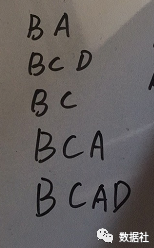
下面我們把以上每行數據,按照順序插入到FP樹中,注意FP樹的根節(jié)點記為 NULL 節(jié)點。

接下來插入第二行數據,由于第二行數據第一個數據也是B,和已有的樹結構重合,那么我們保持原來樹結構中的B位置不變,同時計數加1,C、D是新增數據,那么就會有新的樹分叉,結果如下圖:

以此類推,讀取下面的三行數據到FP樹中

最后生成的FP數如下:

根據FP數挖掘頻繁項
我們終于把FP樹建立好了,那么如何去看這顆樹呢?得到 FP 樹后,需要對每一個頻繁項,逐個挖掘頻繁項集。具體過程為:首先獲得頻繁項的前綴路徑,然后將前綴路徑作為新的數據集,以此構建前綴路徑的條件 FP 樹。然后對條件 FP 樹中的每個頻繁項,獲得前綴路徑并以此構建新的條件 FP 樹。不斷迭代,直到條件 FP 樹中只包含一個頻繁項為止(反正我第一次看完這句話是沒理解)。
FP樹是從下往上看了,也就是根據子節(jié)點找父節(jié)點,接下來還是來圖解~
首先,我們看包含A的頻繁項:
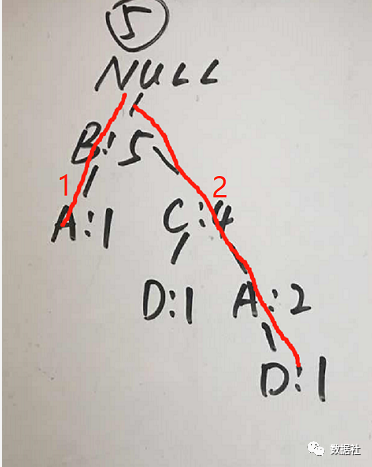
我們可以看到包含A的樹有兩個,我們先看樹2,可以得到路徑{B:2,C:2},此處的2是根據A出現(xiàn)的次數定的。接著我們創(chuàng)建FP樹,具體的創(chuàng)建過程和上面創(chuàng)建 FP 樹的過程一樣,如下圖:

注意此時頭指針表中包含兩個元素,所以對每個元素,需要獲得前綴路徑,并將前綴路徑創(chuàng)建成條件 FP 樹,直到條件 FP 樹中只包含一個元素時返回。
對元素 B,獲得前綴路徑為{},則頻繁項集返回{A:2,B:2};
對元素 C,獲得前綴路徑{B:2},則將前綴路徑創(chuàng)建成條件 FP 樹,如下圖 ?所示。
注意此時條件 FP 樹中只包含一個元素,故返回頻繁項集{A:2,C:2,B:2}。由于元素 C 也是頻繁項,所以{A:2,C:2}也是頻繁項集。
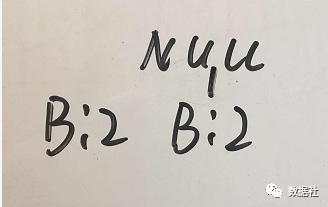
再加上{A:2}本身就是頻繁項集,所以 A 對應的頻繁項集有:{A:2},{A:2,C:2} ,{A:2,B:2},{A:2,C:2,B:2}。
同理,我們來看樹1,樹1比較簡單,就一個路徑{B:1},根據上述方法我們得到此分支頻繁項為{A:1,B:1},{A:1}。
綜上,我們可以看到兩個分支都包含頻繁項{A,B},{A}的,此時我們進行合并兩個分支,得到包含A的頻繁項:{A:3},{A:3,B:3},{A:2,C:2}?,{A:2,C:2,B:2},我們用出現(xiàn)的次數轉換下,即?(A,): 3, (A, B): 3, (A, C): 2, (A, B, C): 2。
同理,按照上述方法,我們可以依次找到包含B的頻繁項是(D): 2, (C, D): 2, (B, D): 2, (B, C, D): 2, ?(C): 4, (B, C): 4, (B): 5。
實踐總結
經典的算法,很多大神已經實現(xiàn),我們直接拿來用就行了,比如上面的FP-GROWTH算法,介紹一款專門的包pyfpgrowth。
代碼:
import pyfpgrowth as fp
itemsets = [['A','B'], ['B','C','D'],['B','C'],['A','B','C'],['A','B','C','D']]
# 頻數刪選 頻數大于2
patterns = fp.find_frequent_patterns(itemsets, 2)
print(patterns)
{('D',): 2, ('C', 'D'): 2, ('B', 'D'): 2, ('B', 'C', 'D'): 2, ('A',): 3, ('A', 'B'): 3, ('A', 'C'): 2, ('A', 'B', 'C'): 2, ('C',): 4, ('B', 'C'): 4, ('B',): 5}很對人會問算法原理看著很費勁,直接兩行代碼搞定。我們還看原理干嘛,直接寫(抄)代碼不就行了。我舉個例子哈,記得上小學3年級的時候,有一次數學考試,老師出了一道附加題:
附加題(10分):求1+2+3+…+99+100的和。提示:參考梯形面積計算公式。
當然,對于一個初中生,這道題很好解答,但對于一個小學三年級的學生來說還是比較難的。但是,我知道梯形的計算公式:
梯形面積?=?(上底+下底)×高÷2所以,就按照這個計算了
1+2+3+…+99+100?=?(1?+?100)x100÷2其實,算法原理也是一樣,我們了解后,可以舉一反三的使用,并不一定總是在一個場景下使用的。
長按掃碼添加“Python小助手”
▼點擊成為社區(qū)會員? ?喜歡就點個在看吧
